层流火焰概念特点

层流燃烧课题
层流燃烧是一种能够实现高效节能、减少污染的燃烧方式，被广泛应用于工业、能源等领域。

其主要特点是将燃料和空气分层注入燃烧室，使燃料在较低温度下燃烧，减少了污染物的生成和能量的浪费。

层流燃烧课题主要包括以下内容：
1. 层流燃烧的基本原理及机理：研究层流燃烧流场的特性、燃料燃烧机理以及
污染物的生成机理等基本问题，为层流燃烧的优化设计提供理论基础。

2. 层流燃烧的优化设计：通过数值模拟和实验研究，探究层流燃烧在不同工况
下的最优化设计，包括燃料和空气的注入方式、燃烧室结构、燃料种类等方面的优化。

3. 层流燃烧的应用及推广：将层流燃烧技术应用于实际生产中，包括工业锅炉、发电厂、汽车等领域，在实践中不断完善和优化技术，推广层流燃烧技术的应用和推广。

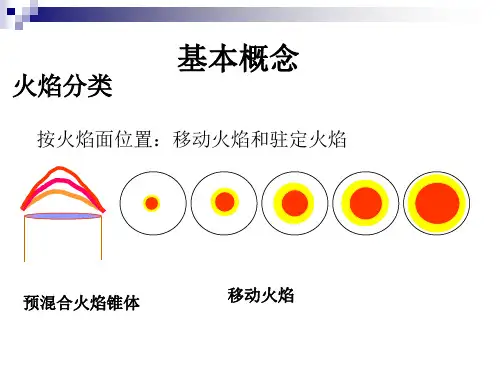
层流火焰概念层流火焰概念层流火焰是指在燃烧室中形成的一种稳定的、纵向分层的火焰结构。

它是工业燃烧过程中常见的一种火焰形态，具有高效、稳定和低排放等优点，广泛应用于工业生产中。

一、层流火焰的定义和特点1.1 定义层流火焰是指在燃烧室中形成的一种稳定的、纵向分层的火焰结构。

它通常由多个较薄且相对独立的气体层组成，每个气体层内部具有相同的温度和组成，并且相邻两个气体层之间存在明显的温度和组成梯度。

1.2 特点（1）高效：由于每个气体层内部具有相同的温度和组成，可以有效地控制燃料和氧气之间的混合程度，使得燃料能够充分地与氧气反应，从而提高燃烧效率。

（2）稳定：由于每个气体层都是相对独立的，不会相互干扰或干扰外部环境，因此层流火焰具有较高的稳定性，不易受到外界因素的影响。

（3）低排放：由于燃料和氧气之间的混合程度受到有效控制，可以使得燃烧产生的废气排放量降低，从而减少对环境的污染。

二、层流火焰的形成机理2.1 燃料和氧气混合在燃烧室中，燃料和氧气通过喷嘴或其他方式进入，并在一定条件下混合。

由于不同层次之间存在温度和组成梯度，使得混合程度不同。

通常情况下，在较高温度和较高浓度的区域，混合程度较好；而在较低温度和较低浓度的区域，则混合程度相对较差。

2.2 燃烧反应当燃料和氧气混合到一定程度时，就会发生燃烧反应。

在反应过程中，产生大量的能量释放，并且会改变温度、压力和组成等参数。

由于不同层次之间存在温度和组成梯度，使得燃烧反应发生的位置和强度不同。

通常情况下，在较高温度和较高浓度的区域，燃烧反应比较强烈；而在较低温度和较低浓度的区域，则反应相对较弱。

2.3 火焰传播随着燃料和氧气的不断混合和反应，火焰开始在燃烧室内传播。

由于不同层次之间存在温度和组成梯度，使得火焰传播速度不同。

通常情况下，在较高温度和较高浓度的区域，火焰传播速度比较快；而在较低温度和较低浓度的区域，则传播速度相对较慢。

三、层流火焰的应用领域层流火焰具有高效、稳定和低排放等优点，广泛应用于工业生产中。

层流火焰与湍流火焰的结构一、层流火焰分析层流火焰速度和火焰结构一维层流火焰在预混燃料-氧化剂混合物中传播是最简单的燃烧现象之一，在此火焰中，化学动力学以及能量和组分扩散输运起重要作用。

通过守恒方程和状态方程可以导出Rankine-Hugoniot 曲线。

该曲线把在一维层流预混火焰中未燃气和已燃气状态联系起来。

已燃气体位于Rankine-Hugoniot 曲线下分支（缓燃），并相应于未燃气体状态Rayleigh 线与具有适当反应热的Rankine-Hugoniot 曲线交点L，如图1-2中所示。

图1 层流预混火焰坐标系图 2 一维燃烧波的Rankine-Hugoniot 曲线和Rayleigh 线Rayleigh 线的斜率与相对于未燃气体的波的传播速度，即层流火焰速度有关。

/ ( / )2 ( )2 u u dP dv = −m& A = −ρu(= ) = u u u S 层流火焰速度= (1/ ) (dP / dv) u −ρ由于缓燃Rayleigh 线斜率比爆震Rayleigh 线斜率小得多，所以缓燃速度比爆震速度小得多。

虽然守恒方程和状态方程提供了缓燃的未燃气体和已燃状态之间的关系，但不能唯一确定层流火焰速度Su 。

为了确定Su ，必须将守恒方程通过缓燃波积分。

由于 96方程是非线性耦合微分方程，其准确解只有通过数值积分才能获得。

它需要很大的计算资源。

为了考察层流火焰的某些特征（如火焰速度和厚度）以及这些特征与燃烧参数如燃料类型、化学配比、压力及未燃气体的温度的关系，对方程组进行了简化，以便能分析求解。

要得到简化的模型，需要引入一系列的假设。

我们从考察参考系建立在火焰上的层流火焰结构的某些方面入手。

如前所述，这些计算是针对等压过程进行的。

但是对一维缓燃的Rankine-Hugoniot 曲线，如图2 所示，已燃气的压力小于未燃气的压力。

现在我们需要考察压力减少的数值是否小到可以忽略的程度。

层流火焰与湍流火焰的结构一、层流火焰分析层流火焰速度和火焰结构一维层流火焰在预混燃料-氧化剂混合物中传播是最简单的燃烧现象之一，在此火焰中，化学动力学以及能量和组分扩散输运起重要作用。

通过守恒方程和状态方程可以导出Rankine-Hugoniot 曲线。

该曲线把在一维层流预混火焰中未燃气和已燃气状态联系起来。

已燃气体位于Rankine-Hugoniot 曲线下分支（缓燃），并相应于未燃气体状态Rayleigh 线与具有适当反应热的Rankine-Hugoniot 曲线交点L，如图1-2中所示。

图1 层流预混火焰坐标系图 2 一维燃烧波的Rankine-Hugoniot 曲线和Rayleigh 线Rayleigh 线的斜率与相对于未燃气体的波的传播速度，即层流火焰速度有关。

/ ( / )2 ( )2 u u dP dv = −m& A = −ρu(= ) = u u u S 层流火焰速度= (1/ ) (dP / dv) u −ρ由于缓燃Rayleigh 线斜率比爆震Rayleigh 线斜率小得多，所以缓燃速度比爆震速度小得多。

虽然守恒方程和状态方程提供了缓燃的未燃气体和已燃状态之间的关系，但不能唯一确定层流火焰速度Su 。

为了确定Su ，必须将守恒方程通过缓燃波积分。

由于 96方程是非线性耦合微分方程，其准确解只有通过数值积分才能获得。

它需要很大的计算资源。

为了考察层流火焰的某些特征（如火焰速度和厚度）以及这些特征与燃烧参数如燃料类型、化学配比、压力及未燃气体的温度的关系，对方程组进行了简化，以便能分析求解。

要得到简化的模型，需要引入一系列的假设。

我们从考察参考系建立在火焰上的层流火焰结构的某些方面入手。

如前所述，这些计算是针对等压过程进行的。

但是对一维缓燃的Rankine-Hugoniot 曲线，如图2 所示，已燃气的压力小于未燃气的压力。

现在我们需要考察压力减少的数值是否小到可以忽略的程度。