节约里程法案例详解

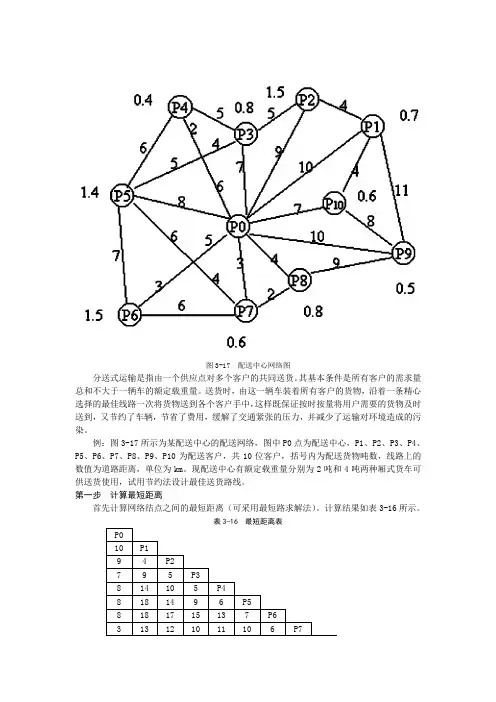
图3-17 配送中心网络图分送式运输是指由一个供应点对多个客户的共同送货。

其基本条件是所有客户的需求量总和不大于一辆车的额定载重量。

送货时，由这一辆车装着所有客户的货物，沿着一条精心选择的最佳线路一次将货物送到各个客户手中，这样既保证按时按量将用户需要的货物及时送到，又节约了车辆，节省了费用，缓解了交通紧张的压力，并减少了运输对环境造成的污染。

例：图3-17所示为某配送中心的配送网络，图中P0点为配送中心，P1、P2、P3、P4、P5、P6、P7、P8、P9、P10为配送客户，共10位客户，括号内为配送货物吨数，线路上的数值为道路距离，单位为km。

现配送中心有额定载重量分别为2吨和4吨两种厢式货车可供送货使用，试用节约法设计最佳送货路线。

第一步计算最短距离首先计算网络结点之间的最短距离（可采用最短路求解法）。

计算结果如表3-16所示。

表3-16 最短距离表第二步计算节约里程根据最短距离结果，计算出各客户之间的节约行程，结果见表3-17所示。

表3-17 节约里程表第三步将节约里程进行分类对节约行程按从大到小的顺序排列，如表3-18所示。

表3-18 节约里程排序第四步确定配送线路按节约里程大小顺序，组成线路图。

1、初始方案：如图3-18所示，从配送中心P0分别向各个客户进行配送，对每一客户分别单独派车送货，共有10条配送线路，总行程为148公里，需2吨货车10辆。

2、修正方案1：图3-18 图3-19按照节约行程的由大到小的顺序，连接P1和P2，P1和P10，P2和P3，P3和P4，形成巡回路线P0-P10-P1-P2-P3-P4-P0的配送线路，如图所示，装载货物4吨，这时配送路线总运行距离为109公里，配送线路6条，需4吨货车1辆，需2吨货车5辆，如图3-19所示。

3、修正方案2：按节约里程由大到小的顺序，连接P5和P6，P6和P7，形成巡回路线P0-P5-P6-P7-P0的配送线路，如图所示，装载货物3.5吨，这时配送路线总运行距离为85公里，配送线路4条，需4吨货车2辆， 图3-20 需2吨货车2辆，如图3-20所示。

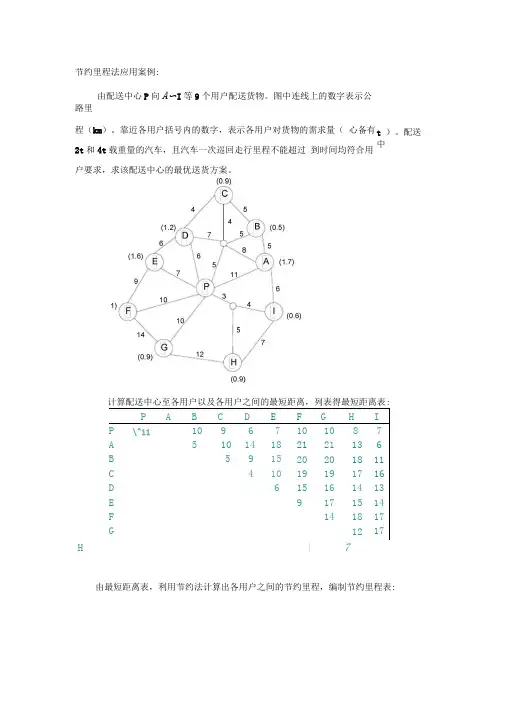
节约里程法应用案例:
由配送中心P向A〜I等9个用户配送货物。

图中连线上的数字表示公
路里
程（km）。

靠近各用户括号内的数字，表示各用户对货物的需求量（心备有
2t和4t载重量的汽车，且汽车一次巡回走行里程不能超过到时间均符合用
户要求，求该配送中心的最优送货方案。

计算配送中心至各用户以及各用户之间的最短距离，列表得最短距离表:
P A B C D E F G H I P \^1110 9 6 710 10 8 7
A 5 10 14 18 2121 136
B 5 9 1520 20 1811
C 4 1019 19 17 16
D 6 15 16 14 13
E 9 17 15 14
F 14 18 17
G 12 17
H \ 7
由最短距离表，利用节约法计算出各用户之间的节约里程，编制节约里程表:
t ）。

配送
中
A B c D E F G H I
A 16 10 3 0 0 0 6 12
B14 7 2 0 0 0 6
C 11 6 0 0 0 0
D 7 10 0 0
E -8 0 00
F 6 00
G 6 0
H8
1
根据节约里程表中节约里程多少的顺序，由大到小排列，编制节约里程顺序表，以便尽量使节约里程最多的点组合装车配送。

束条件，渐进绘出配送路径:
6
A
B
6
D
o
- 1
E
6
6
c
9
A
径 B
径 c
径
1 1
9) a。

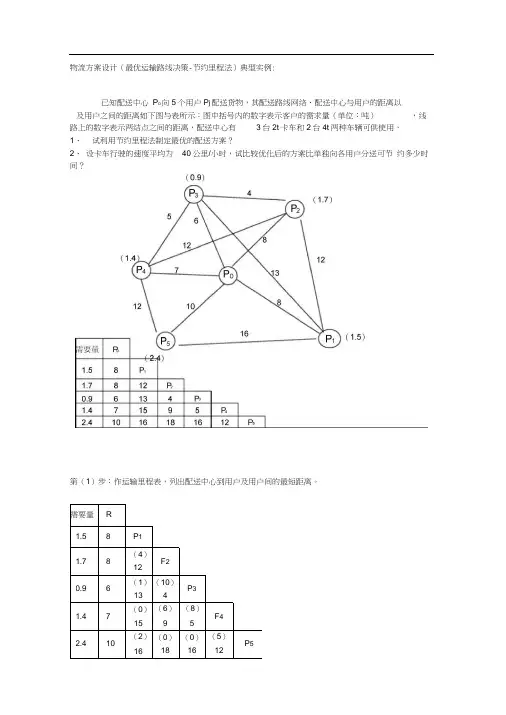
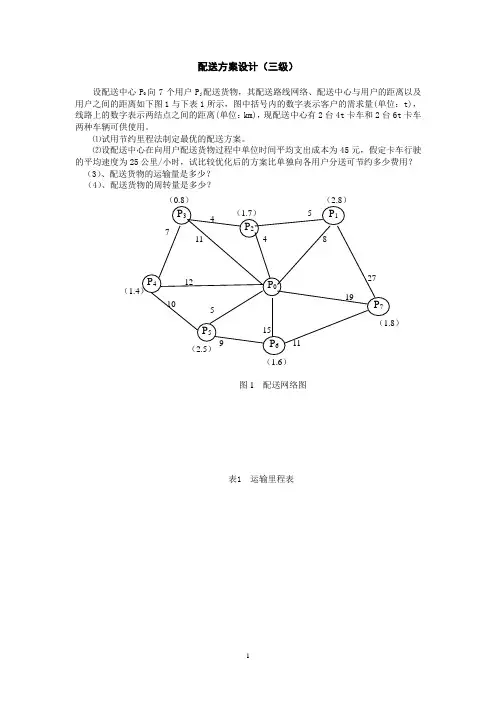
物流方案设计（最优运输路线决策-节约里程法）典型实例:已知配送中心P O向5个用户P j配送货物，其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示：图中括号内的数字表示客户的需求量（单位：吨），线路上的数字表示两结点之间的距离，配送中心有3台2t卡车和2台4t两种车辆可供使用，1、试利用节约里程法制定最优的配送方案？2、设卡车行驶的速度平均为40公里/小时，试比较优化后的方案比单独向各用户分送可节约多少时间？第（1）步：作运输里程表，列出配送中心到用户及用户间的最短距离。

得初始方案配送距离=39X 2=78KM第（5）步：根据载重量约束与节约里程大小，将各客户结点连接起来，形成二个配送路线。

即A B 两配送方案。

序号 路线 节约里程 序号 路线 节约里程1 P 2P 3 10 6 P i F 52 2 P 3P 4 8 7 P i P3 1 3 P 2P4 6 8 F 2F5 0 4 P 4P 5 5 9 F 3F 5 0 5P l P 2410P i F 4第（2）步：由运输里程表、按节约里程公式，求得相应的节约里程数，如上表（ 第（3）步：将节约里程 sij 进行分类，按从大到小顺序排列第（4）步：确定单独送货的配送线路）内。

(1.5)①配送线路A：P0-P2-P3-P4- P 0 运量q A= q 2+q3+q4 = 1.7+0.9+1.4 = 4t 用一辆4t 车运送节约距离S A =10 +8 = 18km②配送线路B: P 0-P5 -P 1-P0 运量q B =q 5+q1=2.4+1.5=3.9t<4t 车用一辆4t 车运送节约距离S B=2km第（6）步：与初始单独送货方案相比，计算总节约里程与节约时间总节约里程：△ S= S A+S B= 20 km与初始单独送货方案相比，可节约时间：△T = △ S/V=20/40=0.5小时。

配送路径优化节约里程法事例一、配送的困扰说起配送这事儿，大家都有点经验吧？那种看似简单、实则复杂的送货过程，光是坐车的时间都能让人崩溃。

有时候就算是个小小的东西，送到手里的时间也不一定那么准时。

你看，那些送货员的车，东绕西绕的，绕了半天，回头一看，距离目的地明明就不远，怎么感觉走了好几条弯路，浪费了不少油，吃了不少时间。

说得通俗点，那就是配送路径没优化好！你说，谁家不想节省点里程呢？这不仅能省钱，还能节省油费，最重要的是，减少了送货员心里的压力。

所以啊，这个配送路径优化的事儿，真的得好好琢磨一番。

二、路径优化的作用那这优化到底是个啥意思呢？如果送货员每次都能按照最短的路程走，不用左拐右绕，不用在每个交叉路口犹豫半天，效率自然就高了。

这种“少走弯路”的办法，不仅能节省时间，车辆油耗也会降低，大家的心情也能轻松点。

你想想，不再碰到那种“导航指路，车却走偏”的尴尬局面，不再在车里等个十几分钟，真的是大大的爽。

再加上现在的技术那么先进，有了路径优化，送货员的负担轻了，企业的运营成本也降低了，一举两得，岂不是美滋滋？但是，如何优化呢？这可不是那么简单的事儿，得好好分析。

得从每一个配送的起点和终点开始算，合理规划每一条路线。

有的配送中心本来就不远，但因为道路复杂、交通状况不好，结果走了许多不必要的冤枉路。

你要知道，那种高峰期的交通，光是堵个红绿灯，差不多就得半小时过去。

再加上，某些路段的繁忙程度，早高峰、晚高峰的时候可不是闹着玩的。

那种时间上的浪费，实在是让人心烦。

你能想象吗？你本来预计一个小时就能到的地方，结果送了两小时才到，最后客户也没了耐心，甚至还得打个电话投诉。

那场面可真是尴尬死了。

三、具体实施路径优化说到这里，很多人可能就会问了，那要怎么实施路径优化呢？其实现在有很多高效的系统，可以根据实际情况帮你算出最短路径。

比如，根据每条道路的交通状况、道路的宽窄程度、甚至是天气情况来优化路线。

你要知道，不是所有的道路都能通行，尤其在一些小巷子里，车子一进去了，根本就转不过来。

节约里程法应用案例在当今竞争激烈的商业环境中，物流成本的有效控制对于企业的生存和发展至关重要。

节约里程法作为一种优化配送路线的有效方法，能够显著降低运输成本，提高物流效率。

接下来，让我们通过一个具体的案例来深入了解节约里程法的实际应用。

假设我们有一家位于城市中心的配送中心，需要向位于城市不同区域的五个客户（A、B、C、D、E）配送货物。

每个客户的需求量以及他们之间的距离如下表所示：｜客户|需求量（吨）｜与配送中心距离（公里）｜｜｜｜｜｜A|5|10|｜B|8|12|｜C|3|8|｜D|6|15|｜E|4|11|｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 18 ｜ 22 ｜ 25 ｜ 16 ｜｜B| 18 ｜｜ 10 ｜ 18 ｜ 12 ｜｜C| 22 ｜ 10 ｜｜ 14 ｜ 9 ｜｜D| 25 ｜ 18 ｜ 14 ｜｜ 20 ｜｜E| 16 ｜ 12 ｜ 9 ｜ 20 ｜｜首先，我们按照传统的方法，即每个客户单独配送，计算出总运输里程。

配送中心到客户 A 的往返里程为 2×10 ＝ 20 公里。

配送中心到客户 B 的往返里程为 2×12 ＝ 24 公里。

配送中心到客户 C 的往返里程为 2×8 ＝ 16 公里。

配送中心到客户 D 的往返里程为 2×15 ＝ 30 公里。

配送中心到客户 E 的往返里程为 2×11 ＝ 22 公里。

总运输里程为 20 ＋ 24 ＋ 16 ＋ 30 ＋ 22 ＝ 112 公里。

接下来，我们应用节约里程法来优化配送路线。

第一步，计算两两客户之间的节约里程数。

例如，客户 A 和客户 B 之间的节约里程数为：（配送中心到 A 的距离＋配送中心到 B 的距离 A 到 B 的距离）× 2 ＝（10 ＋ 12 18）× 2 ＝ 8 公里。

按照同样的方法，计算出所有两两客户之间的节约里程数，如下表所示：｜客户|A|B|C|D|E|｜｜｜｜｜｜｜｜A| ｜ 8 ｜ 6 ｜ 5 ｜ 2 ｜｜B| 8 ｜｜ 4 ｜ 3 ｜ 4 ｜｜C| 6 ｜ 4 ｜｜ 2 ｜ 3 ｜｜D| 5 ｜ 3 ｜ 2 ｜｜ 5 ｜｜E| 2 ｜ 4 ｜ 3 ｜ 5 ｜｜第二步，根据节约里程数的大小对路线进行合并和优化。

节约里程法例题
问题描述
某公司为了降低员工的交通成本，制定了节约里程法，规定员工在每周的通勤过程中，只能行驶一定的里程数。

具体规定如下：
•每位员工每周最多行驶300公里的里程数；
•员工每行驶一公里，公司会额外支付0.5元。

现在需要使用节约里程法计算员工每周的交通费用。

算法设计
节约里程法的核心思想是根据员工的行驶距离来计算交通费用。

算法的基本步骤如下：
1.设置变量total_mileage为员工总行驶里程数，初始值为0；
2.设置变量total_cost为员工总交通费用，初始值为0；
3.循环执行以下步骤：
–输入本次行驶的里程数mileage；
–如果mileage + total_mileage大于300，则将total_cost 增加300 - total_mileage * 0.5，并将total_mileage更新为300；
–否则，将total_cost增加mileage * 0.5，并将
total_mileage增加mileage；
–如果total_mileage等于300，则退出循环。

4.输出员工总交通费用total_cost。

算法实现
以下是使用Python语言实现节约里程法的代码示例：
```python def calculate_transport_cost(): total_mileage = 0 total_cost = 0
while total_mileage < 300:
mileage = float(input(\。

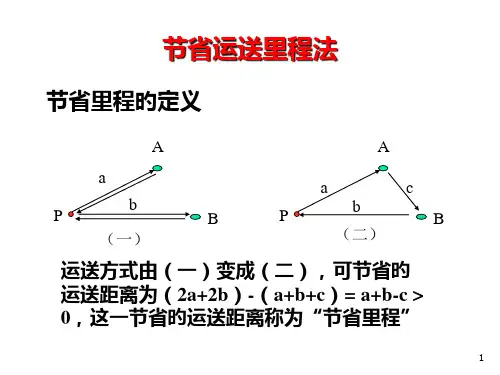
节约里程法1.原理设P 为配送中心，A 和B 为收货点，相互之间的道路距离为a , b , c 。

若分别使用两辆货车分别向A 、B 两地往返送货，其行驶里程为:2a+2b 。

但若使一辆货车（货车可以满载两地送货）由P → A →B →P ，单线巡回送货，其行驶总里程为a+c+b 。

两者相比，后一种方案比前一种送货方案可节省的运输距离是： （2a+2b ）-（a+c+b ）= a + b - c > 0这一节约距离称为节约里程，所以我们称这种方法为“节约里程法”。

2 .实例由于案例所给内容有限，所以我们自行上网查找了一些资料。

下图是我们找到的位于郑明现代物流有限公司上海总部周边的一些大型商超，下面我们就假设这些超市为郑明现代物流有限公司的配送点，利用节约里程法来设计末端配送网络的合理运输。

上海郑明现代物流有限公司周边的商超配送点PABacb图X-X备注：1 . 红色五角星所在位置即为郑明现代物流有限公司的所在地(P)2 . 紫色圆圈即为超市配送点的位置及其名称（从左至右依次为：城市超市(A)、沃尔玛超市(B)、世纪华联超市(C)、联华超市(F)、家乐福超市(D)、大润发超市(E)）为直观清晰的了解郑明现代物流有限公司与给超市配送点之间的关系，我们将上图简化为下图（图X-X）的简易图形。

线段旁的数字为两者之间的距离，单位：km.图X-X节约里程法的求解过程如下：1.计算配送中心P 到各个配送点及各配送点之间的最短路距离，如下表最短距离表P ABCDEFP A 4.7B 2.8 6.8C 0.6 4.2 2.9D 8 12.7 6.1 8.6E 7.4 12.1 9.2 8 3.1F1.83.24.62.49.89.14.26.12.96.80.62.883.17.49.11.83.2BDFA C EP2.计算各个配送点之间的节约里程，如下表节约里程表A B C D E FAB 0.7C 1.1 0.5D 0 4.7 0E 0 1 0 12.3F 3.3 0 0 0 0.13.进行排序：节约里程排序表序号连接节约序号连接节约1 DE 12.3 8 AD 02 BD 4.7 9 AE 03 AF 3.3 10 BF 04 AC 1.1 11 CD 05 AB 0.7 12 CE 06 BC 0.5 13 CF 07 EF 0.1 14 DF 04.得出线路安排线路一：P →E →D →B →P 节约里程为：12.3+4.7= 17 km 线路二：P →F →A →C →P 节约里程为：3.3+1.1= 4.4 km如果没有使用节约里程法来进行商超的配送，那么结果是怎样的呢？假定初始配送方案是由中心点P 按最短路径向其余各个点分别进行送货，则总配送里程为：2x(0.6+4.2+1.8+7.4+8+2.8)=49.6 km 。

节约里程法案例详解假如由一家配送中心P向两个用户A、B送货，配送中心到两客户的最短距离分别是L1和L2，A和B间的最短距离为L3，AB的货物需求量分别是Q1和Q2，且Q1+Q2小于车辆装载量Q【如果Q1+Q2大于车辆装载量Q，那一辆车就无法装完两位客户的货物】。

如下图所示：如果配送中心用两辆汽车分别对A、B两个用户各自往返送货时，汽车行驶的总里程L是L=2（L1+ L2）如果用一辆汽车向A、B两个用户巡回送货，则汽车行驶总里程L′为L′= L1+ L2+L3根据三角形的一边之长必定小于另外两边之和的原理，后一种配送方案比前一种方案节约里程△L为△L=2（L1+ L2）-（L1+ L2+L3）= L1+ L2-L3【这就是节约里程法产生的初衷，以最短距离最优配载完成送货作业】案例：位于市内的百家姓配送中心（P0）向它旗下的10家连锁商店p i(i=1,2,…,10)配送商品，其配送网络如下图所示。

图中括号内的数字表示每一家连锁店的需求量（t），线路上的数字表示两节点之间的距离（km）。

配送中心现有2t和4t车辆可供使用（无数量限制），并且每辆车配送距离不得超过30km。

请为百家姓配送中心制定最优的配送方案。

分析：初始方案：如果从P点向各点分别派车送货。

1、从百家姓配送中心出发，需要设计10条配送线路，分别向10家连锁店配送商品；2、需要10辆2t的配送车辆（每家连锁店的需要量都低于2t），总配送距离为148km。

第二种：节约里程法解题思路：相互间的节约里程计算根据△L== L1+ L2-L3 原理，例如以“百家姓配送中心交通图”中的P0（配送中心）到客户d、客户c的节约里程为例：dc△L==P0d(L1)+P0c (L2)-dc(L3 )==8 + 7 - 5=10如此计算出客户d和客户c间的节约里程数为10，以此方法计算出各个节点的节约里程数。

方案修正过程（优化到最终线路）1、方案修正过程实际上是线路规划过程，根据节约里程法原理从节约里程数最大的节点开始选择（这是先要排序的原因）；2、所有规划线路的起点和终点都是配送中心，这里是P0；3、最大节约里程是a和b间的节约里程数15，那么路线的走向可以是P0-A或P0-B。

由配送中心A 向两个用户M 、N 送货，A 至M 、N 的最短距离分别为l1和l2，M 、N 之间的距离为l3，用户M 、N 对货物的需求量分别为q1和q2。

如图：若用两辆汽车分别对A 、B 两个用户所需货物，各自往返送货时，汽车直行总里程为：l=2（l1+l2）如果改为有一辆汽车向M 、N 两个用户巡回送货（设q1+q2<汽车标重载重量），则汽车走行里程为： l=l1+l2+l3后一种送货方案比前一种送货方案节约的汽车走行里程为： △l=[2（l1+l2）]-（l1+l2+l3）=l1+l2-l34 案例分析如图所示：由配送中心P 向A-H8个用户配送货物。

图中连线上的数字表示两点间的里程（km ），图中靠近个用户括号内的数字，表示各用户对货物的需求量（t ）。

配送中心备有2t 和3t 载重量的汽车，且汽车一次巡回里程不超过35km 。

色送到时间均符合客户要求。

求改配送中心的最优送货方案。

﹙q1﹚（q2）节约里程表A B C D E F G HA 9 2 0 0 0 0 7B 8 5 0 0 0 6C 11 3 0 0 0D 10 5 0 0E 9 2 0F 13 3G 6H根据节约里程表中节约里程的顺序，由大到小排列，编制节约里程顺序表。

节约里程顺序表根据节约里程顺序表和配车（车辆的载重），车辆行驶里程等约束条件，渐进绘出如图所示配送路径.路径A：2t车，走行24km，载重量1.8t。

路径B：3t车，走行33km，载重量3.0t。

路径C：3t车，走行23km，载重量2.8t。

总共行走80km，节约里程60km。

从图中可看：一次确定的A、B、C三条路径均符合配送中心的约束条件。

需要2t汽车1辆，3t汽车2辆，总走行里程为80km，若简单的每个用户派一辆汽车配送，需要2t汽车8辆，走行总里程为140km。

通过比较可以看出，利用节约里程法制定配送方案确定送货路径，具有明显效果。

节约里程算法在物流配送领域，如何优化配送路线以降低成本、提高效率是一个关键问题。

节约里程算法就是为解决这一问题而诞生的一种有效方法。

要理解节约里程算法，首先得清楚什么是里程节约。

简单来说，就是通过合理规划配送路线，减少车辆行驶的总里程数。

比如说，有三个配送点 A、B、C。

如果车辆单独从配送中心去 A，再回配送中心，里程是 50 公里；单独去 B 再回，里程是 60 公里；单独去 C 再回，里程是 70 公里。

但如果先去 A，再去 B，最后回配送中心，总里程可能就不是 50 ＋ 60 ＝ 110 公里，而是 90 公里。

这节省的20 公里就是节约的里程。

节约里程算法的核心思想就是通过计算不同配送点组合之间的里程节约值，来确定最优的配送路线。

那么，它是怎么计算里程节约值的呢？我们以两个配送点 i 和 j 为例。

假设单独从配送中心到 i 的里程是 C1，单独到 j 的里程是 C2，而从配送中心经过 i 再到 j 的里程是 C3。

那么，这两点之间的里程节约值 Sij 就可以通过以下公式计算：Sij ＝ C1 ＋ C2 C3 。

接下来，我们通过一个具体的例子来看看节约里程算法是如何工作的。

假设有 7 个配送点，分别是 P1、P2、P3、P4、P5、P6、P7，它们与配送中心的距离以及相互之间的距离如下表所示：｜配送点|与配送中心距离|相互之间距离|｜｜｜｜｜P1|20 公里| ｜｜P2|30 公里| ｜｜P3|25 公里| ｜｜P4|18 公里| ｜｜P5|28 公里| ｜｜P6|22 公里| ｜｜P7|15 公里| ｜｜｜P1|P2|P3|P4|P5|P6|P7|｜｜｜｜｜｜｜｜｜｜P1| ｜12|8 ｜10|16|9 ｜7 ｜｜P2|12| ｜6 ｜15|8 ｜10|12|｜P3|8 ｜6 ｜｜7 ｜11|5 ｜9 ｜｜P4|10|15|7 ｜｜18|8 ｜10|｜P5|16|8 ｜11|18| ｜12|14|｜P6|9 ｜10|5 ｜8 ｜12| ｜6 ｜｜P7|7 ｜12|9 ｜10|14|6 ｜｜第一步，计算所有配送点之间的里程节约值。

节约里程法及举例1当由一个配送中心向多个客户进行共同送货，在一条线路上的所有客户的需求量总和不大于一辆车的额定载重量时，由这一辆车配装着所有客户需求的货物，按照一条预先设计好的最正确路线依次将货物送到每一客户手中，这样既可保证按需将货物及时送交，同时又能节约行驶里程，缩短整个送货时间，节约费用。

节约里程法正是用来解决这类问题的较成熟的方法。

用节约里程法确定配送路线的主要思路是，根据配送中心的运输能力及其到各客户之间的距离和各客户之间的相对距离，来制定使总的配送车辆吨公里数到达或接近最小的配送方案。

节约里程法的根本思路如下图，P 为配送中心所在地，A 和B 为客户所在地，相互之间道路距离分别为a 、b 、c 。

最简单的配送方法是利用两辆车分别为A 、B 客户配送，此时，如图〔b 〕所示，车辆运行距离为2a 2b 。

然而，如果按图〔c 〕所示改用一辆车巡回配送，运行距离为abc 。

如果道路没有什么特殊情况，可以节省的车辆运行距离为2a 2b –abc =ab –c >0，这个节约量“ab –c 〞被称为“节约里程〞。

AAABPPPB（a ）物流网络（c ）用一辆车配送ac ba cb ab c图 配送中心配送路线的选择1郑克俊仓储与配送管理〔第四版〕科学出版社 修订。

步骤：实际上如果给数十家、数百家客户配送，〔1〕应首先计算包括配送中心在内的相互之间的最短距离，〔2〕然后计算各客户之间的可节约的运行距离，〔3〕按照节约运行距离的大小顺序连结各配送地并设计出配送路线。

下面举例说明节约里程法的求解过程。

例节约里程法举例图为某配送网络，P为配送中心所在地，A～J为客户所在地，共10个客户，括号内的数字为配送量〔单位：吨〕，路线上的数字为道路距离〔单位：千米〕。

现有可以利用的车辆是最大装载量为2吨和4吨的两种厢式货车，并限制车辆一次运行距离在30千米以内。

为了尽量缩短车辆运行距离，试用节约里程法设计出最正确配送路线。

例：有一配送（P）具有如图所示的配送网络，其中A-J表示收货站，（）内数字表示发送量（吨），路线上的数字表示道路距离（公里）。

问为使行走距离尽量小，应该如何去求配送线路？假设能够利用的车是2吨车（即最大载重量是2吨）和4吨车两种，并限制车辆一次运行的初步距离是30公里。

解题步骤：1.第一步：作出最短距离矩阵，首先从配送网络图中计算出配送中心与收货点之间以及收货点相互之间的最短距离矩阵，见下表所示：表一：最短距离矩阵（单位：公里）例如：计算A-B的节约里程项目如下：P-A的距离是：a=10P-B的距离是：b=9A-B的距离是：c=4节约里程项目为：a+b-c=10+9-4=15公里3.第三步：节约项目分类，再把节约项目由大到小顺序排列。

（1）.初次解。

线路数：10总行走距离：(10+9+7+8+8+8+3+4+10+7)*2=148公里车辆台数：2吨车10台（2）.二次解。

按节约里程由大到小的顺序，连接A-B，A-J，B-C连接线。

线路数：7总行走距离：148-15-13-11=109公里车辆台数：2吨车6台，4吨车1台（3）.三次解。

其次节约里程最大的是C-D和D-E。

C-D，D-E两者都有可能与二次解的线路A连接，但由于A的车辆载重量与行走距离有限，不能再增加收货点。

为此，略去C-D而连接D-E。

总行走距离：109-10=99公里车辆台数：2吨车5台，4吨车1台（4）.四次解。

接下来节约里程大的是A-I和E-F。

由于A已组合在完成的线路A中，所以略去，不能再增加收货点。

为此，略去A-I 而将E-F连接在线路B上。

线路数：5总行走距离：99-9=90公里车辆台数：2吨车3台，4吨车2台（5）.五次解。

再继续按节约里程由大到小排出I-J，A-C，B-J，B-D，C-E。

由于同一组总有一头或两头包含在已完成的线路A中，不能再作出新的线路。

只考虑把下一组F-G组合在完成的线路B中。

总行走距离：85公里车辆台数：2吨车2台，4吨车2台线路A：4吨车，总行走距离27公里，装载量3.6吨。