物流工程——节约里程法
- 格式:ppt
- 大小:1.33 MB
- 文档页数:29


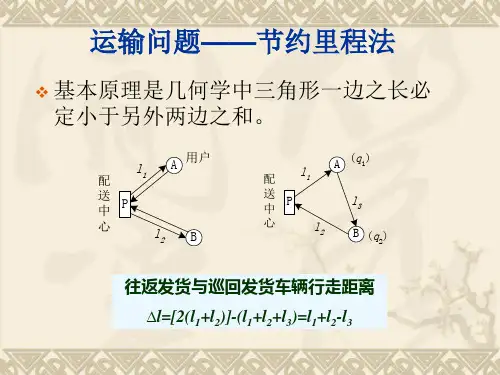
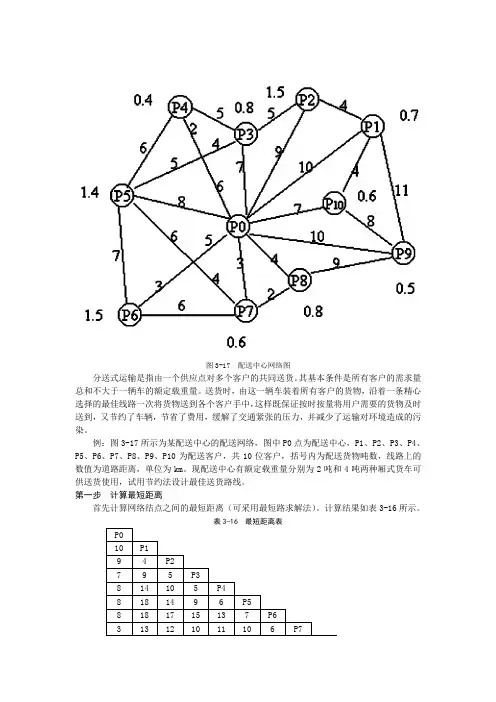
图3-17 配送中心网络图分送式运输是指由一个供应点对多个客户的共同送货。
其基本条件是所有客户的需求量总和不大于一辆车的额定载重量。
送货时,由这一辆车装着所有客户的货物,沿着一条精心选择的最佳线路一次将货物送到各个客户手中,这样既保证按时按量将用户需要的货物及时送到,又节约了车辆,节省了费用,缓解了交通紧张的压力,并减少了运输对环境造成的污染。
例:图3-17所示为某配送中心的配送网络,图中P0点为配送中心,P1、P2、P3、P4、P5、P6、P7、P8、P9、P10为配送客户,共10位客户,括号内为配送货物吨数,线路上的数值为道路距离,单位为km。
现配送中心有额定载重量分别为2吨和4吨两种厢式货车可供送货使用,试用节约法设计最佳送货路线。
第一步计算最短距离首先计算网络结点之间的最短距离(可采用最短路求解法)。
计算结果如表3-16所示。
表3-16 最短距离表第二步计算节约里程根据最短距离结果,计算出各客户之间的节约行程,结果见表3-17所示。
表3-17 节约里程表第三步将节约里程进行分类对节约行程按从大到小的顺序排列,如表3-18所示。
表3-18 节约里程排序第四步确定配送线路按节约里程大小顺序,组成线路图。
1、初始方案:如图3-18所示,从配送中心P0分别向各个客户进行配送,对每一客户分别单独派车送货,共有10条配送线路,总行程为148公里,需2吨货车10辆。
2、修正方案1:图3-18 图3-19按照节约行程的由大到小的顺序,连接P1和P2,P1和P10,P2和P3,P3和P4,形成巡回路线P0-P10-P1-P2-P3-P4-P0的配送线路,如图所示,装载货物4吨,这时配送路线总运行距离为109公里,配送线路6条,需4吨货车1辆,需2吨货车5辆,如图3-19所示。
3、修正方案2:按节约里程由大到小的顺序,连接P5和P6,P6和P7,形成巡回路线P0-P5-P6-P7-P0的配送线路,如图所示,装载货物3.5吨,这时配送路线总运行距离为85公里,配送线路4条,需4吨货车2辆, 图3-20 需2吨货车2辆,如图3-20所示。


"节约里程法"英文翻译:节约里程法(Saving Algorithm)内容摘要:节约里程法又称节约算法,是指用来解决运输车辆数目不确定的VRP问题的最有名的启发式算法。
什么是节约里程法节约里程法又称节约算法,是指用来解决运输车辆数目不确定的VRP问题的最有名的启发式算法。
节约里程法的基本原理节约里程法的基本思路如下图,已知O点为配送中心,它分别向用户A和B送货。
设O点到用户A和用户B的距离分别为a和b。
用户A和用户B之间的距离为c,现有两种送货方案,如图下(a)和(b)所示。
在上图(a)中配送距离为2(a+b);图上(b)中,配送距离为a+b+c。
对比这两个方案,哪个更合理呢?这就要看哪个配送距离最小,配送距离越小,则说明方案越合理。
由上图(a)中的配送距离,减去图1(b)中的配送距离可得出:2(a+b)-(a+b+c)=(2a+2b)-a-b-c=a+b-c(1)如果把上图(b)看成一个三角形,那么a、b、c则是这个三角形三条边的长度。
由三角形的几何性质可知,三角形中任意两条边的边长之和,大于第三边的边长。
因此,可以认定(1)式中结果是大于零的。
即:a+b-c>0(2)由(2)式可知,(b)方案优于(a)方案,节约了(a+b-c)的里程,这种分析方案的优劣式的思想,就是节约里程法的基本思想。
、拓展资料:一、节约里程法核心思想节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路,每次使合并后的总运输距离减小的幅度最大,直到达到一辆车的装载限制时,再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
二、节约里程法示例例:有一配送P具有如图所示的配送网络,其中A-J表示收货站,()内数字表示发送量(吨),路线上的数字表示道路距离(公里)。
问为使行走距离尽量小,应该如何去求配送线路?假设能够利用的车是2吨车(即最大载重量是2吨)和4吨车两种,并限制车辆一次运行的初步距离是30公里。




节约里程法(Saving Algorithm)•车辆调度程序法(Vehicle Scheduling Program:VSP)•又称节约算法,是指用来解决运输车辆数目不确定的问题的最有名的启发式算法。
核心思想:•节约里程法核心思想是依次将运输问题中的两个回路合并为一个回路,每次使合并后的总运输距离减小的幅度最大,直到达到一辆车的装载限制时,再进行下一辆车的优化。
优化过程分为并行方式和串行方式两种。
节约里程法•利用节约法制定出的配送方案除了使配送总吨公里数最小外,还应满足以下条件:–满足所有用户的需求–不使任何一辆车超载–每辆车每天的总运行时间或行驶里程不超过规定的上限;–用户到货时间要求。
不得超过规定时间。
节约里程法PA(客户)B(客户)ab(配送中心)PA(客户)B(客户)(配送中心)ba c运行距离为:2a+2b运行距离为:a+b+c 节约行程:a + b-c节约里程法例题:已知配送中心P 0向5个用户P j 配送货物,其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图所示,配送中心有3台2t卡车和2台4t两种车辆可供使用。
利用节约里程法制定最优的配送方案。
(1.4)P 0P 2P 3P 4P 5P 1( 2.4 )( 0.9 )(1.7)(1.5 )101275124136812168节约里程法•第1 步:作运输里程表,列出配送中心到用户及用户间的最短距离。
需求量P0P11.58P1P21.7812P2P30.96134P3P41.471595P4P52.41016181612P5节约里程法第2步:按节约里程公式求得相应的节约里程数需求量P01.58P11.7812P2 40.96134P3 1101.471595P4 0682.41016181612P5 2005节约里程法第3 步:将节约里程按从大到小顺序排列序号路线节约里程1P2P3102P3P483P2P464P4P555P1P246P1P527P1P318P2P509P3P5010P1P40节约里程法第4步:根据载重量约束与节约里程大小,顺序连接各客户结点,形成二个配送路线.P2P3-P3P4-P2P4-P4P5-P1P2-P1P5-P1P3 -P2P5 -P3P5-P1P4(1.4)P 0P 2P 3P 4P 5P 1(2.4)(0.9)(1.7)(1.5)10768845节约里程法(1.4)P 0P 2P 3P 4P 5P 1(2.4)(0.9)(1.7)(1.5)1078845配送线路1节约里程法(1.4)P 0P 2P 3P 4P 5P 1(2.4)(0.9)(1.7)(1.5)1078845配送线路1配送线路1:运量= 1.7+0.9+1.4= 4t运行距离=8+4+5+7=24km用一辆4t 车运送节约距离=18km配送线路2: 运量=2.4+1.5=3.9t<4t 运行距离=8+10+16=34km 用一辆4t 车运送节约距离=2km节约里程法(1.4)P 0P 2P 3P 4P 5P 1(2.4)(0.9)(1.7)(1.5)107688初始方案:配送线路5条,需要车5辆配送距离=39×2=78KM节约里程法•初始方案:–配送线路5条,需要车5辆–配送距离:39×2=78KM•优化后的方案:–2条配送线路,2辆4t车–配送距离:24+34=58km节约里程法案例:•宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优化方法。

节约里程法及举例1当由一个配送中心向多个客户进行共同送货,在一条线路上的所有客户的需求量总和不大于一辆车的额定载重量时,由这一辆车配装着所有客户需求的货物,按照一条预先设计好的最正确路线依次将货物送到每一客户手中,这样既可保证按需将货物及时送交,同时又能节约行驶里程,缩短整个送货时间,节约费用。
节约里程法正是用来解决这类问题的较成熟的方法。
用节约里程法确定配送路线的主要思路是,根据配送中心的运输能力及其到各客户之间的距离和各客户之间的相对距离,来制定使总的配送车辆吨公里数到达或接近最小的配送方案。
节约里程法的根本思路如下图,P 为配送中心所在地,A 和B 为客户所在地,相互之间道路距离分别为a 、b 、c 。
最简单的配送方法是利用两辆车分别为A 、B 客户配送,此时,如图〔b 〕所示,车辆运行距离为2a 2b 。
然而,如果按图〔c 〕所示改用一辆车巡回配送,运行距离为abc 。
如果道路没有什么特殊情况,可以节省的车辆运行距离为2a 2b –abc =ab –c >0,这个节约量“ab –c 〞被称为“节约里程〞。
AAABPPPB(a )物流网络(c )用一辆车配送ac ba cb ab c图 配送中心配送路线的选择1郑克俊仓储与配送管理〔第四版〕科学出版社 修订。
步骤:实际上如果给数十家、数百家客户配送,〔1〕应首先计算包括配送中心在内的相互之间的最短距离,〔2〕然后计算各客户之间的可节约的运行距离,〔3〕按照节约运行距离的大小顺序连结各配送地并设计出配送路线。
下面举例说明节约里程法的求解过程。
例节约里程法举例图为某配送网络,P为配送中心所在地,A~J为客户所在地,共10个客户,括号内的数字为配送量〔单位:吨〕,路线上的数字为道路距离〔单位:千米〕。
现有可以利用的车辆是最大装载量为2吨和4吨的两种厢式货车,并限制车辆一次运行距离在30千米以内。
为了尽量缩短车辆运行距离,试用节约里程法设计出最正确配送路线。
节约里程法的优化目标【原创实用版】目录1.引言2.节约里程法的定义和意义3.节约里程法的优化目标4.节约里程法的实施策略5.节约里程法的效果评估6.结论正文【引言】随着社会经济的发展,资源浪费问题日益严重,特别是在交通运输领域,里程浪费现象普遍存在。
为了解决这一问题,节约里程法应运而生。
作为一种优化运输路线的方法,节约里程法旨在减少运输过程中的无效里程,提高运输效率,降低运输成本,从而实现资源节约和环境保护。
本文将从节约里程法的定义和意义、优化目标、实施策略和效果评估等方面进行阐述。
【节约里程法的定义和意义】节约里程法是一种优化运输路线的方法,主要通过减少运输过程中的无效里程,提高运输效率,降低运输成本,实现资源节约和环境保护。
在现代物流和交通运输领域,节约里程法具有重要的实用价值和意义。
【节约里程法的优化目标】节约里程法的优化目标是在保证运输质量和时效的前提下,通过优化运输路线,减少运输过程中的无效里程,提高运输效率,降低运输成本。
具体包括以下几个方面:1.最短路径:通过优化运输路线,使运输距离最短,从而减少无效里程。
2.最优路线:在保证运输质量和时效的前提下,选择最优的运输路线,降低运输成本。
3.资源整合:通过节约里程法,实现运输资源的整合,提高运输效率,降低空驶率。
【节约里程法的实施策略】要实现节约里程法的优化目标,需要采取一系列实施策略,包括:1.建立科学的运输网络:根据运输需求和资源分布,建立科学的运输网络,为节约里程法提供基础支持。
2.引入先进的运输规划技术:运用运输规划技术,如路径规划算法、遗传算法等,实现运输路线的优化。
3.建立健全的监测和管理体系:通过建立健全的监测和管理体系,对运输过程进行实时监控和调度,确保运输效率和质量。
【节约里程法的效果评估】节约里程法的效果评估主要从以下几个方面进行:1.运输距离的减少:通过比较实施节约里程法前后的运输距离,评估其效果。
2.运输成本的降低:通过比较实施节约里程法前后的运输成本,评估其效果。
配送路线优化里程节约法在现代物流配送中,如何优化配送路线以降低成本、提高效率是企业关注的核心问题之一。
里程节约法作为一种实用且有效的方法,为解决这一难题提供了有力的工具。
首先,让我们来理解一下什么是里程节约法。
简单来说,里程节约法是通过比较不同配送路线的里程差异,找出能够节约里程的组合,从而优化配送路线。
想象一下,有两个客户点 A 和 B,分别距离配送中心为 d1 和 d2,两点之间的距离为 d3。
原本单独配送时,总里程为 2×(d1 + d2)。
但如果将这两个点合并在同一次配送中,总里程就变为了 d1 + d2 + d3。
通过这种方式计算出节约的里程,然后对多个客户点进行组合和比较,就能找到最优的配送路线。
那么,里程节约法的优势在哪里呢?其一,它能够显著降低运输成本。
通过减少不必要的里程,节省了燃油、车辆磨损等费用。
其二,提高了配送效率。
优化后的路线可以减少配送时间,提高客户满意度。
其三,有助于合理规划资源。
企业可以根据节约的里程和时间,更精确地安排车辆和人员。
要成功应用里程节约法,需要做好一系列的准备工作。
第一步是收集准确而详细的基础数据,包括客户的位置、需求量、配送中心的位置等。
这些数据的准确性直接影响到后续路线规划的质量。
第二步是对数据进行整理和分析,明确各个客户点之间的相对位置和距离关系。
在实际应用里程节约法时,需要遵循一定的步骤。
首先,计算出每个客户点之间的距离。
然后,根据距离计算出每两个客户点合并配送所能节约的里程。
接下来,按照节约里程的大小进行排序。
从节约里程最大的组合开始,依次考虑是否能够合并配送,同时要注意满足车辆的载重限制、配送时间限制等约束条件。
比如说,有一家配送企业,要为 10 个客户点进行配送。
通过计算和排序,发现客户点 C 和 D 合并配送的节约里程最大。
但在决定合并时,还需要检查车辆的载重是否能够满足 C 和 D 客户的总需求量。
如果满足,就可以将这两个点合并在同一次配送中。