级数教学PPT

无穷级数是高等数学的一个重要组成部分, 它是表示函数、研究函数的性质以及进行数值 计算的一种工具.
一、级数的基本概念
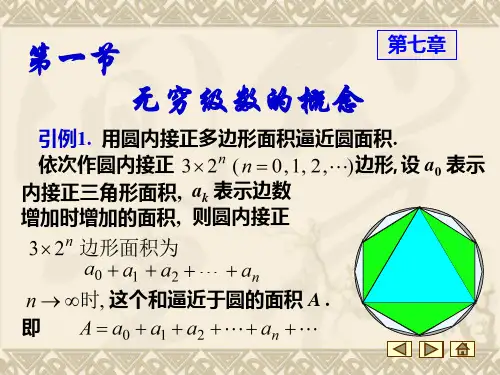
计算圆的面积
a1 正十二边形的面积 a1 a2 正 3 2 n 形的面积 a1 a2 an 即 A a1 a2 an
正六边形的面积
1
R
一般项
cos

2
n

lim cos

2
n
1 0 , 级数发散。
12
2、必要条件不充分：
若 lim un 0 , 级数却不一定收敛.
1 1 1 ) 0 ( n ) , 但级数发散。 如 ln( 1 ) : ln( n n n 1
再举一个重要例子：
n
1000 10000 1 1111 ， 1 9 9 1 10
7
1000 10000 1 1111 ， 1 9 9 1 10
也就是说,如果赛程比这个距离短,则乌龟胜；如果赛程恰好 等于这个距离,则双方平分秋色； 否则,阿基里斯就要在距离起点
1 1111 处追上并超过乌龟 . 9
8
n1 n1 n1
n



收敛；
(2) 若
un 收敛,而 vn
n 1 n 1

发散,则
(u
n1

vn ) 必发散.
证 假设
而已知
(u
n1

n
vn ) 收敛 , 由 vn (un vn ) un ,
由上述性质得
un 收敛 ,
n 1
n n

vn 收敛, 矛盾.
1000 100 100 100 米, 的时间为 ,在这段时间里,乌龟又爬了v 10v v v 100 10 阿基里斯为跑完这段路又花费时间 ,此时乌龟又在他前面 10v v
10 米处 , …… , 依次类推 , 阿基里斯需要追赶的全部路程为
1000 100 10
1 1 的几何级数 , 易求得它的和为 这是一个公比为 q 10
n1

(2) 如果级数
un 、 vn 都收敛,则 (un vn )
n 1 n 1 n 1


n1


也收敛,且有
（un vn ) un vn .
n1 n1 n1


由级数收敛的定义，以及极限的性质，不难证明。
15
注:
(1) 不能由

(un vn ) 收敛推出 un 、 vn
n 1

所以
(u v )
n1
发散 .
16
性质3 收敛级数任意加括号后仍收敛,且其和不变.
证略。
例如，若级数
un 收敛， 则级数
n 1
n1

(u
n 1

2 n 1
u2 n ) 、 (u3 n 2 u3n1 u3n ) 均收敛，
且和不变. 注 收敛级数去括弧后所成的级数不一定收敛. 例如 (1 1) (1 1) 推论 如果加括弧后所成的级数发散,则原级数也发散.
n 1
3

例1 讨论等比级数(几何级数)
n 2 n aq a aq aq aq ( a 0) n 0
的收敛性. 解
a aq Sn a aq aq aq ， 1 q a n 收敛 当q 1时, lim q 0 limS n n n 1 q
1 1 1 1 1 1 1 1 (1 ) ( ) ( ) 2 3 2 3 5 2 2n 1 2n 1
1 1 1 (1 ) (n ) , 2 2 2n 1 1 级数收敛 , 且和为 . 2
9
1 例3 讨论级数 ln(1 ) 的敛散性. n n 1
假设调和级数收敛 , 其和为 S.
（S 2 n S n） SS0, 于是 lim n
1 便有 0 ( n ) , 矛盾， 级数发散 . 2
14
性质2 线性运算性质
(1) 如果级数

u
n 1

n 收敛 , 则
kun 亦收敛，且有 n 1

kun k un .
1 1 1 例2 讨论无穷级数 1 3 3 5 ( 2n 1) ( 2n 1) 的收敛性. 1 1 1 1 u ( ), 解 n ( 2n 1)(2n 1) 2 2n 1 2n 1
1 1 1 Sn 1 3 3 5 ( 2n 1) ( 2n 1)
49 . 1 1 6 1 1 3 4
21
1Leabharlann 5例5判断下列级数的敛散性：
100
2. 1 2 3 10
1 n n 1 5

收敛；
1 1 1 1 3. 2 4 6 2n
1 1 2 n 1 n
发散。
22
2 n1
如 果q 1，
n
当q 1时, lim q
n n
lim S n
n
4
发散
如果q 1，
当q 1时,
Sn na
发散
当q 1时, 级数变为a a a a
lim S n不 存 在, 发散
n
综上所述,

2
当 n 时 , 如果级数
S un 的部分和数列
n 1

n
有极限 S ,
即 lim S n S , 则称无穷级数
n
un 收敛,
n 1

这时极限 S 叫做级数
un 的和，并写成
n 1

u
n 1

n
S
如果数列{ S n } 没有极限,则称无穷级数
un 发散.
17
性质4 去掉、添加或改变级数中的有限项,不会影响
它的敛散性(但收敛级数的和可能要改变). 证略。
18
例4 已知
n 1 ( 1 ) un 2 , n 1


u
n1

2 n1
5 , 求 un .
n1

解
由性质3， ( 1)n1 un 2
n 1
(u
如此分析下去,显然阿基里斯离乌龟越来越近,但却是永远
也追不上乌龟的.这个结论显然是错误的,但奇怪的是,这种推理 在逻辑上却没有任何毛病.那么,问题究竟出在哪儿呢？
6
如果我们从级数的角度来分析这个问题,齐诺的这个悖论 就会不攻自破.
设乌龟的速度为 v,则阿基里斯的速度为 10 v,他跑完 1000 米所化


1 解 u n ln(1 ) ln(n 1) ln n , 所以 n
S n ln 2 ln1 ln 3 ln 2 ln(n 1) ln n
ln(n 1) n
所以级数发散.
10
性质1 (级数收敛的必要条件)
若级数
un u1 u2 u3 un n1
级数的部分和

— (常数项)无穷级数
n
S n u1 u2 un ui
部分和数列
i 1
S1 u1 ,
S2 u1 u2 , S3 u1 u2 u3 ,,
Sn u1 u2 un ,
n 1

2 n 1
u2 n ) 2 ,
由性质2，

u
n 1

2n
[u2 n1 ( u2 n1 u2 n )]
n 1

u2 n1 ( u2 n1 u2 n ) 5 2 3 ,
n 1 n 1

所以
(u
n 1

2 n 1
n 0

a 时, 收敛 n 当 | q | 1 1 q aq
当 | q | 1时, 发散
5
公元前五世纪,以诡辩著称的古希腊哲学家齐诺(Zeno) 用他的无穷、连续以及部分和的知识,引发出以下著名的悖论：
如果让阿基里斯(Achilles,古希腊神话中善跑的英雄)和乌 龟之间举行一场赛跑,让乌龟在阿基里斯前头1000米开始,假定 阿基里斯的速度是乌龟的10倍,也永远也追不上乌龟.齐诺的理 论依据是：当比赛开始的时候,阿基里斯跑了1000米,此时乌龟 仍然前于他100米；当阿基里斯跑了下一个100米时,乌龟仍然 前于他10米,…,
n
于是
u
n 1

n
limSn 8 .
n
20
例5
判断下列级数的敛散性：

1 5 1. ( n n ) 4 n0 3
1 解 因为 n , n 0 3


1 n 都收敛， 故原级数收敛， n 0 4

1 5 1 1 且和为 ( n n ) n 5 n 4 n 0 3 n 0 3 n 0 4
u
n1

n
收敛,则必有lim un 0 .
n
证明
un Sn Sn1 ,
n
lim S n S ，
lim un lim( S n S n1 ) lim S n lim S n 1
n n
n n
SS 0.
11
若级数
1 1 1 1 调和级数 1 , 2 3 n n 1 n
1 l i m 0 , 但级数是否收敛 ? n n