当前位置：文档之家 › 幅相频率特性

幅相频率特性

  • 格式：ppt
  • 大小：530.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

控制系统的频率特性

控制系统的频率特性

频率特性是一个复数，有三种表示：
代数式
极坐标式
G j U jV
G( j ) G( j ) G( j ) A( ) ( )
指数式
G( j ) G( j ) e jG ( j ) A( )e j ( )
A G j U 2 V 2
率特性是系统的固有特性，与输入信号无关，
即当输入为非正弦信号时，系统仍然具有自身的频率特性。
频率特性定义为输出量的Fourier变换与输入量
的Fourier变换之比，即
X 0 j G j X i j
频率特性的矢量图
jv V () A () () 0 U () u G(j)
2T 2 1
相频特性 arctan T 一阶惯性环节的幅相频率特性曲 线是一个半圆。
5. 一阶微分环节
频率特性
G j Tj 1
jv
2 45°
幅频特性 A 1 T 2 相频特性 实频特性
∞ ↑ =0 u
arctan T
r为谐振频率
Mr为谐振峰值
r n 1 2 2
M r A max
0.707
1 2 2
2 1 2
7. 二阶微分环节

jv
=0 0 1 u
8. 延迟环节
频率特性
G j e
A 1
jT
1 1 j T

1 TS 1 S j
定义：
A / 1 2T 2 1 稳态输出幅值 A( ) RC网络幅频 2 2 A 输入幅值 1 T 特性
( ) arctan T 稳态输出相位 输入相位 RC网络相频特性

电路的幅频特性和相频特性公式

电路的幅频特性和相频特性公式

电路的幅频特性和相频特性公式幅频特性和相频特性怎么计算幅频特性计算方法:幅频特性=w/(根号下(w平方+1))。

G(jω)称为频率特性，A(ω)是输出信号的幅值与输入信号幅值之比，称为幅频特性。

Φ(ω)是输出信号的相角与输入信号的相角之差，称为相频特性。

相移角度随频率变化的特性叫相频特性。

相频特性=arctan w/0 - arctanw/1=pi/2 - arctanw=arctan 1/w可总结为：相频特性=arctan分子虚部/分子实部-arctan分母虚部/分母实部。

ps:忘了打括号，大家意会就行。

幅频特性计算方法:幅频特性=w/(根号下(w平方+1))可总结为幅频特性=根号下((分子实部平方+分子虚部平方)/(分母实部平方+分母虚部平方))。

频率响应是控制系统对正弦输入信号的稳态正弦响应。

即一个稳定的线性定常系统，在正弦信号的作用下，稳态时输出仍是一个与输入同频率的正弦信号，且稳态输出的幅值与相位是输入正弦信号频率的函数。

在电子技术实践中所遇到的信号往往不是单一频率的, 而是在某一段频率范围内, 在放大电路、滤波电路及谐振电路等几乎所有的电子电路和设备中都含有电抗性元件, 由于它们在各种频率下的电抗值是不相同的, 因而电信号在通过这些电子电路和设备的过程中。

其幅度和相位发生了变化, 亦即是使电信号在传输过程中发生了失真，这种失真有时候是我们需要的, 而有时候是不需要的, 而且必须加以克服。

模电里的幅频特性，和相频特性公式是怎么推导的？通分出来的。

只要会推带电容电导电路的电压比，记住j^2=-1，Z （c）=1/jwc，Z（L）=jwl。

按复数运算规则推就行了。

就是把传递函数的s用jw替掉。

j是虚数单位(和数学上的i一样，工程中习惯用j)，w是正弦信zhi号的角频率。

整个运算的结果是一个复数，这个复数的模就是幅频特性A(w)，复数的辐角就是相频特性fai(w)。

幅频特性是输出正弦信号和输入正弦信号的幅值比，相频特性是输出正弦信号和输入正弦信号的相位差，正的话输出相位比输入相位超前，负的话输出比输入滞后。

信号幅频相频特性的画法(频率响应法)

信号幅频相频特性的画法(频率响应法)

1、频率响应法
•基本思想是把系统中的信号分解为多种不同频率的正弦信号，这些信号经过控制系统时，会以一定的规律产生幅值和相位的变化，通过分析这些
变化规律就能得出关于系统运动的性能指标。

•由于幅值和相位的变化称频率特性函数可以绘制在图形上，因此该方法非常直观。

另外，可以用实验法建立系统的模型，也可以据开环频率特性分析闭环系统的特性。

该方法具有很高的工程价值，深受工程技术人员欢迎。

6 频率响应分析法2
2、频率特性的图示方法
•为了直观地分析系统的特性，通常把幅频和相频特性以图形的形式表示出来：
1.幅相频率特性（奈氏图）
2.对数频率特性（Bode图）
3.对数幅相特性（尼氏图）
6 频率响应分析法5
2.1 幅相频率特性图
•极坐标图：奈奎斯特(Nyquist)图，幅相特性图，当频率连续变化时，频率特性函数在复平面的运动轨迹。

G(jω)=x(ω)+ j y(ω)
ω：0→+∞
6 频率响应分析法6。

自动控制原理--幅相频率特性幅相频率特性(Nyquist图)相关知识

自动控制原理--幅相频率特性幅相频率特性(Nyquist图)相关知识

1
起点
Байду номын сангаас
终点
v 3 v 0
5.2.2 开环系统的幅相频率特性
例7
G1 ( s )
s2 (T1s
K 1)(T2s
1)
G1( j0) 180
G1 G1
G1( j) 0 360
G2 ( s)
K ( s 1)
s2 (T1s 1)(T2s 1)(T3s
1)
G2( j0) 180
G(
j )
1
2 n2
1
j2
n
n
n
1
G
[1
2
2 n
]2
[2
n
]2
2
G arctan
n 2
1 - n2
5.2.1 典型环节的幅相频率特性
谐振频率r 和谐振峰值Mr
G 1
[1
2 n2
]2
[2
n
]2
d G 0
d
d
d
[1
2 n2
]2
[2
n
]2
0
2[1
2 n2
][2(n2
)]
2
[ 2
W( j) K () 0
比例环节的幅相特性 是G平面实轴上的一 个点
5.2幅相频率特性曲线（Nyquist）
5.2.1典型环节的幅相特性曲线 微分环节的幅值与成正比，
2. 微分环节频率特性
相角恒为90度。频率从0→∞
（1）理想微分环节频率特性
幅相特性曲线由G平面原点趋 向虚轴的+j∞处。
① 传递函数 W (s) X c (s) s
n
2
](

第四章 频率特性分析(第9讲)

第四章 频率特性分析(第9讲)
xo (t ) = XiK 1 + T 2ω 2 sin(ωt − arctan Tω )
xo (t ) =
XiK 1+ T ω
2 2
sin(ωt − arctan Tω )
从上式可知，系统的稳态响应的幅值与系统的参数即 比例系数K、时间常数T以及输入谐波的幅值 X i 、频率 ω有关； XiK 幅值 1 + T 2ω 2 相位差
G ( jω ) = Re[G ( jω )] + Im[G ( jω )] = u (ω ) + jv (ω )
G ( jω ) = Re[G ( jω )] + Im[G ( jω )] = u (ω ) + jv (ω )
式中， u (ω ) 是频率特性的实部，称为实频特性， v (ω ) 是频率特性的虚部，称为虚频特性。 显然有：u (ω ) = A(ω ) cos ϕ (ω ),
也是一个复数，可以写成：
G ( jω ) = G ( jω ) e j∠G ( jω ) = A(ω )e jϕ (ω )
因此，传递函数与频率特性的关系为：
G ( jω ) = G ( s ) s = jω
G ( jω ) = G ( s ) s = jω
传递函数的复变量s用jω代替后，传递函数就 变为频率特性。它是传函的特例，是定义在复 平面虚轴上的传递函数。 频率特性的量纲就是传递函数的量纲，也是输 出信号与输入信号的量纲之比。同前面介绍的 微分方程、传递函数、脉冲响应函数等一样， 也是线性控制系统的数学模型。
X iω bm s m + bm −1s m −1 + ⋅⋅⋅ + b1s + b0 X o ( s ) = X i ( s )G ( s ) = 2 ⋅ 2 s + ω an s n + an −1s n −1 + ⋅⋅⋅ + a1s + a0

(完整版)幅相频率特性

(完整版)幅相频率特性

⑹ 振荡环节
G(s)
wn2 s2 2wns wn2
(
s
1
)2 2
s
wn2
1 (s 1)(s 2 )
G(
jw)
1
w2 wn2
G
1
j2 w 1 wn
(1
w2 wn2
)
wn j2 w
wn
(1
w2 wn2
)2
(2
w wn
)2
wn
G( j0) 10 G( j) 0 180
[1
w2 wn2
(ms 1) (Tn s 1)
,
(
n
m)
（1）起点（低频段）：
G(
j0
)H
(
j0
)
lim
w0
(
K jw)v
可得低频段乃氏图：
w 0
（ １ ）
(2)终点（高频段）：此时 w ，这时频率特性与分子分 母多项式阶次之差n m有关。分析可得如下结论：
终点处幅值： lim G ( jω) 0 ω
终点处相角：lim ω
例 系统的幅相曲线如图所试，求传递函数。
K
由曲线形状有
G(s)
s2
wn2
2
s
wn
1
由起点： G( j0) K0 K 2
K
G
[1
w2 w n2
]2
[2
w wn
]2
2 w
G arctan
wn w2
1 - wn2
由(w0)： G( jw0 ) 90 w0 wn 10
由|G(w0)|：
G(w0 )
1 G
1 w2T2 G arctanwT

自动控制原理第5章(2)

自动控制原理第5章(2)

5.2.2 典型环节的奈氏图
控制系统一般是由若干个典型环节所组成。
K ∏ (τ i s + 1)∏ ⎡ (T j s ) 2 + 2ξ jT j s + 1⎤ ⎣ ⎦ ( s ) N ∏ (Tm s + 1)∏ ⎡ (Tk s ) 2 + 2ξ k Tk s + 1⎤ ⎣ ⎦
m =1 k =1 i =1 M j =1 R Q N
以ξ为参变量,计算不同频率ω时的幅值和相角
在极坐标上画出ω由0变 到∞时的矢量端点的轨迹,便 可得到振荡环节的幅相频率 特性(且ζ1＞ζ2)。且振荡环 节与负虚轴的交点频率为 。 ω = 1 = ωn, 幅值为 1
T
2ξ
由奈氏图可知，振荡环节具有相位滞后的作用，输出 滞后于输入的范围为0º→-180º；同时ξ的取值对曲线形状 的影响较大，可分为以下两种情况
绘图方法：当系统或元件的传递函数已知时，可以采 用解析的方法先求取系统的频率特性，再求出系统幅 频特性、相频特性或者实频特性、虚频特性的表达 式，再逐点计算描出奈氏曲线。具体步骤为： 1.求系统或元件的传递函数G（s） 2.用jω代替s，求出频率特性G（jω） 3.求出幅频特性A(ω)与相频特性ϕ（ω）的表达式， 也可求出实频特性与相频特性表达式，并帮助判断 G（jω）所在的象限以确定相角。 4.在0→∞的范围内选取不同的ω，根据A(ω)与ϕ（ω） 表达式计算出对应值，在坐标图上描出对应的向量 G（jω），将所有G（jω）的端点连接描出光滑的 曲线即可得到所求的奈氏曲线。
三、微分环节
理想微分环节的传递函数为 G(s)=s 频率特性为 G(jω)=jω 故幅频特性为 A(ω)=|ω|=ω 与ω成正比。 相频特性为 ϕ (ω)=90º。

自动控制原理 第五章第二节幅相频率特性(上)

自动控制原理 第五章第二节幅相频率特性(上)

（6） 振荡环节
G(s) =
s2
2 n
+
2
n
s
+
2 n
=
(
s
1 )2 + 2
s
=
2 n

+ 1 (s − 1 )(s − 2 )
1
n
n
G(jω)
=
1−
ω2 ωn2
+
j2ξ
ω ωn
G=
1
[1
−
2
2 n
]2
+ [2 2
n
]2
G
=
−arctan
1
−
ωn
2
2 n
G(j0) = 10 G(j) = 0 − 180
5.2 幅相频率特性（Nyquist图）（上）
⑺ 二阶复合微分
G(j ) = 1 − 2
G(s) = T2s2
+ j2
+
2
Ts
+
T=1
1=
n
(
s
n
)
2
+
2
s
n
+1
2 n
n
G=
[1
−
2
2 n
]2
+
[2
n
]2
2
G + = arctan
n 2
1
-
2 n
5.2 幅相频率特性（Nyquist图）（上）
0.707 ( 45)
= 0.707
( = 45) 0 0.707
( 45 90)
=0 ( = 90)

4.2.14.2频率特性的几何表示法

4.2.14.2频率特性的几何表示法

对数频率特性曲线——伯德图
对数相频特性曲线
1 横坐标为的对数lg 分度 2 纵坐标为()
频率每变化十倍，称为十倍频程，记作dec。
对数频率特性曲线——伯德图
对数幅频特性 横坐标表示为：ω 为方便只表示
纵坐标表示为：
L(ω )=20lgA(ω)
L(ω )=20lgA(ω ) dB
40 -20dB/dec
（3）在一张图上绘制低、中、高频段特 性，对系40dB/dec
-1
0
1 lgω
0
0.1
1
10 ω
-20 -40
十倍频程 dec
-20dB/dec
φ (ω )
单位为 dB
0
0.1
1
-90
10 ω
对数相频特性 -180
伯德图的优点
（1）对数运算，将串联环节的幅值相 乘转化为幅值相加的运算
（2）这种方法建立在渐近线的基础上， 简化了幅频特性的绘制过程
频率特性的几何表示法
频率特性法是一种图解分析法，常见的频率 特性曲线有两种：
1 幅相频率特性曲线
2 对数频率特性曲线
幅相频率特性曲线——奈奎斯特曲线（奈氏图）
特点： 以频率ω为变量，将频率特性的幅频特性A(ω)
和相频特性φ(ω)同时表示在复平面上。
Im
= 0 Re
=0
幅相频率特性曲线——奈奎斯特曲线（奈氏图）
作图方法： 取=0和=两点，必要时可在0< < 之间选取
一些特殊点，算出这些点处的幅频值和相频值，然后在 幅相平面上做出这些点，并用光滑的曲线连接起来。
Im
= 0 Re
=0
对数频率特性曲线——伯德图

第五章线性系统的频率分析法

第五章线性系统的频率分析法
5.1 频率特性
一、频率特性的定义： 指线性系统或环节在正弦信号作用下，系统输入
量的频率由0变化到 时，稳态输出量与输入量的振 幅之比和相位差的变化规律，用G(jω) 表示。
xr (t) xrm sin(t)
xc(t) xcm sin(t ( ))
稳态输出量与输入量的频率相同，仅振幅和相位不同。
3）在ω轴上，十倍频程的长度相等；
4）可以将幅值的乘除化为加减L(ω)=20lgA(ω) ；
5）满足直线方程：斜率k
k L(2 ) L(1 ) lg2 lg1
例如：G ( s )
1 Ts
1
的（对数频率特性曲线）伯德图
1）频率特性： G( j ) 1
1
tg1T
jT 1 2T 2 1
微分方程、传递函数、频率特性之间的关系：
s d dt
传递函数
微分方程 系统
d j
dt
频率特性
s j
四、 频率特性的几何表示法
常用频率特性的三种表示法： 1)幅相频率特性曲线（又称：幅相曲线、奈奎斯
特图（Nyquist）、极坐标图） 2)对数频率特性曲线（又称：伯德图 (Bode)）
频率对数分度,幅值/相角线性分度
2）对数频率特性：
0
Bode Diagram
Magnitude (dB)
L( ) 201g 1
-10
T 1 2 2
-20
-30
( ) tg1T
-40 0
Phase (deg)
3）画出伯德图：
-45
-90 10-1
100
101
Frequency (rad/sec)
102
五、典型环节的分解

胡寿松《自动控制原理》(第7版)笔记和课后习题(含考研真题)详解(第5~6章)【圣才出品】

胡寿松《自动控制原理》(第7版)笔记和课后习题(含考研真题)详解(第5~6章)【圣才出品】

第5章线性系统的频域分析法5.1复习笔记本章考点：幅相特性曲线、伯德图的绘制，奈奎斯特稳定判据，稳定裕度计算。

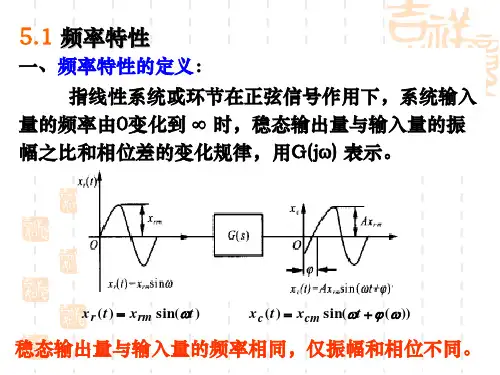
一、频率特性1．定义幅频特性：稳态响应的幅值与输入信号的幅值之比A（ω）。

相频特性：稳态响应与正弦输入信号的相位差φ（ω）。

频率特性：幅频特性和相频特性在复平面上构成的一个完整向量G（jω）＝A（ω）e jφ（ω）。

2．频率特性的几何表示法（重点）（1）幅相频率特性曲线（幅相曲线或极坐标图），横坐标为开环频率特性的实部，纵坐标为虚部， 为参变量。

（2）对数频率特性曲线（伯德图），由对数幅频特性曲线、对数幅相频特性曲线两幅图组成：①对数幅频特性曲线的纵坐标表示L（ω）＝20lgA（ω），单位是分贝，记作dB；②对数相频特性曲线的纵坐标为φ（ω），单位为度“°”。

（3）对数幅相曲线（尼科尔斯图），横坐标表示频率特性的相角φ（ω），纵坐标表示频率特性的幅值的分贝数L（ω）＝20lgA（ω）。

二、典型环节与开环系统的频率特性1．典型环节的频率特性一些主要典型环节的频率特性曲线总结如表5-1-1所示。

表5-1-1典型环节频率特性曲线总结2．开环幅相曲线绘制步骤（1）确定开环幅相曲线的起点（ω＝0＋）和终点（ω＝∞），确定幅值变化与相角变化。

（2）计算开环幅相曲线与实轴的交点。

令Im[G（jωx）H（jωx）]＝0或φ（ωx）＝∠G（jωx）H（jωx）＝kπ（k＝0，±1，…）称ωx为穿越频率，而开环频率特性曲线与实轴交点的坐标值为Re[G（jωx）H（jωx）]＝G（jωx）H（jωx）。

（3）分析开环幅相曲线的变化范围（象限、单调性）。

3．开环对数频率特性曲线绘制步骤（1）开环传递函数典型环节分解并确定一阶环节、二阶环节的交接频率；（2）绘制低频段渐近特性线：在ω＜ωmin频段内，直线斜率为－20vdB/dec；（3）作ω≥ωmin频段渐近特性线，交接频率点处斜率变化表如表5-1-2所示。

5-2频率特性的极坐标图

5-2频率特性的极坐标图
25
极坐标图的形状与系统的型号有关，一般情况如下 （注意起始点）：
II型系统
0
I型系统
0
Im
0
0
Re
0 型系统
26
（1） 0型系统的开环幅相频率特性
① 开环传递函数
m
K( js 1)
G(s)H(s)
j 1 n
，nm
(Tis 1)
i 1
② 频率特性
m
K( j j 1)
G( j)H ( j)
j( jTi 1)
i 1
30
③ 幅相频率特性(奈氏图)绘制
当 0 时
当 时
G( j)H ( j)
K
K
e
j
2
j
即幅值趋于 ，而相角位移为
2
A() 0
() (n m) 90
渐近线与虚轴的距离：
Vx
lim
0
Re[G(
j)H (
j)]
此时Vx是开环增益的函数。
31
当n – m = 4 时， I型系统的奈氏图如下所示：
G( j) G( j1) G( j 2) ……
然后在复平面上找到相应的点，用光滑曲线连起来。
1
（2） 计算
分别计算G(j)的实部和虚部，在复平面上找到相应点，
用光滑曲线连起来。
（3）描点法
找到几个特殊点绘制大致图形
0
| G( j)|0
c
| G( jc )| 1
g
|G( jg )|
G( j)|0 G( jc )
当输入信号的频率ω：0→∞变化时，向量G(jω)的幅值和 相位也随之作相应的变化，其端点在复平面上移动的轨迹称为 极坐标图。

自动控制原理--典型环节的频率特性

自动控制原理--典型环节的频率特性
j
j 1
0j 1
Im
0
Re
0
积分与微分环节
L(dB) 40
积分环节
0
微分环节
40
( )
90
微分环节
0 90
积分环节
20dB / dec
20dB / dec
6
三、微分环节
传递函数: G s s
频率特性:
G(j)
j
ej
π 2
➢1. 幅频特性 A及相频特性
A ,
A
( )
0
1
T
4
2
L,
0
1
T 3dB
4
20lg 2T 2 1
2
近似曲线 精确曲线
对数幅频特性和相频特性：
L() 20 lg 1 (T )2 () tg1 T
0 L0 0
1 L 20 lg 1 3
T
2
4
L
2
L()(dB) 0 0.1 5
10 15 20
0.2
0.3 0.4
0.6 0.8 1
T
2
34
6 8 10
七、一阶不稳定环节
传递函数: G s 1
Ts 1
➢1. 幅相频率特性
频率特性: G j 1
jT 1
G j
1
jT 1
1
1 T2
T
j1 T2
U
jV
U
1 2
2
V
2
1 2
2
一阶不稳定系统的幅相频
率特性是一个为（-1，j0）
为圆心，0.5为半径的半圆。
180O 90O
Im
1

(自动控制原理)幅相频率特性

(自动控制原理)幅相频率特性
相频特性指系统对不同频率输入信号的相位响应。 相位响应可以用于描述信号在系统中的延迟或提前，以及信号的形变情况。 相频特性是分析系统的频率相关性能的重要指标。
相频特性与系统稳定性关系
相频特性的曲线可以显示系统的相位裕度和相位边界。 系统的稳定性与相位裕度有关，较大的相位裕度表示系统对频率变化的抵抗 能力较强。 相频特性可以帮助工程师评估系统的稳定性，并进行相应的调整和改进。
(自动控制原理)幅相频率 特性
幅相频率特性是分析系统对不同频率输入信号的幅度和相位响应的一种方法。
幅频特性解释
幅频特性指系统对不同频率输入信号的幅度响应。 在频率较低时，系统的增益较高，而在频率较高时，系统的增益逐渐降低。 幅频特性的曲线可以绘制成频率响应曲线，可以帮助工程师分析和设计系统。
相频特性解释
幅频特性与系统增益关系
幅频特性的曲线可以显示系统的增益裕度和增益边界。 系统的增益裕度与幅频特性的曲线形态有关，较大的增益裕度表示系统对频 率变化的增益衰减较小。 幅频特性可以帮助工程师评估系统的增益特性，并Байду номын сангаас行相应的控制和调整。
幅频特性应用举例
• 在音响系统中，幅频特性可以帮助调整音量均衡，以使各音频频段的音量适宜。 • 在通信系统中，幅频特性可以帮助调整信号的频率响应，以提高数据传输的可靠性。 • 在电力系统中，幅频特性可以帮助调整电路的频率响应，以优化电力传输和分配。
总结与结论
幅相频率特性是分析系统对不同频率输入信号的幅度和相位响应的重要方法。 通过了解幅频和相频特性，工程师可以评估和优化系统的性能和稳定性。 掌握幅相频率特性的原理和应用，对于理解和设计自动控制系统至关重要。

幅相频率特性图—奈奎斯特Nyquist图

幅相频率特性图—奈奎斯特Nyquist图

第五章频率特性1．本章的教学要求1) 掌握频率特性的基本概念、性质及求取方法；2) 掌握典型环节及系统的频率特性图一奈奎斯特(Nyquist)图的绘制方法；3) 掌握典型环节及系统的对数频率特性图一波德图(Bode)图的绘制方法；4) 使学生掌握频率特性的实验测定法。

5) 使学生掌握奈奎斯特( N yq u i st )稳定性判据应用；6) 掌握对数频率稳定性判据( Bode 判据)应用；7) 掌握相对稳定性的基本概念，相位裕量Y、幅值裕量K g定义、计算、在Nyquist 图与Bode 图上的表示。

2．本章讲授的重点本章讲授的重点是掌握频率特性的基本概念、求取方法；奈奎斯特(Nyquist) 图的绘制方法；波德图(Bode)图的绘制方法；利用频率特性分析控制系统。

3．本章的教学安排本课程预计讲授14 个学时第一讲5.1 频率特性1．主要内容：1) 频率响应和频率特性2) 频率特性的求取方法3) 频率特性的表示方法2．讲授方法及讲授重点：本讲首先给出频率响应定义，用图说明线性系统稳态响应曲线的特点，由此引出幅频特性、相频特性的概念，然后给出频率特性的定义及数学表达式，利用图及公式说明幅频特性、相频特性、实频特性、虚频特性的关系。

在介绍频率特性的求取方法时，首先说明频率特性一般有三种求法：利用定义求取、根据系统的传递函数来求取、通过实验测得。

在此主要说明和推导根据系统的传递函数来求取的方法, 第三种方法后面介绍。

在介绍频率特性的表示方法时，首先说明频率特性的表示方法主要有如下几种：幅频特性和相频特性图、幅相频率特性图、对数频率特性图、对数幅相频率特性图、实频特性图和虚频特性图，分别简单介绍各自特点，然后强调本章重点介绍幅相频率特性(Nyquist) 图和对数频率特性(Bode) 图。

3．教学手段：Powerpoint 课件与黑板讲授相结合。

4．注意事项：在讲授本讲时，频率特性概念比较抽象，同学不好理解，但此概念在本门课中又非常重要，可以联系实际举几个简单例子说明此概念。

第5章线性系统的频域分析法重点与难点一、基本概念1.频率特性的

第5章线性系统的频域分析法重点与难点一、基本概念1.频率特性的

·145·第5章 线性系统的频域分析法重点与难点一、基本概念 1. 频率特性的定义设某稳定的线性定常系统，在正弦信号作用下，系统输出的稳态分量为同频率的正弦函数，其振幅与输入正弦信号的振幅之比)(ωA 称为幅频特性，其相位与输入正弦信号的相位之差)(ωϕ称为相频特性。

系统频率特性与传递函数之间有着以下重要关系：ωωj s s G j G ==|)()(2. 频率特性的几何表示用曲线来表示系统的频率特性，常使用以下几种方法：（1）幅相频率特性曲线：又称奈奎斯特（Nyquist ）曲线或极坐标图。

它是以ω为参变量，以复平面上的矢量表示)(ωj G 的一种方法。

（2）对数频率特性曲线：又称伯德（Bode ）图。

这种方法用两条曲线分别表示幅频特性和相频特性。

横坐标为ω，按常用对数lg ω分度。

对数相频特性的纵坐标表示)(ωϕ，单位为“°”（度）。

而对数幅频特性的纵坐标为)(lg 20)(ωωA L =，单位为dB 。

（3）对数幅相频率特性曲线：又称尼柯尔斯曲线。

该方法以ω为参变量，)(ωϕ为横坐标，)(ωL 为纵坐标。

3. 典型环节的频率特性及最小相位系统 （1）惯性环节：惯性环节的传递函数为11)(+=Ts s G 其频率特性 11)()(+===j T s G j G j s ωωω·146·对数幅频特性 2211lg20)(ωωT L +=(5.1)其渐近线为⎩⎨⎧≥-<=1 )lg(2010)(ωωωωT T T L a (5.2) 在ωT =1处，渐近线与实际幅频特性曲线相差最大，为3dB 。

对数相频特性)(arctg )(ωωϕT -= (5.3)其渐近线为⎪⎩⎪⎨⎧≥︒-<≤+<=10 90101.0 )lg(1.0 0)(ωωωωωϕT T T b a T a (5.4)当ωT =0.1时，有b a b a -=+=1.0lg 0 (5.5)当ωT =10时，有b a b a +=+=︒-10lg 90 (5.6)由式（5.5）、式（5.6）得︒=︒-=45 45b a因此：⎪⎩⎪⎨⎧≥︒-<≤︒-<=10 90101.0 )10lg(451.0 0)(ωωωωωϕT T T T a (5.7)（2）振荡环节：振荡环节的传递函数为10 121)(22<<++=ξξTs S T s G·147·其频率特性)1(21|)()(22ωωξωωT j Ts s G j G j s -+=== 对数幅频特性2222224)1(lg 20)(ωξωωT T L +--= (5.8)其渐近线为⎩⎨⎧≥-<=1)lg(4010)(ωωωωT T T L a (5.9) 当707.0<ξ时，在221ξω-=T 处渐近线与实际幅频特性曲线相差最大，为2121lg20ξξ-。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例 系统的幅相曲线如图所试，求传递函数。 K G ( s ) 由曲线形状有 s2 s 2 1 2 wn wn
由起点：
由(w0)：
G( j 0) K0
K 2
w2 2 w 2 [1 2 ] [2 ] wn wn w 2 wn G arctan w2 1- 2 wn
(1
G( j 0) 10 G( j ) 0 180
w2 2 w [1 2 ] [2 ]2 wn wn w 2 wn G arctan w2 1- 2 wn
§5.2 幅相频率特性 ( Nyquist )（4）
谐振频率wr 和谐振峰值Mr
G 1 [1
15 5(1 j 2w 2 ) j 2 2 (1 w )(1 4w ) w (1 w 2 )(1 4w 2 )
G( j 0) 90 G( j) 0 270
渐近线：
Re [ G( j 0)] 15
与实轴交点：Im[G( jw )] 0 穿越频率 wg 1
1 Ts 1
G
1
1 G ( jw ) 1 jw T
1 w 2T 2 G arctan wT
§5.2 幅相频率特性 ( Nyquist )（2）
⑸ 一阶复合微分
G(s) Ts 1
G( jw ) 1 jwT
G 1 w 2T 2
G arctan wT
求 (w 0) 时实部渐近线 Vx lim Re[G( jw )] w 0 G ( jw不含零点时， ) 3)根据 G ( jw ) 的变化趋势，所在象限和单调性，绘制大概形状。 模值和相位一般会单调收缩，当有零点时，曲线可能会扭曲。
当 1
§5.2.2 系统开环幅相频率特性
例
解
5 ，画G(jw)曲线。 s( s 1)(2 s 1) 5 j 5(1 jw )(1 j 2w ) G( jw ) jw (1 jw )(1 j 2w ) w (1 w 2 )(1 4w 2 ) G( s )
2 0.707 15 10 Re [ G( j 0.707)] (1 0.5)(1 4 0.5) 3
例 G ( s)
k ，画概略开环幅相曲线。 s (Ts 1)
K>0,T>0
G( s)
k (s 1) s 2 (T 1s 1)(T2 s 1)
课程小结
G
K
G( jw0 ) 90
w 0 w n
w0 wn 10

1 3
K 2 由|G(w0)|： G(w0 ) 3 2 2
2 102 G( s) 1 s 2 2 10s 102 3
200 s 2 6.67s 100
§5.2 幅相频率特性 ( Nyquist平面
nm3
对于由最小相位环 节组成的开环系统
v2
K
v0
Re
n m 1
v 1
§5.2
绘制步骤：
幅相频率特性 ( Nyquist )
1)由开环频率特性 G ( jw ) 求出幅频特性 G( jw) 和相频特性G ( jw )，或实 频特性Re[G( jw )]和虚频特性 Im[G( jw )]。 2)求特征点。起点
§5.2
幅相频率特性（Nyquist图）
§5.2.1 典型环节的幅相特性曲线
§5.2.2 开环系统的幅相特性曲线
§5.2 幅相频率特性 ( Nyquist )（3）
§5.2.1 典型环节的幅相频率特性
2 2 1 wn wn ⑹ 振荡环节 G( s ) 2 2 s s s 2wn s w n ( ) 2 2 1 ( s 1 )(s 2 ) wn wn 2
w w ) j 2 2 wn wn 1 G ( jw ) w2 w w2 2 w 2 1 2 j 2 (1 2 ) (2 ) wn wn wn wn 1 G
幅相频率特性（极坐标图）
G( jw ) K G ( jw ) jw
§5.2.1 典型环节的幅相频率特性
⑴ 比例环节
⑵ 微分环节 ⑶ 积分环节 ⑷ 惯性环节
G( s ) K
G( s ) s
1 G( s) s
G( s)
1 G( jw ) jw
G K G 0 G w G 90 G 1 w G 90
. 频率特性
幅频 G( jw ) 相频 G ( jw )
. 幅相特性(Nyquist)
. 对数频率特性(Bode)
对数幅频
. 对数幅相特性(Nichols)
L(w ) 20lgG( jw )
(w ) G( jw )
对数相频
§5.2
§5.2
幅相频率特性 ( Nyquist )（1）
w r w n 1 2 2
M r G ( jw r ) 1 2 1 2
d G 0 dw
d dw
w 2 w 2 ] [ 2 ] 2 wn wn
2
w2 w w 2 2[1 2 ][2( 2 ) ] 2 [ 2 ]( ) 0 wn wn wn wn 4w w2 2 [ 1 2 ] 0 2 2 wn wn

可得低频段乃氏图：
（ １ ）
(2)终点（高频段）：此时 w ，这时频率特性与分子分 母多项式阶次之差n m 有关。分析可得如下结论：
终点处幅值：
ω
lim G ( jω) 0
Im
lim G j ω n m ( ) ( ) 终点处相角： 2 ω
K G( j 0) v(90) v0 v0
终点
nm
G( j) 0 90(n m)
G( jw)] 0 wg Re[G( jwg )] 与负实轴交点：试探，法1 令 Im[
法2 令 G( jw) 180 wg G ( jw g )
§5.2.2 系统开环幅相频率特性（极坐标图）
K ( 1 s 1)( 2 s 1)( m s 1) G ( s) H ( s) v , (n m) s (T1 s 1)(T2 s 1)(Tn s 1)
（1）起点（低频段）：
K G( j 0 ) H ( j 0 ) lim v w 0 ( jw)
自动控制原理
§5. 线性系统的频域分析
§5.1 频率特性的基本概念 §5.2 幅相频率特性（Nyquist图） §5.3 对数频率特性（Bode图） §5.4 频域稳定判据 §5.5 稳定裕度 §5.6 利用开环频率特性分析系统的性能 §5.7 闭环频率特性曲线的绘制
课程回顾
§5.1.2 频率特性 G(jw) 的图解表示方法
w 2 1 2 2 wn
2
w2 2 w 2 [1 ] [ 2 ] 0 2 wn wn
例:当 0.3, wn 1 ，时
wr 1 1 2 0.32 0.9055
Mr 1 2 0.3 1 0.3
2
1.832
§5.2 幅相频率特性 ( Nyquist )（5）