对数幅相图Nichols图

对数幅相图（Nichols图）
对数幅相特性图(Nichols图)是描述系统频率特性的第三种图示方法。

该图纵坐标表示频率特性的对数幅值，以分贝为单位；横坐标表示频率特性的相位角。

对数幅相特性图以频率ω作为参变量，用一条曲线完整地表示了系统的频率特性。

区别于极坐标图的乃氏图，Nichols图的幅值和相角组成直角坐标。

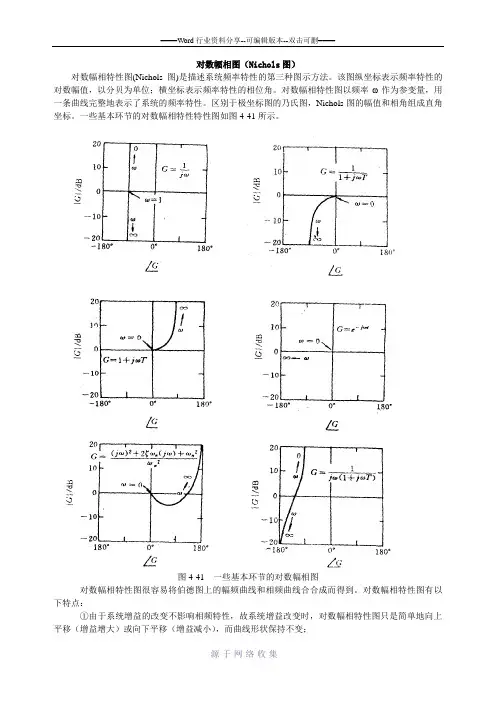
一些基本环节的对数幅相特性特性图如图4-41所示。

图4-41 一些基本环节的对数幅相图
对数幅相特性图很容易将伯德图上的幅频曲线和相频曲线合合成而得到。

对数幅相特性图有以下特点：
①由于系统增益的改变不影响相频特性，故系统增益改变时，对数幅相特性图只是简单地向上平移（增益增大）或向下平移（增益减小），而曲线形状保持不变；
②G（ω）和1／G（jω）的对数幅相特性图相对原点中心对称，即幅值和相位均相差一个符号；
③利用对数相幅特性图，很容易由开环频率特性求闭环频率特性，可方便地用于确定闭环系统的稳定性及解决系统的综合校正问题。

47、传递函数：传递函数是指在零初始条件下，系统输出量的拉式变换与系统输入量的拉式变换之比。

48、系统校正：为了使系统达到我们的要求，给系统加入特定的环节，使系统达到我们的要求，这个过程叫系统校正。

49、主导极点：如果系统闭环极点中有一个极点或者一对复数极点据虚轴最近且附近没有其他闭环零点，则它在响应中起主导作用称为主导极点。

51、状态转移矩阵：()At t e φ=，描述系统从某一初始时刻向任一时刻的转移。

52、峰值时间：系统输出超过稳态值达到第一个峰值所需的时间为峰值时间。

53、动态结构图：把系统中所有环节或者元件的传递函数填在系统原理方块图的方块中，并把相应的输入输出信号分别以拉氏变换来表示从而得到的传递函数方块图就称为动态结构图。

54、根轨迹的渐近线：当开环极点数 n 大于开环零点数 m 时，系统有n-m 条根轨迹终止于 S 平面的无穷远处，且它们交于实轴上的一点，这 n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近线。

55、脉冲传递函数：零初始条件下，输出离散时间信号的z 变换()C z 与输入离散信号的变换()R z 之比，即()()()C z G z R z=。

56、Nyquist 判据（或者奈氏判据）：当ω由-∞变化到+∞时， Nyquist 曲线（极坐标图）逆时针包围（-1，j0）点的圈数N ，等于系统G(s)H(s)位于s 右半平面的极点数P ，即N=P ，则闭环系统稳定；否则（N ≠P ）闭环系统不稳定，且闭环系统位于s 右半平面的极点数Z 为：Z=∣P-N ∣57、程序控制系统: 输入信号是一个已知的函数，系统的控制过程按预定的程序进行，要求被控量能迅速准确地复现输入，这样的自动控制系统称为程序控制系统。

58、稳态误差：对单位负反馈系统，当时间t 趋于无穷大时，系统对输入信号响应的实际值与期望值（即输入量）之差的极限值，称为稳态误差，它反映系统复现输入信号的（稳态）精度。

第五章线性系统的频域分析法5.4 线性系统稳定性分析对数幅相图——Nichols图纵坐标为20lg|G(jω)| ，单位为dB，线性分度。

横坐标为∠G(jω)，单位为度, 线性分度。

Nichols图的绘制过程：先绘制出Bode图，再由其绘制Nichols图。

多用于控制系统校正。

)1)(10(100)(++=s s s s G )1)(11.0(100)(++=s s s s G 例：已知系统开环传递函数为解:(1) 首先将系统开环传递函数写成典型环节串联的形式，即试绘制该系统的开环对数频率特性曲线。

5.4 Nyquist稳定判据和相对稳定性稳定判据：代数判据—Routh判据判断工程实用的图解法判据—Nyquist稳定性判据和Bode图稳定性判据判别系统的稳定性，实际上就是判别系统在S平面右半平面有否闭环极点。

幅角定理设F(S)是复变量S的单值连续解析函数（除S平面上的有限个奇点外）。

S平面上的某一封闭曲线D的内部包含了F(S)的P个极点和Z个零点（包含重根点），且曲线D不通过F(S)任何一个零点和极点。

当S按顺时针方向沿封闭曲线D连续的变化一周时，曲线F(S)在复平面上也按顺时针方向包围原点N=Z-P圈此处定义N为顺时针圈数，即顺时针圈数为正数，逆时针圈数为负数，总圈数为顺时针圈数与逆时针圈数的代数和。

由于系统闭环稳定性与S 平面右半平面中的闭环特征根的数量有关。

故如果选取a)s 平面封闭曲线D 为顺时针包含整个S 平面右半平面的曲线b)F(S)选为F(S)=1+G(s)H(s)()()11()B s F s G(s)H(s)A s =+=+F (s )的极点为开环系统的极点，F (s )的零点为闭环极点则有：有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）假设S平面右半平面包含了F(S)的P个极点和Z个零点，即封闭曲线D包围了F(S)在S右半平面的P个极点和Z个零点根据幅角定理，系统稳定⇒F(S)在S右半平面的零点数Z=0⇒F(S)顺时针包围原点的次数满足N=Z-P=-P。

第三章 系统频率特性系统的时域分析是分析系统的直接方法，比较直观，但离开计算机仿真，分析高阶系统是困难的。

系统频域分析是工程广为应用的系统分析和综合的间接方法。

频率分析不仅可以了解系统频率特性，如截止频率、谐振频率等，而且可以间接了解系统时域特性，如快速性，稳定性等，为分析和设计系统提供更简便更可靠的方法。

本章首先阐明频率响应的特点，给出计算频率响应的方法，接着介绍Nyquist 图和Bode 图的绘制方法、系统的稳定裕度及系统时域性能指标计算。

3.1 频率响应和频率特性3.1.1 一般概念频率响应是指系统对正弦输入的稳态响应。

考虑传递函数为G(s)的线性系统，若输入正弦信号t X t x i i ωsin )(= (3.1-1)根据微分方程解的理论，系统的稳态输出仍然为与输入信号同频率的正弦信号，只是其幅值和相位发生了变化。

输出幅值正比于输入的幅值i X ，而且是输入正弦频率ω的函数。

输出的相位与i X 无关，只与输入信号产生一个相位差ϕ，且也是输入信号频率ω的函数。

即线性系统的稳态输出为)](sin[)()(00ωϕωω+=t X t x (3.1-2)由此可知，输出信号与输入信号的幅值比是ω的函数，称为系统的幅频特性，记为)(ωA 。

输出信号与输入信号相位差也是ω的函数，称为系统的相频特性，记为)(ωϕ。

幅频特性：)()()(0ωωωi X X A = (3.1-3)相频特性：)()()(0ωϕωϕωϕi -= (3.1-4)频率特性是指系统在正弦信号作用下，稳态输出与输入之比对频率的关系特性，可表示为：)()()(0ωωωj X j X j G i = (3.1-5)频率特性)(ωj G 是传递函数)(s G 的一种特殊形式。

任何线性连续时间系统的频率特性都可由系统传递函数中的s 以ωj 代替而求得。

)(ωj G 有三种表示方法：)()()(ωϕωωj e A j G = (3.1-6))()()(ωωωjV U j G += (3.1-7))(sin )()cos()()(ωϕωωωωjA A j G +=(3.1-8) 式中，实频特性：)(cos )()(ωϕωωA U =虚频特性：)()(arctan )()()()()(sin )()(22ωωωϕωωωωϕωωU V V U A A V =+==一般在分析系统的结构及参数变化对系统性能的影响时，频域分析比时域分析要容易些。

1、频率响应法•基本思想是把系统中的信号分解为多种不同频率的正弦信号，这些信号经过控制系统时，会以一定的规律产生幅值和相位的变化，通过分析这些变化规律就能得出关于系统运动的性能指标。

•由于幅值和相位的变化称频率特性函数可以绘制在图形上，因此该方法非常直观。

另外，可以用实验法建立系统的模型，也可以据开环频率特性分析闭环系统的特性。

该方法具有很高的工程价值，深受工程技术人员欢迎。

6 频率响应分析法22、频率特性的图示方法•为了直观地分析系统的特性，通常把幅频和相频特性以图形的形式表示出来：1.幅相频率特性（奈氏图）2.对数频率特性（Bode图）3.对数幅相特性（尼氏图）6 频率响应分析法52.1 幅相频率特性图•极坐标图：奈奎斯特(Nyquist)图，幅相特性图，当频率连续变化时，频率特性函数在复平面的运动轨迹。

G(jω)=x(ω)+ j y(ω)ω：0→+∞6 频率响应分析法62.2 对数频率特性（Bode图）•对数坐标图：伯德(Bode)图，由两辐图组成。

对数幅频特性图+对数相频特性图，横坐标为频率的(以10为底数)对数，单位是10倍频程(dec)。

–对数幅频图的纵坐标为幅频的对数，单位为分贝(dB)–对数相频图的纵坐标为相频值，单位为弧度6 频率响应分析法86 频率响应分析法10伯德(Bode)图的优点•对数坐标图有如下优点：–把乘、除的运算变成加、减运算。

串联环节的Bode 图为单个环节的Bode图迭加。

–K 的变化对应于对数幅频曲线上下移动，而相频曲线不变。

–一张图上可以同时画出低、中、高频的特性。

•因此在工程上得到了广泛的应用6 频率响应分析法112.3 对数幅相特性(尼氏图)对数幅相图•尼科尔斯(Nichols)图，以对数幅频特性为纵坐标（分贝），相频特性为横坐标，频率ω为参变量。

6 频率响应分析法126 频率响应分析法146 频率响应分析法203.7 用Matlab绘制频域特性图•sys = tf(num,den);•伯德图–bode(sys); [mag,phase,w] = bode(sys);•奈奎斯特图–nyquist(sys); [re,im,w] = nyquist(sys);•尼科斯图–nichols(sys); [mag,phase,w] = nichols(sys);6 频率响应分析法23对数频域特性图与频域性能指标分贝对应的频率：截止频率-3分贝对应的频率：带宽6 频率响应分析法5. 开环传递函数的频率特性5.1 开环对数频率特性的绘制①以典型环节的频率特性为依据进行迭加；②首先考虑积分环节和比例环节；③充分利用环节的特征点。