物流数学试题和答案

全国自考（物流数学）模拟试卷2(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．某车间生产四种产品，都要经过A、B两台设备的加工，假定每种产品都必须在设备A上加工完毕后，才能进人设备B，每种商品在每台设备上所需的加工时间如下表所示，问如何安排加工顺序，使总的加工时间最短?正确答案：最小数在第二行第一列，产品1最后加工，划去第一列；剩下的最小数在第一行第四列，先加工产品4，划去第四列；剩下最小数在第二行第三列，产品3倒数第二加工，加工顺序为4，2，3，1．总加工时间为21天，设备B等待3天．2．质点A(7，8)的质量为10克，B(4，一5)的质量为20克，C(一2，6)的质量为30克，求质量中心M的坐标．正确答案：质量中心M的坐标为M(1．5，2．67)．3．货厂现想购进两种货物，甲货物每件重25 kg，体积为1．5m3，乙货物每件重18kg，体积为3．5m3，已知货厂能承受的货物为8600 kg，容积为1000 m3，求最优装配方案．正确答案：设购进甲货物x件，乙货物y件，即最佳方案为购进甲货物200件，购进乙货物200件．4．求x1，x2使其满足约束条件：且使目标函数f(x1，x2)=x1+2x2达到最大．正确答案：画出可行域如图阴影部分所示，目标函数为一组平行向右下方倾斜的直线，当与CD重合时最大．因此，CD 上所有点都为满足条件的x1、x2，最大值，f=x1+2x2=8．5．设某厂自国外进口一部精密仪器，由机器制造厂至出口港有三个港口可供选择，而进口港又有三个可供选择，进口后可经由两个城市到达目的地，其间运输成本如图所示，试求运费最低的路线．机器制造厂→出口港→进口港→城市→某工厂正确答案：起点与终点不同的路线的选择这首先要明确配送中心到产品需求点之间的所有可能的路径，了解路线各连接点的具体位置以及两个相邻连接点之间的运输时间、距离或成本。

然后从配送中心开始计算各条可能路径的累计运输时间、距离或成本．选择数值最小的点作为确定点．重复上述步骤，直到把所有的产品需求点都包括在确定的路线里为止．fk(Sk)表示第是阶段点Sk到E 点的最短距离f1(D1)=30，f1(D2)=40依次类推f1(B1)=110，f2(B3)=80，f3(B2)=70，f1(A)=110，最优决策函数序列之一：A→B2→C1→D1→E 最优决策函数序列之二：A→B3→C1→D1→E 最优决策函数序列之三：A→B3→C2→D2→E6．计算从A到B、C、D的最短路线，已知各路线长度如下所示：正确答案：(1)以fk(Sk)表示第K阶段Sk到A的最短路线，f1(B1)=3，f1(C1)=8，f1(D1)=7 依次类推得f3(B3)=17，f3(C3)=11，f3(D3)=13 f4(B)=16，f4(C)=21，f4(D)=20A→B最优路线：A→B1→C2→C3→B；A→C最优路线：A→B1→C2→C3→C或A→B1→C2→D3→C；A—D最优路线：A→B1→C2→D3→D．7．某城市每年需要从A地运来甲资源，从B地运来乙资源，从C地运来丙资源，各地与该城市中心的距离和各种资源运量如下表所示，求该城市的物流中心的参考坐标M(x，y)．正确答案：物流中心坐标应为M(31．7，41)．8．质点A(4，5)的质量为20 g，B(2，一3)的质量为10 g，C(一1，4)的质量为5 g，求质量中心M的坐标．正确答案：质量中心M坐标为(2．71，2．57)．9．求x1，x2使其满足以下约束条件：且使目标函数f(x1，x2)=一2x1-2x2达到最大．正确答案：可行解域如答下图阴影部分所示，目标函数为一组平行线，经过B点时最大．最优解为x1=1，x2=0，f=一2x1一2x2=一2．10．某钢筋车间，现用的原材料是长度为10 m的钢筋(直径相同)，需要制作一批长度为3 m的钢筋90根，长度为4m的钢筋60根，问怎样建立该问题的数学模型，使原材料最少?正确答案：根据题意，可有如下三种方式：(1)截成3米的3根；(2)截成3米的2根，4米的1根；(3)截成4米的2根．目标函数minf=x1+x2+x3约束条件为：应用题11．配送中心O到A、B、C、D各用户之间的最短距离如下表，用节约法制定最优送货方案．正确答案：路线安排：O→D→B→A→C→O．12．下列交通图中，罔内的数字为某商品的需求量(单位：t)，用小半归邻站法求其最优设场点．正确答案：总需求量为9+4+2+7+6+5+4+3=40(t)，一半为20 t，由小半归邻站法检查端点找最优设场点的过程为E点是最优设场点．13．下列交通图中，圈内的数字为某商品的需求量(单位：t)，用小半归邻站法求其最优设场点．正确答案：总需求量为：3+6+4+7+2+3+4+5+3+2=39(t)，一半为19．5(t)，小半归邻站法检查端点，得C点是最优设场点．14．设有四项加工任务J1、J2、J3、J4，使用机器的顺序是先A后B，所需的时间见下表，问如何安排加工顺序可使加工总时间最短?正确答案：表中最小数在第一行第一列，因此先加工J1，划去第一列；剩下表中最小数在第一行第四列，因此第二个加工J4，划去第四列；剩下表中最小数位于第二行第二列，因此最后加工J2；加工顺序为J1，J4，J3，J2(或J4，J1，J3，J2)．。

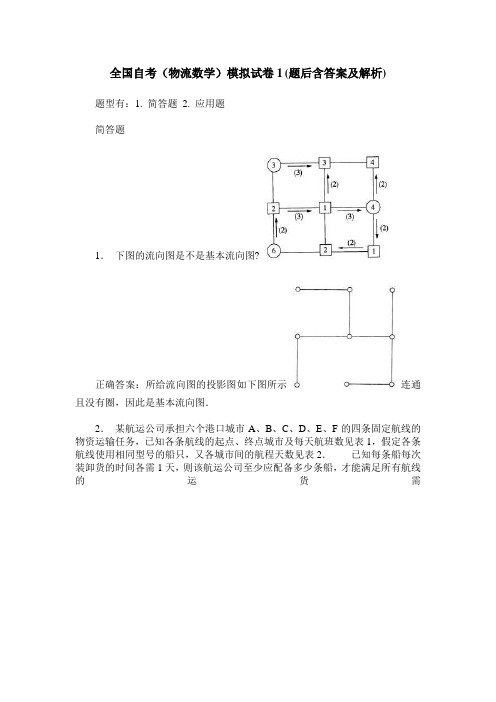
全国自考（物流数学）模拟试卷1(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．下图的流向图是不是基本流向图?正确答案：所给流向图的投影图如下图所示连通且没有圈，因此是基本流向图．2．某航运公司承担六个港口城市A、B、C、D、E、F的四条固定航线的物资运输任务，已知各条航线的起点、终点城市及每天航班数见表1，假定各条航线使用相同型号的船只，又各城市间的航程天数见表2．已知每条船每次装卸货的时间各需1天，则该航运公司至少应配备多少条船，才能满足所有航线的运货需求．正确答案：该公司所需配备船只分两部分：(1)载货航程需要的周转船只数．例如航线1，在港口E装货1天，E→D航程17天，在D卸货1天，总计19天，每天3航班，故该航线周转船只需57条，各条航线周转所需船只数见表3，以上累计共需周转船只数91条．(2)各港口间调度所需船只数，有些港口每天到达船数多于需要船数，例如港口D，每天到达3条，需求1条；而有些港口到达数少于需求数，例如港口B，各港口每天余缺船只数的计算见表4．为使配备船只数最少，应做到周转的空船数为最少，因此建立以下运输问题，其产销平衡表见表5．单位运价表应为相应各港口之间的船只航程天数，见表6．所以，该公司至少配备138条船．3．设效率矩阵为求此指派问题的最小值．正确答案：用匈牙利算法求解：于是最优解(xij)=即原指派问题最优解，最小值fmin=C12+C24+C31+C43+C55=7+6+7+6+6=32．4．某物流公司安排A、B、C、D、E五个人完成J1、J2、J3、J4、J5五项运输任务，每人仅完成一项，已知每人完成各项任务所需的工时定额如下表，求使总耗用工时最低的指派方案．正确答案：对工时矩阵进行变换：最优解为(xij)=即A完成任务J5，B完成任务J3，C完成任务J1，D完成任务J4，E完成任务J2，最低耗时为1+3+3+4+2=13．5．用匈牙利法求解下面指派问题，已知效益矩阵如下：正确答案：于是得(xij)=即最优解为：10+12+15+11=48．6．判断下图是否为基本流向图．正确答案：若一个有n个点的流向图无对流，且它的投影图具有以下性质：(1)连通的；(2)没有圈；(3)有n一1条弧．则这样的流向图称为基本流向图．所给流向图的投影图如下有圈，不是基本流向图．7．判断如图所示流向图是否为基本流向图?若不是，能否用增添虚流向的方法，将它变成基本流向图．正确答案：所给流向图的投影图为不连通，故原图不是基本流向图．增加虚流向得基本流向图8．如图所示流向图是不是基本流向图?正确答案：所给流向图的投影图如下：连通，无圈，是基本流向图．9．某厂有A、B、C三台机器及三项作业Ⅰ、Ⅱ、Ⅲ，要求每台机器只完成一项作业，每项作业只由一台机器完成，三台机器完成各项作业的费用如下表所示：问怎样指派三台机器去完成这三项作业可使费用最小?正确答案：此为三台机器，三项作业问题的指派问题，因此有3!—6种方法．列举如下：(A，B，C)，费用为20+15+12=47，(C，A，B)，费用为30+10+14=54，(B，C，A)，费用为26+19+17=62，(C，B，A)，费用为30+15+17=62，(B，A，C)，费用为26+10+12=48，(A，C，B)，费用为20+19+14=53．所以，由上可知，指派(A，B，C)费用最小，因此最优指派方案为(A，B，C)．10．如图所示交通图的物资调运问题，试作出第一流向图．正确答案：根据“取一端，它的供需归邻站”来作流向图．应用题11．某车场每天有3辆货车经过6个装卸点A1、A2、A3、A4、A5、A6组织巡回运输，在A1点装货需要9个装卸工人，在A2卸货需4个装卸工人，在A3装货需8个装卸工人，在A4卸货需5个装卸工人，在A5装货需5个装卸工人，在A6卸货需要3个装卸工人，如下图所示．试制定合理调配装卸工人的方案．正确答案：调配装卸工人的编号计算法可以用以下四句话概括：车比点多，人往点上搁；车比点少，编号方法好；按点需要人多少，由大到小编编号，车数是几数到几，几个人数跟车跑．此题为车比装卸点少的情况．将所有装卸点按需要装卸工人的数目由多到少排列A1(9人) A3(8人) A4(5人) A5(5人) A2(4人) A6(3人) 车辆数为3，则数到第三个点(5人)，即派5个人跟车，A1需9人，派4个人固定在A1，A3需8人，派3人固定在A3，总共用了3×5+4+3=22个装卸工人．12．下列交通图中，圈内的数字为某商品的需求量(单位：t)，用小半归邻站法求其最优设场点．正确答案：总需求量为：4+7+6+3+5+4+3+3=35(t)，一半为17．5(t) 小半归邻站法D点是最优设场点.13．某工厂生产某种产品的四个配件A、B、C、D都要依次经过甲、乙两台设备加工，假设每种产品都必须在设备甲上加工完毕后，才能进入设备乙加工，每种产品在每台设备上的加工时间(单位：天)如下表所示：问：如何安排这些产品的加工顺序，可以使总的加工时间最短?并求出总的加工时间和设备的等待时间．正确答案：最优安排的简单方法为：排好时间表，从中数最小，属于第一行，应该尽先排，属于第二行，次序往尾排，划掉已排者，剩下照样办．表中最小数3在第二行第一列，因此A最后一个加工，划去第一列；剩下表中最小数4在第二行第四列，因此D倒数第二个加工，划去第四列；剩下表中最小数5在第一行第三列，则第一个加工C；则加工顺序为C、B、D、A．总加工时间为27天，设备乙等待5天．14．求解四个城市旅行推销员问题，其距离矩阵如下表所示，当推销员从1城出发，经过每个城市仅一次，最后回到1城，问按怎样的路线走可使总行程最短?正确答案：由边界条件可知：f0(2，)=d12=8，0(3，)=d13=5，f0(4，)=df14=6，当k=1时，即从1城开始，中间经过一个城市到达i城的最短距离是：f1(2，{3})=f0(3，)+d32=5+9=14，f1(2，{4})=f0(4，)+d42=6+7=13，f1(3，{2})=8+8=16，f1(3，{4})=6+8=14，f1(4，{2})=8+5=16，f1(4，{3})=5+5=10，当k=2时，即从1城开始，中间经过两个城市(它们的顺序随便)到达i城的最短距离是：f2(2，{3，4})=min[f1(3，{4})+d32，f1(4，{3})+d42]=min[14+9，10+7]=17，所以p2(2，{3，4})=4，f1(3，{2，4})=min[13+8，13+8]=2l，所以p1(3，{2，4})=2或4，f2(4，{2，3})=min[14+5，16+5]=19，所以P2(4，{2，3})=2，故k=3时，即从1城开始，中间经过三个城市(顺序随便)回到1城的最短距离是：f1(1，{2，3，4})=min[f2(2，{3，4})+d21，f2(3，{2，4})+d31，f2(4，{2，3})+d41] =min[17+6，21+7，19+9]=23所以p3(1，{2，3，4})=2．由此可知，推销员的最短旅行路线是1—3—4—2—1，最短距离为23．。

全国自考（物流数学）模拟试卷3(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．同时掷三颗骰子，以X表示出现点数的最大值，求E(X)．正确答案：X的分布律为2．某商场每日需要某种货物800件，每批订货费为20元，若每批货物到达后先存入仓库，每月每件的存储费为0．8元，试计算其最佳订货周期．正确答案：c=20(元)，d=0．8(元)，R=800(件)，=0.25，即每1/4月订购一批．3．盒中装有5个球，其中有3个白球，2个黄球，从中任取一球，取后不放回，设A表示“第1次取到的是白球”，B表示“第二次取到的是白球”，求条件概率P(B｜A)．正确答案：4．求x1，x2使其满足约束条件：且使目标函数f(x1，x2)=4x1一2x2达到最大．正确答案：可行域为空，因此没有可行解．5．水果店要订购一批草莓，由于草莓会在短期内腐坏；所以必须决定合适的订购数量，每单位草莓的成本为5元，售价8元，订购成本可忽略不计，短期内未卖出的草莓便腐坏不可再销售，短期内周边居民对草莓的需求量可能有三种情况：60(单位)，70(单位)，90(单位)．若订货量只能为10的倍数，试用算术平均准则确定该批发商应订购多少单位草莓?正确答案：由题意得损益值表应订购70单位草莓，可使收益的算术平均值最大．6．求解如图所示网络的中国邮路问题．(用添弧的方法，▲为邮局)正确答案：7．有甲、乙两种货物，甲货物每件重5 kg，体积为0．01m3；乙货物每件重1 kg，体积为0．001m3，汽车载重量为2．5 t，有效容积为4m3，求最优配装方案．正确答案：设装甲货物x件，乙货物y件，则有即最优配装方案是甲货物装300件，乙货物装1000件．8．假设某厂计划生产甲、乙两种产品，其主要材料有钢材4吨，铜材3吨，专用设备能力8千台时，材料与设备能力的消耗定额及单位商品所获利润如表所示．正确答案：目标函数maxS=2x1+2x2约束条件为9．某公司经销某种商品，该商品由3个生产点A1、A2、A3生产，日产量为A1=60吨，A2=40吨，A3=60吨，分别销往4个销售点B1、B2、B3、B4，各销地日销量为B1=30吨，B2=50吨，B3=40吨，B4=40吨．已知每吨产品从各生产点到各销售地的运价如表所示．问应如何建立模型，保证产销平衡且总运费最小?正确答案：目标函数为minS=5x11+6x12+10x13+3x14+4x21+x22+9x23+7x24+4x31+2x32+3x33+8x34约束条件为10．计算从A到E的最短路线图，已知各路线图如下所示．正确答案：(k=1，2，3，4) k=4时，f4(D1)=3，f4(D2)=4，即从A到E的最短路线为A→B3→C2→D2→E，最短路线长度为11．应用题11．设某光学仪器厂制造的透镜，第一次落下时打破的概率为1/2，若第一次落下未打破，第二次落下打破的概率为7/10，若前两次落下未打破，第三次落下打破的概率为9/10，试求透镜落下三次而未打破的概率．正确答案：以Ai(i=1，2，3)表示事件“透镜第i次落下打破”，以B表示事件“透镜落下三次而未打破”，因为B=故有另解，按题意而是两两互不相容的事件，故有12．在某种产品的零件加工中，零件Ⅰ在甲、乙、丙三种机床上都能加工，零件Ⅱ在甲、乙、丙三种机床上也全能够加工，每个产品仅由一个零件Ⅰ和一个零件Ⅱ组成．每种零件的产量是：一个工作日中，甲种机床能够生产出10个零件Ⅰ或者20个零件Ⅱ；乙种机床能够生产出20个零件Ⅰ或30个零件Ⅱ；丙种机床能够生产出30个零件Ⅰ或80个零件Ⅱ，现在甲种机床3台，乙种机床3台，丙种机床1台，试求在一个工作日里，怎样分配这些机床的工作，可使成套产品达到最多?正确答案：甲、乙、丙三个车床的牛产效率列表如下：丙生产零件Ⅱ的效率最高，乙生产零件Ⅰ的效率最高，故乙生产零件Ⅰ，丙生严零件Ⅱ．设甲生产零件Ⅰx个，零件Ⅱy个，有解得x=26，y=6分配方案为可得成套产品86套．13．配送中心O到A、B、C、D各用户之间的最短距离如下表：用节约法制定最优送货方案．正确答案：路线安排：O→B→A→D→C→O．14．下列交通图中，圈内的数字为某商品的需求量(单位：t)，用小半归邻站法求基最优设场点．正确答案：总需求量为：4+6+7+5+3+3+2=30(t)，一半为15(t) ．由小半归邻站法检查端点找最优设场点的过程为：B点是最优设场点．。

物流数据测试题及答案1. 物流数据的采集方式有哪些？A. 手动记录B. 自动采集C. 网络传输D. 以上都是答案：D2. 物流数据中，货物重量的单位通常是什么？A. 千克B. 吨C. 磅D. 克答案：A3. 物流数据中，货物体积的计算公式是什么？A. 长×宽×高B. 长+宽+高C. 长÷宽÷高D. 长-宽-高答案：A4. 物流数据中，货物追踪的常用技术是什么？A. GPSB. RFIDC. 条形码D. 以上都是答案：D5. 物流数据中，货物运输时间的计算方法是什么？A. 出发时间+运输时间B. 出发时间-到达时间C. 到达时间-出发时间D. 出发时间÷运输时间答案：C6. 物流数据中，货物损坏率的计算公式是什么？A. 损坏货物数÷总货物数×100%B. 总货物数÷损坏货物数×100%C. 损坏货物数×总货物数÷100%D. 总货物数×损坏货物数÷100%答案：A7. 物流数据中，货物周转率的计算公式是什么？A. 总货物数÷平均库存量B. 平均库存量÷总货物数C. 总货物数×平均库存量÷100%D. 平均库存量×总货物数÷100%答案：A8. 物流数据中，货物运输成本的计算包括哪些因素？A. 燃料费B. 人工费C. 车辆折旧费D. 以上都是答案：D9. 物流数据中，货物运输效率的衡量指标是什么？A. 货物运输时间B. 货物运输成本C. 货物周转率D. 货物损坏率答案：C10. 物流数据中，货物库存管理的目标是什么？A. 最大化库存量B. 最小化库存成本C. 最大化库存周转率D. 最小化库存周转率答案：B结束语：以上物流数据测试题及答案旨在帮助考生更好地理解和掌握物流数据的相关知识，希望考生能够通过这些题目加深对物流数据重要性的认识，并在实际工作中有效应用。

物流数学练习题答案1. 计算某物流公司在一个月内运输货物的总成本。

已知每运输一吨货物的成本为100元，该月共运输了500吨货物。

答案：总成本为50000元。

2. 确定某物流中心的货物存储容量。

已知物流中心有10个仓库，每个仓库的存储容量为1000立方米。

答案：总存储容量为10000立方米。

3. 计算物流公司在运输过程中的货物损耗率。

已知运输的货物总量为1000吨，损耗量为10吨。

答案：损耗率为1%。

4. 确定物流公司在一个月内运输货物的平均速度。

已知该月共运输了2000公里，运输时间为10天。

答案：平均速度为200公里/天。

5. 计算物流公司在一个月内运输货物的总重量。

已知每辆卡车的载重量为5吨，该月共运输了100辆卡车。

答案：总重量为500吨。

6. 确定物流公司在一个月内运输货物的总体积。

已知每辆卡车的载货体积为20立方米，该月共运输了50辆卡车。

答案：总体积为1000立方米。

7. 计算物流公司在一个月内运输货物的总费用。

已知每运输一吨货物的费用为150元，该月共运输了300吨货物。

答案：总费用为45000元。

8. 确定物流公司在一个月内运输货物的平均成本。

已知总成本为60000元，运输的货物总量为400吨。

答案：平均成本为150元/吨。

9. 计算物流公司在一个月内运输货物的总距离。

已知每辆卡车的行驶距离为1000公里，该月共运输了50辆卡车。

答案：总距离为50000公里。

10. 确定物流公司在一个月内运输货物的总时间。

已知每辆卡车的运输时间为5天，该月共运输了30辆卡车。

答案：总时间为150天。

全国自考（物流数学）模拟试卷4(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．随机变量X～N(1，4)，求P{0＜X≤1．6}．(已知(0．3)=0．6179，(0．5)= 0．6915)正确答案：P{0＜X≤1.6}==0.6179-(1-0.6915)=0.30942．某批发商要准备一批某种商品在节日期间销售，由于短期内只能一次订货，所以必须决定订货的数量，每单位商品购入成本为3元，售8元，订购成本可忽略不计，未出售的商品只能作处理品，每单位按1元处理．节日期间对该商品的需求量可能有三种情况：50(单位)、80(单位)、120(单位)，若订货量只能为10的倍数，试用算术平均准则确定该批发商应订购多少单位该商品．正确答案：益损值=8×销售量一3×订购量+1×处理品数量由题意得益损值表订货量为50时，益损值的算术平均值为×(250+250+250)=250 订购量为80时，益损值的算术平均值为×(190+400+400)=330 订购量为120时，益损值的算术平均值为×(110+320+600)≈343．33 由于订购量为120时收益的算术平均值最大．所以批发商应订购120单位该商品．3．某饲养场养动物，设每头动物每天至少需要700 g蛋白质，30 g矿物质，100 mg维生素，现有五种饲料可供选用，各种饲料每公斤营养成分含量及单价如下所示：试建立数学模型，既满足动物生长的营养要求，又使费用最省的选择饲养方案．正确答案：设五种饲料分别选取x1、x2、x3、x4、x5g，则得下面的数学模型MinZ=0．2x1+0．7x2+0．4x3+0．3x4+0．8x54．将下图中的最优投递路线用添弧的方法找出来．(▲为邮局)正确答案：选择最优投递路线的方法可以概括为三句话：先为奇偶点，奇点对对连；连线不重叠，重叠要改变；圈上连线长，不得过半圈．5．一班的数学成绩平均分为74分，标准差为9；二班的数学成绩平均分为73分，标准差为6．问哪一个班的数学成绩差异大?正确答案：变异系数定义为V=×100％，即标准差与平均数的比值，表示数据相对于其平均数的分散程度．V1=×100％=×100％=12．16％；V2=×100％=×100％=8．22％；故一班成绩差异大．6．有两种灌装工艺需要考察，从中各抽取10个成品，测得它们的质量如下表(单位：k)根据以上数据分别求出两种工艺的平均质量和方差，并指出哪种工艺更稳定．正确答案：工艺A的平均质量：工艺B的平均质量：因此，工艺A更稳定．7．A、B、C、D四城市间距离表如下求从某一城市出发遍历各城市各一次的最短路径．正确答案：匈牙利算法思路(1)距离矩阵的各行分别减去该行的最小数；各列也分别减去该列的最小数．(2)求最优路径：①从第一行开始依次检查，找出只有一个0元素没有加标记的行．给这个0元素加标记“*”，与这个加标记的“0*”同列的0元素全划去，重复此过程，直到每一行没有未加标记的0元素或者至少有两个未加标记的0元素．②从第一列开始依次检查各列，找出只有一个未加标记的0元素的列，将这个0元素加上标记“*”，并将与这个“0*”同行的0元素划去，重复此过程，直到每一列没有尚未加标记的0元素或者至少有两个未加标记的0元素．③重复①，②两个步骤，直到表中没有未加标记的0元素为止．用匈牙利算法求解D2中有四个“0*”，得路径A→C→D→B→A，最短路径总长为4+5+4+6=19·8．已知X～N(μ，σ2)，Y～N(一μ，)，Z～N(0，)，x、y、z相互独立，且P{X＜0)=0．2，求P{μ＜5X+4Y一3Z＜7μ)．正确答案：由于x，y，z相互独立且都服从正态分布，所以5X+4Y一3Z～N(μ，36σ2)，由于0．2=P{X＜0)=所求9．点A(2，5)质量为15 g，B(3，一1)质量为12 g，C(一2，3)质量为3 g，求质量中心M的坐标．正确答案：质量中心M坐标为(2，2.4)·10．某车场每天有3辆车经过6个装卸点A1、A2、A3、A4、A5、A6，在A1装货需5人，在A2卸货需7人，在A3装货需8人，在A4卸货需10人，在A5装货需9人，在A6卸货需4人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按需要人数由多到少排列如下：A4(10人) A5(9人) A3(8人) A2(7人) A1(5人) A6(4人) 从人数多的一端数到第3点A3(8人)，即派8人跟车，A4点再派2人，A5点再派1人，其余各点不派人．共需8×3+2+1=27(人)．应用题11．甲公司发明了一种新的家电设备，并拥有专利权，该公司对该产品今后三年的回报进行了研究，认为该产品未来的销售如果好的话，三年中的利润将为120万元，如果销售一般，三年的利润为50万元，如果销售较差，三年的亏损将为15万元，另有一家公司乙愿意购买该产品的专利权，并根据产品的销售状况支付报酬，如果销售情况好，甲公司的收益将为80万元，如果销售一般，收益将为32万元，如果销售较差，收益将为10万元，具体数据如下表：试用最大收益期望原则判断哪种方案最优．正确答案：最大收益期望原则方案一的收益期望为：0．2×120+0．5×50一0．3×15=44．5(万元) 方案二的收益期望为：0．2×80+0．5×32+0．3×10=35(万元)，应选择收益期望最大的方案，因此选择方案一．12．由某机器厂生产的螺栓长度(cm)服从参数μ=10．05，σ=0．06的正态分布，规定长度在范围10．050．12内为合格品，求一螺栓为不合格品的概率．((2)=0．9772)正确答案：13．某物品的需求量前四期分别为65 kg，80 kg，110 kg，135 kg，试用简单算术平均法对第五期的需求量进行预测．正确答案：设Di(i=1,2,3,4)表示第i周的实际需求量．用Ft表示第i周的需求量的预测值，则有F5=(D1+D2+D3+D4)=×(65+80+110+135)=97．5(kg)．14．某车站12h内平均有48辆车驶过，每辆车停留只有10 min，每停留一次只能上一名乘客，求其到达率、服务率、平均稠密度．正确答案：到达率为λ=48/12=4(人／h)，服务率为μ=×60=6(人／h)。

全国自考（物流数学）模拟试卷9(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．质点A(2，5)的质量为20g，B(3，一3)的质量为12g，C(一4，2)的质量为8g．求质量中心M的坐标．正确答案：即质量中心M坐标为(1，1，2)．2．有7个球，其中3个红球，4个白球，每次只取一个，直到取出白球为止(不放回取球)，求在取到白球之前取到红球的个数的概率分布，并计算其期望．正确答案：设X表示“在取到白球之前取到红球的个数”，Ak表示“第k次抽到的是白球”X=0，1，2，3，列表如下：3．有甲、乙两种货物，甲货物每件重5kg，体积为0．001m3，乙货物每件重10kg，体积为0．004m3．货车的载重量为15t，容量为5m3，求最佳配装方案．正确答案：设装甲货物x件，乙货物y件最佳配装方案为货车装甲货物1000件，乙货物1000件．4．有甲、乙两种货物，甲货物每件重26 kg，体积为0．02m3，乙货物每件重3 kg，体积为0．01m3，汽车载重量为4 t，有效容积为5m3．求最优配装方案·正确答案：设装甲货物x件，装乙货物y件，则有最佳配装方案是装甲货物125件，乙货物250件．5．从两个班英语试卷中抽出8份，其成绩如下表(单位：分)根据以上数据分别求出两个班的平均成绩和方差，并指出哪个班成绩较稳定·正确答案：一班平均成绩：(92+83+60+77+58+89+90+70)=77.375二班平均成绩：(78+82+69+85+81+77+80+75)=78.375一班成绩的方差：=158.984二班成绩的方差：=22.0144 由此可得二班的成绩更稳定．6．判断下图是不是基本流向图．若不是，改为基本流向图．正确答案：所给流向图投影如下：此图连通，仅有一个需要检查的圈ABED，且圈长为3+3+2+2=10，内圈流向长为2+3≤10/2=5，同样外圈流向也为5≤5，因此流向图是最优的，也是基本流向图．7．用添弧的方法找出下图中邮递员的最优投递线．(▲代表邮局)正确答案：如下图所示：8．某纺织厂生产四种花色的棉布A、B、C、D，每种棉布依次经过甲、乙两台机器进行染色，且必须在设备甲加工完后才能进入设备乙，各种棉布在甲、乙设备上加工时间(单位：分钟)如下表所示．问：如何安排棉布的加工顺序，可使总加工时间最短?并求出总的加工时间和设备的等待时间．正确答案：表中最小数7在第一行第二列，因此先加工棉布B，划去第二列；剩下表中最小数11，位于第一行第三列，因此第二个加工棉布C，划去第三列；剩下表中最小数12，位于第二行第一列，因此棉布A最后加工；加工顺序BCDA，总加工时间为61分钟，设备乙空闲11分钟．9．某厂用6种化工原料混合配制某工业材料，要求配制成的每份工业材料内含成分A不少于9单位/公斤，成分B不少于15单位/公斤，有关数据如表所示，问应如何建立该问题数学模型，既满足对A、B的质量要求，又使配制成本最低?正确答案：目标函数为minf=38x1+32x2+31x3+27x4+22x5+19x6约束条件为10．有两个化肥厂A1、A2，存储化肥数量分别为800 t和1000 t，现将这些化肥运到三个市场B1、B2、B3去出售，各市场需求量分别为300 t、950 t、650 t．已知各化肥厂到各市场的单位运费如下表试建立该问题的数学模型，使总运费最省．正确答案：物资调运的数学模型相当于下列数学问题：设有m+n个正数：a1,a2,…am；b1,b2,…bn 满足条件又给出mn个非负的数cij(i=1，2，…，m；j=1，2，…，n)，求mn个变数xij(i=1，2，…，m；J=1，2，…，n)的值，使其满足约束条件：且xij≥0 (i=1，2，…，m；j=1，2，…，n)，并使目标函数达到最小值(或最大值) 设从化肥厂Ai运往市场Bj的数量为xij吨(i=1，2，j=1，2，3)，则目标函数为minS=8x11+7x12+5x13+4x21+6x22+10x23 约束条件为应用题11．某车场每天有3辆车经过5个装卸点A1、A2、A3、A4、A5，在A1装货需7个工人，在A2卸货需6个工人，在A3装货需5人，在A4卸货需8人，在A5装货需9人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按要求人数由多到少排列如下：A5(9人) A4(8人) A1(7人) A2(6人) A3(5人) 从人数多的一端数到第3点，A1(7人)，故派7人跟车。

附录习题参考答案 第1章一、判断题1．√；2．×；3. √二、选择题1．B ；2．C ；3．D ；4．C第2章一、判断题1．√；2．√；3.×；4.×；5．√；6.×。

二、选择题1．C ；2．A ；3．B ；4．B ；5．C ；6．A ；7．A ；8．C ；9．A ；10．D ；11．D ；12．A ；13．D ；14．B ；15．C三、计算题1．（1）14*,4,221===z x x 。

（2）无界解。

（3）无穷多最优解，66*=z 。

（4）无可行解。

2．（1）无界解。

（2）3/44*,3/4,3/1121===z x x 。

（3）25*,0,5,15321====z x x x 。

（4）无穷多最优解。

47*,7,4/9,2/11321====z x x x 是其中之一。

（5）2/33*,2,2/3,1321====z x x x 。

（6）3/11*,0,3/4,3/1321====z x x x 。

3．（1）29/184*,29/43,0,29/2321====z x x x 。

（2）5*,1,0,0321====z x x x 。

（3）5/52*,0,5/4,5/4321====z x x x 。

（4）无可行解。

（5）4/7*,4/3,4/7,0321====z x x x 。

（6）无可行解。

（7）5*,1,0,2321====z x x x 。

4．（1）3218y 15y 5y wmin ++-=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤=+--≥-+≤-+≥+无约束， 32132132132131y 0y ,0y 77y y 2y -4y 5y y 35y 4y 4y 3y y - （2）32141711max y y y w ++=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤=+--≤++-=-≥-+0,07621544312434332132132131321y y y y y y y y y y y y y y 无约束，（3）43217y 12y 3y -5y w max ++=⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≥++=-+-≥++-≤-+0y 0y ,y 55y y -4y y 3y 4y y -2y 2y 2y 2y 32y y 3y 324143214324321321，无约束，y（4）432112y 9y 5y -17y w min ++=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≥≥+=++-≥-+≤-+无约束，，，342143214321321421y 0y 0y 0y 7y -6y -4y 3y -2y 25y y 44y 2y -3y y 2y y y（5）43217y 12y 3y 5y w max ++-=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-=+--≤-+≤-+--≥++无约束42314321421432321y ,0y 0,y ,y 55y y 4y y 3y y 2y 3y 2y 2y 22y 3y y （6）43217y 25y 3y 12y w min ++-=⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≤++-≥-+-≤++--=-+无约束42314214324321321y ,0y ,0y ,y 75y 4y y 1y 4y y 12y 2y 2y 2y 32y 3y y 5．（1）43212263min y y y y w +++=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤++≤++≤+≤++0,,,636283432132143221421y y y y y y y y y y y y y y y （2）)1,0,0,0,0,1,2,2(*=Y6．（1）最优解为T X )0,0,0,5/16,5/28(*=，最优值为5/332=z 。

全国自考（物流数学）模拟试卷10(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．10件产品中有4件次品，现逐个进行检查，求不连续出现2个次品的概率．正确答案：记A为“不连续出现2个次品”，A发生等价于从6个正品之间的5个空档加上首尾两个空当，总共7个空当中随意诜出4个放上次品，排法有×4!，正品排列方法有61种．不连续出现2个次品的慨率为：2．货厂现欲购进两种货物，甲货物每件重50 kg，体积为3m3，乙货物每件重36 kg，体积为7 m3，已知货厂能承受重物8600 kg，容积为1000 m3，求最优装配方案．正确答案：设购进甲货物x件，乙货物y件，则有即最佳方案为购进甲货物100件，购进乙货物100件．3．某货运站每年需向工厂运送货物，各工厂与该货运站的距离和每年的送货量如下表所示，求该货运站的参考地理位置坐标(x，y)．正确答案：所以，该货运站应在坐标为M(28，30)的位置．4．某车场每天有2辆货车经过4个装卸点A1、A2、A3、A4，在A1点卸货需4人，在A2点卸货需7人，在A3点卸货需9人，在A4点卸货需5人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将4个装卸点按需要人数由多到少排列如下：A3(9人) A2(7人) A1(5人) A4(4人) 从人数多的一端数到第2点．A2为7人，故派7人跟车，A3派2人，其余各点不派人，共需7×2+2=16(人)．5．设有三个产地A1、A2、A3、A4生产某种物资，四个销地B1、B2、B3、B4需要该种物资，各产地的产量和销地的销量以及各产地运往各销地的单位运价如表所示：试建立该问题的数学模型，使总运费最省．正确答案：目标函数为minS=2x11+9x12+10x13+7x14+x21+3x22+4x23+2x24+8x31+4x32+2x33+5x34约束条件为6．某车场每天有4辆货车经过6个装卸点A1、A2、A3、A4、A5、A6，在A1装货需11个工人，在A2卸货需6人，在A3卸货需7人，在A4卸货需5人，在A5卸货需4人，在A6卸货需8人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按需要人数由多到少排列如下：A1(11人) A6(8人) A3(7人) A2(6人) A4(5人) A5(4人) 从人数多的一端数到第4点，A2(6人)，故派6人跟车，A1再派5人，A2点再派2人，A3点再派1人，其余各点不派人，即共需6×4+5+2+1=32(人)．7．用一个仪器测量杆子5次得下列数：92，94，103，105，106(以毫米计算)，求杆子长度的样本均值及仪器误差的方差．正确答案：样本平均值：(92+94+103+105+106)=500/5=100 方差：8．某车场每天有3辆货车经过4个装卸点A1、A2、A3、A4，在A1卸货需9人，在A2装货需7人，在A3卸货需10人，在A4卸货需5人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按需要人数由多到少排列如下：A3(10人) A1(9人) A2(7人) A4(5人) 从人数最多的一端数到第3点，A2(7人)，故派7人跟车，A3点再派3人，A1点再派2人，其余各点不派人，这样，共需装卸工7×3+3+2=26(人)．9．某车间有甲、乙、丙三人及三项任务Ⅰ、Ⅱ、Ⅲ，要求每人只完成一项任务，每项任务只由一人完成，三人完成各项任务的费用如下：问怎样指派三人去完成这三项任务，可使费用最小?正确答案：三人三项任务，共3!=6种指派方法，列举如下：(甲，乙．丙)．费用为13+11+3=27，(丙，甲，乙)．费用为10+8+5=23，(乙，丙，甲)．费用为5+6+7=18，(丙，乙，甲)．费用为10+11+7=28，(乙，甲，丙)．费用为5+8=3=16，(甲，丙，乙)．费用为13+6+5=24，由上可知，(乙，甲，丙)费用最小，即最优指派方案为(乙，甲，丙)．10．制作玻璃的过程中有甲、乙两道关键工艺，所有作品都必须依次经历甲、乙两工艺，现有A、B、C、D四作品，其在甲、乙工艺的时间如下表所示(单位：小时)．问：如何安排加工顺序，可使总时间最短?并求出总的加工时间和设备的等待时间．正确答案：表中最小数3在第一行第一列，因此先加丁产品A，划去第一列；剩下表中最小数4，位于第一行第二列，因此第2个加工产品B，划去第二列；剩下表中最小数5，位于第二行第三列，因此产品C最后加工．加工顺序为ABDC，总加工时间为31小时，乙工艺等待6小时．应用题11．有某种物资17万吨，由A1、A2、A3、A4发出，发量分别为5，2，3，7(万吨)，运往B1、B2、B3、B4，收量分别为8、1、3、5(万吨)，收发量是平衡的，它的交通图如下所示，问应如何调运，才使运输量(吨公里)最小?正确答案：调运方式如图所示：12．有4个工人，需指派他们分别完成4项工作，每人做各项工作所消耗的时间如下表：问如何指派4人可使总耗时最小?正确答案：对矩阵进行变换调整后得指派矩阵如下：即甲→A 乙→D 丙→C 丁→B 或甲→B乙→A 丙→C 丁→D．13．已知运输问题的供需求关系与单位运价如下表所示，求使总运费最省的调运方案．正确答案：①计算初始方案②计算检验数，均为正数，即为最优方案此时运费35×3+25×2十15×2+25×5+20×2十15×3=395．14．某物流公司安排甲、乙、丙、丁四人完成A、B、C、D四项运输任务，每个仅完成一项，已知每人完成各项任务所需的工时定额如下表，求使总耗用工时最低的指派方案．正确答案：于是得到最优解(xij)=即甲完成任务B，乙完成任务A。

一、选择题（每题3分，共30分）1. 下列哪个单位表示货物的重量？（）A. 公里B. 吨C. 米D. 秒答案：B2. 下列哪个概念不属于物流的基本职能？（）A. 运输B. 存储C. 包装D. 营销答案：D3. 物流中的“最后一公里”指的是？（）A. 从仓库到配送中心的距离B. 从配送中心到终端客户的距离C. 从生产地到仓库的距离D. 从客户到供应商的距离答案：B4. 下列哪种物流方式属于直达运输？（）A. 公路运输B. 铁路运输C. 水路运输D. 航空运输答案：A5. 物流过程中的库存管理主要目的是？（）A. 降低运输成本B. 减少货物损失C. 优化库存水平D. 提高生产效率答案：C6. 下列哪种物流模式属于第三方物流？（）A. 企业自营物流B. 第四方物流C. 供应链物流D. 自有物流答案：A7. 物流信息化建设的关键技术不包括？（）A. GPS定位技术B. 条形码技术C. 人工智能技术D. 红外线技术答案：D8. 下列哪种物流设备不属于自动化物流设备？（）A. 自动分拣机B. 自动输送线C. 机器人D. 纸箱答案：D9. 下列哪种物流服务不属于增值服务？（）A. 包装服务B. 仓储服务C. 装卸服务D. 金融服务答案：D10. 物流成本核算的核心指标是？（）A. 运输成本B. 仓储成本C. 整体物流成本D. 单位成本答案：C二、填空题（每题2分，共20分）11. 物流的五大基本职能是：运输、存储、包装、装卸和______。

答案：流通加工12. 物流活动中的“三流”是指：物流、______和资金流。

答案：信息流13. 物流信息化建设的三个阶段是：自动化、______和智能化。

答案：网络化14. 物流成本核算的基本原则是：谁受益、谁承担。

答案：成本效益15. 物流管理中的“JIT”是指：______。

答案：及时制16. 物流服务中的“COSCO”是一家著名的______。

答案：集装箱运输公司17. 物流设备中的“AGV”是指：______。