物流数学试题

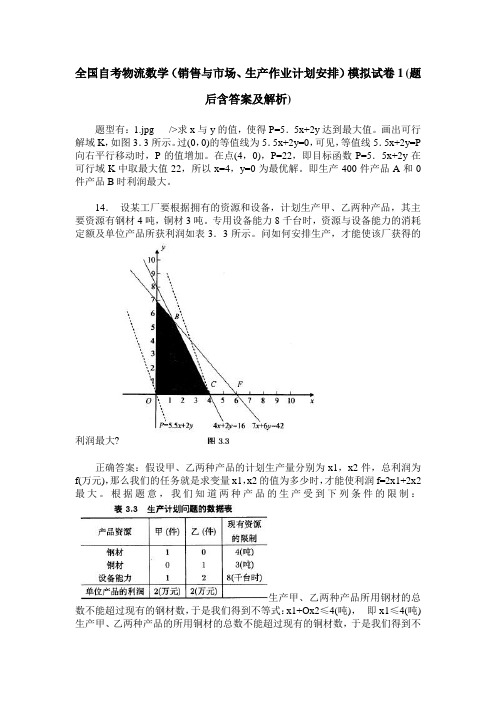
全国自考物流数学（销售与市场、生产作业计划安排）模拟试卷1(题后含答案及解析)题型有：1.jpg />求x与y的值，使得P=5．5x+2y达到最大值。

画出可行解域K，如图3．3所示。

过(0，0)的等值线为5．5x+2y=0，可见，等值线5．5x+2y=P 向右平行移动时，P的值增加。

在点(4，0)，P=22，即目标函数P=5．5x+2y在可行域K中取最大值22，所以x=4，y=0为最优解。

即生产400件产品A和0件产品B时利润最大。

14．设某工厂要根据拥有的资源和设备，计划生产甲、乙两种产品，其主要资源有钢材4吨，铜材3吨。

专用设备能力8千台时，资源与设备能力的消耗定额及单位产品所获利润如表3．3所示。

问如何安排生产，才能使该厂获得的利润最大?正确答案：假设甲、乙两种产品的计划生产量分别为x1，x2件，总利润为f(万元)，那么我们的任务就是求变量x1，x2的值为多少时，才能使利润f=2x1+2x2最大。

根据题意，我们知道两种产品的生产受到下列条件的限制：生产甲、乙两种产品所用钢材的总数不能超过现有的钢材数，于是我们得到不等式：x1+Ox2≤4(吨)，即x1≤4(吨)生产甲、乙两种产品的所用铜材的总数不能超过现有的铜材数，于是我们得到不等式：Ox1+x2≤3(吨)，即x2≤3(吨)生产甲、乙两种产品所用的设备能力总数不能超过现有设备能力的台时数，于是我们得到不等式：x1+2x2≤8(千台时)综合上述讨论，在加工时间和利润与产品产量成线性关系的假设下，考虑到甲、乙两种产品的生产量不能为负数，即x1，x2≥0，于是最优方案写成线性规划的数学模型为：建立x1Ox2直角坐标系，求满足线性规划问题约束条件的可行域，如图3．4所示。

平行向右移动直线f，可知，的值是增加的。

同时，由可以得到C点的坐标为(4，2)。

当f增加到C点时，x1=4，x2=2，maxf=2×4+2×2=12即甲产品生产量为4件，乙产品生产量为2件时，总利润f达到最大值12(万元)。

物流师计算题（物流师考试复习专用）1.采购物资200t，甲报价320元/吨，运费5元/吨，订购费用200元；乙报价300元/吨，运费30元/吨，订购费用500元。

计算哪个供应商成本低？2.第一次第二次第三次第四次第五次采购吨数70 60 60 70 60使用天数8 8 7 10 7该物资每吨50元，保管费用为存货价值的20%，订购成本为100元/吨，订购提前期5天，安全储备量40吨，求最佳订购批量（360天/年）；订购点的库存最小的TC；存货平均占用多少资金？3.月份 1 2 3 4 5 6 7需求量11 10 9 12 11 10 11平均值请用短序移动平均法（组距取3）来预测8月份的需求量4.需求量100吨/周，进货单价250元/吨，补货启动费用500元/次，存储费率为单价的30%，求经济批量，基本经济补货周期，（设1年52.14周）5.自行配送成本与外车配送成本之和100000元，自车次配送成本500元，配送延迟车次数50次，求配送延迟率。

6.位置坐标配送量1 （325.75）15002 （400，150）2503 （450，350）4504 （350，400）3505 （25，450）4507.仓库8400件显示器到库，单件尺寸60cm*60cm*60cm，重50公斤，外包装上表示堆码极限为6，问需要为此货物准备多大的货位？其储存定额多大？若该批货物放在使用面积650平方米的仓库中，仓库面积利用率和存放该物资的有效面积多大？8.20箱物品，每箱价格1000元，日维持库存费用为售价的1%配送方案配送成本成本隔夜10002天7004天5009.1一个月内配送货物100000立方米，车辆总体积5000立方米，配送车辆运转率为80%，计算车辆满载率。

10.某轮从大连港装载0.5m3鹿茸运至汉堡港，托运人提供的CIF 价格为USD 45000.00，货物保险费率为3%，请计算应收取的全程运费是多少？11.设由天津港运往莫桑比克首都马普托门500箱，每箱体积为0.025立方米，毛重为30千克。

物流数学试题分章汇编（5361）一、数学预备知识06．41. 设有10个球,其中有3个白球,7 个黑球,随机地从中取两个球,每取一次就要把球放回,求所抽取的两个球颜色相同的概率。

Φ(1)=0.84132. 若随机变量X—N(3, 22), 求P(2＜X≤5) 。

已知7. 从两个班数学试卷中各抽出8份,其成绩如下表(单位:分)根据以上数据分别求出两个班的平均成绩和方差,并指出哪个班的成绩更稳定。

07．41．(本题4分)已知＝1，求x的值．3．(本题5分)写出题3图所示的图的关联矩阵M和相邻矩阵A，并指出图中哪些点是奇点．2007年7月2008．42008年7月1．(小题4分)在题1图所示的图中，有多少个奇点？有多少条弧？2．(本题6分)数据集{2,3,5,4,3，3，1}，求(1)极差R；(2)方差σ2。

3．(本题6分)设随机变量X的概率分布为：求：(1)常数a；(2)随机变量X的数学期望E(X)。

2009．42009年7月2010年4月2、（本题6分）写出题2图所示图的关联矩阵和相邻矩阵。

题2图3、（本题6分）计算数据：2.3.4.4.5.6的平均数和方差。

2010年7月1．(本题5分)随机变量x服从正态分布N(4，32)，求P(一2≤x≤4)。

已知Φ0(2)=0.9772。

3．(本题6分)从某班数学考试的试卷中抽出5份，其成绩分别为：62，86，79，65，83。

计算这5份试卷的平均成绩和方差。

2011年4月1、（本题5分）随机变量X服从正态分布N（-3,24），求P（-1≤X≤1）。

已知中0 （1）=0.8413。

2、（本题6分）某月我国铁路、公路、水路和航空货运量为（单位：万吨）2.50 12.46 2.04 31.13求这四种运输方式的平均货运量和标准差（结果保留四位小数）。

2011年7月1．(本题5分)题1图中共有多少个奇点?多少条弧?2．(本题5分)某月我国铁路、公路、水路和航空总客运量为(单位：亿人)0．92 16．89 0．22 0．12求：这四种运输方式的平均客运量及标准差。

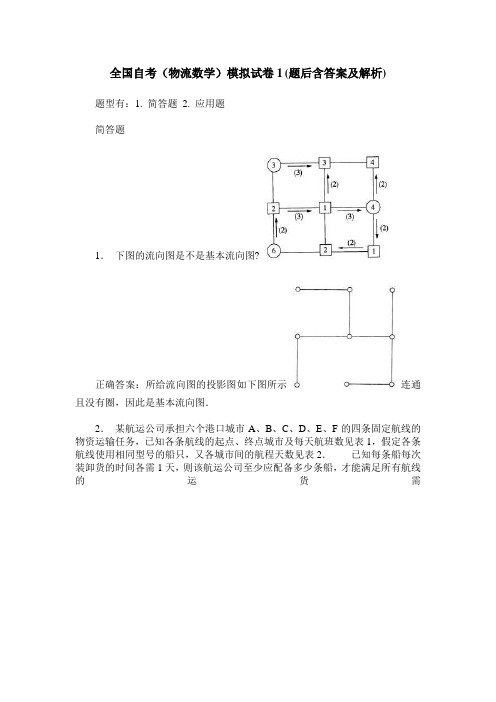
全国自考（物流数学）模拟试卷1(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．下图的流向图是不是基本流向图?正确答案：所给流向图的投影图如下图所示连通且没有圈，因此是基本流向图．2．某航运公司承担六个港口城市A、B、C、D、E、F的四条固定航线的物资运输任务，已知各条航线的起点、终点城市及每天航班数见表1，假定各条航线使用相同型号的船只，又各城市间的航程天数见表2．已知每条船每次装卸货的时间各需1天，则该航运公司至少应配备多少条船，才能满足所有航线的运货需求．正确答案：该公司所需配备船只分两部分：(1)载货航程需要的周转船只数．例如航线1，在港口E装货1天，E→D航程17天，在D卸货1天，总计19天，每天3航班，故该航线周转船只需57条，各条航线周转所需船只数见表3，以上累计共需周转船只数91条．(2)各港口间调度所需船只数，有些港口每天到达船数多于需要船数，例如港口D，每天到达3条，需求1条；而有些港口到达数少于需求数，例如港口B，各港口每天余缺船只数的计算见表4．为使配备船只数最少，应做到周转的空船数为最少，因此建立以下运输问题，其产销平衡表见表5．单位运价表应为相应各港口之间的船只航程天数，见表6．所以，该公司至少配备138条船．3．设效率矩阵为求此指派问题的最小值．正确答案：用匈牙利算法求解：于是最优解(xij)=即原指派问题最优解，最小值fmin=C12+C24+C31+C43+C55=7+6+7+6+6=32．4．某物流公司安排A、B、C、D、E五个人完成J1、J2、J3、J4、J5五项运输任务，每人仅完成一项，已知每人完成各项任务所需的工时定额如下表，求使总耗用工时最低的指派方案．正确答案：对工时矩阵进行变换：最优解为(xij)=即A完成任务J5，B完成任务J3，C完成任务J1，D完成任务J4，E完成任务J2，最低耗时为1+3+3+4+2=13．5．用匈牙利法求解下面指派问题，已知效益矩阵如下：正确答案：于是得(xij)=即最优解为：10+12+15+11=48．6．判断下图是否为基本流向图．正确答案：若一个有n个点的流向图无对流，且它的投影图具有以下性质：(1)连通的；(2)没有圈；(3)有n一1条弧．则这样的流向图称为基本流向图．所给流向图的投影图如下有圈，不是基本流向图．7．判断如图所示流向图是否为基本流向图?若不是，能否用增添虚流向的方法，将它变成基本流向图．正确答案：所给流向图的投影图为不连通，故原图不是基本流向图．增加虚流向得基本流向图8．如图所示流向图是不是基本流向图?正确答案：所给流向图的投影图如下：连通，无圈，是基本流向图．9．某厂有A、B、C三台机器及三项作业Ⅰ、Ⅱ、Ⅲ，要求每台机器只完成一项作业，每项作业只由一台机器完成，三台机器完成各项作业的费用如下表所示：问怎样指派三台机器去完成这三项作业可使费用最小?正确答案：此为三台机器，三项作业问题的指派问题，因此有3!—6种方法．列举如下：(A，B，C)，费用为20+15+12=47，(C，A，B)，费用为30+10+14=54，(B，C，A)，费用为26+19+17=62，(C，B，A)，费用为30+15+17=62，(B，A，C)，费用为26+10+12=48，(A，C，B)，费用为20+19+14=53．所以，由上可知，指派(A，B，C)费用最小，因此最优指派方案为(A，B，C)．10．如图所示交通图的物资调运问题，试作出第一流向图．正确答案：根据“取一端，它的供需归邻站”来作流向图．应用题11．某车场每天有3辆货车经过6个装卸点A1、A2、A3、A4、A5、A6组织巡回运输，在A1点装货需要9个装卸工人，在A2卸货需4个装卸工人，在A3装货需8个装卸工人，在A4卸货需5个装卸工人，在A5装货需5个装卸工人，在A6卸货需要3个装卸工人，如下图所示．试制定合理调配装卸工人的方案．正确答案：调配装卸工人的编号计算法可以用以下四句话概括：车比点多，人往点上搁；车比点少，编号方法好；按点需要人多少，由大到小编编号，车数是几数到几，几个人数跟车跑．此题为车比装卸点少的情况．将所有装卸点按需要装卸工人的数目由多到少排列A1(9人) A3(8人) A4(5人) A5(5人) A2(4人) A6(3人) 车辆数为3，则数到第三个点(5人)，即派5个人跟车，A1需9人，派4个人固定在A1，A3需8人，派3人固定在A3，总共用了3×5+4+3=22个装卸工人．12．下列交通图中，圈内的数字为某商品的需求量(单位：t)，用小半归邻站法求其最优设场点．正确答案：总需求量为：4+7+6+3+5+4+3+3=35(t)，一半为17．5(t) 小半归邻站法D点是最优设场点.13．某工厂生产某种产品的四个配件A、B、C、D都要依次经过甲、乙两台设备加工，假设每种产品都必须在设备甲上加工完毕后，才能进入设备乙加工，每种产品在每台设备上的加工时间(单位：天)如下表所示：问：如何安排这些产品的加工顺序，可以使总的加工时间最短?并求出总的加工时间和设备的等待时间．正确答案：最优安排的简单方法为：排好时间表，从中数最小，属于第一行，应该尽先排，属于第二行，次序往尾排，划掉已排者，剩下照样办．表中最小数3在第二行第一列，因此A最后一个加工，划去第一列；剩下表中最小数4在第二行第四列，因此D倒数第二个加工，划去第四列；剩下表中最小数5在第一行第三列，则第一个加工C；则加工顺序为C、B、D、A．总加工时间为27天，设备乙等待5天．14．求解四个城市旅行推销员问题，其距离矩阵如下表所示，当推销员从1城出发，经过每个城市仅一次，最后回到1城，问按怎样的路线走可使总行程最短?正确答案：由边界条件可知：f0(2，)=d12=8，0(3，)=d13=5，f0(4，)=df14=6，当k=1时，即从1城开始，中间经过一个城市到达i城的最短距离是：f1(2，{3})=f0(3，)+d32=5+9=14，f1(2，{4})=f0(4，)+d42=6+7=13，f1(3，{2})=8+8=16，f1(3，{4})=6+8=14，f1(4，{2})=8+5=16，f1(4，{3})=5+5=10，当k=2时，即从1城开始，中间经过两个城市(它们的顺序随便)到达i城的最短距离是：f2(2，{3，4})=min[f1(3，{4})+d32，f1(4，{3})+d42]=min[14+9，10+7]=17，所以p2(2，{3，4})=4，f1(3，{2，4})=min[13+8，13+8]=2l，所以p1(3，{2，4})=2或4，f2(4，{2，3})=min[14+5，16+5]=19，所以P2(4，{2，3})=2，故k=3时，即从1城开始，中间经过三个城市(顺序随便)回到1城的最短距离是：f1(1，{2，3，4})=min[f2(2，{3，4})+d21，f2(3，{2，4})+d31，f2(4，{2，3})+d41] =min[17+6，21+7，19+9]=23所以p3(1，{2，3，4})=2．由此可知，推销员的最短旅行路线是1—3—4—2—1，最短距离为23．。

物流数学练习题答案1. 计算某物流公司在一个月内运输货物的总成本。

已知每运输一吨货物的成本为100元，该月共运输了500吨货物。

答案：总成本为50000元。

2. 确定某物流中心的货物存储容量。

已知物流中心有10个仓库，每个仓库的存储容量为1000立方米。

答案：总存储容量为10000立方米。

3. 计算物流公司在运输过程中的货物损耗率。

已知运输的货物总量为1000吨，损耗量为10吨。

答案：损耗率为1%。

4. 确定物流公司在一个月内运输货物的平均速度。

已知该月共运输了2000公里，运输时间为10天。

答案：平均速度为200公里/天。

5. 计算物流公司在一个月内运输货物的总重量。

已知每辆卡车的载重量为5吨，该月共运输了100辆卡车。

答案：总重量为500吨。

6. 确定物流公司在一个月内运输货物的总体积。

已知每辆卡车的载货体积为20立方米，该月共运输了50辆卡车。

答案：总体积为1000立方米。

7. 计算物流公司在一个月内运输货物的总费用。

已知每运输一吨货物的费用为150元，该月共运输了300吨货物。

答案：总费用为45000元。

8. 确定物流公司在一个月内运输货物的平均成本。

已知总成本为60000元，运输的货物总量为400吨。

答案：平均成本为150元/吨。

9. 计算物流公司在一个月内运输货物的总距离。

已知每辆卡车的行驶距离为1000公里，该月共运输了50辆卡车。

答案：总距离为50000公里。

10. 确定物流公司在一个月内运输货物的总时间。

已知每辆卡车的运输时间为5天，该月共运输了30辆卡车。

答案：总时间为150天。

一、库存控制问题2、求经济定购量和再订购点，已知：年需求量D=1000单位/年；日平均需求量d，=1000/365 储存单位物资的储存费K=1.25元/(件·年)；每次订货的订货费C=5元/次；提前订货时间L=5天；物品单价P=12.50元；问订购批量EOQ、再订购点ROL和年总成本TC。

3、某电子商务企业每年需要购买8000套儿童服装，每套儿童服装的单价为100元，其年储存成本为3元，每次的订购成本为是30元。

问：最优订货数量、年订购次数和预期每次订货间隔时间各为多少？（一年以360天计）4、某电子商务企业计划对它的最畅销商品进行库存分析。

这种商品的年需求量为10000件，单价为100元，年储存成本率约为单价的20%。

该企业的每次订货成本是100元，平均交货时间为10天。

问：经济订货数量是多少？一年的订货次数为多少？两次订货的间隔时间是多少天？年库存总成本是多少？5、某单位2003年某物资每单位物资的价格为100元，单位物资产生的年持有成本为其价值的25%，单次订货费用为100元/次，通过预测，预计2004年该类物资的总需求量为1800单位。

若2004年单位物资价格、持有成本和单次订货费维持在2003年水平，请计算出2004年的经济订购批量、订货周期。

6、某金属公司销售钢材，过去12周，每周销售的钢材分别是162、173、167、180、181、172、170、168、167、174、170和168吨。

如果它们服从正态分布，订货进货提前期为1周，一次订货费用200元，1吨钢材保管1周需要保管费10元，要求库存满足率达到90%。

如果实行定量订货法控制，应该怎样进行操作？7、某商场以前各个月的电视机销售量是随机变化的，大概服从正态分布，平均值为50台，变化范围为±10台。

电视机订货进货提前期从正态分布，平均值为5天，变化范围为±1天，商场希望库存满足率达到95%，则商场实施定量订货法的订货点应取多少合适？8、某公司为了制定定量订货法订货策略，特意统计了某种物资的订货提前期的销售量。

全国自考（物流数学）模拟试卷10(题后含答案及解析) 题型有：1. 简答题 2. 应用题简答题1．10件产品中有4件次品，现逐个进行检查，求不连续出现2个次品的概率．正确答案：记A为“不连续出现2个次品”，A发生等价于从6个正品之间的5个空档加上首尾两个空当，总共7个空当中随意诜出4个放上次品，排法有×4!，正品排列方法有61种．不连续出现2个次品的慨率为：2．货厂现欲购进两种货物，甲货物每件重50 kg，体积为3m3，乙货物每件重36 kg，体积为7 m3，已知货厂能承受重物8600 kg，容积为1000 m3，求最优装配方案．正确答案：设购进甲货物x件，乙货物y件，则有即最佳方案为购进甲货物100件，购进乙货物100件．3．某货运站每年需向工厂运送货物，各工厂与该货运站的距离和每年的送货量如下表所示，求该货运站的参考地理位置坐标(x，y)．正确答案：所以，该货运站应在坐标为M(28，30)的位置．4．某车场每天有2辆货车经过4个装卸点A1、A2、A3、A4，在A1点卸货需4人，在A2点卸货需7人，在A3点卸货需9人，在A4点卸货需5人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将4个装卸点按需要人数由多到少排列如下：A3(9人) A2(7人) A1(5人) A4(4人) 从人数多的一端数到第2点．A2为7人，故派7人跟车，A3派2人，其余各点不派人，共需7×2+2=16(人)．5．设有三个产地A1、A2、A3、A4生产某种物资，四个销地B1、B2、B3、B4需要该种物资，各产地的产量和销地的销量以及各产地运往各销地的单位运价如表所示：试建立该问题的数学模型，使总运费最省．正确答案：目标函数为minS=2x11+9x12+10x13+7x14+x21+3x22+4x23+2x24+8x31+4x32+2x33+5x34约束条件为6．某车场每天有4辆货车经过6个装卸点A1、A2、A3、A4、A5、A6，在A1装货需11个工人，在A2卸货需6人，在A3卸货需7人，在A4卸货需5人，在A5卸货需4人，在A6卸货需8人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按需要人数由多到少排列如下：A1(11人) A6(8人) A3(7人) A2(6人) A4(5人) A5(4人) 从人数多的一端数到第4点，A2(6人)，故派6人跟车，A1再派5人，A2点再派2人，A3点再派1人，其余各点不派人，即共需6×4+5+2+1=32(人)．7．用一个仪器测量杆子5次得下列数：92，94，103，105，106(以毫米计算)，求杆子长度的样本均值及仪器误差的方差．正确答案：样本平均值：(92+94+103+105+106)=500/5=100 方差：8．某车场每天有3辆货车经过4个装卸点A1、A2、A3、A4，在A1卸货需9人，在A2装货需7人，在A3卸货需10人，在A4卸货需5人．问：怎样调配装卸工人最合理?正确答案：车比装卸点少，将所有装卸点按需要人数由多到少排列如下：A3(10人) A1(9人) A2(7人) A4(5人) 从人数最多的一端数到第3点，A2(7人)，故派7人跟车，A3点再派3人，A1点再派2人，其余各点不派人，这样，共需装卸工7×3+3+2=26(人)．9．某车间有甲、乙、丙三人及三项任务Ⅰ、Ⅱ、Ⅲ，要求每人只完成一项任务，每项任务只由一人完成，三人完成各项任务的费用如下：问怎样指派三人去完成这三项任务，可使费用最小?正确答案：三人三项任务，共3!=6种指派方法，列举如下：(甲，乙．丙)．费用为13+11+3=27，(丙，甲，乙)．费用为10+8+5=23，(乙，丙，甲)．费用为5+6+7=18，(丙，乙，甲)．费用为10+11+7=28，(乙，甲，丙)．费用为5+8=3=16，(甲，丙，乙)．费用为13+6+5=24，由上可知，(乙，甲，丙)费用最小，即最优指派方案为(乙，甲，丙)．10．制作玻璃的过程中有甲、乙两道关键工艺，所有作品都必须依次经历甲、乙两工艺，现有A、B、C、D四作品，其在甲、乙工艺的时间如下表所示(单位：小时)．问：如何安排加工顺序，可使总时间最短?并求出总的加工时间和设备的等待时间．正确答案：表中最小数3在第一行第一列，因此先加丁产品A，划去第一列；剩下表中最小数4，位于第一行第二列，因此第2个加工产品B，划去第二列；剩下表中最小数5，位于第二行第三列，因此产品C最后加工．加工顺序为ABDC，总加工时间为31小时，乙工艺等待6小时．应用题11．有某种物资17万吨，由A1、A2、A3、A4发出，发量分别为5，2，3，7(万吨)，运往B1、B2、B3、B4，收量分别为8、1、3、5(万吨)，收发量是平衡的，它的交通图如下所示，问应如何调运，才使运输量(吨公里)最小?正确答案：调运方式如图所示：12．有4个工人，需指派他们分别完成4项工作，每人做各项工作所消耗的时间如下表：问如何指派4人可使总耗时最小?正确答案：对矩阵进行变换调整后得指派矩阵如下：即甲→A 乙→D 丙→C 丁→B 或甲→B乙→A 丙→C 丁→D．13．已知运输问题的供需求关系与单位运价如下表所示，求使总运费最省的调运方案．正确答案：①计算初始方案②计算检验数，均为正数，即为最优方案此时运费35×3+25×2十15×2+25×5+20×2十15×3=395．14．某物流公司安排甲、乙、丙、丁四人完成A、B、C、D四项运输任务，每个仅完成一项，已知每人完成各项任务所需的工时定额如下表，求使总耗用工时最低的指派方案．正确答案：于是得到最优解(xij)=即甲完成任务B，乙完成任务A。

一、选择题（每题3分，共30分）1. 下列哪个单位表示货物的重量？（）A. 公里B. 吨C. 米D. 秒答案：B2. 下列哪个概念不属于物流的基本职能？（）A. 运输B. 存储C. 包装D. 营销答案：D3. 物流中的“最后一公里”指的是？（）A. 从仓库到配送中心的距离B. 从配送中心到终端客户的距离C. 从生产地到仓库的距离D. 从客户到供应商的距离答案：B4. 下列哪种物流方式属于直达运输？（）A. 公路运输B. 铁路运输C. 水路运输D. 航空运输答案：A5. 物流过程中的库存管理主要目的是？（）A. 降低运输成本B. 减少货物损失C. 优化库存水平D. 提高生产效率答案：C6. 下列哪种物流模式属于第三方物流？（）A. 企业自营物流B. 第四方物流C. 供应链物流D. 自有物流答案：A7. 物流信息化建设的关键技术不包括？（）A. GPS定位技术B. 条形码技术C. 人工智能技术D. 红外线技术答案：D8. 下列哪种物流设备不属于自动化物流设备？（）A. 自动分拣机B. 自动输送线C. 机器人D. 纸箱答案：D9. 下列哪种物流服务不属于增值服务？（）A. 包装服务B. 仓储服务C. 装卸服务D. 金融服务答案：D10. 物流成本核算的核心指标是？（）A. 运输成本B. 仓储成本C. 整体物流成本D. 单位成本答案：C二、填空题（每题2分，共20分）11. 物流的五大基本职能是：运输、存储、包装、装卸和______。

答案：流通加工12. 物流活动中的“三流”是指：物流、______和资金流。

答案：信息流13. 物流信息化建设的三个阶段是：自动化、______和智能化。

答案：网络化14. 物流成本核算的基本原则是：谁受益、谁承担。

答案：成本效益15. 物流管理中的“JIT”是指：______。

答案：及时制16. 物流服务中的“COSCO”是一家著名的______。

答案：集装箱运输公司17. 物流设备中的“AGV”是指：______。

2022年4月物流数学试题参考答案-图文课程代码一、简答题(本大题共11小题,共54分)1.设有10个球,其中有3个白球,7个黑球,随机地从中取两个球,每取一次就要把球放回,求所抽取的两个球颜色相同的概率。

2.若随机变量某—N(3,22),求P(2＜某≤5)已知Φ0(1)=0.84133.某超市每月需要某种货物6000件,每批订货费为30元,每次货物到达后先存人仓库,每月每件存储费为0.25元。

试求最优订购批量及平均每月的总费用。

4.某物流园区每年需要从A地运来铸铁,从B地运来煤炭,从C地运来各种造型材料,从D地运来钢材,各地与该城市中心的距离和每年的材料运量如下表所示,求设置该物流园区的参考位置的坐标M(某,y)。

距离、运量表原材料供应地及其坐标距离中心20坐标距离(h)年运输量(t)200012001000250070606020205020ABCD某1y1某2y2某3y3某4y45.不计算,用添弧的方法找出题5图中邮递员的最优投递路线,(▲代表邮局)题5图题6图6.题6图的流向图是不是基本流向图若不是,试将其改造为基本流向图。

7.从两个班数学试卷中各抽出8份,其成绩如下表(单位:分)一班成绩(某i)二班成绩(yi)62858063697190727081756885657870根据以上数据分别求出两个班的平均成绩和方差,并指出哪个班的成绩更稳定。

8.某批发商要准备一批某种商品在节日期间销售,由于短期内只能一次订货,所以他必须决定订货的数量,每单位商品购入成本为3元,售价8元,订购成本可忽略不计。

未售出的商品只能作处理品,每单位按1元处理。

节日期间用户对该商品的需求量可能有三种情况:40(单位),70(单位),120(单位)。

若订货量只能为10的倍数,试用算术平均准则确定该批发商应订购多少单位该商品。

9.某车间生产四种产品A1、A2、A3、A4,每种产品都要依次经过甲、乙两台设备的加工,产品都必须在设备甲上加工完毕之后,才能进人设备乙上加工,各种产品在甲、乙设备上加工时间(单位:天)如表所示。