2012届华师一附中高一下学期课外综合训练题(十一)---空间几何体答案

高一课外综合训练题（九）1．△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知a ，b ，c 成等比数列，3cos 4B =． （Ⅰ）求cot cot AC +的值；（Ⅱ）设32BA BC ⋅= ,求a c +的值.解：（Ⅰ）由3cos 4B =，得sin B = 由2b ac =及正弦定理得 2sin sin sin B A C =. 11cos cos cot cot tan tan sin sin A C A C A C A C +=+=+2sin cos cos sin sin()sin sin sin C A C A A C A C B ++==2sin 1sin sin B B B === 即cot cot A C +=（Ⅱ）由32BA BC ⋅= ，得3cos 2ca B ⋅=,∵3cos 4B =，∴2ca =，22b =即.由余弦定理2222cos b a c ac B =+-，得225a c +=，222()2549a c a c ac +=++=+=，∴3a c +=．2. 已知△ABC 中，2220a a b c ---= ①，2230a b c +-+= ②，求△ABC 中最大角的度数。

解：由①知：1(1)2b c a a +=- ③，由②知：1(3)2b c a -=-+ ④，由③④联立解，1(3)(1)4b a a =-+⑤，21(3)4c a =+ ⑥，由④知b<c ，由⑤知a>3：利用⑥有22111(3)(43)(1)(3)0444c a a a a a a a -=+-=-+=-->，∴c a >，∴c 边最大，在△ABC 中C 角最大，2222221()()()()14cos 12222(3)(1)4a a a ab a bc a b c b c C ab ab a a a --++-++-====--+ ，∴120C =︒.3．在△ABC 中，角A ，B ，C 的对边分别是,,a b c ，且4cos 5A =⑴ 求2sincos 22B CA ++的值； ⑵ 若2,3ABC b S ∆==，求a . 解：（1）∵A ，B ，C 是△ABC 的内角 180222B C A A B C π+∴++=∴=-222211sin cos 2sin cos 2cos cos 2cos 2cos 1222222B C A A A A A A A π+⎛⎫∴+=-+=+=++- ⎪⎝⎭ 2211sin cos 22cos cos 222B C A A A +∴+=+-224414113cos sin cos 22.52525210B C A A +⎛⎫=∴+=⨯+⨯-= ⎪⎝⎭（2）∵A 是△ABC 的内角 43sin 0cos sin 55A A A ∴>=∴= 又又113sin 23 5.225ABC S b c A c c ∆=⋅⋅⋅=⨯⨯⨯=∴= 2222222254cos 13.22255b c a a A a bc +-+-∴===∴=⨯⨯a 是△ABC 的一边,0a a ∴>∴=4. 在ABC ∆中，角,,A B C 的对边分别为,,,3a b c B π=，4cos ,5A b == （Ⅰ）求sin C 的值； （Ⅱ）求ABC ∆的面积.解:（Ⅰ）∵A 、B 、C 为△ABC 的内角，且4,cos 35B A π==，∴23,sin 35C A A π=-=，∴21sin sin sin 32C A A A π⎛⎫=-=+=⎪⎝⎭.（Ⅱ）由（Ⅰ）知33sin ,sin 510A C +==，又∵,3B b π==在△ABC 中，sin 6sin 5b A a B ==.∴△ABC 的面积116sin 225S ab C ==⨯=. 5. 在ABC ∆中，内角A 、B 、C 的对边长分别为a 、b 、c ，已知222a c b -=，且s i n c o s 3c o s s i n ,A C A C=求b解：在ABC ∆中sin cos 3cos sin ,A C A C = 有:2222223,22a b c b c a a c ab bc+-+-=化简并整理 2222()a c b -=.又由已知222a c b -=24b b ∴=.解得40(b b ==或舍）. 解法二:由余弦定理得: 2222cos a c b bc A -=-.又222a c b -=,0b ≠。

湖北华中师范大学第一附属中学立体几何多选题试题含答案一、立体几何多选题1. 如图，正方体ABCD-ABCD中的正四而体A厂BD G的棱长为2,则下列说法正确的是（）A. 异面直线A&与所成的角是彳3B. 丄平而A^DC. 平而Acq截正四而体- BDC,所得截而而积为2D. 正四而体A - BDC｛的髙等于正方体ABCD-\B,C X D X体对角线长的;【答案】ABD【分析】选项A,利用正方体的结构特征找到异而直线所成的角；选项B,根据正方体和正四而体的结构特征以及线而垂直的判定泄理容易得证；选项C,由图得平而ACQ截正四而体 A - BDC x所得截面而积为A AC冋面积的四分之一：选项D,分别求出正方体的体对角线长和正四而体A - BDC.的高，然后判断数量关系即可得解.【详解】□ _______________ qA：正方体ABCD — AQCQ中，易处ADJIBC、,异面直线£3与所成的角即直线A"与BG所成的角，即ZA/G , LA.B G为等边三角形，ZABC,=-,正确:B：连接Bp, QB丄平面AdG®, AC|U平而AdGD，即人q丄B®又AG 丄Bp, B\BcBQ=B],有AQ 丄平而BDD 且,BQu 平而BDD X B X ,所以BD』A}C{,同理可证：BD』人》, = 所以8卩丄平而AQD ,正确:D t CiS Fic：易知平面心截正四耐本A-所得截而面积为半斗’错误;D：易得正方体ABCD- A且CQ的体对角线长为（（血丫 +（近$ +（Qf =应,棱长为2的正四而体A - BDC、的高为店-（圧正％ |卜斗故正四而体A - BDC.的髙等2于正方体ABCD-A.B^D,体对角线长的亍，正确.3故选：ABD.【点睛】关键点点睛：利用正方体的性质，找异而直线所成角的平而角求其大小，根拯线面垂直的判泄证明3。

丄平而AGD,由正四而体的性质，结合几何图形确左截而的面积，并求高，即可判断c、D的正误.2. 一副三角板由一块有一个内角为60。

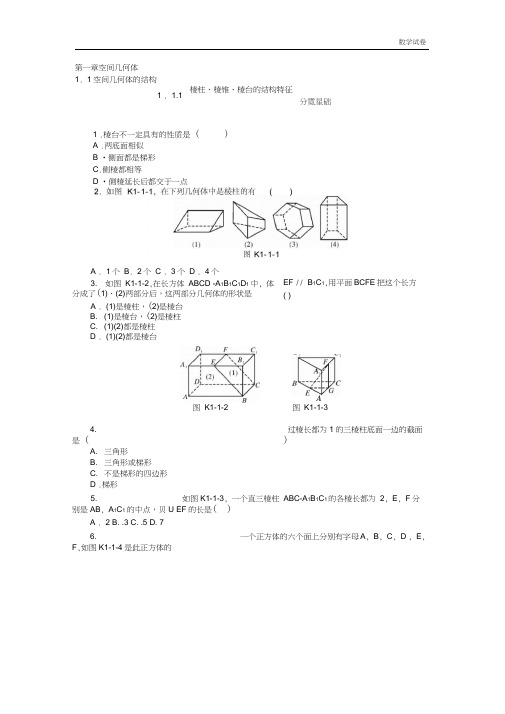
第一章空间几何体1. 1空间几何体的结构1 . 1.1棱柱、棱锥、棱台的结构特征分霓星础1 .棱台不一定具有的性质是()A .两底面相似B •侧面都是梯形C.侧棱都相等D •侧棱延长后都交于一点A . 1个B. 2个C . 3个D . 4个3. 如图K1-1-2,在长方体ABCD -A1B1C1D1 中, 体分成了(1)、(2)两部分后，这两部分几何体的形状是A . (1)是棱柱，(2)是棱台B. (1)是棱台，(2)是棱柱C. (1)(2)都是棱柱D . (1)(2)都是棱台4. 过棱长都为1的三棱柱底面一边的截面是()A. 三角形B. 三角形或梯形C. 不是梯形的四边形D .梯形5. 如图K1-1-3, 一个直三棱柱ABC-A1B1C1的各棱长都为2, E, F分别是AB, A1C1 的中点，贝U EF的长是()A . 2 B. .3 C. .5 D. 76. 一个正方体的六个面上分别有字母A, B, C, D , E, F,如图K1-1-4是此正方体的EF // B1C1,用平面BCFE把这个长方( )A图K1-1-3图K1-1-2两种不同放置，则与D面相对的面上的字母是___________ .图K1-1-4学昌申罡H7. 在四棱锥的四个侧面中，直角三角形最多可有（）A . 1个B. 2个C . 3个D . 4个& 长方体ABCD - A i B i C i D i的棱AB= 3, AD = 4, AA i= 5，则长方体的对角线长为拓展揺走9.在图Ki-i-6所示的4个平面图形中，哪几个是各侧棱都相等的四面体的展开图？其序号是 _______________ （把你认为正确的序号都填上）./w②③ ④图Ki-i-6 （如图Ki-i-5）图Ki-i-51.1.2圆柱、圆锥、圆台、球及简单组合体的结构特征分买星础1. 有下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是（）A .①②B .②③C.①③ D .②④2. 下列说法中正确的是（）A .以直角三角形的一边为轴旋转所得的旋转体是圆锥B .以直角梯形的一腰为轴旋转所得的旋转体是圆台C.圆柱、圆锥、圆台的底面都是圆D .圆锥侧面展开图为扇形，这个扇形所在圆的半径等于圆锥的底面圆的半径3. （2019年江西一模）如图K1-1-7,已知正方体ABCD -A1B1C1D1上、下底面中心分别为。

高一课外综合训练题（四）1. 已知函数)(x f 满足:3)1(),()()(=⋅=+f q f p f q p f , 求)7()8()4()5()6()3()3()4()2()1()2()1(2222f f f f f f f f f f f f +++++++的值.2. 求数列1, 3+5, 7+9+11, 13+15+17+19，…的前n 项和．3．已知数列{a n }满足a 1=1, n a =a 1+2a 2+3a 3+…+(n-1)a n-1(n ≥2), 求{n a }的通项n a .4．设2)0(1)0()],([)(,12)(111+-==+=+n n n n n f f a x f f x f xx f ，其中+∈N n ,求数列}{n a 的通项公式.5．已知：正项等比数列{a n }满足条件：① 12154321=++++a a a a a ；② 251111154321=++++a a a a a ；求{}n a 的通项公式n a6．已知函数n S x x x f ,263)(2-+-=是数列}{n a 的前n 项和，点（n ，S n ）（n ∈N*）在曲线2)(+=x f y 上，求n a .又若6,)21(1nn n n n b a c b ⋅==-，且n T 是数列{c n }的前n 项和. 求n T .7．已知,2,)0}({),0()2()(12=>≥+=a a a x x x f n n 中又数列前n 项和的公式S n （n ∈N ）对所有大于1的自然数n 都有)(1-=n n S f S ，求数列{a n }的通项公式；又若221121,.2n n n n n na ab b b b n a a +++=+++- 求8．已知数列{}n a ,S n 是它的前n 项和,且1),(2411=∈+=*+a N n a S n n 。

(1)设)(21*+∈-=N n a a b n n n ,求证:数列{}n b 是等比数列(2)设2n n na C =,,求证:数列{}n c 是等差数列。

高一课外训练题（十一）1．i , j 是两个不共线的向量,已知AB =3i +2j ,CB =i +λj ,CD =-2i +j ,若A 、B 、D 三点共线,试求实数λ的值.2．如图,M 是△ABC 内一点,且满足条件=++CM BM AM 320,延长CM 交AB 于N,令CM =a ,试用a 表示CN .3. 如图10所示,已知在△ABC 中,D 、E 、L 分别是BC 、CA 、AB 的中点,设中线AD 、BE 相交于点P .求证:AD 、BE 、CL 三线共点. ( 三角形三条中线共点 )4．已知a =AB , B(1, 0), b =(-3, 4), c =(-1, 1)，且a =3b -2c ，求点A 的坐标。

5. 若已知AC ，AB D C B A 以),3,2(),2,3(),1,2(),2,1(--为基底来表示CD BD AD ++。

6. 如图所示,已知△AOB 中,A(0,5),O(0,0),B(4,3),OC =41OA ,OD =21OB ,AD 与BC 相交于点M,求点M 的坐标.7. 已知向量u =(x, y)与向量v =(y, 2y-x)的对应关系用u =f(v)表示，（1）证明对于任意向量a , b 及常数m, n ，恒有f(m a +n b )=mf(a )+nf(b )成立；（2）设a =(1, 1), b =(1, 0)，求向量f(a )及f(b )的坐标； （3）求使f(c )=(p, q)(p, q 为常数)的向量c 的坐标。

8. 已知四边形ABCD ，E 、F 分别是AD 、BC 的中点，求证：)(21DC AB EF +=。

9．（1）设两个非零向量1e 、2e 不共线，如果12121223,623,48AB e e BC e e C D e e =+=+=-, 求证：,,A B D 三点共线.（2）设1e 、2e 是两个不共线的向量，已知1212122,3,2AB e k e C B e e C D e e =+=+=-,若,,A B D 三点共线，求k 的值.10．已知向量a =2e 1-3e 2, b =2e 1+3e 2，其中e 1、e 2不共线，向量c =2e 1-9e 2。

立体几何训练题1. 如图，在底面为平行四边形的四棱锥P ABCD -中，AB AC ⊥，PA ⊥平面ABCD ，且PA AB =，点E 是PD 的中点.（1）求证：AC PB ⊥； （2）求证：//PB 平面AEC ； （3）求二面角E AC B --的大小. 解：（1）由PA ⊥平面ABCD 可得PA ⊥AC ，又AB AC ⊥，所以AC ⊥平面PAB ，所以AC PB ⊥（2）如图，连BD 交AC 于点O ，连EO ，则EO 是△PDB 的中位线，∴EO //PB ，∴PB //平面AEC （3）如图，取AD 的中点F ，连EF ，FO ，则EF 是△PAD 的中位线，∴EF //PA 又PA ⊥平面ABCD ，∴EF ⊥平面ABCD 。

同理FO 是△ADC 的中位线，∴FO //AB ∴FO ⊥AC 由三垂线定理可知∴∠EOF 是二面角E －AC －D的平面角.又FO ＝12AB ＝12PA ＝EF ∴∠EOF ＝45︒而二面角E AC B --与二面角E －AC －D 互补，故所求二面角E AC B --的大小为135︒.2．如图，ABCD －A 1B 1C 1D 1是正四棱柱，(Ⅰ) 求证：BD ⊥平面ACC 1A 1；(Ⅱ) 若二面角C 1－BD －C 的大小为60°，求异面直线BC 1与AC 所成角的大小。

解：（I ）∵ABCD －A 1B 1C 1D 1是正四棱柱，∴ CC 1⊥平面ABCD ，∴ BD ⊥CC 1，∵ ABCD 是正方形，∴ BD ⊥AC ，又∵AC 、CC 1⊂平面ACC 1A 1，且AC∩CC 1=C ，∴ BD ⊥平面ACC 1A 1； （II ）设BD 与AC 相交于O ，连接C 1O ，∵ CC 1⊥平面ABCD ，BD ⊥AC ，，∴ BD ⊥C 1O ，∴∠C 1OC 是二面角C 1－BD －C 的平面角，∴∠C 1OC=60°，连接A 1B ，∵A 1C 1//AC ，∴∠A 1C 1B 是BC 1与AC 所成的角，设BC=a ，则CO=，CC 1=CO ·tan60°=，A 1B=BC 1=，11AC ，在△A 1BC 1中，222111111111cos 2AC BC A B AC B AC BC +-==⋅，∴∠A 1C 1B=∴ 异面直线BC 1 与AC所成的角为。

高一课外综合训练题（三）1．根据下面各数列前几项的值，写出数列的一个通项公式：（1）-1，7，-13，19，… （2）7，77，777，7777，…（3）5，0，-5，0，5，0，-5，0，… （4）1，3，6，10，15，…（5）2,(46),81012,(14161820);-+++-+++2．如图，一个粒子在第一象限运动，在第一秒内它从原点运动到(0, 1)，而后它接着按图所示在x 轴、y轴的平行方向上来回运动，且每秒移动一个单位长度，求1999秒时这个粒子所处的位置.3．定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列．这个常数叫做该数列的公和．已知数列{a n }是等和数列，且a 1=2，公和为2，求a 18的值；并求这个数列的前n 项和S n 的计算公式.4．已知)(9998*N ∈--=n n n a n ，则在数列}{n a 中的前30项中，求最大项和最小项.a．5. 求数列1，1+2+1，1+2+3+2+1，1+2+3+4+3+2+1，…的通项公式n6. 数列{a n}满足递推关系：a n=a n-2+2，且a1=1, a2=4．（1）求a3, a4；（2）求a n；（3）求数列{a n}前n项之和．7．已知{a n}是等差数列．（1）前四项和为21，末四项和为67，且各项和为286，求项数；（2）S n=20, S2n=38，求S3n；（3）若两个等差数列的前n项的和之比是(7n+1)∶(4n+27)，求它们的第11项之比．8．{a n }为等差数列，公差d ≠0,a n ≠0,(n ∈N *),且a k x 2+2a k +1x +a k +2=0(k ∈N *)(1)求证 当k 取不同自然数时，此方程有公共根； (2)若方程不同的根依次为x 1,x 2,…,x n ,…,求证 数列11,,11,1121+++n x x x 为等差数列9. 已知数列}{n a 中的),2(12,53*11N ∈≥-==-n n a a a n n ，数列}{n b 满足)(11*N n a b n n ∈-= （1）求证数列}{n b 是等差数列； （2）求数列}{n a 中的最大项与最小项；并说明理由.10. 设实数0>a ，且函数)12()1()(2a x x a x f +-+=有小值-1. （1）求a 的值；（2）设数列}{n a 的前n 项和,),(242na a ab n f S n n n +++== 令,,3,2,1 =n 证明}{n b 是等差数列.11. 设数列{a n }前n 项和为2214---=n n n a S . （1）试求1+n a 与n a 的关系； （2）试用n 表示a n 。

高一数学空间几何体试题答案及解析1.长方体的表面积是24，所有棱长的和是24，则对角线的长是（）．Ａ． B．4 C．3D．2【答案】B【解析】设出长方体的长、宽、高，表示出长方体的全面积，十二条棱长度之和，然后可得对角线的长度．【考点】长方体的结构特征，面积和棱长的关系.2.如图是一平面图形的直观图，斜边，则这个平面图形的面积是（）A．B．1C．D．【答案】D【解析】根据直观图可知,根据直观图与平面图的关系可知,平面图中, ,在轴上,且 ,所以.【考点】直观图与平面图的关系3.某工厂为了制造一个实心工件，先画出了这个工件的三视图（如图），其中正视图与侧视图为两个全等的等腰三角形，俯视图为一个圆，三视图尺寸如图所示（单位cm）；（1）求出这个工件的体积；（2）工件做好后，要给表面喷漆，已知喷漆费用是每平方厘米1元，现要制作10个这样的工件，请计算喷漆总费用（精确到整数部分）.【答案】(1) ;(2)314元【解析】(1)根据三视图可知该工件是一个圆锥的形状，其中圆的半径为2，母线长为3，所以圆锥的高 .又根据圆锥的体积公式 .可得 .故填 .(2)因为圆锥的表面积公式为.又因为，.所以.所以10个共要.所以共需要元.所以填314元.试题解析：（1）由三视图可知，几何体为圆锥，底面直径为4，母线长为3， 2分设圆锥高为，则 4分则 6分（2）圆锥的侧面积， 8分则表面积=侧面积+底面积=（平方厘米）喷漆总费用=元 11分【考点】1 三视图 2 圆锥的体积 3 圆锥的表面积4.已知一空间几何体的三视图如图所示，它的表面积是()A．B．C．D．3【答案】C【解析】该几何体是三棱柱，如下图，，其表面积为。

故选C。

【考点】柱体的表面积公式点评：由几何体的三视图来求出该几何体的表面积或者体积是一个考点，这类题目侧重考察学生的想象能力。

5.已知三棱柱，底面三角形为正三角形，侧棱底面，，为的中点，为中点．(Ⅰ)求证：直线平面；(Ⅱ）求点到平面的距离．【答案】（Ⅰ）取的中点为，连接，推出，，且，利用四边形为平行四边形，得到，所以直线平面.(Ⅱ）点到平面的距离为．【解析】（Ⅰ）取的中点为，连接，因为为的中点，为中点，所以，，且，所以四边形为平行四边形，所以，又因为,所以直线平面.(Ⅱ）由已知得，所以,因为底面三角形为正三角形，为中点，所以, 所以，由（Ⅰ）知，所以，因为，所以,,设点到平面的距离为，由等体积法得，所以，得，即点到平面的距离为．【考点】正三棱柱的几何特征，平行关系，垂直关系，体积计算，距离计算。

高一课外综合训练题（十一）1.如图所示是一个空间几何体的三视图，试用斜二测画法画出它的直观图.（尺寸不限）.2. 若棱长为3的正方体的顶点都在同一球面上求该球的表面积.3. 如图所示，表面积为324π的球，其内接正四棱柱的高是14,求这个正四棱柱的表面积.4. 如图(1)所示，E、F分别为正方体面ADD′A′、面BCC′B′的中心，则四边形BFD′E在该正方体的各个面上的投影可能是图(2)的_______________.(1) (2)5.如图，在正三棱柱ABC—A1B1C1中，AB=3，AA1=4.M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为29，设这条最短路线与CC1的交点为N，求P点的位置.6.一个底面直径为20 cm的装有一部分水的圆柱形玻璃杯，水中放着一个底面直径为6 cm，高为20 cm 的一个圆锥形铅锤，当铅锤从水中取出后，杯里的水将下降几厘米？7. 长方体AC 1的长、宽、高分别为3、2、1，求A 到C 1沿长方体的表面的最短距离8. 如图25所示，有12个小正方体，每个正方体6个面上分别写着数字1、9、9、8、4、5，用这12个小正方体拼成一个长方体，那么图中看不见的那些小正方体的面有多少个?并求这些面上的数字和.9. 一个正三棱柱容器，底面边长为a ，高为2a ，内装水若干，将容器放倒，把一个侧面作为底面，如图，这时水面恰好为中截面，求正三棱柱中容器内水面的高度.10. 有两个相同的直三棱柱，高为a 2，底面三角形的三边长分别为3a ,4a ,5a (a ＞0).用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的是一个四棱柱，求a 的取值范围.11. 如图所示的几何体是一棱长为4 cm 的正方体，若在它的各个面的中心位置上，各打一个直径为2 cm 、深为1 cm 的圆柱形的孔，求打孔后几何体的表面积是多少?（π取3.14）12. 如图18所示是由18个边长为1 cm 的小正方体拼成的几何体，求此几何体的表面积.。