四川省泸州市2021届高三上学期第一次教学质量诊断性考试数学(文)试卷

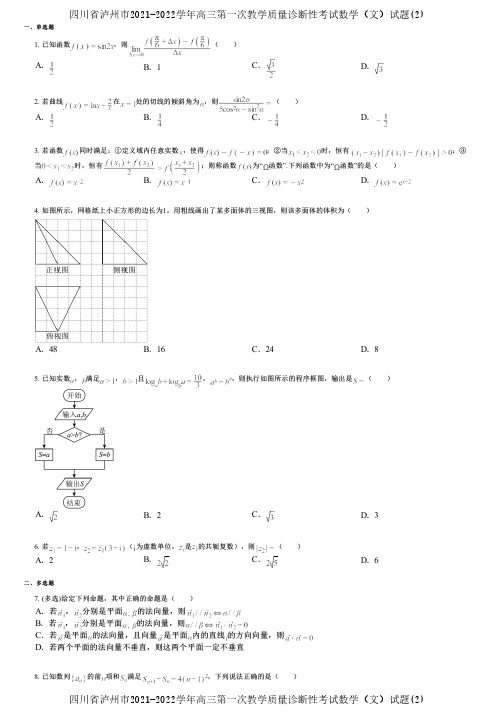
一、单选题二、多选题1. 已知函数，则（ ）A．B ．1C．D．2. 若曲线在处的切线的倾斜角为，则（ ）A．B．C．D．3. 若函数同时满足：①定义域内任意实数，使得；②当时，恒有；③当时，恒有；则称函数为“函数”.下列函数中为“函数”的是（ ）A．B．C．D．4. 如图所示，网格纸上小正方形的边长为1，用粗线画出了某多面体的三视图，则该多面体的体积为（）A ．48B ．16C ．24D ．85. 已知实数，满足，且，，则执行如图所示的程序框图，输出是（）A．B ．2C．D ．36. 若，（为虚数单位，是的共轭复数），则（ ）A ．2B．C．D ．67. (多选)给定下列命题，其中正确的命题是（ ）A ．若，分别是平面的法向量，则B ．若，分别是平面的法向量，则C．若是平面的法向量，且向量是平面内的直线的方向向量，则D ．若两个平面的法向量不垂直，则这两个平面一定不垂直8.已知数列的前项和满足，下列说法正确的是（ ）四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题(2)四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题(2)三、填空题四、解答题A ．若首项，则数列的奇数项成等差数列B ．若首项，则数列的偶数项成等差数列C ．若首项，则D ．若首项，若对任意，恒成立，则的取值范围是9. 定义为与距离最近的整数（当为两相邻整数算术平均值时，取较大整数），令函数，如：.则__________；_________.10. 为了筹办某运动会开幕式，导演组从某高校的6名男生代表和6名女生代表中选取8人加入开幕式志愿者团队．在志愿者招募的过程中，为了平衡男女比例，要求本次选取的8人中至少有3名女生，则选取的8人中男女生人数均等的概率为______．11. 已知满足对且时，（为常数），则的值为__________．12. 已知函数f(x)=f'(-1)x 2+3x-4,则f'(1)=____.13. 已知函数（）(1)当时，比较与的大小；(2)若存在两个不同的零点，，且，证明：.14. 在中，角A ，B ，C 所对的边分别为a ，b ，c ，已知．(1)证明：为等腰三角形；(2)若，，求的面积．15.记为数列的前项和，已知的等差中项为.(1)求证为等比数列；(2)数列的前项和为，是否存在整数满足？若存在求，否则说明理由.16. 已知定义在R上的奇函数满足．(1)求实数a 的值；(2)当时，用定义证明函数为单调递增函数；(3)当时，解不等式．。

一、单选题二、多选题1.已知函数，记等差数列的前n 项和为，若，，则（ ）A．B．C ．2022D ．40442. 如图，网格纸上绘制的是一个几何体的三视图，网格小正方形的边长为1，则该几何体的体积为（）A．B．C．D ．4 3. 的展开式中的系数为40，则实数a 的值为（ ）A ．4B ．2C ．1D．4. 设m ，n ，l 分别是三条不同的直线，是平面，则下列结论中正确的是（ ）A ．若，，，，则B．若，，则C ．若，，则D ．若，，则5. 下列双曲线中，焦点在y 轴上，且渐近线互相垂直的是（ ）A．B．C．D．6.在各项都为正数的等比数列中，，则（ ）A．B ．2018C．D ．20177. 设，则函数的零点位于区间A ．（2，3）B ．（1，2）C ．（0，1）D ．（-1，0）8. 设集合，，则A．B．C．D．9. 已知函数的导函数的图象经过点，记，则（ ）A ．在上单调递减B．C．的图象在内有5个对称轴D．10. P 是直线上的一个动点，过点P作圆的两条切线，A ，B 为切点，则（ ）A ．弦长的最小值为B ．存在点P，使得C ．直线经过一个定点D ．线段的中点在一个定圆上11. 已知随机变量服从正态分布，定义函数为取值不小于的概率，即，则（ ）A．B．四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题(高频考点版)四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题(高频考点版)三、填空题四、解答题C ．为减函数D．为偶函数12.已知复数，则下列各项正确的为（ ）A ．复数的虚部为B ．复数为纯虚数C ．复数的共轭复数对应点在第四象限D ．复数的模为513. 已知双曲线的右焦点为，折线与双曲线的右支交于两点（如图），则的面积为___________．14.函数的图象在点处的切线与直线平行，则的极值点是__________．15. 能够使得命题“曲线上存在四个点满足四边形是正方形”为真命题的一个实数的值为______.16. 已知数列的各项均为正数的等比数列，且，.(1)求数列的通项公式:(2)设，求数列的前项和.17.在中，内角的对边分别为，且满足.(1)求的大小；(2)若的面积为，且，求的最小值.18. 在如图所示的几何体中，底面ABCD 是边长为6的正方形，，，，，点P ，Q 分别在棱GD ，BC 上，且，，.(1)证明：平面ABCD ；(2)设H 为线段GC 上一点，且三棱锥的体积为18，求平面ACH 与平面ADH 夹角的余弦值.19. 每年的4月23日是世界读书日，设立的目的是推动更多的人去阅读和写作，享受阅读带来的乐趣某高校为了解在校学生的每周阅读时间（单位：小时），对全校学生进行了问卷调查从中随机抽取了名学生的数据，统计如下表：每周阅读时间频率（1）根据频率分布表，估计这名学生每周阅读时间的平均值（同一组数据用该组数据区间的中点值表示）；（2）若认为目前该校学生每周的阅读时间服从正态分布，用（1）中的平均值近似代替，且，若某学生周阅读时间不低于小时，该同学可获得“阅读之星”称号.学校制定如下奖励方案：“阅读之星”可以获赠次随机购书卡，其他同学可以获赠次随机购书卡.每次获赠的随机购书卡的金额和对应的概率为：购书卡的金额（单位：元）概率记（单位：元）为甲同学参加问卷调查获赠的购书卡的金额，求的分布列与数学期望.20. 在中，内角，，所对的边分别为，，，且．(1)求；(2)若，求．21. 设是数列的前项和，，，.(1)求的通项；(2)设，求数列的前项和.。

2021届四川省泸州市高三第一次教学质量诊断性考试数学（文）试题一、单选题1．已知集合{0,1,2,3}A =，集合{|2}B xx =≤‖，则A B =（ ）A ．{3}B ．{0,1,2}C ．{1,2}D ．{0,1,2,3}【答案】B【解析】可以求出集合B ，然后进行交集的运算即可． 【详解】 解：{0,1,2,3},{|22}A B x x ==-≤≤，{0,1,2}A B ∴⋂=．故选：B ． 【点睛】本题考查集合交集的运算，属于基础题．2．下列函数()f x 中，满足“对任意12,(0,)x x ∈+∞，且12x x <都有()()12f x f x >”的是（ ）A ．()f x =B ．()2xf x -=C ．()ln f x x =D ．3()f x x =【答案】B【解析】对任意12,(0,)x x ∈+∞，且12x x <都有()()12f x f x >”，可知函数()f x 在(0,)+∞上单调递减，结合选项即可判断． 【详解】解：“对任意12,(0,)x x ∈+∞，且12x x <都有()()12f x f x >”， ∴函数()f x 在(0,)+∞上单调递减，结合选项可知，()f x =(0,)+∞单调递增，不符合题意，1()22xxf x -⎛⎫== ⎪⎝⎭在(0,)+∞单调递减，符合题意， ()ln f x x =在(0,)+∞单调递增，不符合题意，3()f x x =在(0,)+∞单调递增，不符合题意，故选：B ． 【点睛】本题主要考查了基本初等函数的单调性的判断，属于基础试题． 3．“sin 0α=”是“sin 20α=”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 【解析】由sin 0α=可得α，由sin 20α=也可得α，观察两个α的范围之间的关系即可得结果.【详解】 解：由sin 0α=可得,k k Z απ=∈，由sin 20α=可得,2kk Z απ=∈， 所以“sin 0α=”是“sin 20α=”的充分不必要条件，故选：A. 【点睛】本题考查条件的充分性和必要性，关键是求出α的取值，本题是基础题. 4．已知函数y =f （x ）+x 是偶函数，且f （2）=1，则f （-2）=（ ） A ．2 B ．3C ．4D ．5【答案】D【解析】∵()y f x x =+是偶函数 ∴()()f x x f x x +=--当2x =时，()()2222f f +=--，又()21f = ∴()25f -= 故选：D5．一条直线若同时平行于两个相交平面，则这条直线与这两个平面的交线的位置关系是( ) A ．异面 B ．平行 C ．相交 D ．不确定 【答案】B【解析】如图所示，直线a ∥α，a ∥β，α∩β=b ，求证a ∥b ．只需考虑线面平行的性质定理及平行公理即可．解：由a ∥α得，经过a 的平面与α相交于直线c ，则a ∥c ，同理，设经过a 的平面与β相交于直线d ， 则a ∥d ，由平行公理得：c ∥d ，则c ∥β，又c ⊂α，α∩β=b ，所以c ∥b ， 又a ∥c ，所以a ∥b ． 故答案为B ．6．函数()()1ln f x x x =-的图象可能为（ ）A ．B ．C ．D ．【答案】A【解析】根据函数定义域以及函数值正负识别函数图象，并进行选择. 【详解】当1x >时()()()1ln 1ln 0f x x x x x =-=->，所以舍去B,C; 当0x =时()()1ln f x x x =-无意义，所以舍去D; 故选：A 【点睛】本题考查函数图象的识别，考查基本分析判断能力，属基础题.7．已知:0,2p πα⎛⎫∀∈ ⎪⎝⎭，sin αα<，0:q x ∃∈N ，200210x x --=，则下列选项中是假命题的为（ ）A ．p q ∨B ．()p q ∧-C ．p q ∧D ．()p q ∨-【答案】C【解析】命题p ：由三角函数定义，即可判断出真假；命题q ：由求根公式，即可判断出真假，根据复合命题真值表判断结果即可． 【详解】解：命题p ：由三角函数的定义，角α终边与单位圆交于点P ， 过P 作PM x ⊥轴，垂足是M ，单位圆交x 轴于点A ，则sin MP α=，弧长PA 即为角α；显然MP <弧长PA ； ∴:0,2p πα⎛⎫∀∈ ⎪⎝⎭，sin αα<是真命题； 命题q ：解方程200210x x --=，则12x = 因此0:q x ∃∈N ，200210x x --=，是假命题．则下列选项中是假命题的为p q ∧．而A ，B ，D 都是真命题． 故选：C ． 【点睛】本题考查了三角函数的定义，方程的求根公式、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．8．函数()()sin 22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象向左平移6π个单位后关于y 轴对称，则函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最小值为（ ） A ．3B ．12-C ．12D ．32【解析】利用平移后的图像关于y 轴对称求出ϕ，再利用三角函数的性质可求其在给定范围上的最小值. 【详解】平移得到的图像对应的解析式为()sin 23g x x πϕ⎛⎫=++⎪⎝⎭， 因为()g x 为偶函数，所以()0sin 13g πϕ⎛⎫=+=± ⎪⎝⎭，所以32k ππϕπ+=+，其中k Z ∈.因为2πϕ<，所以6π=ϕ， 当0,2x π⎡⎤∈⎢⎥⎣⎦时，72666x πππ≤+≤，所以1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭， 当且仅当2x π=时，()min 12f x =-，故选B. 【点睛】本题考查三角函数的图像变换及正弦型函数的最值的求法，属于中档题.9．我国古代数学名著《九章算术》中，割圆术有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程，+中，“…”即代表无限次重复，但原式却是个定值x ，x =确定x 的值，的值为（ ）A ．3B ．12C ．6D ．【答案】A【解析】通过已知得到求值方法：先换元，再列方程，解方程，求解（舍去负根），再运用该方法，注意两边平方，得到方程，解出方程舍去负的即可． 【详解】(0)m m =>，则两边平方得，则23m +=， 即232m m +=，解得，3,1m m ==-舍去．【点睛】本题考查类比推理的思想方法，考查从方法上类比，是一道中档题．10．若将甲桶中的a L 水缓慢注入空桶乙中，则x min 后甲桶中剩余的水量符合衰减函数()nxf x ae =（其中e 是自然对数的底数）.假设过5 min 后甲桶和乙桶的水量相等，再过m min 后，甲桶中的水只有L 4a ，则m 的值为（ ） A ．9 B ．7 C ．5 D ．3【答案】C【解析】由题意，函数()nxy f x ae ==满足1(5)2f a =，解出11ln 52n =．再根据1()4f k a =，建立关于k 的指数方程，由对数恒成立化简整理，即可解出k 的值，由5m k =-即可得到． 【详解】解：∵5min 后甲桶和乙桶的水量相等，∴函数()nty f t ae ==，满足51(5)2nf aea ==可得11ln 52n =， 因此，当k min 后甲桶中的水只有4a升， 即1()4f k a =， 即111ln k ln 524⋅=， 即为111ln 2ln 522k ⋅=，解之得10k =，经过了55k -=分钟，即5m =． 故选：C ． 【点睛】本题给出实际应用问题，求经过几分钟后桶内的水量剩余四分之一．着重考查了指数函数的性质、指数恒等式化简，指数方程和对数的运算性质等知识，属于中档题．11．在四棱锥P ABCD -中，PA ABC ⊥平面，且ABC ∆为等边三角形，3AB =，2PA =，则三棱锥P ABC -的外接球的表面积为（ ）A ．4πB ．16πC ．8πD ．32π【答案】B【解析】先确定三棱锥P ABC -的外接球球心位置，再列方程求解球半径，最后根据球表面积公式得结果. 【详解】由题意得三棱锥P ABC -的外接球球心在过ABC ∆中心1O 且垂直平面ABC 的直线上，设为点O ，球半径设为R ,则111,31322PAOO AO R ====+=,从而外接球的表面积为2416R ππ=, 故选：B 【点睛】本题考查锥体外接球及其表面积，考查空间想象能力以及基本分析求解能力，属中档题.12．已知函数3()log f x x =的图象与函数()g x 的图象关于直线y x =对称，函数()h x 是最小正周期为2的偶函数，且当[0,1]x ∈时，()()1h x g x =-，若函数()()y k f x h x =⋅+有3个零点，则实数k 的取值范围是（ ） A ．()71,2log 3 B ．()52,2log 3-- C ．()52log 3,1--D ．71log 3,2⎛⎫-- ⎪⎝⎭【答案】B【解析】把函数()()y k f x h x =⋅+有3个零点，转化为3log ()k x h x =-有3个不同根，画出函数3log y k x =与()y h x =-的图象，转化为关于k 的不等式组求解．【详解】解：由函数3()log f x x =的图象与函数()g x 的图象关于直线y x =对称，得()3xg x =，函数()h x 是最小正周期为2的偶函数，当[0,1]x ∈时，()()131xh x g x =-=-， 函数()()y k f x h x =⋅+有3个零点，即3log ()k x h x =-有3个不同根，画出函数3log y k x =与()y h x =-的图象如图：要使函数3log y k x =与()y h x =-的图象有3个交点，则k 0<，且33log 32log 52k k >-⎧⎨<-⎩，即522log 3k -<<-． ∴实数k 的取值范围是()52,2log 3--． 故选：B ． 【点睛】本题考查函数零点与方程根的关系，考查数形结合的解题思想方法与数学转化思想方法，是中档题．二、填空题13．函数()2log f x x =-的定义域为_________． 【答案】(]0,1【解析】根据偶次根式被开方数非负列不等式，解对数不等式得结果. 【详解】由题意得22log 0log 001x x x -≥∴≤∴<≤ 故答案为：(]0,1 【点睛】本题考查函数定义域以及对数不等式，考查基本分析求解能力，属基础题.14．设函数2,05()(5),5x x f x f x x ⎧≤<=⎨-≥⎩，那么(18)f 的值为________.【答案】9【解析】推导出(18)(353)(3)f f f =⨯+=，由此能求出结果．【详解】解：∵函数2,05()(5),5x x f x f x x ⎧≤<=⎨-≥⎩，∴2(18)(353)(3)39f f f =⨯+===． 故答案为：9． 【点睛】本题考查函数值的求法，考查函数性质等基础知识，考查运算求解能力，是基础题． 15．函数()cos22sin x x f x =+的最小值为______. 【答案】3-【解析】先根据二倍角余弦公式将函数转化为二次函数，再根据二次函数性质求最值. 【详解】()2cos22sin 12sin 2sin x x x f x x =+=-+所以令sin t x =，则()22132212(),[1,1]22y t t t t f x ==-++=--+∈- 因此当1t =-时，()f x 取最小值3-， 故答案为：3- 【点睛】本题考查二倍角余弦公式以及二次函数最值，考查基本分析求解能力，属基础题.16．已知正方体有8个不同顶点，现任意选择其中4个不同顶点，然后将它们两两相连，可组成平面图形成空间几何体.在组成的空间几何体中，可以是下列空间几何体中的________.（写出所有正确结论的编号） ①每个面都是直角三角形的四面体； ②每个面都是等边三角形的四面体； ③每个面都是全等的直角三角形的四面体；④有三个面为等腰直角三角形，有一个面为等边三角形的四面体. 【答案】①②④【解析】画出正方体的图形，在几何体中找出满足结论的图形即可． 【详解】 解：①每个面都是直角三角形的四面体；如：E −ABC ，所以①正确； ②每个面都是等边三角形的四面体；如E −BGD ，所以②正确； ③每个面都是全等的直角三角形的四面体：这是不可能的，③错误；④有三个面为等腰直角三角形，有一个面为等边三角形的四面体．如：A −BDE ，所以④正确； 故答案为：①②④． 【点睛】本题考查命题的真假的判断，空间几何体的与三棱锥的关系，是基本知识的考查，易错题．三、解答题 17．已知函数321()3f x x x ax =-+（其中a 为实数）. （1）若1x =-是()f x 的极值点，求函数()f x 的减区间； （2）若()f x 在(2,)-+∞上是增函数，求a 的取值范围. 【答案】（1）(1,3)- （2）[1,)+∞【解析】（1）对()f x 求导，代入1x =-使导函数为零，求出a 的值，进而利用导数可求出()f x 的减区间.（2）()f x 在(2,)-+∞上是增函数转化为'()f x 在(2,)-+∞上大于等于零恒成立，进而转化为最值问题，即可求得a 的取值范围. 【详解】解：（1）因为321()3f x x x ax =-+，所以2()2f x x x a '=-+， 因1x =-是()f x 的极值点，所以(1)0f '-=，即120a ++=，所以3a =-， 故2()23f x x x '=--，当1x <-或3x >时，()0f x '>，当13x时，()0f x '<，所以3a =-符合题意， 且()f x 的减区间为(1,3)-；（2）因为()f x 在(2,)-+∞上为增函数，所以2()20f x x x a '=-+≥在(2,)-+∞上恒成立， 所以22a x x ≥-+在(2,)-+∞上恒成立，因为2()2g x x x =-+在(2,1)-上是增函数，在(1,)+∞上是减函数， 所以()(1)1g x g ≤=，所以1a ≥，即a 的取值范围为[1,)+∞， 【点睛】本题考查函数的极值及单调性，其中关键是将单调性问题转化为最值问题，是中档题. 18．在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，已知()cos sin c a B B =-. （Ⅰ）求A ；（Ⅱ）已知c =，BC 边上的高1AD =，求b 的值.【答案】（Ⅰ）34A π=（Ⅱ）b =【解析】（Ⅰ）先根据正弦定理将边角关系化为角的关系，再根据两角和正弦公式化简求结果，（Ⅱ）先根据三角形面积公式得到a =，再利用余弦定理求b 的值. 【详解】解：（Ⅰ）由()cos sin c a B B =-， 及正弦定理得()sin sin cos sin C A B B =-， 即()sin sin cos sin sin A B A B A B π-+=-⎡⎤⎣⎦， 所以sin cos cos sin sin cos sin sin A B A B A B A B +=-， 即cos sin sin sin 0A B A B +=，由于B 为ABC ∆的内角，所以sin 0B ≠， 所以tan 1A =-， 又()0,A π∈，所以34A π=； （Ⅱ）因为11sin 22S bc A AD a ==⋅，代入c =1AD =，sin A =a =，由余弦定理得22222cos 10a b c bc A b =+-=++，代入a =，得24100b --=，解得b =b =，所以b =【点睛】本题考查正弦定理、余弦定理以及三角形面积公式，考查基本分析求解能力，属中档题. 19．已知函数()()2cos sin cos 1f x x x x =+-()x R ∈. （Ⅰ）求函数()f x 的最小值及取最小值时x 取值的集合；（Ⅱ）若将函数()f x 的图象上所有点的横坐标扩大为原来的4倍，纵坐标不变，得到函数()g x 的图象，且()15g a =，3,22a ππ⎛⎫∈ ⎪⎝⎭，求2g a π⎛⎫- ⎪⎝⎭的值.【答案】（Ⅰ）最小值是x 的集合为3|,8x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭；（Ⅱ）5【解析】（Ⅰ）先根据二倍角正余弦公式以及辅助角公式化简函数，再根据正弦函数性质求最值， （Ⅱ）先根据三角函数图象变换得()g x 解析式，再根据两角差正弦公式求结果. 【详解】解：（Ⅰ）()22cos sin 2cos 1f x x x x =+-，sin 2cos2x x =+24x π⎛⎫=+ ⎪⎝⎭，当2242x k πππ+=-+，即38x k ππ=-()k Z ∈时，sin 24x π⎛⎫+ ⎪⎝⎭取得最小值是1-，所以函数()f x 的最小值是， 此时x 的集合为3|,8x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭； （Ⅱ）()f x 的图像上所有点的横坐标扩大为原来的4倍，纵坐标不变，得到函数()g x ，所以()g x 的最小正周期为4π，故()124g x x π⎛⎫=+ ⎪⎝⎭因为()11245g a a π⎛⎫=+= ⎪⎝⎭，所以1sin 2410a π⎛⎫+=⎪⎝⎭. 又3,22a ππ⎛⎫∈⎪⎝⎭，所以1,242a πππ⎛⎫+∈ ⎪⎝⎭，所以1cos 2410a π⎛⎫+=-⎪⎝⎭， 1122244g a a a πππ⎡⎤⎛⎫⎛⎫-==+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦11sin cos cos sin 244244a a ππππ⎤⎛⎫⎛⎫=+-+ ⎪ ⎪⎥⎝⎭⎝⎭⎦102102⎛=--⨯ ⎥⎝⎭⎣⎦5=. 【点睛】本题考查两角差正弦公式、二倍角正余弦公式、辅助角公式、三角函数图象变换以及正弦函数性质，考查综合分析求解能力，属中档题.20．如图，已知BD 为圆锥AO 底面的直径，点C 是圆锥底面的圆周上，2AB BD ==，6BDC π∠=，AE ED =，F 是AC 上一点，且平面BFE ⊥平面ABD .（Ⅰ）求证AD BF ⊥； （Ⅱ）求多面体BCDEF 的体积. 【答案】（Ⅰ）证明见解析 （Ⅱ）310【解析】（Ⅰ）先根据等腰三角形性质得AD BE ⊥，再根据面面垂直性质定理得AD BEF ⊥平面，即可证得结果，（Ⅱ）先求A BEF V -，根据等体积法或求高可得A BEF V -，再根据A BEF V -与多面体BCDEF 的体积关系得结果. 【详解】解：（Ⅰ）因为ABD ∆是等边三角形，AE ED =， 所以AD BE ⊥，因为平面BFE ABD ⊥平面，且交线为BE ， 所以AD BEF ⊥平面， 因为BF BEF ⊂平面，所以AD BF ⊥；（Ⅱ）解法一：因为30BDC ∠=︒，90BCD ∠=︒，2BD =，所以3CD =4435cos 2228CAD +-∠==⨯⨯，在Rt AEF ∆中，5cos 8AE CAD AF ∠==，又1AE =， 所以85AF =，25CF =，所以点F 到平面ABE 的距离为点C 到平面ABE 的距离的45， 所以三棱锥F ABE -的体积142255F ABE C ABD A BCD V V V ---=⨯=， 所以多面体BCDEF 的体积为35BCDEFA BCD V V -=3153BCD S AO ∆=⨯⋅135210=⨯=.解法二：5EF =，BE =在ABC ∆中，7cos 8BAC ∠=，BF =，在BEF ∆中，cos BFE ∠=，所以sin BFE ∠=从而1325BEF S ∆==， 由（Ⅰ）可知AD BEF ⊥平面，所以113113355A BEF BEF V S -∆=⨯⨯=⨯=， 又因为1132A BCD BCD V S AO -∆=⨯⨯=，所以多面体BCDEF 的体积为1132510BCDEF A BCD A BEF V V V --=-=-=. 【点睛】本题考查面面垂直性质定理、线面垂直性质定理以及锥体体积公式，考查综合分析求解能力，属中档题. 21．已知函数()ln f x x =，()1g x a x=+（其中a 是常数）. （Ⅰ）求过点()0,1P -与曲线()f x 相切的直线方程； （Ⅱ）是否存在1k ≠的实数，使得只有唯一的正数a ，当1x a >时不等式()1f x g x kx a ⎛⎫-≤ ⎪⎝⎭恒成立，若这样的实数k 存在，试求k ，a 的值；若不存在，请说明理由．【答案】（Ⅰ）1y x =-（Ⅱ）存在实数2k e =，a 【解析】（Ⅰ）先求导数，根据导数几何意义用切点坐标表示切线斜率，再根据点斜式得切线方程，最后根据切线过点求切点坐标，即得结果,（Ⅱ）先化简不等式，构造函数()21ln k k m x x x x a a a ⎛⎫=-+> ⎪⎝⎭，利用导数研究新函数单调性，确定最小值取法，再根据最小值不大于零，结合解得唯一性确定k ，a 的值. 【详解】解：（Ⅰ）设过点()0,1P -的直线与曲线()f x 相切于点()00,ln x x ， 因()ln f x x =，则()1f x x'=， 所以在()00,ln x x 处切线斜率为()001f x x '=， 则在()00,ln x x 处切线方程为()0001ln y x x x x -=-， 将()0,1P -代入切线方程，得0ln 0x =， 所以01x =，所以切线方程为1y x =-；（Ⅱ）假设存在1k ≠的正实数，使得只有唯一的正数a ，当1x a >时不等式()1f x g x kx a ⎛⎫-≤ ⎪⎝⎭恒成立，即2ln 1a xx kx ax ≤-恒成立， 因为1x a >，所以()21ln k ax x a -≤，即()21ln 0k ax x a--≤， 令()()2211ln ln k ax k k m x x x x x a a a a -⎛⎫=-=-+> ⎪⎝⎭则()1k m x x a '=-，由于()00m x '=，即0a x k =， （1°）当1a k a>即20k a <<时，01,x x a ⎛⎫∈ ⎪⎝⎭时，()00m x '>，则()m x 在01,x a ⎛⎫ ⎪⎝⎭上为增函数，()0,x x ∈+∞时，()00m x '<，则()m x 在()0,x +∞上为减函数，则()()02min 1ln 0k a m x m x a k==-++≤， 即2ln 1k a a k +≤，令()(2lnk ah a a a k=+>， 则()233122k a k h a a a a-'=-=，由()00h a '=，得0a a =>，)0a a ∈时，()0h a '<，则()h a在区间)0a 上为减函数，()0,a a ∈+∞时，()0h a '>，则()h a 在区间()0,a +∞上为增函数，因此存在唯一的正数a >()1h a ≤，故只能()min 1h a =.所以()()0min 1ln 12h a h a ==+=， 所以2k e =，此时a只有唯一值e. （2°）当1a k a ≤即2k a ≥时，()0m x '>，所以()m x 在1,a ⎛⎫+∞ ⎪⎝⎭上为增函数， 所以()11lim ln0x am x a→=≤，即1a ≥，故1k >.所以满足1a ≤≤a 不唯一，综上，存在实数2k e =，a，当1x a >时，恒有原式成立. 【点睛】本题考查导数几何意义以及利用导数研究不等式恒成立问题，考查综合分析求解能力，属难题. 22．如图，在极坐标系Ox 中，过极点的直线l 与以点(2,0)A 为圆心、半径为2的圆的一个交点为2,3B π⎛⎫⎪⎝⎭，曲线1M 是劣弧OB ，曲线2M 是优弧OB .（1）求曲线1M 的极坐标方程；（2）设点()1,P ρθ为曲线1M 上任意一点，点2,3Q πρθ⎛⎫- ⎪⎝⎭在曲线2M 上，若||||6OP OQ +=，求θ的值.【答案】（1）4cos 32ππρθθ⎛⎫=≤≤ ⎪⎝⎭（2）3πθ=【解析】（1）利用参数方程极坐标方程和直角坐标方程之间的转换，求出结果． （2）利用极径和三角函数关系式的变换的应用求出结果． 【详解】解：（1）设以点(2,0)A 为圆心、半径为2的圆上任意一点(,)ρθ， 所以该圆的极坐标方程为4cos ρθ=， 则1M 的方程为4cos 32ππρθθ⎛⎫=≤≤⎪⎝⎭；（2）由点()1,P ρθ为曲线1M 上任意一点，则114cos 32ππρθθ⎛⎫=≤≤⎪⎝⎭，点2,3Q πρθ⎛⎫- ⎪⎝⎭在曲线2M 上，则24cos 3233ππππρθθ⎛⎫⎛⎫=--≤-≤ ⎪⎪⎝⎭⎝⎭， 即224cos 363πππρθθ⎛⎫⎛⎫=--≤≤ ⎪⎪⎝⎭⎝⎭， 因为12||,||OP OQ ρρ==，所以12||||OP OQ ρρ+=+，即||||4cos 4cos 3OP OQ πθθ⎛⎫+=+- ⎪⎝⎭3πθ⎛⎫=+ ⎪⎝⎭，因为32ππθ≤≤，且263ππθ-≤≤，所以32ππθ≤≤，因为||||6OP OQ +=，所以63πθ⎛⎫+= ⎪⎝⎭，即sin 32πθ⎛⎫+= ⎪⎝⎭， 所以3πθ=.【点睛】本题考查参数方程极坐标方程和直角坐标方程之间的转换，极径的应用，三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算能力和转换能力，属于基础题． 23．设()|-3||4|f x x x =+-. （1）解不等式()2f x ≤；（2）已知x ，y 实数满足2223(0)x y a a +=>，且x y +的最大值为1，求a 的值.【答案】（1）[2.5,4.5] （2）65a =【解析】（1）讨论x 的取值范围，去掉绝对值求出不等式()2f x ≤的解集； （2）结合题意，利用柯西不等式求得2()x y +的最大值，列方程求出a 的值．【详解】解：（1）当3x <时，不等式化为342x x -+-+≤，此时2.53x ≤<， 当34x ≤≤时，不等式化为342x x --+≤，成立， 当4x >时，不等式化为342x x -+-≤，此时4 4.5x <≤， 综上所述，原不等式的解集为[2.5,4.5]；（2）柯西不等式得22222))()x y ⎡⎤⎡⎤++≥+⎢⎥⎣⎦⎢⎥⎣⎦，因为2223(0)x y a a +=>， 所以25()6x y a +≤，（当23x y =时，取等号），又因为x y +的最大值为1，所以65a =. 【点睛】本题考查了含有绝对值的不等式解法与应用问题，也考查了柯西不等式的应用问题，是中档题．。

学习界的x + 3 - 39 -(-x)2(-x)2 -9 9 -x2x2 - 9⎩专题04 函数的奇偶性的判断及其应用【高考地位】函数的奇偶性是函数的一个重要性质，几乎是每年必考的内容，例如判断和证明函数的奇偶性，利用函数的奇偶性解决实际问题．类型一函数奇偶性的判断例1 判断下列函数的奇偶性：(1) f (x) (2) f (x) = (x +(3) f (x) =.【解析】（1）第一步，确定函数的定义域：⎧⎪9-x2≥0{}由不等式⎨⎪x2-9≥0得x =±3 ，所以函数的定义域为-3，3第二步，判断其定义域是否关于原点对称：因为函数的定义域为{-3，3}，所以定义域关于原点对称第三步，若是，则确定f (x) 与f (-x) 的关系；若不是，则既不是奇函数也不是偶函数；f (-x)=+=+=f (x)4 - x 2⎩ 第四步，得出结论. 所以函数为偶函数。

（2） 第一步，确定函数的定义域：由不等式1- x ≥ 0 得-1 < x ≤ 1 ，所以函数的定义域为(-1，1]1+ x第二步，判断其定义域是否关于原点对称：因为函数的定义域为(-1，1]，所以定义域不关于原点对称第三步，得出结论.所以函数既不是奇函数也不是偶函数；。

（3） 第一步，确定函数的定义域：⎧⎪4 - x 2≥ 0[ ) ( ] 由不等式 ⎨⎪ x + 3 - 3 ≠ 0得- 2 ≤ x < 0 或0 < x ≤ 2 ，所以函数的定义域为 - 2，0 ⋃ 或 0，2第二步，判断其定义域是否关于原点对称：因为函数的定义域为[- 2，0)⋃ 或(0，2]，所以定义域关于原点对称第三步，若是，则确定 f (x ) 与 f (-x ) 的关系；若不是，则既不是奇函数也不是偶函数；f (- x ) = - x= - x = - f (x )第四步，得出结论. 所以函数为寄函数。

【点评】确定函数的奇偶性时，必须先判定函数定义域是否关于原点对称．若对称，再验证 f (-x ) = ± f (x )或其等价形式 f (-x ) ± f (x ) = 0 是否成立．4 - (- x )2【变式演练1】【四川省泸州市2021 届高三第一次教学质量诊断性考试数学（文科）】下列函数中，在定义域上单调递增且为奇函数的是（）A. f (x) =1xB. f ( x) = sin xC. f (x) =x cos x D．f (x) =x + sin x【答案】D【分析】利用初等函数的奇偶性逐一分析选项，利用导数判断含有三角函数的单调性即可.【详解】解：A 选项：f (x) =1为奇函数，在(-∞, 0)和(0, +∞)上单调递减，故A 错误；xB 选项：f ( x) = sin x 定义域为(-∞, +∞)，但在定义域上不单调，故B 错误；C 选项：f (x) =x cos x ，定义域为(-∞, +∞)且为奇函数，取x ∈⎛0,π⎫，f (x)> 0 ，取x ∈⎛π,π⎫，1 2 ⎪ 1 2 2 ⎪⎝⎭⎝⎭ f(x2)<0，x1<x2，f(x1)>f(x2)，在(0,+∞)上不是单调增函数，故C错误；D 选项：f (x) =x + sin x ，定义域为(-∞, +∞)且为奇函数，f '( x) = 1 + cos x ≥ 0 ，故f (x) 在(-∞, +∞)上单调递增，故D 正确.故选：D.【点睛】本题考查判断已知函数的奇偶性和单调性，属于中档题.结论点睛：（1）奇函数加奇函数为奇函数；（2）偶函数加偶函数为偶函数；（3）奇函数乘奇函数为偶函数；（4）偶函数乘偶函数为偶函数；（5）奇函数乘偶函数为奇函数.【变式演练2】【四川省宜宾市2021 届高三上学期第一次诊断考试数学（文）】函数f (x) =-sin x +x cos x 部分图象大致形状为（）A．B．C．D．【答案】C【分析】利用奇偶性的定义可证f (x) 是奇函数，在利用导函数研究单调性即可确定函数图象.【详解】由解析式知：f (-x) =-sin(-x) + (-x) cos(-x) = sin x -x cos x =-f (x) ，即f (x) 是奇函数，且f (0) = 0 ，即可排除A、B；因为f '( x) =-x sin x ，所以0 <x <π时f '(x) < 0 有f (x) 单调递减，排除D；2故选：C【变式演练3】已知函数f x = log a x + 1 ，g x = log a1 − x （其中a > 0，且a ≠ 1）.a a a（1） 求函数 f x + g x 的定义域.（2） 判断函数 f x − g x 的奇偶性，并予以证明.（3） 求使 f x + g x < 0 成立的 x 的集合.【答案】（1） x| − 1 < x < 1,x ∈ R ；（2）见解析；（3）{x|0<x<1 或− 1 < x < 0【解析】（I ）由题意得： {x + 1 > 0，1 − x > 0∴− 1 < x < 1，∴所求定义域为 x| − 1 < x < 1,x ∈ R ．（II ） 函数 f x − g x 为奇函数，令 H x = f x − g x ，则 H x = log x + 1 − log 1 − x = log x+1， 1−x∵H − x = log a −x+1 =− log a x+1 =− H x ．1+x1−x∴函数 H x = f x − g x 为奇函数．（III ）∵f x + g x = log a x + 1 + log a 1 − x = log a 1 − x 2 < 0 = log a 1，∴当 a > 1 时， 0 < 1 − x 2 < 1，∴0 < x < 1 或 − 1 < x < 0．当 0 < a < 1 时， 1 − x 2 > 1，不等式无解，综上：当 a > 1 时，使 f x + g x < 0 成立的 x 的集合为{x|0<x<1 或− 1 < x < 0 ．【点睛】本题主要考查对数函数的图象和性质的综合应用，考查函数的奇偶性和单调性的运用，属于中档题．类型二 利用函数的奇偶性求函数的解析式⎨( )x 1- x, 解题模板 第一步 首先设出所求区间的自变量 x ；第二步 运用已知条件将其转化为已知区间满足的 x 的取值范围； 第三步 利用已知解析式确定所求区间相应的函数的表达式.例 2 ．已知函数 f ( x ) 是定义在 R 上的奇函数，当 x ≥ 0 时， f (x ) =x (1 + x ) ，求出函数 f ( x ) 的解析式.【答案】{x (1+ x ), x ≥ 0x (1- x ), x < 0 .【解析】第一步，首先设出所求区间的自变量 x ： 设 x < 0 则- x > 0 ，第二步，运用已知条件将其转化为已知区间满足的 x 的取值范围： 所以 f (- x ) = -x (1- x )，又因为函数 f ( x ) 是定义在 R 上的奇函数，所以- f (x ) = f (- x ) = -x (1- x )，即 f (x ) = x (1- x )，第三步，利用已知解析式确定所求区间相应的函数的表达式：所以函数的解析式为 f (x ) = ⎧x (1+ x )，x ≥ 0⎩【点评】（1）已 知函数的奇偶性求解析式的题目，一般是求哪个区间，则设未知数在哪个区间，然后化为已知区间求解；（2）本题是求函数 f ( x ) 在 R 上的解析式，一定不要忘记 x = 0时，函数 f ( x ) 的值.例 3 若函数 f ( x ) 是奇函数，g ( x ) 是偶函数，且其定义域均为{x x ∈ R , x ≠ ±1} .若 f ( x ) + g (x ) = 求 f ( x ) ， g ( x ) 的解析式.1，x -1【答案】 f (x ) =xx 2-1， g ( x ) = 1x 2 -1 .⎪ 【解析】第一步，首先设出所求区间的自变量 x ：用- x 代换解析式中的 x ，所以 f (- x )+ g (- x ) =1，- x -1第二步，运用已知条件将其转化为已知区间满足的 x 的取值范围：因为函数 f ( x ) 是奇函数， g ( x ) 是偶函数，所以 f (- x )+ g (- x ) = f (x )- g (x ) =1，- x -1第三步，利用已知解析式确定所求区间相应的函数的表达式：⎧ f (x )- g (x ) = 联立1 - x -1 ，解之得 f (x ) = x ， g ( x ) = 1 . ⎨ ⎪ f (x )+ g (x ) =⎩1 x -1 x 2-1 x 2 -1【点评】这里运用了构造法，把符合要求的奇函数与偶函数构造出来，问题也就解决了，构造的关键是运用奇、偶函数的概念，并联系方程组的知识.【变式演练 4】已知函数 f x 是定义在 R 上的奇函数,当 x > 0 时, f x = log 2 x + 1（1） 求函数 f x 的解析式;（2） 若 f m <− 2,求实数 m 的取值范围.【答案】（1）f x = log 2 x + 1 ,x〉0 0,x = 0 − log 2 1 − x ,x〈0（2）m <− 3【解析】（1）∵x > 0 时, f x = log 2 x + 1 ),∴当 x < 0 时，− x > 0,∴f − x = log 2 − x + 1 ),∵函数 f x 是定义在 R 上的奇函数,∴f − x =− f x ∴− f x = log 2 − x + 1 即 f x =− log 2 − x + 1 , 又 f 0 = 0,∴f x =log 2 x + 1 ,x〉00,x = 0 ， − log 2 1 − x ,x〈0（2）∵x > 0 时 ：f x = log 2 x + 1 > 0,f 0 = 0,∴f m <− 2⇔− log 1 − m <− 2,∴log 2 1 − m > 2,⎪x ∴1 − m > 4,∴m <− 3.【点睛】本题主要考查函数解析式的求解，奇函数的性质及其应用等知识，意在考查学生的转化能力和计算求解能力.【变式演练 5】已知函数 ƒ x = 4x −a 是奇函数．2（1） 求实数 a 的值；（2） 用定义证明函数 ƒ x 在 R 上的单调性；（3） 若对任意的 x ∈ R ，不等式 ƒ(x 2 − x 等+ ƒ(2x 2 − ݇等 > 0 恒成立，求实数 ݇ 的取值范围．【答案】（1）a = 1（2）见解析（3）݇ <− 112【解析】（1）∵函数 ƒ x 的定义域为 R ，且 ƒ x 是奇函数，∴ƒ 0 = 0，解得 a = 1．此时 ƒ x = 2x − 2−x ，满足 ƒ − x =− ƒ x ，即 ƒ x 是奇函数．∴a = 1．（2）任取x 1,x 2 ∈ − œ, + œ ，且x 1 < x 2，则2x 1 < 2x 2 ，( 1 等x 1 > ( 1 等x 2 ，22于是 ƒ(x 1等− ƒ(x 2等 = 2x 1 − 1 − 2x x 2 + 1 = 2x 1 − 2x 2 + ( 1 等x 2 − ( 1 等x 1 < 0，2x 12x 22 2即 ƒ(x 1等 < ƒ(x 2等，故函数 ƒ x 在 − œ, + œ 上是增函数．（3）由 ƒ(x 2 − x 等 >− ƒ(2x 2 − ݇等及 ƒ x 是奇函数，知 ƒ(x 2 − x 等 > ƒ(݇ − 2x 2等，又由 ƒ x 在 − œ, + œ 上是增函数，得x 2 − x > ݇ − 2x 2，即 ݇ < 3x 2 − x 对任意的 x ∈ R 恒成立，∵当 x = 1时，3x 2 − x 取最小值− 1 ，∴݇ <− 1 ．61212考点：函数的简单性质的综合运用．【高考再现】⎨-2 ≤ x -1 ≤ 0或x -1 ≥ 2 ⎩1. 【2020 年高考江苏卷 7】已知 y =2f ( x ) 是奇函数，当 x ≥ 0 时， f (x ) = x 3，则 f (-8) 的值是．【答案】 -422【解析】 y = f ( x ) 是奇函数，当 x ≥ 0 时， f (x ) = x 3，则 f (-8) = - f (8) = -83 = -4 ．【专家解读】本题考查了函数的奇偶性，考查数学运算学科素养．解题关键是正确应用函数的奇偶性．2. 【2020 年高考山东卷 8】若定义在 R 上的奇函数 f (x ) 在(-∞, 0) 单调递减，且 f (2) = 0 ，则满足 xf (x -1) ≥ 0的 x 的取值范围是（ ）A ． [-1 , 1] [3 , + ∞)B ． [-3 , -1] [0 , 1]C ． [-1 , 0] [1 , + ∞)D ． [-1 , 0] [1 , 3]【答案】D【思路导引】首先根据函数奇偶性与单调性，得到函数 f (x ) 在相应区间上的符号，再根据两个数的乘积大于等于零，分类转化为对应自变量不等式，最后求并集得结果．【解析】因为定义在 R 上的奇函数 f (x ) 在(-∞, 0) 上单调递减，且 f (2) = 0 ，所以 f (x ) 在(0, +∞) 上也是单调递减，且 f (-2) = 0 ， f (0) = 0 ，所以当 x ∈(-∞, -2) ⋃ (0, 2) 时， f (x ) > 0 ，当 x ∈(-2, 0) (2, +∞) 时， f ( x ) < 0 ，所以由 xf (x -1) ≥ 0 可得： ⎧x < 0 ⎩ ⎧x > 0 或⎨0 ≤ x -1 ≤ 2或x -1 ≤ -2 或 x = 0解得-1 ≤ x ≤ 0 或1 ≤ x ≤ 3 ，所以满足 xf (x -1) ≥ 0 的 x 的取值范围是[-1 , 0] [1 , 3]，故选 D ．【专家解读】本题的特点是注重函数性质的应用，本题考查了函数的奇偶性、单调性，考查抽象不等式的 解法，考查分类讨论、数形结合、转化与化归等思想方法，考查数学运算、直观想象、数学建模等学科素 养．解题关键是正确应用函数的性质，转化为不等式组来求解．3. 【2017 全国二文】已知函数 f (x ) 是定义在 R 上的奇函数，当 x ∈ (-∞, 0) 时， f (x ) = 2x3+ x 2 ,则 f (2) =2【答案】12【解析】 f (2) = - f (-2) = -[2 ⨯ (-8) + 4] = 12【考点】函数奇偶性【名师点睛】(1)已知函数的奇偶性求函数值或解析式，首先抓住奇偶性讨论函数在各个区间上的解析式， 或充分利用奇偶性得出关于 f (x ) 的方程，从而可得 f (x ) 的值或解析式.(2)已知函数的奇偶性求参数，一般采用待定系数法求解，根据 f ( x ) ± f (- x ) = 0 得到关于待求参数的恒等 式，由系数的对等性得参数的值或方程(组)，进而得出参数的值.4. 【2018 年全国普通高等学校招生统一考试文科数学】已知是定义在 R 上的偶函数，且在区间上单调递增，若实数 满足，则 的取值范围是A ．B ．C ．D ．【答案】C【解析】由题意得a -1a -11a -11 1 3f (-2) > f (- 2 )⇒ -2 > - ⇒ 2< 22⇒ a -1 < ⇒ < a < ，2 2 2故选 C【考点】利用函数性质解不等式【名师点睛】不等式中的数形结合问题，在解题时既要想形又要以形助数，常见的“以形助数”的方法有：（1） 借助数轴，运用数轴的有关概念，解决与绝对值有关的问题，解决数集的交、并、补运算非常有效．（2） 借助函数图象性质，利用函数图象分析问题和解决问题是数形结合的基本方法，需注意的问题是准确 把握代数式的几何意义实现“数”向“形”的转化．5. 【2018 年全国普通高等学校招生统一考试理数】已知 f(x 等是定义域为( − œ, + œ等的奇函数,满足 f(1 − x 等 =f(1 + x等.若f(1等 = 2，则f(1等+ f(2等+ f(3等+ ⋯ + f(50等 =（）A．− 50 B．0 C．2 D．50【答案】C【解析】因为f(x等是定义域为( − œ, + œ等的奇函数，且f(1 − x等= f(1 + x等，所以f(1 + x等=− f(x − 1等∴ f(3 + x等=− f(x + 1等= f(x − 1等∴ T = 4,因此f(1等+ f(2等+ f(3等+ ⋯ + f(50等 = 12[f(1等+ f(2等+ f(3等+ f(4等] + f(1等+ f(2等，因为f(3等=− f(1等，f(4等=− f(2等，所以f(1等+ f(2等+ f(3等+ f(4等 = 0，∵f(2等=f( −2等=−f(2等∴ f(2等=0，从而f(1等+ f(2等+ f(3等+ ⋯+f(50等=f(1等=2，选 C.点睛：函数的奇偶性与周期性相结合的问题多考查求值问题，常利用奇偶性及周期性进行变换，将所求函数值的自变量转化到已知解析式的函数定义域内求解．6.【2015 高考广东，理3】下列函数中，既不是奇函数，也不是偶函数的是（）A.y =x +e xB.y =x +1xC.y = 2x +12xD.y =【答案】A ．【考点定位】函数的奇偶性判断．【名师点睛】本题主要考查函数的奇偶性判断和常见函数性质问题，但既不是奇函数，也不是偶函数的判断可能较不熟悉，容易无从下手，因此可从熟悉的奇偶性函数进行判断排除，依题易知B 、C 、D 是奇偶函数，排除得出答案，属于容易题．【反馈练习】1+x21．（多选）【海南省2021届高三年级第二次模拟考试】下列函数中是偶函数，且在区间(0,1)上单调递增的是（）A.y =x2 -2B.y =2 xC.y =| x | +1| x |D.y=x 2| x |【答案】AD【分析】利用函数的奇偶性的定义判断奇偶性，根据函数解析式判断单调性.【详解】A，因为f(-x)=(-x)2-2=x2-2=f(x )，y =x2 - 2 是偶函数，在区间(0,1) 上为增函数，符合题意；B，因为f (-x)=2=-2=-f (x)，y =2 是奇函数，且在区间(0,1) 上为减函数，不符合题意；-xC，因为f (-x)=| -x | +x x1=| x | +1=f (x)，y =| x | +1 (x ≠ 0) 是偶函数，当x ∈(0,1) 时，y= x +1 | -x | | x | | x | x单调递减，不符合题意；x2 x2 x2D，因为f (-x )===f (x )，y =| -x | | x | | x |(x ≠ 0) 是偶函数，且在区间(0,1) 上为增函数，符合题意.故选：AD2.【安徽省淮北市2020-2021 学年高三上学期第一次模拟考试文科】设函数g (x)=f (x )+x 2 是定义在R 上的奇函数，且F (x)=f (x)+3x ，若f (1)=1，则F (-1)=（）A.-43B.-73C．-8D．13 3【答案】C【分析】根据g (x)是奇函数，可得f (-x )+f (x )=-2x 2 ，即可求出f (-1)=-3 ，进而可求F (-1).【详解】g (x )是奇函数，∴g (-x)=-g (x)，即f (-x )+x 2 =-f (x )-x 2 ，即f (-x )+f (x )=-2x 2 ， f (1)=1 ，∴f (-1)=-3 ，∴F(-1)= f (-1)+ 3-1 =-3 + 3-1 =-8 .3故选：C.3.【河南省郑州市2020-2021 学年高三上学期第一次质量检测文科】设f (x )是R 上的奇函数且满足f (x-1)=f (x +1)，当0 ≤x ≤1时，f (x)= 5x (1-x )，则f (-2020.6)=（）21 7 A．B．25 10 C.-85D.-65【答案】D【分析】由题意可知，f (x)是以2 为周期的周期函数，进而可得出f (-2020.6)=f (-0.6 )，再利用奇函数的性质可求得结果.【详解】对任意的x ∈R ，f (x -1)=f (x +1)，即f (x)=f (x + 2)，所以，函数f (x )是以2 为周期的周期函数，∴f (-2020.6)=f (-0.6)，由于函数f (x )为R 的奇函数，且当0 ≤x ≤ 1时，f (x )= 5x (1-x )，因此，f (-2020.6)=f (-0.6)=-f (0.6)=-5⨯ 0.6⨯(1- 0.6)=-6 .5故选：D.【点睛】方法点睛：函数的三个性质：单调性、奇偶性和周期性，在高考中一般不会单独命题，而是常将它们综合在一起考查，其中单调性与奇偶性结合、周期性与抽象函数相结合，并结合奇偶性求函数值，多以选择题、填空题的形式呈现，且主要有以下几种命题角度；（1）函数的单调性与奇偶性相结合，注意函数的单调性及奇偶性的定义，以及奇、偶函数图象的对称性．（2）周期性与奇偶性相结合，此类问题多考查求值问题，常利用奇偶性及周期性进行交换，将所求函数值的自变量转化到已知解析式的函数定义域内求解；（3）周期性、奇偶性与单调性相结合，解决此类问题通常先利用周期性转化自变量所在的区间，然后利用奇偶性和单调性求解.4.【山东省淄博市2021 届高三上学期教学质量摸底检测（零模）】已知定义在R 上的奇函数f (x )满足f (x)=f (2 -x )，且在[-1, 0)上有f (x)= 4x ，则f (2020.5)=（）A．2 B．12C.-2D.-12【答案】D【分析】根据题意可得函数f (x)是周期为4 的周期函数，结合函数为奇函数可得f (2020.5)=-f (-0.5) ，代入函数解析式化简即可.【详解】解：因为定义在R 上的奇函数f (x)满足f (x)=f (2 -x )，所以f (2 +x )=f (-x )=-f (x) ，所以f (2 +(2 +x ))=-f (2 +x) =-(-f (x))= f (x) ，即函数f (x )是周期为4 的周期函数，又x ∈[-1, 0)时有f (x)= 4x ，所以f (2020.5)=f (0.5) =-f (-0.5) =-4-0.5 =-1 2故选：D.【点睛】函数的单调性与奇偶性的综合问题解题思路：(1)解决比较大小、最值问题应充分利用奇函数在关于原点对称的两个区间上具有相同的单调性，偶函数在关于原点对称的两个区间上具有相反的单调性；(2)解决不等式问题时一定要充分利用已知的条件，把已知不等式转化成f (x1 ) >f (x2 ) 或f (x1 ) <f (x2) 的形式，再根据函数的奇偶性与单调性，列出不等式(组)，要注意函数定义域对参数的影响.5.【云南省昆明市官渡区2021 届高三上学期两校联考】若定义在R 上的函数f (x )满足f (-x) =f (x) ，f (2 -x) = f ( x) ，且当x ∈[0,1] 时，f (x) =H (x) =xe x-f (x) 在区间[-5,1] 上的零点个数为（）A．4 B．6 C．8 D．10【答案】B【分析】先分析函数H (x) =xe x-f (x) 的零点个数，即y = f (x) 与y = xe x在区间[-5,1] 上的交点个数，再分析函数周期性、对称性和单调性画函数图象，看图即得结果.【详解】依题意，函数H (x) =xe x-f (x) 的零点个数，即y = f (x) 与y = xe x在区间[-5,1] 上的交点个数，学习界的007定义在 R 上的函数 f (x )满足 f (−x )=f (x )，f (2−x )=f (x )，∴函数 f (x )是偶函数，且函数的图象关于 x =1 对称，故 x ∈[0,1]， f (x ) =1x 2+ y 2= 1 ，故函 数 f (x )是单位圆的 4，利用周期性和对称性可得函数图像.设 g (x )=xe x ，其定义域为 R ，g ′(x )=(xe x )′=x ′e x +x (e x )′=e x +xe x令 g ′(x )=0，得：x =−1，且 x < -1时 g ′(x )<0， x > -1 时 g ′(x ) >0，故函数 g (x )=xe x 的单调递减区间为(−∞,−1)，单调递增区间为(−1,+∞)，当 x =−1 时，函数 g (x )=xe x 的极小值为 g (-1) = - 1，且 x < 0 时 g (x )<0， x > 0 时 g (x ) >0，故作图如下：e将 x 轴下方部分图像对称到上方，即得 y = xe x图像，要求 y = f (x ) 与 y =xe x在区间 [-5,1] 上的交点个数，则作图如下：1- x 2⎣ ⎦⎩结合图像可知，有 6 个交点，故函数 H (x ) = xe x- f (x ) 有 6 个零点.故选：B.【点睛】“以形助数”是已知两图象交点问题求参数范围常用到的方法，解决此类问题的关键在于准确作出不含参数的 函数的图象，并标清一些关键点，对于含参数的函数图象要注意结合条件去作出符合题意的图形．6【. 2021 届全国著名重点中学新高考冲刺】已知定义在 R 上的函数 y = f (x + 1)- 3 是奇函数，当 x ∈(1, +∞)时， f '(x ) ≥ x + 1- 3 ，则不等式⎡ f ( x ) - 3⎤ ln (x +1) > 0 的解集为（ ）x -1A ． (1, +∞)B ． (-1, 0) ⋃ (e , +∞)C ． (0,1) (e , +∞)D ． (-1, 0) ⋃ (1, +∞ )【答案】D【分析】本题首先可根据题意得出函数 f ( x ) 的图像关于点(1, 3) 中心对称且 f (1) = 3 ，然后根据基本不等式得出f '( x ) ≥ 0 ，则函数 f ( x ) 在 R 上单调递增，最后将不等式⎡ f ( x ) - 3⎤ ln (x +1) > 0 转化为 ⎪⎧ f ( x ) - 3 > 0 或 ⎣ ⎦⎨⎪ln ( x +1) > 0⎩⎧⎪ f ( x ) - 3 < 0⎨⎪ln ( x +1) < 0 ，通过计算即可得出结果.【详解】因为函数 y = f (x + 1)- 3 是定义在 R 上的奇函数，所以函数 f ( x ) 的图像关于点(1, 3) 中心对称，且 f (1) = 3 ，当 x ∈(1, +∞) 时， x -1 > 0 ，则 x +1 x -1 - 3 = (x -1)+ 1 x -1- 2 ≥2 = 0 ，当且仅当 x = 2 时取等号，故 f '(x ) ≥ x + 1x -1- 3 ≥ 0 ，函数 f ( x ) 在(1, +∞) 上单调递增，因为函数 f ( x ) 的图像关于点(1, 3) 中心对称，所以函数 f ( x ) 在 R 上单调递增，⎧⎪ f ( x ) - 3 > 0 ⎧⎪ f ( x ) - 3 < 0不等式 ⎡⎣ f ( x ) - 3⎤⎦ ln (x +1) > 0 可化为⎨ln ( x +1) > 0 或⎨ln ( x +1) < 0 ，⎪⎩ ⎪⎩⎧⎪ f ( x ) - 3 > 0 ⎧x > 1 ⎨ln ( x +1) > 0 ，即⎨x > 0 ，解得 x > 1 ，⎪⎩⎩⎧⎪ f ( x ) - 3 < 0 ⎧x < 1 ⎨ln ( x +1) < 0 ，即⎨-1 < x < 0 ，解得-1 < x < 0 ， ⎩⎪ ⎩故不等式的解集为(-1, 0) ⋃ (1, +∞ ) ，故选：D. 【点睛】关键点点睛：若函数 y = f ( x + a )(a ∈ R ) 是偶函数，则函数 y = f (x ) 的图像关于直线 x = a 对称；若函数y = f ( x + b )(b ∈ R )是奇函数，则函数 y = f (x ) 的图像关于点(b , 0) 中心对称，考查通过基本不等式求最值，考查根据导函数判断函数单调性，是难题.7【. 安徽省安庆市怀宁中学 2020-2021 学年高三上学期第一次质量检测理科】已知定义在 R 上的奇函数 f ( x ) ， 对任意的实数 x ，恒有 f ( x + 3) = - f (x ) ，且当x ∈(0, 3] 时， f ( x ) = x 2 - 6x + 8 ，则 2 f (0) + f (1) + f (2) +... + f (2020) = （ ）A ．6B ．3C ．0D ． -3【答案】B【分析】根据函数 f ( x ) 恒有 f ( x + 3) = - f (x ) ，得到函数 f (x ) 的周期是 6，再由 f ( x ) 定义在 R 上的奇函数，得到 f (0) = 0, f (3) = 0 ，然后f (0) + f (1) + f (2) +... + f (2020) = ⎣⎡ f (0) + f (1)+ f (2 )+ ... + f + f (0) + f (1) + f (2) + f (3) + f (4) 求解.【详解】因为函数 f ( x ) 对任意的实数 x ，恒有 f (x + 3) = - f (x ) ， (5 )⎤⎦ ⨯ 336所以 f ( x + 6) = - f (x + 3)= f (x ) ，所以函数 f (x ) 是以 6 为周期的周期函数， 又 f (x ) 定义在 R 上的奇函数， 所以 f (0) = 0, f (3) = - f (0) = 0 ，又当 x ∈(0, 3] 时， f ( x ) = x 2- 6x + 8 ，2所以 f (1) = 3, f (2) = f (-1+ 3) = - f (-1) = f (1) = 3 ，f (4) = f (1+ 3) = - f (1) = -3, f (5) = f (2 + 3) = - f (2) = -3 ， 所以 f (0) + f (1) + f (2) +... + f (2020) ， = ⎣⎡ f (0) + f (1)+ f (2 )+ ... + f (5 )⎦⎤ ⨯ 336+ f (0) + f (1) + f (2) + f (3) + f (4) ，= 0⨯ 336 + 3 = 3 ，故选：Bx 3 + sin x8. 【山东省枣庄三中 2021 届高三 10 月份第二次质检】函数 f ( x )=e x + e- x的图象大致是（ ）A ．B ．C ．D ．【答案】A【分析】判断函数为奇函数，由图像可排除 C ，D ；然后利用特殊值，取 x = π，可排除 B.)【详解】定义域为 R ，定义域关于原点对称，f (-x ) = (-x )3+ sin (-x ) e - x + e x= - x 3 + sin x e x + e- xf ( x ) 是奇函数，排除 C ，D ；x = ππ3 + sin ππ3当时， f ( x ) =e π + e -π =e π+ e-π> 0 ，排除 B ；故选：A.9. 【湖北省“荆、荆、襄、宜“四地七校联盟 2020-2021 学年高三上学期期中联考】若函数f (x ) = sin x ⋅ ln(ax 的图象关于 y 轴对称，则实数a 的值为（ ）A ．2B ． ±2C ．4D ． ±4【答案】B【分析】根据图象对称关系可知函数为偶函数，得到 f ( x ) = f (-x ) ，进而得到 ax=立，根据对应项系数相同可得方程求得结果.【详解】f ( x) 图象关于 y 轴对称，即 f ( x) 为偶函数 ∴ f ( x ) = f (-x )即：sin x ⋅ l n (ax += -sin x ⋅ l n ax = sin x ⋅ l n 1ax∴ a x1恒成立，即：1+ 4x 2 - a 2 x 2 = 1ax=，2∴ a 2 = 4 ，解得： a = ±2本题正确选项： B10. 【广西南宁市普通高中 2021 届高三 10 月摸底测试数学（文）】已知函数 f (x ) =2x - a2x+1是 R 上的奇函数，当a ∈(0,π) 时，不等式 f ( x sin x -1) + f (cos x - b ) ≤ 0 恒成立，则整数b 的最小值为（）A ．1B ．2C ．3D ．4【答案】A【分析】由题意有 f (0) = 0 ，即可得 f (x ) = 1-2 2x+1，进而可知其为增函数，由不等式恒成立结合 f (x ) 的单调性 有 x sin x + cos x ≤ b +1 ，令 g (x ) = x sin x + cos x 利用导数研究 g (x ) 的最值，即可求b 的取值范围，可得最小值. 【详解】由题意知： f (0) = 0 ，即1- a = 0 ，所以 a = 1 ，22x -1 2∴函数 f (x ) = 2x +1 = 1- 2x +1为 R 上的增函数，不等式 f (-x ) = - f (x ) ，f ( x sin x -1) + f (cos x - b ) ≤ 0恒成立，又∴ f ( x sin x -1) ≤ - f (cos x - b ) ，得 f (x sin x -1) ≤ f (b - cos x ) ，即 x sin x + cos x ≤ b +1 ，令 g (x ) = x sin x + cos x ， g '(x ) = x cos x ，当 x ∈⎛ 0,π⎫时， g '( x ) > 0 ， g (x ) 单调递增；当 x ∈⎛ π,π⎫2 ⎪ 2 ⎪ ⎝ ⎭⎝ ⎭时， g '( x ) < 0 ， g (x ) 单调递减，∴当 x = π时， g ( x ) 取极大值也是最大值，最大值为 g⎛ π⎫ = π， ⎪ 2⎝ ⎭ 2即b ≥π-1，又b ∈Z ，有b =1.2 min故选：A。

四川省泸州市2021 2021学年高三数学一诊试卷（文科）Word版含解四川省泸州市2021-2021学年高三数学一诊试卷（文科）word版含解四川省泸州市2022-2022学年高三试卷（文科数学）一、多项选择题（每个子题5分，共50分。

每个子题给出的四个选项中只有一个符合问题要求）1。

设置a={x | x2x≤ 0}，B={0，1，2}，然后是a∩ B=（）A？b、{0}C.{0，1}D.{0，1，2}2。

复数z=a.1b．（I是一个虚单位），然后| Z |=（）Cd．2)图像的对称轴方程为（）d．x=π3.函数f（x）=sin（x+a.x）=b．x=c、 x=4．某程序框图如图所示，若运行该程序后输出s=（）a、不列颠哥伦比亚省。

5．某校高三年级共1500人，在某次数学测验后分析学生试卷情况，需从中抽取一个容量为500的样本，分层抽样，120分以上100人，90~120分250人。

那么在这个测试中得分低于90分的人数是（）a.600b。

450摄氏度。

300天。

1506．若某四面体的三视图是全等的等腰直角三角形，且其直角边的长为6，则该四面体的体积是（）a．108b．72c．36d．97.是单位向量，|+2 |=，那么向量的夹角是（）A.30°b.45°c.60°d.90°8．实数x、y满足，这z=3x+4y，则z的取值范围是（）a、 [1,25]B[4,25]C[1,4]D[5,24]9。

下面的命题是正确的（）a．“b2=ac”是“a，b，c成等比数列”的充要条件b．“?x∈r，x2＞0”的否定是“?x0∈r，x02＞0”c、“如果a=4，那么函数f（x）=AX2+4x1只有一个零点”的逆命题是真命题D。

“函数f（x）=lnx2和函数g（x）=的图象相同”10.已知两个方程x2+（1+a）x+1+a+B=0（a，B）∈ R）大约X分别是X1和X2，并且0<X1<1<X2，那么X的值范围是（）ab．c。

2021届四川省泸州市高三上学期文科数学第一次教学质量诊断性试题答案13．3；14．0；15.43-；16三、解答题：17．解：（Ⅰ）因为2()2cos 12x f x x =-+cos x x =- ·················································································· 1分 2sin()6x π=-， ··················································································· 2分因为()()6f παα=+，所以sin()6παα-=， ······························· 3分1cos 2ααα-=，·························································· 4分即cos αα-=， ·········································································· 5分所以tan α=··············································································· 6分 （Ⅱ）()f x 图象上所有点横坐标变为原来的12倍得到函数()g x 的图象，所以函数()g x 的解析式为()2sin(2)6g x x π=-， ········································· 8分因为02x π≤≤，所以52666x πππ--≤≤， ··········································· 9分 所以1()2g x -≤≤， ········································································· 11分故()g x 在[0,]2π上的值域为[1,2]-． ·························································· 12分18．解：（Ⅰ）因为()sin cos f x k x kx x '=+， ··································································· 2分所以()sin cos 2222f k k k ππππ'=+⨯=， ·························································· 3分又因为()sin 2222kf k b b ππππ=⨯+=+， ························································ 4分点(,())22f ππ处的切线方程为230x y --=．所以2k =, ····························································································· 5分 3b =-；································································································ 6分 （Ⅱ）()f x 在(0,)2π上有且只有一个零点， ························································ 7分因为()2sin 2cos f x x x x '=+， ··································································· 8分当(0,)2x π∈时，()0f x '>， ······································································ 9分所以()f x 在(0,)2x π∈上为单调递增函数且图象连续不断， ···························· 10分因为(0)30f =-<，()302f ππ=->， ······················································· 11分所以()f x 在(0,)2π上有且只有一个零点． ··················································· 12分19························································ 2分因为sin 0C ≠，所以sin cos 2AA =， ···························································· 3分······································································· 4分cos 02A≠，······················································································ 5分······································································· 6分 （Ⅱ）解法一：设ABD △的AB 边上的高为1h ，ADC △的AC 边上的高为2h ，因为3,3,1ABD ADC S S c b ===△△， ································································ 7分所以1211322c h b h ⋅=⨯⋅， ·········································································· 8分所以12h h =，AD 是ABC △角A 的内角平分线，所以30BAD ∠=， ·················· 9分 因为3ABD ADC S S =△△，可知34ABD ABC S S =△△， ·············································· 10分所以131sin 30sin 60242AB AD AB AC ⨯⨯=⨯⨯⨯， ·········································· 11分所以33AD =. ···················································································· 12分解法二：设=(0)3BAD παα∠<<，则=3DAC πα∠-， ························································ 7分 因为3ABD ADC S S =△△，3,1c b ==，所以11sin 3sin()223c AD b AD παα⨯⨯=⨯⨯⨯-， ·· 8分 所以sin sin()3παα=-， ······························· 9分 所以31sin cos sin 2ααα=-，3tan α∴=， 因为03πα<<，所以30BAD ∠=， ························································· 10分 3ABD ADC S S =△△，可知34ABD ABC S S =△△， ····················································· 11分所以131sin 30sin 60242AB AD AB AC ⨯⨯=⨯⨯⨯， 所以33AD =. ···················································································· 12分解法三：设AD x =，=BDA α∠，则=ADC πα∠-，在ABC △中，由3,1c b ==及余弦定理可得：2222cos a b c bc A =+-，所以7a =， ························································································ 7分 因为3ABD ADC S S =△△，可知373=BD DC =， ··············································· 8分在ABD △中2222cos AB BD AD BD AD α=+-⋅⋅， 即263379cos 16AD AD α=+-⋅⋅， ····························································· 9分 在ADC △中，2771cos()16AD AD πα=+-⋅⋅-， ······································· 10分 即2771+cos 16AD AD α=+⋅⋅， ······························································· 11分 所以33AD =． ················································································· 12分 20.解：（Ⅰ）第一步：在平面ABCD 内作GH ‖BC 交CD 于点H ； ······································· 2分第二步：在平面SCD 内作HP ‖SC 交SD 于P ；········································· 4分第三步：连接GP ，点P 、GP 即为所求． ······················································· 5分 （Ⅱ）因为P 是SD 的中点，//HP SC ，所以H 是CD 的中点，而//GH BC ，所以G 是AB 的中点， ················································································ 6分所以1sin1202GBC S BC GB ︒=⋅⋅=△， 连接AC ，GD 交于O ，连SO ，设S 在底面ABCD 的射影为M ， 因为SA SB SD ==，所以MA MB MD ==， ································ 7分 即M 为ABD △的外心，所以M 与O 重合， ····································· 8分因为OD 2SD =，所以SO ， ········································ 9分所以13S GBC GBC V S SO -=⋅⋅△ ················· 10分 因为GP //平面SBC ， ································· 11分所以S PBC P SBC G SBC S GBC V V V V ----====． ··················································· 12分 21.解：（Ⅰ）当52m =时，152)ln 2(5x x x f x =---， ·························································· 1分 所以()22215252122x x f x x x x -+'=+-=， ························································ 2分 因为0x >,由()0f x '>得22520x x -+>， ·································································· 3分 所以102x <<，或2x >， 所以()f x 在[1,2)上单减，(2,e]上单增， ······················································ 4分 所以函数()f x 在[1,e]上的最小值为51ln 22--； ············································· 5分 （Ⅱ）原不等式()1ln ln m x x x x nk x+-++⇔≤. ····················································· 6分因[]1,e m ∈,[],e 1x ∈,所以()1ln ln 1ln ln m x x x x nx x x x nxx+-+++-++≥,令()1ln ln x x x x ng x x +-++=, ···································································· 7分即()2ln x x n g x x -+-'=，令()ln p x x x n =-+-，即()11p x x '=-+， 所以()p x 在[],e 1x ∈上递增； ····································································· 8分 ①当()10p ≥即1n ≤时, 因为[]1,e n ∈,所以1n =，当[],e 1x ∈,()0p x ≥,即()0g x '≥，所以()g x 在[]1,e 上递增， 所以()()min 1c g x g n ===，故22n c n +==， ··············································································· 9分 ①当()e 0p ≤即[]e 1,e n ∈-时， 因为[],e 1x ∈,()0p x ≤,即()0g x '≤，所以()g x 在[]1,e 上递减，所以()()min 2e en c g x g +===， 故212e ,e 1e ee n n c n +⎡⎤+=+∈+++⎢⎥⎣⎦ ······················································· 10分 ①当()()1e 0p p <即()1,1n e ∈-时, 又()ln p x x x n =-+-在[]1,e 上递增，所以存在唯一实数()01,e x ∈,使得()00p x =,即00ln n x x =-，则当()01,x x ∈时()0p x <，即()0g x '<，当()0,e x x ∈时()0p x >即()0g x '>， 故()g x 在()01,x x ∈上减，()0,e x x ∈上增， 所以()()00000mi 000n 1ln ln 1ln x x x x n x x x c g x g x +-++=+===.························· 11分所以00000011ln ln n c x x x x x x +=++-=+， 设()001x x x u =+（()01,e x ∈），则()2'02001110x u x x x -=-=>， 所以()u x 在[]1,e 上递增,所以12,e e n c ⎛⎫+∈+ ⎪⎝⎭.综上所述22,e 1e n c ⎡⎤+∈++⎢⎥⎣⎦. ·································································· 12分 22.解： (Ⅰ) 解法一：设曲线1C 与过极点且垂直于极轴的直线相交于异于极点的点E ，且曲线1C 上任意点F (,)ρθ，边接OF ，EF ，则OF ⊥EF ， ·············································· 2分在△OEF 中，4cos()4sin 2πρθθ=-=， ······················································ 4分解法二：曲线1C 的直角坐标方程为22(2)4x y +-=， ······································ 2分即2240x y y +-=， 所以曲线1C 的极坐标方程为4sin ρθ=； ·························· 4分（Ⅱ）因曲线2C的参数方程为)4x ty t π⎧=⎪⎨=-⎪⎩与两坐标轴相交，所以点(2,0),(0,2)A B ， ············································································ 6分 所以线段AB 极坐标方程为cos sin 20(0)2πρθρθθ+-=≤≤， ·························· 7分12||sin cos OP ρθθ==+，2||4sin OM ρθ==,sin cos 4sin 2OMOP θθθ+=⨯ 22sin 2sin cos θθθ=+······················ 8分 1cos2sin2θθ=-+)14πθ=-+， ······················································ 9分 当38πθ=1． ··························································· 10分 23.解：(Ⅰ)由3222,ab a b =++≥ ······································································· 2分220-≥，， ··························································· 4分 当且仅当1,2a b ==时取得“=，即k 的最小值为2． ···················································································· 5分（Ⅱ）由2k =，2()(2)2x m x x m x m -+-≥---=-， ·········································· 7分因0,x R ∃∈使不等式22x m x -+-≤成立， 所以22,m -≤即222m -≤-≤， ····················································································· 9分 即m 的取值范围是[0,4] ············································································ 10分。

泸州老窖高2021级高三上期一诊模拟(二)数学（文科）（答案在最后）第Ⅰ卷(选择题，共60分）一、选择题本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}1,2,3,4A =，{}|2B x x =≤，则A B = （）A.{}1 B.{}1,2 C.{}1,2,3 D.{}1,2,3,4解：由题意知A B = {}1,2.故选：B2.已知34a =，2log 3b =，则ab =（）A .2 B.9C.4D.5解：因为34a =，所以3log 4a =，所以322lg 2lg 3log 4log 32lg 3lg 2ab =⨯=⨯=.故选：A3．设l 是直线，α，β是两个不同的平面，则下列命题正确的是（）A ．若l ∥α，l ∥β，则α∥βB ．若l ∥α，l ⊥β，则α⊥βC ．若α⊥β，l ⊥α，则l ∥βD ．若α⊥β，l ∥α，则l ⊥β解：对于A 选项，设α∩β＝a ，若l ∥a ，且l ⊄α，l ⊄β，则l ∥α，l ∥β，此时α与β相交，故A 选项错误；对于B 选项，l ∥α，l ⊥β，则存在直线a ⊂α，使得l ∥a ，此时a ⊥β，由平面与平面垂直的判定定理得α⊥β，故B 选项正确；对于C 选项，若α⊥β，l ⊥α，则l ∥β或l ⊂β，故C 选项错误；对于D 选项，若α⊥β，l ∥α，则l 与β的位置关系不确定，故D 选项错误．选B.答案：B4.当某种药物的浓度大于100mg/L（有效水平）时才能治疗疾病，且最高浓度不能超过1000mg/L （安全水平）．从实验知道该药物浓度以每小时按现有量14%的速度衰减．若治疗时首次服用后的药物浓度约为600mg/L ，当药物浓度低于有效水平时再次服用，且每次服用剂量相同，在以下给出的服用间隔时间中，最合适的一项为（）（参考数据：lg 20.301≈，lg 30.477≈，lg86 1.935≈）A.4小时 B.6小时 C.8小时 D.12小时【分析】设n 小时后药物浓度为()160010.14n y -=⨯-，由题意可得()160010.14100n -⨯-<，两边取常用对数求解即可.解：设n 小时后药物浓度为()160010.14n y-=⨯-若n 小时后药物浓度小于100mg/L ，则需再服药.由题意可得()160010.14100n -⨯-<，即110.866n -<所以()1lg 0.86lg 6n -<-，则lg 6lg 2lg 30.3010.4770.778111.969lg 0.86lg 86lg100 1.93520.065n -++->=-=-=≈--所以12.969n >所以在首次服药后13个小时再次服药最合适，则服用药物的间隔时间12小时最合适故选：D5.已知命题p ：函数()af x x =在()0,∞+上单调递减；命题:q x ∀∈R ，都有220ax x a -+≤．若p q ∨为真命题，p q ∧为假，则实数a 的取值范围为（）A .()1,0- B.[]0,1C.(]()10,-∞-+∞ , D.(](),11,-∞-⋃+∞解：若命题p 为真，则a<0，若q 为真，则201440a a a <⎧⇒≤-⎨∆=-≤⎩，由于p q ∨为真命题，p q ∧为假，则,p q 中一真一假若p 真q 假，则满足：0101a a a <⎧⇒-<<⎨>-⎩；若q真p 假，则满足：01a a ≥⎧⎨≤-⎩，此时a 无解，综上10a -<<故选：A 6.已知π3sin 63α⎛⎫+= ⎪⎝⎭，则2πcos 23α⎛⎫-= ⎪⎝⎭（）A.13-B.13C.33- D.33解：因为22πππ31cos 2=cos212sin 1236633ααα⎛⎛⎫⎛⎫⎛⎫++=-+=-⨯= ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭，所以2πππ1cos 2cos π2cos 23333ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=-+=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦．故选：A.7．若1a b >>，01c <<，则（C）A ．c ca b <B ．c cab ba <C ．log log b a a c b c<D ．log log a b c c<解：用特殊值法，令a =3，b =2，12c =，可知选项A 错误；11223223⨯>⨯，选项B 错误；2313log 2log 22<，选项C 正确；3211log log 22>，选项D 错误.故选C.考点：指数函数与对数函数的性质8.如图，在ABC ∆中，3AB AC ==，1cos 3BAC ∠=-，D 是BC 的中点，以AD 为折痕把ACD △折叠，使点C 到达点C '的位置，则当三棱锥C ABD '-体积最大时，其外接球的表面积为（）A ．94πB ．52πC ．92πD ．5π且长方体的长、宽、高分别为1、2、2，设三棱锥C ABD '-外接球的半径为R ，则2222222(2)1(2)(2)5R DA DB DC '=++=++=.所以，三棱锥C ABD '-外接球的表面积为24π5πS R ==.故选D.9.将函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭的图象向右平移4π个单位长度后得到函数()g x 的图象，且()g x 的图象的一条对称轴是直线4x π=-，则ω的最小值为（）A ．32B ．72C ．2D ．3【分析】利用平移变换得出()sin 44g x x ωππω⎛⎫=-+⎪⎝⎭，再由对称轴的性质得出122k ω=--，Z k ∈，结合0ω>得出ω的最小值.解：将函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭的图象向右平移4π个单位长度后得到函数()g x 的图象对应的函数为()sin sin 4444g x x x ππωππωω⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦因为函数()g x 的图象的一条对称轴是直线4x π=-所以4442k ωπωππππ--+=+，Z k ∈解得122k ω=--，Z k ∈，又0ω>所以当1k =-时，ω取最小值，为32故选：A【点睛】关键点睛：解决本题的关键在于利用对称轴的性质结合0ω>得出ω的最小值.10．如图，某景区欲在两山顶A ，C 之间建缆车，需要测量两山顶间的距离．已知山高AB ＝3（km ），CD ＝33（km ），在水平面上E 处测得山顶A 的仰角为30°，山顶C 的仰角为45°，∠BED ＝150°，则两山顶A 、C 之间的距离为（）A ．63(km)B ．53(km)C(km)D(km)【分析】先计算BE ，DE ，利用余弦定理计算BD ，再利用勾股定理计算AC ．解：在Rt △ABE 中，∵AB＝，CD ＝3，∠AEB ＝30°，∠CED ＝45°，∴BE ＝3，DE ＝3，又∠BED ＝150°，∴BD ＝＝3，过A 作AF ⊥CD 于F ，则AF ＝BD ＝3，CF ＝CD ﹣AB ＝2，∴AC＝＝＝5（km ）．故选：B ．11.已知点P 是曲线()ln f x x x =上任意一点，点Q 是直线3y x =-上任一点，则PQ 的最小值为（）A．BC ．1D ．e【分析】利用导数的几何意义求出曲线的切线，利用数形结合进行求解即可.解：函数()ln f x x x =的定义域为全体正实数，()()ln ln 1f x x x f x x '=⇒=+，当1e x >时，()()0,f x f x '>单调递增，当10ex <<时，()()0,f x f x '<单调递减，函数图象如下图：过点()00,P x y 的曲线()ln f x x x =的切线与直线3y x =-平行时，PQ 最小，即有()()000ln 11101,0f x x x y P '=+=⇒=⇒=⇒，所以min PQ==故选：A12.若函数f (x )的定义域为R ，且f (2x +1)为偶函数，f (x –1)的图象关于点(3，3)成中心对称，则下列说法正确的个数为（）①f (x )的一个周期为2；②f (22)=3；③f (x )图象的一条对称轴为x =5；④191()57i f i ==∑.A ．1B ．2C ．3D ．4第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上．13.曲线e cos x y x =在0x =处的切线方程为_____．【答案】10x y -+=【分析】根据导数的几何意义即得.解：因为e cos x y x =，所以si e c s e n o x x y x x -⋅'⋅=，当0x =时，00e cos 0e sin 0=1y '=-⋅⋅，0co e s 01y ==，故切线方程为：()110y x -=⨯-，即10x y -+=.故答案为：10x y -+=.14．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为________．解：由正视图和俯视图可知几何体是正方体切割后的一部分(四棱锥C 1­ABCD )，还原在正方体中，如图所示．多面体最长的一条棱即为正方体的体对角线，如图即AC 1.由正方体棱长AB ＝2知最长棱AC 1的长为2 3.答案：2315.设当x θ=时，函数()sin 2cos f x x x =-取得最大值，则cos θ=___________．255-解：∵()f x =sin 2cos x x -5(sin cos )55x x -令cos ϕ=5，sin 5ϕ=-，则()f x cos sin cos )x x ϕϕ+)x ϕ+，当x ϕ+=2,2k k z ππ+∈，即x =2,2k k z ππϕ+-∈时，()f x 取最大值，此时θ=2,2k k z ππϕ+-∈，∴cos θ=cos(2)2k ππϕ+-=sin ϕ=5-.则下列结论中正确的有①//AF 平面1A DE③1A ，D ，E ，H 四点共面【答案】①③【分析】取1A D 的中点的中点N ，连接NG ，延长面1A DP 相交，可判断②；显然不成立可判断④.如上图，取1A D 的中点M ，连接AM //AM ，=EF AM ，则四边形⊄平面1A DE ，ME ⊂平面如上图，取11D C 的中点N ，连接NG ，延长DE 与11D C 交与点P ，连接1A P ，因为11//=A A NG A A NG ，，所以四边形1A AGN 是平行四边形，可得1//A N AG ，因为1A ∈平面1A DP ，N ∉平面1A DP ，所以直线1A N 与平面1A DP 相交，所以AG 与平面1A DE 相交，故②错误；如下图，连接EH ，则1//EH B C ，11//A D B C ，所以1//EH A D ，可得1A ，D ，E ，H 四点共面，故③正确；若1A ，D ，E ，1C 四点共面，则11//A D C E ，显然不成立，所以④错误.故填：①③.PAB，平面AEF，请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.作答时请写清题号.的极坐标；，代入三角形面积公式，结合三角恒等变换知识可化简得到30,2MOK ⎛⎤∈ ⎥⎝⎦.。

一、单选题二、多选题1. 一组样本数据的平均数为，标准差为.另一组样本数据，，…，的平均数为，标准差为.两组数据合成一组新数据，，…，，新数据的平均数为，标准差为，则（ ）A．B ．C．D ．与的大小与有关2. 已知过坐标原点的直线与函数的图象有且仅有三个公共点，若这三个公共点的横坐标的最大值为，则下列等式成立的是（ ）A．B．C．D．3. 已知，则“”是“”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4. 若，则下列结论不正确的是（ ）A．B．C．D．5. 已知双曲线的中点在原点，焦点，点为左支上一点，满足且，则双曲线的方程为（ ）A．B．C．D．6. 如图，正六边形的边长为2，取正六边形各边的中点，，，，，，作第二个正六边形；然后再取正六边形各边的中点，，，，，，作第三个正六边形；依此方法一直继续下去……，则第2022个正六边形的面积为（）A．B．C．D．7. 已知集合A={|﹣2≤x ≤3}，B ={x |y =}，则A ∩B =A ．{x |1＜x ≤3}B ．{x |x ≥﹣2}C ．{1，2，3}D ．{2，3}8. 为了绿色发展，节能减排，相关部门随机调查了10户居民今年二月份的用电量（单位：kW.h ），数据如下：1071017899881277423131156则该组数据的极差为（ ）A ．20B ．30C ．180D ．2009. 随着生活水平的不断提高，我国居民的平均身高也在增长.某市为了调查本市小学一年级男生身高情况，从某小学一年级随机抽取了100名同学进行身高测量，得到如下频率分布直方图，其中右侧三组小长方形面积成等差数列.则下列说法正确的是（ ）四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题 (2)四川省泸州市2021-2022学年高三第一次教学质量诊断性考试数学（文）试题 (2)三、填空题四、解答题A ．身高在范围内的频率为0.18B ．身高的众数的估计值为115C ．身高的中位数的估计值为125D ．身高的平均数的估计值为121.810.已知正方体的棱长为2，棱AB 的中点为M ，点N 在正方体的内部及其表面运动，使得平面，则（）A．三棱锥的体积为定值B ．当最大时，MN 与BC所成的角为C ．正方体的每个面与点N 的轨迹所在平面夹角都相等D ．若，则点N的轨迹长度为11. 下列说法正确的是（ ）A ．角终边在第二象限或第四象限的充要条件是B．圆的一条弦长等于半径，则这条弦所对的圆心角等于C ．经过小时，时针转了D ．若角和角的终边关于对称，则有12.已知的展开式中共有7项，则（ ）A ．所有项的二项式系数和为64B ．所有项的系数和为1C ．二项式系数最大的项为第4项D ．有理项共4项13. 据某校环保小组调查，某区垃圾量的年增长率为b ，2003年产生的垃圾量为a 吨．由此预测，该区下一年的垃圾量为__________吨，2008年的垃圾量为____________吨．14. 已知定义在上的函数满足，且，若关于的方程有且只有一个实根，则的取值范围是__________．15. 已知公差不为0的等差数列中，存在，，满足，，则项数__________.16. 第五代移动通信技术（5th Generation Mobile Communication Technology，简称5G）是具有高速率、低时延和大连接特点的新一代宽带移动通信技术，5G通讯设施是实现人机物互联的网络基础设施。

泸州市高2021级第一次教学质量诊断性考试数学（文科）本试卷分第1卷（选择题）和第II 卷（非选择题）两部分．第1卷1至2页，第II 卷3至4页．共150分．考试时间120分钟．注意事项：1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．2.选择题的作答1每小题选出答案后，用2B铅笔把答题卡上对应题的答案标号涂黑．3.填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内，作图题可先用铅笔绘出，确认后再用0.5毫米黑色签字笔描清楚，写在试题卷、草稿纸和答题卡上的非答题区域均无效4.考试结束后，请将本试题卷和答题卡一并上交．第1卷（选择题共60分）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．I 已知集合A=｛XII斗<4,xE z}, B=｛斗2x>l}，则AnB=A.{0,1,2,3}B.{1,2,3}C.{2,3}D.{1,3}2.已知命题p :VxER,3">2·`．；命题q :3x 。

ER,lnx 。

=－2,则下列命题是真命题的为A .(-,p )＾qB.p/\q C .p A(-.q)2五3若sinx ＝一—-，则cos2x =1 1 7A.-B.--C .-99 9 4.已知某几何体的三视图如图所示，则该几何体的体积为D .(-,p )＾（-,q )D.－一门一�丿勹上1T俯筏Ill艺2A 竺2BC.2兀 D.4冗5.“碳中和“是指企业、团体或个人通过植树造林、节能减排等形式，抵消自身产生的二氧化碳排放量，实现二氧化碳零排放＇．某地区二氧化碳的排放量S （亿吨）与时间t （年）满足函数关系式S=ab'，已知经过43a年，该地区二氧化碳的排放量为—-（亿吨）．若该地区通过植树造林、节能减排等形式抵消自身产生的二颌4 化碳排放量为己（亿吨），则该地区要实现“碳中和“，至少需要经过（参考数据：lg2""0.30, lg3"" 0.48)3 A.13年B.14年C.15年D.16年6."sin(a-/J)=O “是“tana= tan/J"的A.充分不必要条件C.充要条件B.必要不充分条件D.既不充分也不必要条件7.函数.f (x)2x-1=-—• si11.,"t '的图象大致为2'+1yyyy工A. B. C. D.8.如图，在四棱锥P-ABCD中，底面ABCD为正方形，PA..l底面ABCD,PA=AB, E为线段PB的中点，F 为线段BC 上的动点，则下列结论一定正确的是pcA.平面AEF上平面PBC C.直线EF II平面PCDB.平面AEF上平面ABCD D.直线EF J_平面PAB9 已知f(x)是定义在R 上的奇函数，且满足f(x+2)=f(-x)，当xE(O,I)时，/(x)=ln(x+l)，则f（罕）＝l 一2nA3一2nB2一31 Ic D.ln210.已知菱形ABCD 的边长为6,乙BAD =60•,将t:::,.BCD 沿对角线BD 翻折，使点C 到点P 处，且二面角A -BD -P 为90·,则此时三棱锥P -ABD 的外接球的表面积为A.48冗B.32✓3冗C.20平冗D.60冗11.已知f(x)＝｛釭－l，（x<a)(x-2)2,(x a) 的值域为R，则a的最小值为5A.0B.2C..:...D.I12 已知函数f(x) = 2sin((JJx-f)c{i)>O)在（咚）上存在砓值且在（气，叶上单1问则Q的取值范围是A.［峙］B.［飞］c.[%,甘D.［琵］第I1卷（非选择题共90分）注意事项：(1)非选择题的答案必须用0.5毫米黑色签字笔直接答在答题卡上，作图题可先用铅笔绘出，确认后再用0.5毫米黑色签字笔描清楚，答在试题卷和草稿纸上无效．(2)本部分共10个小题，共90分．二、填空题（本大题共4小题，每小题5分，共20分．把答案填在答题纸上）．13.函数f(x)＝-江的对称中心为x-114.已知一个圆锥的体积为3开，侧面积是底面积的2倍，则其底面半径为15.写出“使函数f(x)= ae x -lnx在区间(1,2)上单调递增＂的实数a的一个值．16.过点(O,m)有两条直线与曲线y=.!.+ lnx相切，则实数m的取值范围是三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17.（本小题满分12分）已知函数f(x) = 2sin2x + 2✓3s i几xcosx-1(I)求函数f(x)的最小正周期；(II)将函数f(x)图象向右平移工个单位长度得到g(x)的图象，若g g十工＝－3，OE O卫，求sin0(2l2) 7 (』的值18.（本小题满分12分）已知x=－是函数／（x)= x2 -1 lx + a lnx的极值点．（I)求a的值(TI)若函数.f(x)在(l,c)上存在最小值，求c 的取值范围19.（本小题满分l2分）心ABC 的内角A,B, C 的对边分别为a,b, c,设12b s inB=c s inAco s B+a s inBco sC.a(I)求一的值；b (II)若a=6,AD为t:::,.ABC 的内角平分线，且AD=CD,求co sC 的值．20.（本小题满分12分）如图，四棱锥P-ABCD 的底面ABCD 是正方形，且平面PBC..L 平面ABCD.0, E 分别是BC,PA 的中点，经过0,D, E 兰点的平面与棱P B 交于点F,平面PB Cn 平面P A D =l ,直线D E 与直线l 交于点G.PF(I)求一一的低PB(II)若PB=PC=CD=2,求多面体POCDEF 的体积．21.（本小题满分12分）已知函数f (x) = tanx-ax.(I)若a I,证明：当XE （吁）时，f(x)>O,(II)若函数g (x) =f (x) + sinx 在（二琴）上有三个零点，求实数a 的取值范围2 2（二）选考题：共IO 分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．22.（本小题满分10分）选修4-4:坐标系与参数方程在直角坐标系xOy中，以坐标原点0为极点，x轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为psin （三］早曲线c 2｛芦：aosa(a为参数）．(I)求C 2的极坐标方程：(II)已知点M(2,0)，曲线C J 的极坐标方程为0=互,C 3与G 的交点为P,与c 2的交点为o,Q,求3 凶PQ的面积．23.（本小题满分10分）选修4-5:不等式选讲已知函数f(x)=lxl+lx-21-1 (I)求不等式f(x)5的解集；a 2(II)若函数f(x)的最小值为m,且a+b=m(a >0,b >0) 求证：——+——-b2Ia+I b+l 3泸州市高2021级第一次教学质量诊断性考试数学（文科）参考答案及评分意见评分说明：I.本解答给出了一种成几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则，2.对计邻题，当考生的解答在某一步出现错误时，如呆后维部分的解答未改变该题的内容和难度可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严堡的错误，就不再给分．3.解答右侧所注分数，表示考生正确做到这一步应得的只加分数，4,只给整数分数，选择题和填空题不给中间分．一、选择题，| :; | ; | ： I ; | ； | ; | ； | ； | ：I : I :二、填空题，11-D 12-C13.(1,1);三、解答题，17,烧由题意，f(x )=-cos 2x ．十石s i n 2-.:...........................................................I 分..fi .~ I =2（一sin 2'<--;:-cos 2x)...............,.............,..........................................2分2 214..[j ;I15.“>－的任意一个实数值；e16.(In 2，如）．冗=2sin (2x-一），．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．.....4分62兀所以函数J (x ）的嵌小正周期T=一－＝冗： (2)6分冗冗冗(II）由聪意，g(:c)= 2si n [2(x －一）－一＝2si n(2x －一）＝一2co s2x,..................….7分66 2°”“因为g(-＋一）＝－2c os (0＋一）＝－一，22 l2 67 冗所以co s(0+－）＝-，I....................................................,..........,............ g 分6 7冗冗冗2冗因为0e(O 一），所以0+－e（一，一），2 6 6 3冗所以sin(B＋一）＝一一，颂........................................................................... 9分6'7冗冗冗冗”“s i n0 = sin[(B＋一）－一＝sin(B ＋一）co s-－c心（0+一）s in一..........……......,......J O 分6 6 6 6 6 6 4✓3 ✓3 1.. 1 11 -—X -－ －一X 一＝－....................................................................... 12分7 2 7 2 14愤j三·文数答案第1页共6页18.解：（I)因为／（x)=x2-llx+alnx,所以/'(x)=2x-l l+f!.(x>O),············.. ·························... ·............. 2分X3因为x=－是函数函数f(x)的极值点，22a所以!'(2)=3-11＋一＝o,3............................................................ 3分(x-4)(2:飞一3)a=12,此时f'(x)•�(x > 0),X......................................... 4分3 3所以f(x)在(0．一）上单调递增，在(-,)上单涸递减，在(4..l.OO）上单调递增，2 2故所求o的值为121．．．．．．．．．．．．．．．．．．．．．．．．．．．妇........................................6分3 3(II)当a=12时，f(x)在(0，一）上单调递增，在(-A)上单调递减，在(4,-t«>）上单调递2 2增，/(1)=1-11=-IO,······························.. ··............................... 7分/(4) =16-44+121n4 =-28+241n 2, ·······•············· ·········......... ··· ······ 8分/(I)-/(4)= -10-(-28-24ln 2)=6(3-lnl6), ·· ··············· ··"....... •·· ····· 10分因为e1>16,所以f(l)> /(4), ·· ···· ·· ·· ··· · ··· ··· ····· ······ ······ ·· ··..... ···· ··11分所以c的取值范围是（4,心))............................... ... . (2)19．衅（l)因为1泌sinB= csinAcosB+asinBcos C.由正弦定理得12sm2B = s inCsi n Aco s B＋血AsinBco s C,· ···．．．．．．．,.......…··2分所以12sm2B=smAsit1(B+C)=sit1Asin[冗一(B+C))=s m2A, ·······……………4分所以12sia12B = sir12 A, ........................................................................... 5分因为A,Be(O，冗），所以sinA >0, sinB>O,所以sin2 A=12si n2 B即2＝史-4=2石b sinB....................................................... 6分（日）解法一：由a=6,a-＝ 2石，得b＝./3'...........................................................7分b设DD=x,则AD=CD=6－．飞，因为AD为/::.ABC的内角平分线，1s .:.AD•ABsin乙BAD 所以土巫＝24空s I CD't:.ACD .:..A D· AC sin L.CAD2AB�D C ................................................ g分所以AB BDAC CD ， AB=石．｀．6-x................................,,,,,.......................... 9分在f:::.ABC中，石飞－（生．）2由余弦定理得co s C= �2x..[3x6设A C的中点为E，连接DE,则DEJ.AC,高三·文数答案第2页共6页 0五CE _ 2在R IA CED 中，co sC =－-=-—·CD 6-x 乱62一（亟)2fJ 所以6-x 2 9 ＝－一，鲜得x=－,2x./3x66-x · "".. ·· 2 §所以co s c =..::t.-=五，．，，．．．．．．，．．．．．．．，．．．．．．．．．．．．．．．．．．．．．．．．．．．，．．．．．．，．．．．．．．..12分6-."C 3解法二：因为AD为!:':.ABC的内角平分线，·,.. ·............. ·.. ·.. ·.... ·...... · · 11分I s .:.,JD • AB s in乙B AD 所以今坐＝2 s I心co .:.AD ·AC sin 乙C A DBDCD ' ................................................ 7分所以AB BD， AC CD记AB BD －一＝一＝1，1,AC CD 由a=6,岊＝2石，得b=石．．．．．．．．．．．．．．．．．．...........................................g 分6 CD=—,L+m 在!:,.ABC中，由余弦定理得cosC = �, 战）2+62一（石m)22x./3x6设AC 的中点为E,连接D E,则DE l AC ,cosC= CE./J(l +m)=,CD 12贝l j AD=..{3m , 6mBD=—, 1+111在Rt6CED中，........................ 9分 0故石项－（岛）2=五�.解得m =3,….........……..................II 分2x$x612 叔l+m)_.fi 所以cosC =＝一－．..............................................................12分123 20.烧（I)因为ADIi BC, AD ,:;:平面PBC,所以从）／／平面PBC,·············..................... J 分因为平面P BCn 平面P AD=l,所以I II AD,............................................. 2分因为直线DE与宜线I 交千点G,连接OG,OG与PB 的交点即为点F ,················........................ 3分因为底而ABCD是正方形，0是BC的中点．AD =20B ,···············... ·.. ·.......................... 4分因为E是PA的中点，可得P G=AD，则PG=20B,因为I ll AD,所以l II BC , l::,PGF "'!::,BOP ,……......……….....…......…5分PF PG PF 所以一－＝－－ ＝2.即一－＝2:............................................................ 6分FB OB . FBOE,多面体POCDEF的休积V=v 区尤{)+V,-,oo +V s －应，…….........7分c（日）连接OP,高三·文数答案第3页共6页因为PB=PC=2,0为BC中点，所以PO」./JC，PO=.JPC2-oc2＝石·又平面PBC上平面A!J C D ，平面PBCn平面AJJC D =BC,POc平面PBC,所以PO J_平面A B CD ,······....................................................................... g分而ODc平面ABCD,所以PO上OD,I I I J 所以Vp.OC D =－x S AOCD x PO =－X-xl x 2x 石＝一·3 3 2 3 ...............,...,....................9分因为E为PA中点，I I所以V8-t”=5V 小沁产了肛。