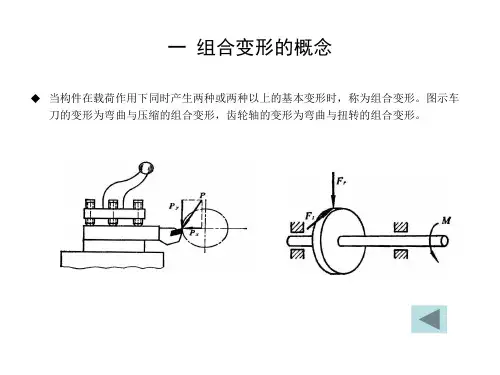
组合变形及强度理论
- 格式:doc
- 大小:274.50 KB
- 文档页数:5








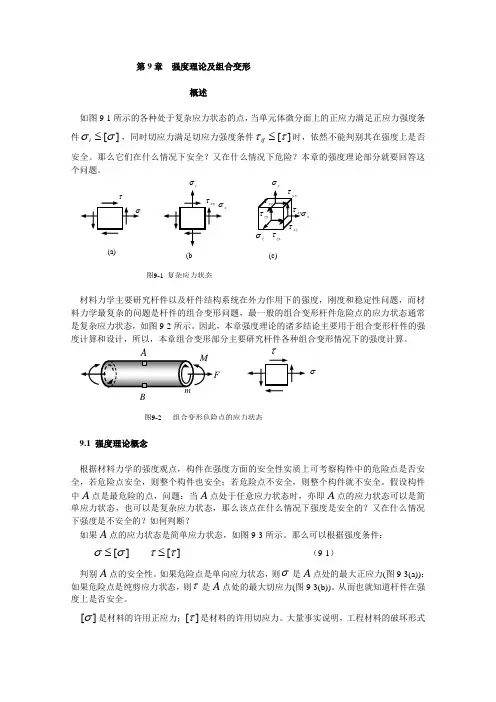
第9章 强度理论及组合变形概述如图9-1所示的各种处于复杂应力状态的点,当单元体微分面上的正应力满足正应力强度条件][σσ≤i,同时切应力满足切应力强度条件][ττ≤ij 时,依然不能判别其在强度上是否安全。
那么它们在什么情况下安全?又在什么情况下危险?本章的强度理论部分就要回答这个问题。
材料力学主要研究杆件以及杆件结构系统在外力作用下的强度,刚度和稳定性问题,而材料力学最复杂的问题是杆件的组合变形问题,最一般的组合变形杆件危险点的应力状态通常是复杂应力状态,如图9-2所示。
因此,本章强度理论的诸多结论主要用于组合变形杆件的强度计算和设计,所以,本章组合变形部分主要研究杆件各种组合变形情况下的强度计算。
9.1 强度理论概念根据材料力学的强度观点,构件在强度方面的安全性实质上可考察构件中的危险点是否安全,若危险点安全,则整个构件也安全;若危险点不安全,则整个构件就不安全。
假设构件中A 点是最危险的点,问题:当A 点处于任意应力状态时,亦即A 点的应力状态可以是简单应力状态,也可以是复杂应力状态,那么该点在什么情况下强度是安全的?又在什么情况下强度是不安全的?如何判断?如果A 点的应力状态是简单应力状态,如图9-3所示。
那么可以根据强度条件:][σσ≤ ][ττ≤ (9-1)判别A 点的安全性。
如果危险点是单向应力状态,则σ是A 点处的最大正应力(图9-3(a));如果危险点是纯剪应力状态,则τ是A 点处的最大切应力(图9-3(b))。
从而也就知道杆件在强度上是否安全。
][σ是材料的许用正应力;][τ是材料的许用切应力。
大量事实说明,工程材料的破坏形式图9-1 复杂应力状态yσxσz σxy τxzτyxτyz τzxτzy τxσy σxy τστ(a)(b(c)ABFMm图9-2 组合变形危险点的应力状态στ主要有两种,一是脆性断裂,二是塑性屈服,脆性断裂的极限应力为强度极限)(b b τσ,而塑性屈服的极限应力为屈服应力)(s s τσ,考虑到诸多偶然因素的影响(如材料缺陷,加工误差,实际工作环境,载荷非理想化等等),所以通常将极限应力除以一个适当的安全系数1>n ,这样就得到材料的许用正应力][σ和许用切应力][τ。

需要课件请或强度理论(一)强度理论的概念1.材料破坏的两种类型材料破坏型式不仅与材料本身的材质有关,而且与材料所处的应力状态、加载速度温度环境等因素有关。
材料在常温、静载荷下的破坏型式主要有以下两种:脆性断裂材料在无显然的变形下骤然断裂。
塑性屈服(流动) 材料浮上显著的塑性变形而丧失其正常的工作能力。
2.强度理论在复杂应力状态下关于材料破坏缘故的假设,称为强度理论。
研究强度理论的目的,在于利用容易应力状态下的实验结果,来建立材料在复杂应力状态下的强度条件。
(二)四个常用的强度理论四个常用强度理论的强度条件可以统一地写成式中σr称为相当应力,其表达式为最大拉应力理论σr1=σ1(第一强度理论)最大拉应变理论σr2=σ1-ν(σ1+σ2)(第二强度理论)最大剪应力理论σr3=σ1-σ3(第三强度理论)形状改变比能理论(第四强度理论)[σ]为材料的许用应力。
第1 页/共18 页对于工程上常见的一种二向应力状态如图5—9—3所示,其特点是平面内某一方向的正应力为零。
设σy=0,则该点的主应力为代入(5—9-15)式得:第三强度理论(最大剪应力理论)的相当应力为第四强度理论(形状改变比能理论)的相当应力为最大拉应力理论、最大拉应变理论是关于脆性断裂的强度理论;最大剪应力理论、形状改变比能理论是关于塑性屈服的强度理论。
强度理论的选用在三向拉应力作用下,材料均产生脆性断裂,故宜用第一强度理论;而在三向压缩应力状态下,材料均产生屈服破坏,故应采用第三或第四强度理论。
当材料处于二向应力状态作用下时:脆性材料易发生断裂破坏,宜用第一或第二强度理论;塑性材料易发生塑性屈服破坏,宜用第三或第四强度理论。
[例5-9-1] 已知构件上某点的应力单元体如图5-9-4(a),(b)所示(图中应力单位为MPa)。
试求指定斜截面上的应力。
[解] 图示单元体处于平面应力状态。
(1)在图示坐标中代人公式(5-9-1)、(5-9-2)得σα、τσ方向如图中所示。
第八章强度理论与组合变形§8-1 强度理论的概念1.不同材料在同一环境及加载条件下对“破坏”(或称为失效)具有不同的抵抗能力(抗力)。
例1常温、静载条件下,低碳钢的拉伸破坏表现为塑性屈服失效,具有屈服极限σ,s铸铁破坏表现为脆性断裂失效,具有抗拉强度σ。
图9-1a,bb2.同一材料在不同环境及加载条件下也表现出对失效的不同抗力。
例2常温静载条件下,带有环形深切槽的圆柱形低碳钢试件受拉时,不再出现塑性变形,而沿切槽根部发生脆断,切槽导致的应力集中使根部附近出现两向和三向拉伸型应力状态。
图(9-2a,b)例3 常温静载条件下,圆柱形铸铁试件受压时,不再出现脆性断口,而出现塑性变形,此时材料处于压缩型应力状态。
图(9-3a )例4 常温静载条件下,圆柱形大理石试件在轴向压力和围压作用下发生明显的塑性变形,此时材料处于三向压缩应力状态下。
图9-3b3.根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹性失效准则,考虑安全系数后,其强度条件为 []σσ≤ ,根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失效准则,考虑安全系数后,强度条件为 []ττ≤ 。
建立常温静载一般复杂应力状态下的弹性失效准则——强度理论的基本思想是: 1)确认引起材料失效存在共同的力学原因,提出关于这一共同力学原因的假设; 2)根据实验室中标准试件在简单受力情况下的破坏实验(如拉伸),建立起材料在复杂应力状态下共同遵循的弹性失效准则和强度条件。
3)实际上,当前工程上常用的经典强度理论都按脆性断裂和塑性屈服两类失效形式,分别提出共同力学原因的假设。
§8-2四个强度理论1.最大拉应力准则(第一强度理论)基本观点:材料中的最大拉应力到达材料的正断抗力时,即产生脆性断裂。
表达式:u σσ=+max复杂应力状态321σσσ≥≥, 当01>σ, 1m a xσσ=+简单拉伸破坏试验中材料的正断抗力b u σσσ==1,032==σσ 最大拉应力脆断准则: b σσ=1(9-1a)相应的强度条件:[]bb n σσσ=≤1(9-1b)适用范围:虽然只突出 1σ 而未考虑 32,σσ 的影响,它与铸铁,工具钢,工业陶瓷等多数脆性材料的实验结果较符合。
组合变形和强度理论习题及解答
题1.图示,水平放置圆截面直角钢杆(2
ABC
p ?),直径100d mm =,2l m =,1q k N m =,[]MPa 160=σ,试校核该杆的强度。
解:
1)各力向根部简化,根截面A 为危险面 扭矩:212nA M
ql =
,弯矩 23
2
zA M ql =+,剪力2A Q ql = 2) 2348ZA M ql W d s p ==, 3132W d p =,3
116
p W d p =, 扭转剪应力:2
3
810.18n P M ql MPa W d
t p ===,
3) []364.42r MPa s s =
=<,
∴梁安全
题2、 平面曲杆在C 端受到铅重力P 作用。
材料的
[σ]=160MPa 。
若P=5KN ,l =1m ,a=0.6m 。
试根据第四强度理论设计轴AB 的直径d. 解:属于弯扭组合变形
危险面A 处的内力为:
题3、平面曲拐在C 端受到铅垂力P 作用,材料的[σ]=160MPa ,E=2.1⨯10
5
MPa ,。
杆的直径
d=80mm ,l =1.4m ,a=0.6m ,l 1=1.0m 。
若P=5KN (1) 试用第三强度理论校核曲拐的强度。
(2) 求1-1截面顶端处沿45︒方向的正应变。
解:
(1)危险A 上的内力为:5 1.4
7z M kN m =??
B
曲拐安全 (2)1-1截面内力:5,3z M kN m
T kN m =?? 顶点的应力状态
题4. 图示一悬臂滑车架,杆AB 为18 号工字钢,其长度为 2.6l m =。
试求当荷载F =25kN 作用在AB 的中点D 处时,杆内的最大正应力。
设工字钢的自重可略去不计。
B
解:18号工字钢4
3421851030610.,.W m A m --=??
AB 杆系弯庄组合变形。
题5. 砖砌烟囱高30h m =,底截面m m -的外径13d m =,内径22d m =,自重
2000P kN =,受1/q kN m =的风力作用。
试求:
(1)烟囱底截面上的最大正应力;
(2)若烟囱的基础埋深04h m =,基础及填土自重按21000P kN =计算,土壤的许用应力
[]0.3MPa s =圆形基础的直径D 应为多大?
注:计算风力时,可略去烟囱直径的变化,把它看作是等截面的。
解:烟囱底截面上的最大正应力:
题 6. 受拉构件形伏如图,已知截面尺寸为405mm mm ´,承受轴向拉力
12F kN =。
现拉杆开有切口,如不计应力集中影响,当材料的[]100MPa s =时,试确定切口的最大许可深度,并绘出切口截面的应力变化图。
解:
题7. 试确定图示各截面的截面核心边界。
解:① 截面几何 ② 截面核心
213
1400007290182400100
,..设中性轴为边,y z z y AB a mm a i y m a z -==?=-=-=-´=
相应荷载作用点为点1;利用对称性,同样可得荷载作用点2 , 3 , 4 。
因此截面核心为点1 ,
2 ,
3 .
4 组成的正方形,该正方形的对角线长度: 题8. 试确定图示各截面的截面核心边界。
解:① 截面几何 ② 截面核心
设中性轴为AB 边,2y
8.4910, z a m a -=-??,则相应的荷载作用点1的坐标为:
2
3
12
12791000329849100
...y
z i z m a y --´=-=-=+-?= 分别设中性轴与点A B 、 和C 相切,则其截跟以及相应的荷载作用点2 , 3 和4 的坐标分别为:中性轴截距:200115,;,z y
z y a a mm a mm a =??=?相应点坐标:
2323440502430,,,;.,.z y mm z mm y ==?-=
中性轴由点A 的切线绕角点A 转至AB 边和由AB 边绕角B 转至点B 的切线,相应的荷载作用点的轨迹为直线,故分别以直线连接点1 、2 和点1 、3 。
中性轴从点A 的切线沿半圆孤ACB 过渡到B 点的切线(始终与圆周相切),则相应的荷载作用点的轨迹必为一曲线,于是以适应的曲线连接点2 、4 、3 即得该截面的截面核心,如图中阴影区域所示,为一扇形面积。
题9. 曲拐受力如图示,其圆杆部分的直径50d mm =。
试画出表示A 点处应力状态的单元体,求其主应力及最大切应力。
解:A 点所在的横截面上承受弯矩和扭矩作用,其值 它们在点A 分别产生拉应力和切应力,其应力状态如图,其中
注:剪力在A 点的切应力为零。
10. 试校核图示拉杆头部的剪切强度和挤压强度。
已知图中尺寸32,20D mm d mm ==和。
12h mm =,杆的许用切应力[]100MPa t =,许用挤压应力[]240bs MPa s =。
解:33
6
39
b C bs b 50501050106632012105010200101026254
.[][]22安全安全
(32-20)s s s s s F KN
F MPa A dh F MPa A t t p p s s p p -=创====<创?创====<´ 11. 两直径100d mm =的圆轴,由凸缘和螺栓连接,共有8 个螺栓布置在0200D mm =的圆周上 ,如图所示。
已知轴在扭转时的最大切应力为70MPa ,螺栓的许用切应力[]60MPa t =。
试求螺栓所需的直径1d 。
解: 9
636
9
1010701010010
1016
max T T t p p -´==4´´´ 12. 一托架如图所示。
已知外力35F kN =,铆钉的直径20d mm =,铆钉与钢板为搭接。
试求拉最危险的铆钉剪切面上切应力的数值及方向。
解;(l)在F 力作用下,因为每个铆钉直径相等.故每个铆钉上所受的力4
sy F
F =
(2)在3
22510M F -=创
力偶作用下,四个铆钉上所受的力应组成力偶与之平衡。
联解式(l )、(2)得
1
1221213
2
6
3152628754
3273271010420
104
max .()
...sx sy s Mr F KN
r r F
F KN F KN
MPa t p -==-?===
´==´´
13. 平均半径为尺的四分之一圈弧的平面曲杆,在自由端承受水平和铅垂方向的两集中力P ,如图所示,试作曲杆的轴力、扭矩和弯矩图。
解:(1)列内力方程
由截面法,可得任一截面上的内力分量(不考虑剪力)为
(2)轴力、扭矩和弯矩图
M M分别如图所示。
由内力方程,可得袖力、扭矩和弯矩(,)
z g
轴力图扭矩图弯矩图。