材料力学强度理论与组合变形
- 格式:doc
- 大小:1.86 MB
- 文档页数:20

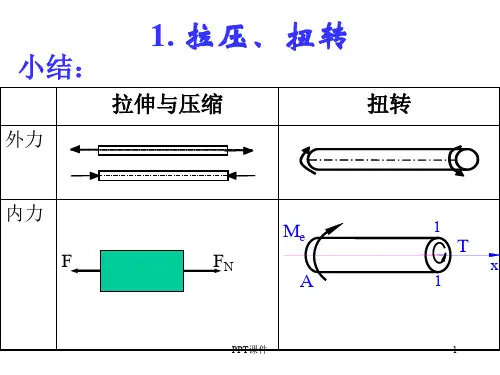



材料力学四大强度理论材料力学是研究材料在外力作用下的力学性能和变形规律的学科,其中强度理论是材料力学中的重要内容之一。
材料的强度是指材料在外力作用下抵抗破坏的能力,而强度理论则是用来描述和预测材料在不同应力状态下的破坏规律和强度值的理论体系。
在材料力学中,有四大经典的强度理论,分别是极限强度理论、绝对最大剪应力理论、莫尔-库伊特理论和最大应变能理论。
首先,极限强度理论是最早被提出的强度理论之一,它是根据材料的屈服条件来描述材料的破坏规律。
极限强度理论认为材料在受到外力作用时,只要应力达到了材料的屈服强度,材料就会发生破坏。
这种理论简单直观,易于应用,但在实际工程中往往存在一定的局限性,因为它忽略了材料在屈服之前的变形过程。
其次,绝对最大剪应力理论是基于材料的最大剪应力来描述材料的破坏规律。
这种理论认为,材料在受到外力作用时,只要材料中的最大剪应力达到了材料的抗剪强度,材料就会发生破坏。
这种理论在一些特定情况下具有较好的适用性,但在一些复杂应力状态下往往难以准确描述材料的破坏规律。
接下来,莫尔-库伊特理论是基于材料的主应力来描述材料的破坏规律。
这种理论认为,材料在受到外力作用时,只要材料中的任意一个主应力达到了材料的抗拉强度或抗压强度,材料就会发生破坏。
莫尔-库伊特理论相对于前两种理论来说,更加全面和准确,因为它考虑了材料在不同应力状态下的破坏规律。
最后,最大应变能理论是基于材料的应变能来描述材料的破坏规律。
这种理论认为,材料在受到外力作用时,只要材料中的应变能达到了材料的抗拉强度或抗压强度,材料就会发生破坏。
最大应变能理论在描述材料的破坏规律时考虑了材料的变形能量,因此在一些复杂应力状态下具有较好的适用性。
综上所述,材料力学中的强度理论是描述和预测材料在外力作用下的破坏规律和强度值的重要理论体系。
四大强度理论分别是极限强度理论、绝对最大剪应力理论、莫尔-库伊特理论和最大应变能理论,它们各自具有一定的适用范围和局限性,工程应用中需要根据具体情况进行选择和应用。
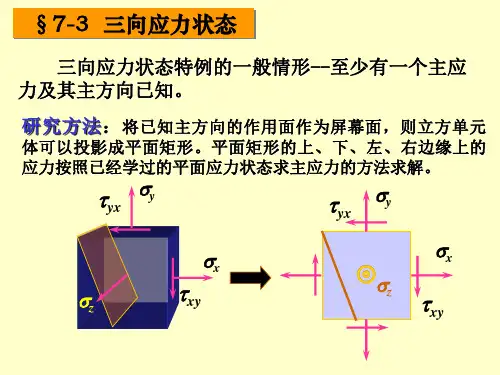

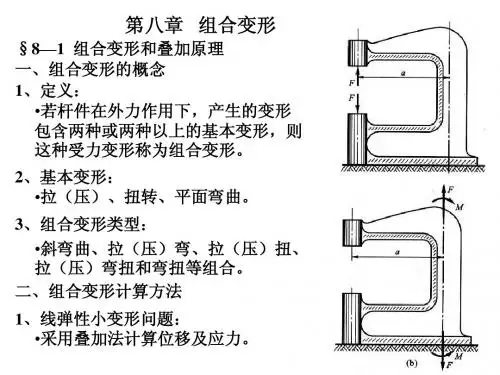

材料力学知识点总结材料力学是研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
它是工程力学的一个重要分支,对于机械、土木、航空航天等工程领域的设计和分析具有重要意义。
以下是对材料力学主要知识点的总结。
一、基本概念1、外力与内力外力是指物体受到的来自外部的作用力,包括集中力、分布力等。
内力则是物体内部各部分之间的相互作用力,当物体受到外力作用时,内力会随之产生以抵抗外力。
2、应力与应变应力是单位面积上的内力,它反映了材料内部受力的强弱程度。
应变是物体在受力作用下形状和尺寸的相对变化,分为线应变和切应变。
3、杆件的基本变形杆件在受力作用下主要有四种基本变形形式:拉伸(压缩)、剪切、扭转和弯曲。
二、拉伸与压缩1、轴力与轴力图轴力是指杆件沿轴线方向的内力。
通过绘制轴力图,可以直观地表示出轴力沿杆件轴线的变化情况。
2、横截面上的应力在拉伸(压缩)情况下,横截面上的应力均匀分布,其大小等于轴力除以横截面面积。
3、材料在拉伸与压缩时的力学性能通过拉伸试验,可以得到材料的强度指标(屈服强度、抗拉强度)和塑性指标(伸长率、断面收缩率)。
不同材料具有不同的力学性能,如低碳钢的屈服和强化阶段,铸铁的脆性等。
4、胡克定律在弹性范围内,应力与应变成正比,即σ =Eε ,其中 E 为弹性模量。
5、拉伸(压缩)时的变形计算根据胡克定律,可以计算杆件在拉伸(压缩)时的变形量。
三、剪切1、剪切内力与剪切应力剪切内力通常用剪力表示,剪切应力则是单位面积上的剪力。
2、剪切实用计算在工程中,通常采用实用计算方法来确定剪切面上的平均应力。
四、扭转1、扭矩与扭矩图扭矩是指杆件在扭转时横截面上的内力偶矩。
扭矩图用于表示扭矩沿杆件轴线的变化。
2、圆轴扭转时的应力与变形圆轴扭转时,横截面上的应力分布呈线性规律,其最大应力发生在圆周处。
扭转角的计算与材料的剪切模量、扭矩和轴的长度等因素有关。
五、弯曲1、剪力与弯矩弯曲内力包括剪力和弯矩,它们的计算和绘制剪力图、弯矩图是弯曲分析的重要内容。


材料力学大四:组合变形(二)(弯.+扭.;拉+扭;压+扭;弯+弯+扭;拉+弯+扭) 题目材大4-1如图1所示传动轴AB 直径=120mm d ,轴长=3.6m L ,[]120MPa σ=,轮缘挂重物=12kN F 与扭转力偶矩e M 平衡,皮带轮C 的直径=800mm D 。
试按第三强度理论校核轴的强度。
图1材大4-1 图2大4-2材大4-2如图2所示钢制圆轴,直径为=100mm d ,若轴上作用的载荷=4.0kN F ,e =2.0kN m M ⋅,圆轴材料的许用应力[]=80MPa σ。
按第三强度理论校核圆轴的强度。
材大4-3一水平放置的直角曲拐如图3所示,在C 端受竖直向下力F 和平行AB 段轴线的力F 作用,AB 段为一直径为d 的等直圆杆, 1.5l a =,10a d =,试推导AB 段危险点的第三强度理论相当应力(用F 和d 表示)。
图3大4-3 图4大4-4材大4-4如图4所示传动结构中等截面圆轴AB 的直径为d ,抗弯截面系数为W ,轮C 、D 的直径均为4d ,两皮带张力分别为F 和3F ,方向分别与y 轴、z 轴平行。
(1)画内力图,指出圆轴AB 危险截面的位置; (2)计算危险点的第四强度理论相当应力。
材大4-5直角曲拐位于水平面内,A 端固定,AB 段为圆截面,自由端C 处受铅垂载荷F 作用。
如图5(a)所示。
由试验测得AB 段中间表面a 点处沿轴向方向线应变40104-⨯=ε,表面点b 处沿与母线成 45方向的线应变445103-⨯-=ε,(b 点在中性层上),如图4(b)所示。
已知材料的弹性模量200=E GPa ,泊松比3.0=ν,许用应力[]160=σMPa 。
试求:(1)画AB 段的内力图确定危险截面; (2)画a 、b 两点应力状态单元体; (3)采用第四强度理论校核AB 段的强度。
(a) (b)图5大4-4材大4-6(习14-6)皮带传动轴由电机带动,尺寸及受力如图6所示,皮带轮重=1kN G ,直径=1200mm D ,T 6kN F =,t =3kN F 。
材料力学知识点总结材料力学是一门研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科,它是工程力学的重要组成部分,对于机械、土木、航空航天等工程领域都有着至关重要的作用。
以下是对材料力学主要知识点的总结。
一、拉伸与压缩拉伸和压缩是材料力学中最基本的受力形式。
在拉伸或压缩时,杆件横截面上的内力称为轴力。
轴力的正负规定为:拉伸时轴力为正,压缩时轴力为负。
通过实验可以得到材料在拉伸和压缩时的应力应变曲线。
低碳钢的拉伸应力应变曲线具有明显的四个阶段:弹性阶段、屈服阶段、强化阶段和局部变形阶段。
弹性阶段内应力与应变成正比,遵循胡克定律;屈服阶段材料出现明显的塑性变形;强化阶段材料抵抗变形的能力增强;局部变形阶段试件在某一局部区域产生显著的收缩,直至断裂。
对于拉伸和压缩杆件,其横截面上的正应力计算公式为:$\sigma =\frac{N}{A}$,其中$N$为轴力,$A$为横截面面积。
而纵向变形量$\Delta L$可以通过公式$\Delta L =\frac{NL}{EA}$计算,其中$E$为材料的弹性模量,$L$为杆件长度。
二、剪切与挤压剪切是指在一对相距很近、大小相等、方向相反的横向外力作用下,杆件的横截面沿外力作用方向发生相对错动的变形。
在剪切面上的内力称为剪力。
剪切面上的平均切应力计算公式为:$\tau =\frac{Q}{A}$,其中$Q$为剪力,$A$为剪切面面积。
挤压是在连接件与被连接件之间,在接触面上相互压紧而产生的局部受压现象。
挤压面上的应力称为挤压应力,其计算公式为:$\sigma_{jy} =\frac{F_{jy}}{A_{jy}}$,其中$F_{jy}$为挤压力,$A_{jy}$为挤压面面积。
三、扭转扭转是指杆件受到一对大小相等、方向相反且作用面垂直于杆件轴线的力偶作用时,杆件的横截面将绕轴线产生相对转动。
圆轴扭转时,横截面上的内力是扭矩。
扭矩的正负规定:右手螺旋法则,拇指指向截面外法线方向为正,反之为负。
第八章 强度理论与组合变形 §8-1 强度理论的概念
1.不同材料在同一环境及加载条件下对“破坏”(或称为失效)具有不同的抵抗能力(抗力)。 例1 常温、静载条件下,低碳钢的拉伸破坏表现为塑性屈服失效,具有屈服极限s,铸铁破坏表现为脆性断裂失效,具有抗拉强度 b。图9-1a,b
2.同一材料在不同环境及加载条件下也表现出对失效的不同抗力。 例2 常温静载条件下,带有环形深切槽的圆柱形低碳钢试件受拉时,不再出现塑性变形,而沿切槽根部发生脆断,切槽导致的应力集中使根部附近出现两向和三向拉伸型应力状态。图(9-2a,b) 例3 常温静载条件下,圆柱形铸铁试件受压时,不再出现脆性断口,而出现塑性变形,此时材料处于压缩型应力状态。图(9-3a)
例4 常温静载条件下,圆柱形大理石试件在轴向压力和围压作用下发生明显的塑性变形,此时材料处于三向压缩应力状态下。图9-3b 3.根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹性失效准则,考虑安全系数后,其强度条件为 ,根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失效准则,考虑安全系数后,强度条件为 。 建立常温静载一般复杂应力状态下的弹性失效准则——强度理论的基本思想是: 1)确认引起材料失效存在共同的力学原因,提出关于这一共同力学原因的假设; 2)根据实验室中标准试件在简单受力情况下的破坏实验(如拉伸),建立起材料在复杂应力状态下共同遵循的弹性失效准则和强度条件。 3)实际上,当前工程上常用的经典强度理论都按脆性断裂和塑性屈服两类失效形式,分别提出共同力学原因的假设。
§8-2四个强度理论 1.最大拉应力准则(第一强度理论) 基本观点:材料中的最大拉应力到达材料的正断抗力时,即产生脆性断裂。 表达式:umax 复杂应力状态 321, 当01, 1max
简单拉伸破坏试验中材料的正断抗力
bu1,032
最大拉应力脆断准则: b1 (9-1a) 相应的强度条件: bbn1 (9-1b) 适用范围:虽然只突出 1 而未考虑 32, 的影响,它与铸铁,工具钢,工业陶瓷等多数脆性材料的实验结果较符合。特别适用于拉伸型应力状态(如0321),混合型应力状态中拉应力占优者( ,0,031但31 )。 2.最大伸长线应变准则(第二强度理论)
基本观点:材料中最大伸长线应变到达材料的脆断伸长线应变 u时,即产生脆性断裂。 表达式:
umax 复杂应力状态
321
,当01,
)(13211max
E
简单拉伸破坏试验中材料的脆断伸长线应变
b1,032,Ebbu
最大伸长线应变准则: b)(321 (9-2a) 相应的强度条件: bbn)(321 (9-2b) 适用范围:虽然考虑了2,3的影响,它只与石料、混凝土等少数脆性材料的实验结果较符合(如图9-4所示),铸铁在混合型压应力占优应力状态下(01313,0,)的实验结果也较符合,但上述材料的脆断实验不支持本理论描写的2,3
对材料强度的影响规律。 3.最大剪应力准则(第三强度理论)
基本观点:材料中的最大剪应力到达该材料的剪切抗力u时,即产生塑性屈服。 表达式:umax 复杂应力状态
简单拉伸屈服试验中的剪切抗力
s1 ,032,2ssu
最大剪应力屈服准则: s31 (9-3a) 相应的强度条件: ssn31 (9-3b)321
,
23113maax 适用范围:虽然只考虑了最大主剪应力 13 ,而未考虑其它两个主剪应力 12 ,32 的影响,但与低碳钢、铜、软铝等塑性较好材料的屈服试验结果符合较好;并可用于像硬铝那样塑性变形较小,无颈缩材料的剪切破坏,此准则也称特雷斯卡(Tresca)屈服准则。
3.形状改变比能准则(第四强度理论) 基本观点:材料中形状改变比能到达该材料的临界值 ufu)( 时,即产生塑性屈服。 表达式:uffuu)( 复杂应力状态
321
,
2132322
21)()()(61Evuf
简单拉伸屈服试验中的相应临界值
s1,032,
2261)(sufEvu
形状改变比能准则: s213232221)()()(21 (9-4a) 相应的强度条件: ssn213232221)()()(21 (9-4b) 适用范围:它既突出了最大主剪应力对塑性屈服的作用,又适当考虑了其它两个主剪应力的影响,它与塑性较好材料的试验结果比第三强度理论符合得更好。此准则也称为米泽斯(Mises )屈服准则,由于机械、动力行业遇到的载荷往往较不稳定,因而较多地采用偏于安全的第三强度理论;土建行业的载荷往往较为稳定,因而较多地采用第四强度理论。 *附:泰勒——奎尼(Taylor—Quinney)薄壁圆筒屈服试验(1931)。 米泽斯与特雷斯卡屈服准则的试验验证。 薄壁圆筒承受拉伸与扭转组合作用时,应力状态如图9-5a。 主应力:223,14212 ,02
代入第三强度理论:2224s 或 1422ss (a) 代入第四强度理论:2223s 或 1322ss (b) (a),(b)式在以s—s为坐标轴的平面内为两条具有不同短轴的理论椭圆曲线(图9-5b)。 结果:试验点基本上落于两条理论曲线之间,大多数试验点更接近于第四强度理论曲线。 莫尔强度理论 1.不同于四个经典强度理论,莫尔理论不致力于寻找(假设)引起材料失效的共同力学原因,而致力于尽可能地多占有不同应力状态下材料失效的试验资料,用宏观唯象的处理方法力图建立对该材料普遍适用(不同应力状态)的失效条件。 2.自相似应力圆与材料的极限包络线 自相似应力圆:如果一点应力状态中所有应力分量随各个外载荷增加成同一比例同步增
加,则表现为最大应力圆自相似地扩大。 材料的极限包络线:随着外载荷成比例增加,应力圆自相似地扩大,到达该材料出现塑性屈服或脆性断裂时的极限应力圆。只要试验技术许可,务求得到尽可能多的对应不同应力状态的极限应力圆,这些应力圆的包络线即该材料的极限(状态)包络线。图9-6a所示即包含拉伸、圆轴扭转、压缩三种应力状态的极限包络线。
3.对拉伸与压缩极限应力圆所作的公切线是相应材料实际包络线的良好近似(图9-6b)。实际载荷作用下的应力圆落在此公切线之内,则材料不会失效,到达此公切线即失效。由图示几何关系可推得莫尔强度失效准则。
对于抗压屈服极限sc大于抗拉屈服极限s的材料(即ssc)
sscs31 (9-5a)
对于抗压强度极限bc大于抗拉强度极限b的材料(即bbc) bbcb31 (9-5b) 强度条件具有同一形式: 31k
或 31ct (9-5c)
相应于式(9-5a),scsk,ssn; 相应于式(9-5b),bcbk, bbn 对铸铁 4.0~2.0k ,陶瓷材料 2.0~1.0k ,对大多数金属,ssc ,此时莫尔强度条件退化为最大剪应力强度条件。 4.适用范围:
1)适用于从拉伸型到压缩型应力状态的广阔范围,可以描述从脆性断裂向塑性屈服失效形式过渡(或反之)的多种失效形态,例如“脆性材料”在压缩型或压应力占优的混合型应力状态下呈剪切破坏的失效形式。 2)特别适用于抗拉与抗压强度不等的材料。 3)在新材料(如新型复合材料)不断涌现的今天,莫尔理论从宏观角度归纳大量失效数据与资料的唯象处理方法仍具有广阔应用前景。
§11-1 组合变形的概念 1.构件的受力情况分为基本受力(或基本变形)形式(如中心受拉或受压,扭转,平面弯曲,剪切)和组合受力(或组合变形)形式。组合变形由两种以上基本变形形式组成。 2.处理组合变形构件的内力、应力和变形(位移)问题时,可以运用基于叠加原理的叠加法。 叠加原理:如果内力、应力、变形等与外力成线性关系,则在小变形条件下,复杂受力情况下组合变形构件的内力,应力,变形等力学响应可以分成几个基本变形单独受力情况下相应力学响应的叠加,且与各单独受力的加载次序无关。
说明: ①保证上述线性关系的条件是线弹性材料,加载在弹性范围内,即服从胡克定律; ②必须是小变形,保证能按构件初始形状或尺寸进行分解与叠加计算,且能保证与加载次序无关。如10-1a图所示纵横弯曲问题,横截面上内力(图10-1b)为N=P,
M(x)=)(222xpxqxql。可见当挠度(变形)较大时,弯矩中与挠度有关的附加弯矩不能略去。虽然梁是线弹性的,弯矩、挠度与P的关系却仍为非线性的,因而不能用叠加法。除非梁的刚度较大,挠度很小,轴力引起的附加弯矩可略去。