北京市中国人民大学附属中学2016-2017学年高一下学期期末考试数学附加题试题+Word版含解析
- 格式:pdf
- 大小:54.65 KB
- 文档页数:3

丰台区2016—2017学年度第二学期期末练习高一数学第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 如果,那么下列不等式中一定成立的是A. B. C. D.【答案】A【解析】由不等式的性质,如果,则.本题选择A选项.2. 等比数列中,,,则A. B. 4 C. D. 8【答案】B【解析】由等比数列的性质可知,成等比数列,则: .本题选择B选项.3. 执行如图所示的程序框图,如果输入的,则输出的等于A. 2B. 4C. 6D. 8【答案】B【解析】流程图等价于分段函数:,则: .本题选择B选项.点睛:在画程序框图时首先要进行结构的选择.若所要解决的问题不需要分情况讨论,只用顺序结构就能解决;若所要解决的问题要分若干种情况讨论时,就必须引入条件结构;若所要解决的问题要进行许多重复的步骤,且这些步骤之间又有相同的规律时,就必须引入变量,应用循环结构.4. 某几何体的三视图如图所示,其中俯视图是等腰三角形,那么该几何体的体积是A. 96B. 128C. 140D. 152【答案】A【解析】由三视图可知,该几何体是一个三棱柱,底面积为等腰三角形,其中底为6,底边上的高为4,三棱柱的高为8,该几何体的体积为: .本题选择A选项.5. 在△中,角,,的对边分别为,,,且,,则△一定是...A. 直角三角形B. 钝角三角形C. 等边三角形D. 等腰直角三角形【答案】C【解析】由余弦定理可得:b2=a2+c2−2accosB=a2+c2−ac=ac,化为(a−c)2=0,解得a=c.又B=60°,可得△ABC是等边三角形,本题选择C选项.6. 二次函数的部分对应值如下表:则一元二次不等式的解集是A. B.C. D. ...【答案】C【解析】由题意可知:一元二次方程ax2+bx+c=0的两个实数根为−2,3(a<0),则ax2+bx+c>0解为−2<x<3,故不等式的解集为{x|−2<x<3},本题选择C选项.点睛:“三个二次”间关系,其实质是抓住二次函数y=ax2+bx+c(a≠0)的图象与横轴的交点、二次不等式ax2+bx+c>0(a≠0)的解集的端点值、二次方程ax2+bx+c=0(a≠0)的根是同一个问题.解决与之相关的问题时,可利用函数与方程思想、化归思想将问题转化,结合二次函数的图象来解决.7. 在数列中,,且,则A. B. C. D.【答案】A【解析】由题意可得,数列是首项为,公差的等差数列,则通项公式:,且:,据此可得:本题选择A选项.点睛:使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源与目的.8. 已知各项均为正数的等比数列中,如果,那么这个数列前3项的和的取值X 围是A. B. C. D.【答案】D【解析】设等比数列的公比为,则:,当且仅当时等号成立,即这个数列前3项的和的取值X围是.9. 已知n次多项式,在求值的时候,不同的算法需要进行的运算次数是不同的.例如计算(k=2,3,4,…,n)的值需要k-1次乘法运算,按这种算法进行计算的值共需要9次运算(6次乘法运算,3次加法运算).现按右图所示的框图进行运算,计算的值共需要次运算.A.B.C.D.【答案】B【解析】阅读流程图可得,该流程图表示的是秦九韶算法,由秦九韶算法的特征结合所给多项式的特点可得计算的值共需要2n次运算,其中加法、乘法运算各n次.本题选择B选项.10. 如图,在正方体中,点在正方体表面运动,如果,那么这样的点共有...A. 2个B. 4个C. 6个D. 无数个【答案】C【解析】设点A到直线的距离为,则满足题意的点位于以为轴,以位半径的圆柱上,即满足题意的点为圆柱与正方体的交点,由几何关系可得,交点的个数为个.本题选择C选项.第二部分(非选择题共60分)二、填空题共6小题,每小题4分,共24分.11. 从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:质量指标值分组[75,85) [85,95)[95,105)[105,115)[115,125]频数 6 26 38 22 8则样本的该项质量指标值落在[105,125]上的频率为_____.【答案】0.3【解析】由频率计算公式可得,样本的该项质量指标值落在[105,125]上的频率为 .12. 函数的最大值是_____.【答案】1...【解析】题中所给的二次函数开口向下,对称轴为,则函数的最大值为: .13. 如图,样本数为的三组数据,它们的平均数都是,频率条形图如下,则标准差最大的一组是_____.【答案】第三组【解析】由题意,标准差越大,数据的波动越大,观察题中所给数据,第一组和第二组均没有波动,则标准差最大的一组是第三组.点睛:D(X)表示随机变量X对E(X)的平均偏离程度,D(X)越大表明平均偏离程度越大,说明X的取值越分散,反之,D(X)越小,X的取值越集中.14. 已知两条不重合的直线和两个不重合的平面,,给出下列命题:①如果,,那么;②如果,,那么;③如果,,那么;④如果,,那么.上述结论中,正确结论....的序号是_____(写出所有正确结论的序号).【答案】②③【解析】由线面关系逐一考查所给的各个命题:①如果,,那么不一定有,该命题错误;②如果,,那么,该命题正确;③如果,,那么,该命题正确;④如果,,那么不一定有,该命题错误.综上,正确的结论为②③ .15. 如图,为了测量河对岸两点之间的距离.观察者找到了一个点,从可以观察到点;找到了一个点,从可以观察到点;找到了一个点,从可以观察到点.并测量得到图中一些数据,其中,,,,,,则_____.【答案】【解析】由特殊三角形的特征可得:,在△ABC中应用余弦定理:.16. 数列满足,,其前项和为,则(1)_______;(2)_______.【答案】 (1). 4 (2).【解析】由递推关系可得:,两式做比值可得:,则:,由可得:,...则奇数项、偶数项分别为首项为1,公比为2的等比数列,则:点睛:数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,由递推关系求数列的通项公式,常用的方法有:①求出数列的前几项,再归纳猜想出数列的一个通项公式;②将已知递推关系式整理、变形,变成等差、等比数列,或用累加法、累乘法、迭代法求通项.三、解答题共4小题,共36分.解答应写出文字说明,演算步骤或证明过程.17. 在△中,角,,的对边分别为,,,且,.(Ⅰ)求的值;(Ⅱ)如果,求的值及△的面积.【答案】(Ⅰ); (Ⅱ).【解析】试题分析:(1)由正弦定理结合题意可得;(2)由余弦定理结合三角形的面积公式可得.试题解析:(Ⅰ)因为以及,所以,因为所以(Ⅱ)因为以及所以,因为,所以因为,,所以所以.18. 某校在“普及环保知识节”后,为了进一步增强环保意识,从本校学生中随机抽取了一批学生参加环保基础知识测试.经统计,这批学生测试的分数全部介于75至100之间.将数据分成以下组:第1组,第2组,第3组,第4组,第5组,得到如图所示的频率分布直方图.(Ⅰ)求a的值;(Ⅱ)现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生座谈,求每组抽取的学生人数;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计随机抽取学生所得测试分数的平均值在第几组(只需写出结论).【答案】(1);(2)从,,组应依次抽取名学生,名学生,名学生;(3) 第3组.【解析】试题分析:(1)由小长方形面积和为1列方程可得;(2)由分层抽样比可得从,,组应依次抽取名学生,名学生,名学生;...(3)由频率分布直方图计算平均值的特点结合中点值的特征可得随机抽取学生所得测试分数的平均值在第三组.试题解析:(1)因为各组的频率之和为1,,解得(2)由频率分布直方图知,第,,组的学生人数之比为.所以,每组抽取的人数分别为:第组:;第组:;第组:.所以从,,组应依次抽取名学生,名学生,名学生.(3)第3组点睛:一是在频率分布直方图中,小矩形的高表示频率/组距,而不是频率;二是利用频率分布直方图求众数、中位数和平均数时,应注意三点:①最高的小长方形底边中点的横坐标即是众数;②中位数左边和右边的小长方形的面积和是相等的;③平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.19. 如图,在四棱锥中,底面为正方形,点是棱的中点,,平面平面.(Ⅰ)求证://平面;(Ⅱ)求证:平面;(Ⅲ) 设,试判断平面⊥平面能否成立;若成立,写出的一个值(只需写出结论).【答案】(Ⅰ)见解析; (Ⅱ)见解析(Ⅲ) 不能成立.【解析】试题分析:(1)由题意可得EO// PC,利用线面平行的判定定理可得PC//平面BDE;(2)利用题意证得PC⊥AC,PC⊥BD,结合线面垂直的判定定理即可证得结论;(3)由空间关系可知面面垂直的关系不能成立.试题解析:证明:(Ⅰ)证明:设,连接,因为底面为正方形,所以是的中点,又点是棱的中点,所以EO是的中位线,所以EO// PC因为EO平面,平面,所以PC//平面BDE;(Ⅱ)证明:(法一)在和中,因为,,,所以≌,又点是棱的中点,所以,所以,因为平面平面,平面平面,平面所以平面,所以EO⊥AC,EO⊥BD,因为EO//PC所以PC⊥AC,PC⊥BD,又AC∩BD=O所以PC⊥平面ABCD.(法二)连接PO因为底面ABCD是正方形,所以O是BD的中点,BD⊥AC,又PB=PD,所以PO⊥BD,又PO∩AC=O,PO平面PAC,AC平面PAC所以BD⊥平面PAC又OE平面PAC, 所以BD⊥OE,因为平面平面,平面平面,平面所以平面,所以EO⊥AC,EO⊥BD,因为OE∥PC,所以PC⊥AC,PC⊥BD,又AC∩BD=O所以所以PC⊥平面ABCD.(Ⅲ) 不能成立20. 设数列满足,;数列的前项和为,且.(Ⅰ)求数列和的通项公式;(Ⅱ)把数列和的公共项...从小到大排成新数列,试写出,,并证明为等比数列....【答案】(Ⅰ),; (Ⅱ)见解析.【解析】试题分析:(1)累加求和可得,结合的通项公式可得(2)由(1)的结论可知,,结合题意和(1)中的结果即可证得数列为等比数列. 试题解析:(Ⅰ)由已知,当时,.又因为,所以数列的通项公式为.因为,所以,两式做差可得,且也满足此式,所以.(Ⅱ)由,,可得,.假设,则.所以,不是数列中的项;,是数列中的第项. 所以,从而.所以是首项为,公比为的等比数列.。

北京市西城区2016-2017学年度第二学期期末试卷高一数学参考答案及评分标准2017.7一、选择题:本大题共10小题,每小题4分,共40分.1. A2. B3. B4. B5. D6. A7. C8. D9. C10. C二、填空题:本大题共6小题,每小题5分,共30分.11. [2,2]-; 12.52; 13. 172,45; 14. 73; 15. 59; 16. 4,29.注:一题两空的题目,第一空2分,第二空3分. 三、解答题:本大题共6小题,共80分. 17.(本小题满分13分)(Ⅰ)解:设等差数列{}n a 的公差为d ,则3512616a a a d +=+=, ………………………3分 又因为12a =,解得2d =. ………………………5分 所以1(1)2n a a n d n =+-=. ………………………7分 (Ⅱ)解:因为2a ,m a ,2m a 成等比数列,所以222m m a a a =⋅, ………………………10分即2(2)44m m =⨯,m *∈N ,解得4m =. ………………………13分18.(本小题满分13分)(Ⅰ)解:因为各组的频率之和为1,所以月均用水量在区间[10,12)的频率为 1(0.02520.0750.1000.225)20.1-⨯+++⨯=,所以,图中实数0.120.050a =÷=. ………………………3分 (Ⅱ)解:由图可知, 样本数据中月均用水量低于8吨的频率为(0.0250.0750.225)20.65++⨯=, ………………………5分所以小明所在学校2000名同学家庭中,月均用水量低于8吨的约有0.6520001300⨯=(户). ………………………7分(Ⅲ)解:设“这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组”为事件A , 由图可知, 样本数据中月均用水量在[10,12)的户数为0.0502404⨯⨯=.记这四名同学家庭分别为,,,a b c d ,月均用水量在[12,14]的户数为0.0252402⨯⨯=.记这两名同学家庭分别为,e f , 则选取的同学家庭的所有可能结果为:(,),(,),(,),(,),(,),(,),(,),a b a c a d a e a f b c b d (,),(,),(,),(,),(,),(,),(,),(,),b e b f c d c e c f d e d f e f 共15种, ………………………9分事件A 的可能结果为:(,),(,),(,),(,),a e a f b e b f (,),(,),(,),(,),c e c f d e d f 共8种, ………………………11分 所以8()15P A =. ………………………13分19.(本小题满分13分)(Ⅰ)解:由余弦定理2222cos c a b ab C =+-, ………………………3分 得2149223()164c =+-⨯⨯⨯-=,解得4c =. ………………………5分(Ⅱ)解:(方法一)由1cos 4C =-,(0,π)C ∈,得sin C ==.……7分由正弦定理sin sin a c A C =,得sin sin a C A c ==. ……………………10分所以cos A ==. 因为πA B C ++=,所以sin sin()B A C =+sin cos cos sin A C A C =+ ………………………12分1()4-+=. ………………………13分(方法二)由1cos 4C =-,(0,π)C ∈,得sin C …………7分 由余弦定理2222cos c a b ab C =+-, 得2124422()4b b =+-⨯⨯⨯-,解得4b =,或5b =-(舍). ………………………10分 由正弦定理sin sin b c B C =,得sin sin b C B c ==………………………13分20.(本小题满分13分)(Ⅰ)解:当1n =时,113a S ==-; ………………………1分 当2n ≥时,125n n n a S S n -=-=-, ………………………3分 因为13a =-符合上式,所以25n a n =-*()n ∈N . ………………………4分 (Ⅱ)解:由(Ⅰ),得2521n n b -=+. ………………………5分 所以12n n T b b b =+++3125(21)(21)(21)n ---=++++++3125(222)n n ---=++++ ………………………6分32(14)14n n --=+-1(41)24n n =-+. ………………………9分(Ⅲ)解:122311111111131335(25)(23)n n a a a a a a n n +=-++++⨯⨯--+++2111111[(1)()()]323352523n n =-+-+-++---11646n =---, ………………………11分 当1n =时,12113a a =,(注:此时1046n <-) 由题意,得13λ≥; ………………………12分当2n ≥时, 因为1046n >-, 所以1223111116n n a a a a a a +<-+++. 因为对于任意正整数n ,都有12231111n n a a a a a a λ++++≤, 所以λ的最小值为13. ………………………13分21.(本小题满分14分)(Ⅰ)解:由2()340f x x x =+-=,解得4x =-,或1x =.所以函数()f x 有零点4-和1. ………………………3分 (Ⅱ)解:(方法1)因为()f x 的图象在直线2y x =+的上方,所以2(21)2ax a x b x +++>+对x ∈R 恒成立.即2220ax ax b ++->对x ∈R 恒成立. ………………………5分所以当0x =时上式也成立,代入得2b >. ………………………8分 (方法2)因为()f x 的图象在直线2y x =+的上方, 所以2(21)2ax a x b x +++>+对x ∈R 恒成立.即2220ax ax b ++->对x ∈R 恒成立. ………………………5分 当0a =时,显然2b >. 当0a ≠时,由题意,得0a >,且2(2)4(2)0a a b ∆=--<, ………………………6分 则24(2)40a b a ->>, 所以4(2)0a b ->,即2b >.综上,2b >. ………………………8分(Ⅲ)解:由题意,得不等式2(21)20ax a x +++<,即(1)(2)0ax x ++<. …………9分当0a =时,不等式化简为20x +<,解得2x <-; ………………………10分当0a ≠时,解方程(1)(2)0ax x ++=,得根12x =-,21x a=-. 所以,当0a <时,不等式的解为:2x <-,或1x a>-; ………………………11分 当102a <<时,不等式的解为:12x a-<<-; ………………………12分 当12a =时,不等式的解集为∅; ………………………13分 当12a >时,不等式的解为:12x a-<<-. ………………………14分综上,当0a <时,不等式的解集为{|2x x <-,或1}x a >-;当0a =时,不等式的解集为{|2}x x <-;当102a <<时,不等式的解集为1{|2}x x a -<<-;当12a =时,不等式的解集为∅;当12a >时,不等式的解集为1{|2}x x a -<<-.22.(本小题满分14分)(Ⅰ)解:36p =,或13. ………………………3分 (Ⅱ)解:由题意,17a =,代入,得212a =,36a =,43a =,58a =,64a =,72a =,81a =,96a =,所以数列{}n a 中的项,从第三项起每隔6项重复一次(注:39a a =), ………5分 故15012348345624()S a a a a a a a a a =+++++++++71224(638421)6384=+++++++++++ 616=.………………………8分(Ⅲ)解:由数列{}n a 的定义,知*n a ∈N .设t 为数列{}n a 中最小的数,即min{}i t a i =∈N *, 又因为当n a 为偶数时,12nn a a +=, 所以t 必为奇数. ………………………9分 设k a t =,则15k a t +=+,252k t a ++=, 所以52t t +≤,解得5t ≤. 所以{1,3,5}t ∈. ………………………10分如果3k a t ==,那么由数列{}n a 的定义,得18k a +=,24k a +=,32k a +=,41k a +=, 这显然与3t =为{}n a 中最小的数矛盾,所以3t ≠. ………………………12分 如果5k a t ==, 当1k =时,5p =;当2k ≥时,由数列{}n a 的定义,得1k a -能被5整除,…,得1a p =被5整除; 所以当且仅当*15()a p r r ==∈N 时,5t =. ………………………13分 这与题意不符.所以当*15()a r r ≠∈N 时,数列{}n a 中最小的数1t =,即符合条件的p 值的集合是*{|r r ∈N ,且r 不能被5整除}. …………………14分。
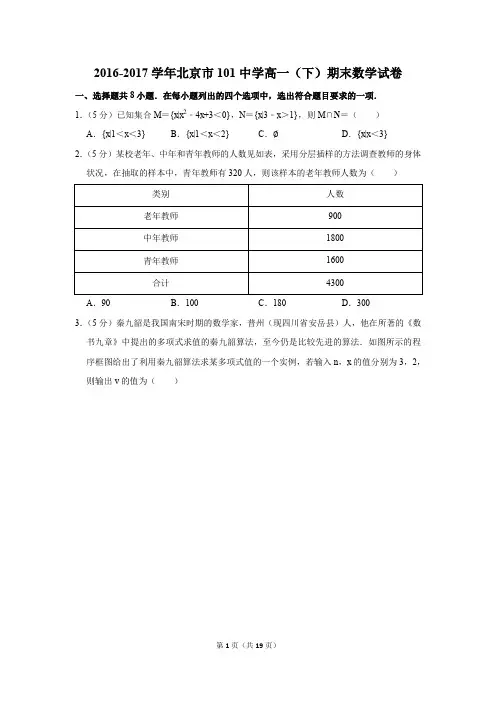
2016-2017学年北京市101中学高一(下)期末数学试卷一、选择题共8小题.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合M={x|x2﹣4x+3<0},N={x|3﹣x>1},则M∩N=()A.{x|1<x<3}B.{x|1<x<2}C.∅D.{x|x<3}2.(5分)某校老年、中年和青年教师的人数见如表,采用分层插样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为()A.90B.100C.180D.3003.(5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.9B.18C.20D.354.(5分)重庆市2013年各月的平均气温(℃)数据的茎叶图如,则这组数据的中位数是()A.19B.20C.21.5D.235.(5分)在区间[0,2]上随机取一个实数x,若事件“3x﹣m<0”发生的概率为,则实数m=()A.1B.C.D.6.(5分)已知实数x,y满足则2x+y的最小值为()A.11B.3C.4D.27.(5分)已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是()A.B.ln(x2+1)>ln(y2+1)C.sin x>sin y D.x3>y38.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=.则下列结论中正确的个数为()①AC⊥BE;②EF∥平面ABCD;③三棱锥A﹣BEF的体积为定值;④△AEF的面积与△BEF的面积相等.A.1B.2C.3D.4二、填空题共6小题.9.(5分)已知函数f(x)=x+﹣3(x>0),则f(x)的最小值是.10.(5分)抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为.11.(5分)把红、黄、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人,事件“甲分得红牌”与“乙分得红牌”是.(填序号)①对立事件;②不可能事件;③互斥但不对立事件;④对立不互斥事件.12.(5分)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是.13.(5分)已知直线l⊥平面α,直线m⊆平面β,则下列四个命题:其中正确命题的序号是①若α∥β,则l⊥m;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.14.(5分)在平面上,过点P作直线l的垂线所得的垂足称为点P的直线上的投影,由区域中的点在直线x+y﹣2=0上的投影构成的线段记为AB,则|AB|=.三、解答题共5小题.解答应写出文字说明、演算步骤或证明过程.15.(10分)游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数,设两次记录的数分别为x,y,奖励规则如下:①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶,假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.(Ⅰ)求小亮获得玩具的概率;(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.16.(10分)如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC ⊥BC且AC=BC,O,M分别为AB,VA的中点.求证:(1)VB∥平面MOC;(2)OC⊥平面VAB.17.(10分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.18.(10分)如图所示,在正方体ABCD﹣A1B1C1D1中,M,N,E分别是AA1,AC,AB的中点,求证:(1)平面MEN∥平面A1BC;(2)A1C⊥C1D;(3)平面A1EC⊥平面A1CD.19.(10分)已知a∈R,函数f(x)=log2(+a).(1)当a=5时,解不等式f(x)>0;(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.(3)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.2016-2017学年北京市101中学高一(下)期末数学试卷参考答案与试题解析一、选择题共8小题.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合M={x|x2﹣4x+3<0},N={x|3﹣x>1},则M∩N=()A.{x|1<x<3}B.{x|1<x<2}C.∅D.{x|x<3}【解答】解:M={x|1<x<3},N={x|x<2};∴M∩N={x|1<x<2}.故选:B.2.(5分)某校老年、中年和青年教师的人数见如表,采用分层插样的方法调查教师的身体状况,在抽取的样本中,青年教师有320人,则该样本的老年教师人数为()A.90B.100C.180D.300【解答】解:由题意,老年和青年教师的人数比为900:1600=9:16,因为青年教师有320人,所以老年教师有180人,故选:C.3.(5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.9B.18C.20D.35【解答】解:初始值n=3,x=2,程序运行过程如下表所示:v=1i=2 v=1×2+2=4i=1 v=4×2+1=9i=0 v=9×2+0=18i=﹣1 跳出循环,输出v的值为18.故选:B.4.(5分)重庆市2013年各月的平均气温(℃)数据的茎叶图如,则这组数据的中位数是()A.19B.20C.21.5D.23【解答】解:样本数据有12个,位于中间的两个数为20,20,则中位数为,故选:B.5.(5分)在区间[0,2]上随机取一个实数x,若事件“3x﹣m<0”发生的概率为,则实数m=()A.1B.C.D.【解答】解:解不等式3x﹣m<0,可得x<,以长度为测度,则区间长度为,又在区间[0,2]上,∴区间长度为2,在区间[0,2]上随机取一个实数x,若事件“3x﹣m<0”发生的概率为,可得:,则m=1.故选:A.6.(5分)已知实数x,y满足则2x+y的最小值为()A.11B.3C.4D.2【解答】解:由已知得到平面区域如图:设z=2x+y,则y=﹣2x+z,由它在y轴的截距最小,得到z最小,解得A(2,1)由图可知当直线过A(2,1)时,z最小,所以最小值为5;故选:B.7.(5分)已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是()A.B.ln(x2+1)>ln(y2+1)C.sin x>sin y D.x3>y3【解答】解:∵实数x,y满足a x<a y(0<a<1),∴x>y,A.取x=2,y=﹣1,不成立;B.取x=0,y=﹣1,不成立C.取x=π,y=﹣π,不成立;D.由于y=x3在R上单调递增,因此正确故选:D.8.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=.则下列结论中正确的个数为()①AC⊥BE;②EF∥平面ABCD;③三棱锥A﹣BEF的体积为定值;④△AEF的面积与△BEF的面积相等.A.1B.2C.3D.4【解答】解:连结BD,则AC⊥平面BB1D1D,BD∥B1D1,∴AC⊥BE,EF∥平面ABCD,三棱锥A﹣BEF的体积为定值,从而A,B,C正确.∵点A、B到直线B1D1的距离不相等,∴△AEF的面积与△BEF的面积不相等,故D错误.故选:C.二、填空题共6小题.9.(5分)已知函数f(x)=x+﹣3(x>0),则f(x)的最小值是4﹣3.【解答】解:函数f(x)=x+﹣3(x>0)≥2﹣3=4﹣3,当且仅当x=2时,上式取得等号,则f(x)的最小值为4﹣3.故答案为:4﹣3.10.(5分)抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.【解答】解:由图表得到甲乙两位射击运动员的数据分别为:甲:87,91,90,89,93;乙:89,90,91,88,92;,.方差=4.=2.所以乙运动员的成绩较稳定,方差为2.故答案为2.11.(5分)把红、黄、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人,事件“甲分得红牌”与“乙分得红牌”是③.(填序号)①对立事件;②不可能事件;③互斥但不对立事件;④对立不互斥事件.【解答】解:根据题意,把红、黑、蓝、白4张纸牌随机地分发给甲、乙、丙、丁四个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”由互斥事件和对立事件的概念可判断两者不可能同时发生,故它们是互斥事件,又事件“乙取得红牌”与事件“丙取得红牌”也是可能发生的,事件“甲分得红牌”与事件“乙分得红牌”不是对立事件,故两事件之间的关系是互斥而不对立,故答案为:③12.(5分)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是.【解答】解:从1,2,3,4这四个数中一次随机取两个数,有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共6种情况;其中其中一个数是另一个的两倍的有两种,即(1,2),(2,4);则其概率为=;故答案为:.13.(5分)已知直线l⊥平面α,直线m⊆平面β,则下列四个命题:其中正确命题的序号是①③①若α∥β,则l⊥m;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.【解答】解:直线l⊥平面α,直线m⊂平面β,当α∥β,l⊥β,∴l⊥m,故①正确;当α⊥β,l∥β或l⊂β,∴l与m位置关系不确定,故②不正确;当l∥m,则m⊥α,∴α⊥β,故③正确;当l⊥m,则α∥β或α∩β,故④不正确,综上可知①③正确,故答案为:①③14.(5分)在平面上,过点P作直线l的垂线所得的垂足称为点P的直线上的投影,由区域中的点在直线x+y﹣2=0上的投影构成的线段记为AB,则|AB|=3.【解答】解:作出不等式组对应的平面区域如图:(阴影部分),区域内的点在直线x+y﹣2=0上的投影构成线段R′Q′,即SAB,而R′Q′=RQ,由得Q(﹣1,1)由即R(2,﹣2),则|AB|=|QR|==3,故答案为:3.三、解答题共5小题.解答应写出文字说明、演算步骤或证明过程.15.(10分)游乐场推出了一项趣味活动,参加活动者需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数,设两次记录的数分别为x,y,奖励规则如下:①若xy≤3,则奖励玩具一个;②若xy≥8,则奖励水杯一个;③其余情况奖励饮料一瓶,假设转盘质地均匀,四个区域划分均匀,小亮准备参加此项活动.(Ⅰ)求小亮获得玩具的概率;(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.【解答】解:(Ⅰ)两次记录的数为:(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,4),(2,1),(3,1),(4,1),(3,2),(3,3),(4,2),(4,3),(4,4),共16个,满足xy≤3,有(1,1),(1,2),(1,3),(2,1),(3,1),共5个,∴小亮获得玩具的概率为;(Ⅱ)满足xy≥8,(2,4),(3,4),(4,2),(4,3),(3,3),(4,4)共6个,∴小亮获得水杯的概率为;小亮获得饮料的概率为1﹣﹣=,∴小亮获得水杯大于获得饮料的概率.16.(10分)如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC ⊥BC且AC=BC,O,M分别为AB,VA的中点.求证:(1)VB∥平面MOC;(2)OC⊥平面VAB.【解答】证明:(1)因为O,M分别为AB,VA的中点,所以OM∥VB.又因为OM⊂平面MOC,VB⊄平面MOC,所以VB∥平面MOC.(2)因为AC=BC,O为AB的中点,所以OC⊥AB.又因为平面VAB⊥平面ABC,且OC⊂平面ABC,平面ABC∩平面VAB=AB,所以OC⊥平面VAB.17.(10分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.【解答】解:(Ⅰ)∵0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,∴a=0.3;(Ⅱ)由图可得月均用水量不低于3吨的频率为:0.5×(0.12+0.08+0.04)=0.12,由30×0.12=3.6得:全市居民中月均用水量不低于3吨的人数约为3.6万;(Ⅲ)由图可得月均用水量低于2.5吨的频率为:0.5×(0.08+0.16+0.3+0.4+0.52)=0.73<85%;月均用水量低于3吨的频率为:0.5×(0.08+0.16+0.3+0.4+0.52+0.3)=0.88>85%;则x=2.5+0.5×=2.9吨18.(10分)如图所示,在正方体ABCD﹣A1B1C1D1中,M,N,E分别是AA1,AC,AB的中点,求证:(1)平面MEN∥平面A1BC;(2)A1C⊥C1D;(3)平面A1EC⊥平面A1CD.【解答】证明:(1)因为M,N,E分别是AA1,AC,AB的中点,所以MN∥A1C,ME∥A1B.又因为MN∩ME=M,所以平面MEN∥平面A1BC.(2)因为BC⊥平面CDD1C1,C1D⊂平面CDD1∁l,所以BC⊥C1D.又在平面CDD l∁l中,C1D⊥CD1,BC∩CD1=C,所以C1D⊥平面BCD1A l,又因为A1C⊂平面BCD l A l,所以A1C⊥C1D.(3)连结A1D,取A1D中点F,取A1C中点O,连结AF,OF,OE,则AF⊥A1D.因为CD⊥平面A1AD,AF⊂平面A1AD,所以AF⊥CD,又C1D∩A1D=D,所以AF⊥平面A1CD,因为OF CD,EA CD,所以OF EA,所以四边形OF AE为平行四边形,所以EO∥AF,所以EO⊥平面A1CD,又EO⊂平面A1EC,所以平面A1EC⊥平面A1CD.19.(10分)已知a∈R,函数f(x)=log2(+a).(1)当a=5时,解不等式f(x)>0;(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a 的取值范围.(3)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.【解答】解:(1)当a=5时,f(x)=log2(+5),由f(x)>0;得log2(+5)>0,即+5>1,则>﹣4,则+4=>0,即x>0或x<﹣,即不等式的解集为{x|x>0或x<﹣}.(2)由f(x)﹣log2[(a﹣4)x+2a﹣5]=0得log2(+a)﹣log2[(a﹣4)x+2a﹣5]=0.即log2(+a)=log2[(a﹣4)x+2a﹣5],即+a=(a﹣4)x+2a﹣5>0,①则(a﹣4)x2+(a﹣5)x﹣1=0,即(x+1)[(a﹣4)x﹣1]=0,②,当a=4时,方程②的解为x=﹣1,代入①,成立当a=3时,方程②的解为x=﹣1,代入①,成立当a≠4且a≠3时,方程②的解为x=﹣1或x=,若x=﹣1是方程①的解,则+a=a﹣1>0,即a>1,若x=是方程①的解,则+a=2a﹣4>0,即a>2,则要使方程①有且仅有一个解,则1<a≤2.综上,若方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,则a的取值范围是1<a≤2,或a=3或a=4.(3)函数f(x)在区间[t,t+1]上单调递减,由题意得f(t)﹣f(t+1)≤1,即log2(+a)﹣log2(+a)≤1,即+a≤2(+a),即a≥﹣=设1﹣t=r,则0≤r≤,==,当r=0时,=0,当0<r≤时,=,∵y=r+在(0,)上递减,∴r+≥=,∴==,∴实数a的取值范围是a≥.。

2016-2017学年北京师范大学附属中学高一下学期期末考试数学试题一、单选题1.若实数,满足,则下列不等式一定成立的是().A. B. C. D.【答案】D【解析】分析:灵活选择方法逐一判断正误.详解:对于选项A,令a=3,b=2,则,所以选项A不一定成立;对于选项B,令a=0,b=-1,则没有意义,所以选项B不一定成立;对于选项C,令a=0,b=-2,则,所以选项C不一定成立;对于选项D,是增函数,因为a>b,所以.故答案为:D点睛:(1)本题主要考查不等式的基本性质,意在考查学生对这些基础知识的掌握水平和思维的灵活性.(2)类似这种不等关系真假的判断,方法比较灵活,有的可以举反例,有的可以直接证明,要结合具体题目灵活选择.2.对变量,由观测数据理据得散点图:对变量,有观测数据,的散点图,由这两个散点图可以判断().A. 变量与正相关,与正相关B. 变量与正相关,与负相关C. 变量与负相关,与正相关D. 变量与负相关,与负相关【答案】C【解析】试题分析:由题图1可知,y随x的增大而减小,各点整体呈下降趋势,x与y 负相关,由题图2可知,u随v的增大而增大,各点整体呈上升趋势,u与v正相关【考点】散点图3.从甲、乙两个城市分别随机抽取台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为,,中位数分别为,,则().A. ,B. ,C. ,D. ,【答案】B【解析】甲的平均数甲= (5+6+8+10+10+14+18+18+22+25+27+30+30+38+41+43)=,乙的平均数乙= (10+12+18+20+22+23+23+27+31+32+34+34+38+42+43+48)=,所以.甲的中位数为20,乙的中位数为29,所以m甲<m乙,故选:B.4.执行下面的程序框图,如果输入,那么输出的的值为().A. B. C. D.【答案】B【解析】:由程序框图可顺次得数据如下:,输出为【考点定位】本题考查程序框图的识别与运算,要注意控制变量在运算过程中的作用,题目中较之以前练习过的题目多出一步比较运算,使试题具有一定难度5.公差不为零的等差数列的第项、第项、第项恰好构成等比数列,则它的公比为().A. B. C. D.【答案】C【解析】设等差数列的首项为,公差为,由等比数列的性质可得,整理可得,6.下列命题中正确的是().A. 若两条直线都平行与同一个平面,则这两条直线平行B. 过一条直线有且只有一个平面与已知平面垂直C. 若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面D. 若这两条直线垂直于同一个平面,则这两个直线共面【答案】D【解析】(A)平行于同一平面的两条直线相交、平行或异面,故错;(B)当直线垂直于已知平面时,过该直线的无数个平面与已知平面都垂直,故错;(C)该直线可能在平面内,故错;故选D。

2016-2017学年北京大学附中荣誉班高一(下)期末数学试卷一、填空题(每空4分,共10空,40分)1.(4分)在△ABC中,,,A=30°,则边长c=.2.(4分)已知数列{a n}的前n项和S n满足S n=2a n+1,则a2017=.3.(4分)已知二维直角坐标系中的点A坐标为(a,a2﹣3a+2),a∈R,则A不可能在第象限.4.(4分)由,x>0的最小值是2,,x>0的最小值是,,x>0的最小值是,可以归纳出,x>0的最小值是.5.(4分)设地球的半径长度为单位1,地球表面上的两点A、B位于北纬45°的纬线圈上,其经度分别为东经150°、西经120°,则这两个点的球面距离为.6.(4分)如图为某空间几何体的三视图,则该几何体的体积为:.7.(4分)对于直线a、b和平面α,以下四个命题中正确的个数为个:①若a∥α,b∥a,则b∥α;②若a⊂α,b∩α={A},则a与b异面;③若a∥b,b⊥α,则a⊥α;④若a⊥b,a⊥α,b⊄α,则b∥α.8.(4分)直线ax+9y﹣6=0与直线x+ay﹣2=0平行,则a=.9.(4分)在平面直角坐标系中,动点A到点(0,﹣3)的距离不大于2,则A到原点距离的最大值为.10.(4分)在平面直角坐标系中,已知圆A过直线y=x和圆x2+y2=4的交点,且被交点所在的弦在圆A中所对的圆心角为,则圆A的标准方程为.二、解答题(共6题,70分,其中第6题为附加题.只写结果不写过程不得分)11.(12分)设数列{a n}的首项a1=a≠﹣2,且满足关系:,(1)求a2,a3.(2)设b n=a2n﹣1+2,证明{b n}为等比数列并求其通项公式.(3)求数列{a n}的通项公式.12.(12分)已知函数的最小值为3.(1)求a的值.(2)解不等式f(x)>5.13.(12分)已知如图所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED ⊥平面ABCD,.(1)求证:平面BCF∥平面AED.(注意排除重合情况)(2)若BF=BD=a,求四棱锥A﹣BDEF的体积.14.(11分)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE =2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE.15.(13分)如图,在底面是矩形的四棱锥P﹣ABCD中,P A⊥平面ABCD,P A=AB=2,BC=4.E是PD的中点,(1)求二面角E﹣AC﹣D的余弦值;(2)求直线CD与平面AEC所成角的正弦值.16.(10分)在以下两个题目当中任选1题作答(解答时需注明所选题目):(1)写出三元均值不等式的形式并证明.(默认已知二元均值不等式)(2)证明半径已知的球面上两个定点之间所构成的圆弧(圆弧位于已知球表面)中,大圆所对应的劣弧最短.(提示:取倒数、利用锐角θ满足sinθ<θ<tanθ证明.此题如果用导数证明将酌情减分)2016-2017学年北京大学附中荣誉班高一(下)期末数学试卷参考答案与试题解析一、填空题(每空4分,共10空,40分)1.(4分)在△ABC中,,,A=30°,则边长c=2或.【解答】解:∵,,A=30°,∴由正弦定理可得:sin B===,∵a<b,∴30°=A<B,可得:B=60°或120°当B=60°时,C=90°,则c==2,当b=120°时,C=30°,则c=a=.故答案为:2或.2.(4分)已知数列{a n}的前n项和S n满足S n=2a n+1,则a2017=﹣22016.【解答】解:∵S n=2a n+1,∴n≥2时,a n=S n﹣S n﹣1=2a n+1﹣(2a n﹣1+1),化为:a n=2a n.﹣1n=1时,a1=2a1+1,解得a1=﹣1.∴数列{a n}是等比数列,首项为﹣1,公比为2.则a2017=﹣22016.故答案为:﹣22016.3.(4分)已知二维直角坐标系中的点A坐标为(a,a2﹣3a+2),a∈R,则A不可能在第三象限.【解答】解:令f(a)=a2﹣3a+2=﹣,a>0时,A可以在第一,四象限或在x轴的正半轴上,a=0时,A在y轴的上半轴上,a<0时,A在第二象限,故A不可能在第三象限,故答案为:三.4.(4分)由,x>0的最小值是2,,x>0的最小值是,,x>0的最小值是,可以归纳出,x>0的最小值是.【解答】解:由,x>0的最小值是=2,,x>0的最小值是3=,,x>0的最小值是4=,可以归纳出,x>0的最小值是(n+1)=.故答案为:.5.(4分)设地球的半径长度为单位1,地球表面上的两点A、B位于北纬45°的纬线圈上,其经度分别为东经150°、西经120°,则这两个点的球面距离为.【解答】解:设北纬45°纬线圈圆心为M,地球球心为O,∵A,B在北纬45°纬线圈上,∴∠AOM=∠BOM=45°,又OM⊥AM,OM⊥BM,∴AM=BM=OA=,∵A,B经度分别为东经150°、西经120°,∴∠AMB=90°,∴AB=AM=1,∴△OAB是边长为1的等边三角形,∴AB的球面距离为×OA=.故答案为:.6.(4分)如图为某空间几何体的三视图,则该几何体的体积为:.【解答】解:由已知三视图得到几何体是正方体挖去一个圆锥,其中正方体的棱长为2,圆锥的底面直径为2,高为2,由此得到几何体的体积为;故答案为:.7.(4分)对于直线a、b和平面α,以下四个命题中正确的个数为③④个:①若a∥α,b∥a,则b∥α;②若a⊂α,b∩α={A},则a与b异面;③若a∥b,b⊥α,则a⊥α;④若a⊥b,a⊥α,b⊄α,则b∥α.【解答】对于①,若a∥α,b∥a,则b与α的位置关系不能确定,故错;对于②,若a⊂α,b∩α={A},当A∈a时,a与b相交,共面,故错对于③,若a∥b,b⊥α,则a⊥α,根据线面垂直的判定可得③正确;对于④,若a⊥b,a⊥α,b⊄α,则b∥α.根据线面平行的判定可得④正确:故答案为:③④8.(4分)直线ax+9y﹣6=0与直线x+ay﹣2=0平行,则a=﹣3.【解答】解:由a2﹣9=0,解得a=±3.经过验证a=3时两条直线重合,舍去.∴a=﹣3.故答案为:﹣3.9.(4分)在平面直角坐标系中,动点A到点(0,﹣3)的距离不大于2,则A到原点距离的最大值为5.【解答】解:由题意,动点A到点(0,﹣3)的距离不大于2,可得方程为x2+(x+3)2≤4,即以点(0,﹣3)为圆心,半径r=2.圆上一点到原点距离的最大值为:3+2=5.故答案为:5.10.(4分)在平面直角坐标系中,已知圆A过直线y=x和圆x2+y2=4的交点,且被交点所在的弦在圆A中所对的圆心角为,则圆A的标准方程为(x﹣)2+(y+)2=16或(x+)2+(y﹣)2=16.【解答】解:由题意,圆A过直线y=x和圆x2+y2=4的交点,那么圆心在直线y=﹣x上,弦长d=2,设圆心(a,﹣a),被交点所在的弦在圆A中所对的圆心角为,∴r=4圆心到直线x﹣y=0的距离d==,解得a=.半径r=4.∴得圆A的标准方程为(x﹣)2+(y+)2=16或(x+)2+(y﹣)2=16.故答案为:(x﹣)2+(y+)2=16或(x+)2+(y﹣)2=16.二、解答题(共6题,70分,其中第6题为附加题.只写结果不写过程不得分)11.(12分)设数列{a n}的首项a1=a≠﹣2,且满足关系:,(1)求a2,a3.(2)设b n=a2n﹣1+2,证明{b n}为等比数列并求其通项公式.(3)求数列{a n}的通项公式.【解答】(1)解:∵数列{a n}的首项a1=a≠﹣2,且满足关系:,∴a2=a1+1=a+1.a3=2a2=2(a+1).(2)证明:n≥2时,b n=a2n﹣1+2=2a2n﹣2+2=2(a2n﹣3+1)+2=2(a2n﹣3+2)=2b n﹣1,b1=a1+2=a+2≠0.∴{b n}为等比数列,公比为2,首项为a+2.∴b n=(a+2)•2n﹣1.(3)解:由(2)可得:b n=a2n﹣1+2=(a+2)•2n﹣1.∴a2n﹣1=(a+2)•2n﹣1﹣2,(n≥2).a2n=a2n﹣1+1=a2n﹣1+1=(a+2)•2n﹣1﹣1,∴a n=.12.(12分)已知函数的最小值为3.(1)求a的值.(2)解不等式f(x)>5.【解答】解:(1)f(x)=x2+=x2++≥3=3,当且仅当x=时取等号,∵f(x)=x2+的最小值为3,∴3=3,解得a=2,(2)∵f(x)=x2+>5,∴x3﹣5x+2>0,∴x3﹣4x﹣x+2>0,即x(x+2)(x﹣2)﹣(x﹣2)=(x﹣2)(x2+2x﹣1)=(x﹣2)(x+1+)(x+1﹣)>0,即(x﹣2)(x+1﹣)>0,解得x>2或0<x<﹣1,故不等式的解集为(0,﹣1)∪(2,+∞)13.(12分)已知如图所示的多面体中,四边形ABCD是菱形,四边形BDEF是矩形,ED ⊥平面ABCD,.(1)求证:平面BCF∥平面AED.(注意排除重合情况)(2)若BF=BD=a,求四棱锥A﹣BDEF的体积.【解答】(1)证明:∵ABCD是菱形,∴BC∥AD,∵BC⊄面ADE,AD⊂面ADE,∴BC∥面ADE,∵BDEF是矩形,∴BF∥DE,∵BF⊄面ADE,DE⊂面ADE,∴BF∥面ADE,∵BC⊂面BCF,BF⊂面BCF,BC∩BF=B,∴面BCF∥面ADE;(2)解:连接AC,AC∩BD=O,∵ABCD是菱形,∴AC⊥BD,∵ED⊥面ABCD,AC⊂面ABCD,∴ED⊥AC,∵ED,BD⊂面BDEF,ED∩BD=D,∴AO⊥面BDEF,∴AO为四棱锥A﹣BDEF的高.由ABCD是菱形,∠BAD=,得△ABD为等边三角形,由BF=BD=a,得AD=a,AO=,∴•a2•=.14.(11分)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE =2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE.【解答】解(1)证明:取CE的中点G,连FG、BG.∵F为CD的中点,∴GF∥DE且GF=DE.∵AB⊥平面ACD,DE⊥平面ACD,∴AB∥DE,∴GF∥AB.又AB=DE,∴GF=AB.∴四边形GF AB为平行四边形,则AF∥BG.∵AF⊄平面BCE,BG⊂平面BCE,∴AF∥平面BCE.(2)∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.∵DE⊥平面ACD,AF⊂平面ACD,∴DE⊥AF.又CD∩DE=D,故AF⊥平面CDE.∵BG∥AF,∴BG⊥平面CDE.∵BG⊂平面BCE,∴平面BCE⊥平面CDE.15.(13分)如图,在底面是矩形的四棱锥P﹣ABCD中,P A⊥平面ABCD,P A=AB=2,BC=4.E是PD的中点,(1)求二面角E﹣AC﹣D的余弦值;(2)求直线CD与平面AEC所成角的正弦值.【解答】解:以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),E(0,2,1),P(0,0,2).∴=(2,0,0),=(0,4,0),=(0,0,2),=(﹣2,0,0),=(0,2,1),=(2,4,0).(1)设平面AEC的法向量=(x,y,z),令z=1,则=(x,y,1).由即,解得∴=(1,,1).平面ABC的法向量=(0,0,2).cos===.所以二面角E﹣AC﹣D所成平面角的余弦值是.(2)因为平面AEC的法向量是=(1,,1),而=(﹣2,0,0).所以cosθ===﹣.直线CD与平面AEC的正弦值.16.(10分)在以下两个题目当中任选1题作答(解答时需注明所选题目):(1)写出三元均值不等式的形式并证明.(默认已知二元均值不等式)(2)证明半径已知的球面上两个定点之间所构成的圆弧(圆弧位于已知球表面)中,大圆所对应的劣弧最短.(提示:取倒数、利用锐角θ满足sinθ<θ<tanθ证明.此题如果用导数证明将酌情减分)【解答】选(1).解:(1)求证:对于正数:a,b,c∈N+,则:,证明:只要证明对于正数:a,b,c∈N+,a3+b3+c3≥3abc成立即可.由于:a3+b3+c3﹣3abc,=(a+b)3﹣3a2b﹣3ab2﹣3abc+c3,=(a+b+c)[(a+b)2﹣(a+b)c+c2]﹣3ab(a+b+c),=(a+b+c)(a2+b2+c2﹣ab﹣ac﹣bc),=(a+b+c)[(a﹣b)2+(b﹣c)2+(c﹣a)2]≥0,故:a3+b3+c3≥3abc,所以:=3,即:.。
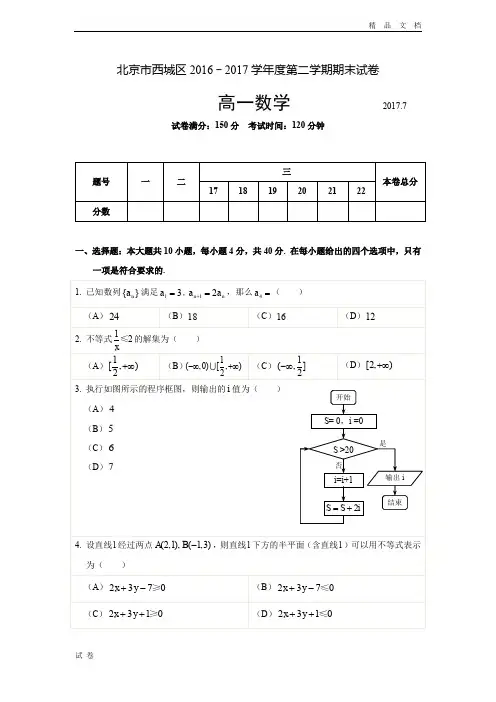
北京市西城区2016 - 2017学年度第二学期期末试卷高一数学2017.7试卷满分:150分考试时间:120分钟一、选择题:本大题共10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项是符合要求的.1[,)+∞2执行如图所示的程序框图,则输出的i值为(二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 11. 函数()f x _______.12. 在等差数列{}n a 中,245a a +=,则3a =_______.13. 随机抽取某班6名学生,测量他们的身高(单位:cm ),获得身高数据依次为:162,168,170,171,179,182,那么此班学生平均身高大约为 cm ;样本数据的方差为 .14. 设x ,y 满足约束条件2,1,10,y x x y y ++⎧⎪⎨⎪⎩≤≤≥ 则3z x y =+的最大值是_______.15. 有4张卡片,上面分别写有0,1,2,3. 若从这4张卡片中随机取出2张组成一个两位数,则此数为偶数的概率是_______.16. 在数列{}n a 中,312a =,115a =-,且任意连续三项的和均为11,则2017a =_______;设n S 是数列{}n a 的前n 项和,则使得100n S ≤成立的最大整数n =_______.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分13分)在等差数列{}n a 中,12a =,3516a a +=. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)如果2a ,m a ,2m a 成等比数列,求正整数m 的值.18.(本小题满分13分)北京是我国严重缺水的城市之一.为了倡导“节约用水,从我做起”,小明在他所在学校的2000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:[2,4),[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图.(Ⅰ)给出图中实数a 的值;(Ⅱ)根据样本数据,估计小明所在学校2000名同学家庭中,月均用水量低于8吨的约有多少户;(Ⅲ)在月均用水量大于或等于10吨的样本数据中,小明决定随机抽取2名同学家庭进行访谈,求这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组的概率.19.(本小题满分13分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且2a =,1cos 4C =-. (Ⅰ)如果3b =,求c 的值;(Ⅱ)如果c =sin B 的值.20.(本小题满分13分)已知数列{}n a 的前n 项和24n S n n =-,其中*n ∈N .吨a(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设21na nb =+,求数列{}n b 的前n 项和n T ;(Ⅲ)若对于任意正整数n ,都有12231111n n a a a a a a λ++++≤,求实数λ的最小值.21.(本小题满分14分)已知函数2()(21)f x ax a x b =+++,其中a ,b ∈R .(Ⅰ)当1a =,4b =-时,求函数()f x 的零点;(Ⅱ)如果函数()f x 的图象在直线2y x =+的上方,证明:2b >; (Ⅲ)当2b =时,解关于x 的不等式()0f x <.22.(本小题满分14分)在无穷数列{}n a 中,1a p =是正整数,且满足1, ,25, .nn n nn a a a a a +⎧⎪=⎨⎪+⎩当为偶数当为奇数 (Ⅰ)当39a =时,给出p 的值;(结论不要求证明) (Ⅱ)设7p =,数列{}n a 的前n 项和为n S ,求150S ;(Ⅲ)如果存在*m ∈N ,使得1m a =,求出符合条件的p 的所有值.北京市西城区2016-2017学年度第二学期期末试卷高一数学参考答案及评分标准2017.7一、选择题:本大题共10小题,每小题4分,共40分.1. A2. B3. B4. B5. D6. A7. C8. D9. C 10. C二、填空题:本大题共6小题,每小题5分,共30分.11. [2,2]-; 12.52; 13. 172,45; 14. 73; 15. 59; 16. 4,29.注:一题两空的题目,第一空2分,第二空3分. 三、解答题:本大题共6小题,共80分. 17.(本小题满分13分)(Ⅰ)解:设等差数列{}n a 的公差为d ,则3512616a a a d +=+=, ………………………3分 又因为12a =,解得2d =. ………………………5分 所以1(1)2n a a n d n =+-=. ………………………7分 (Ⅱ)解:因为2a ,m a ,2m a 成等比数列,所以222m m a a a =⋅, ………………………10分即2(2)44m m =⨯,m *∈N ,解得4m =. ………………………13分18.(本小题满分13分)(Ⅰ)解:因为各组的频率之和为1,所以月均用水量在区间[10,12)的频率为 1(0.02520.0750.1000.225)20.1-⨯+++⨯=,所以,图中实数0.120.050a =÷=. ………………………3分 (Ⅱ)解:由图可知, 样本数据中月均用水量低于8吨的频率为(0.0250.0750.225)20.65++⨯=, ………………………5分所以小明所在学校2000名同学家庭中,月均用水量低于8吨的约有0.6520001300⨯=(户). ………………………7分(Ⅲ)解:设“这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组”为事件A , 由图可知, 样本数据中月均用水量在[10,12)的户数为0.0502404⨯⨯=.记这四名同学家庭分别为,,,a b c d ,月均用水量在[12,14]的户数为0.0252402⨯⨯=.记这两名同学家庭分别为,e f , 则选取的同学家庭的所有可能结果为:(,),(,),(,),(,),(,),(,),(,),a b a c a d a e a f b c b d (,),(,),(,),(,),(,),(,),(,),(,),b e b f c d c e c f d e d f e f 共15种, ………………………9分事件A 的可能结果为:(,),(,),(,),(,),a e a f b e b f (,),(,),(,),(,),c e c f d e d f 共8种, ………………………11分 所以8()15P A =. ………………………13分19.(本小题满分13分)(Ⅰ)解:由余弦定理2222cos c a b ab C =+-, ………………………3分 得2149223()164c =+-⨯⨯⨯-=,解得4c =. ………………………5分(Ⅱ)解:(方法一)由1cos 4C =-,(0,π)C ∈,得sin C ==.……7分由正弦定理sin sin a c A C =,得sin sin 8a C A c ==. ……………………10分所以cos 8A ==. 因为πABC ++=,所以sin sin()B A C =+sin cos cos sin A C A C =+ ………………………12分1()4-+=. ………………………13分(方法二)由1cos 4C =-,(0,π)C ∈,得sin C …………7分 由余弦定理2222cos c a b ab C =+-, 得2124422()4b b =+-⨯⨯⨯-,解得4b =,或5b =-(舍). ………………………10分由正弦定理sin sin b c B C =,得sin sin 4b C Bc ==. ………………………13分20.(本小题满分13分)(Ⅰ)解:当1n =时,113a S ==-; ………………………1分 当2n ≥时,125n n n a S S n -=-=-, ………………………3分 因为13a =-符合上式,所以25n a n =-*()n ∈N . ………………………4分 (Ⅱ)解:由(Ⅰ),得2521n n b -=+. ………………………5分 所以12n n T b b b =+++3125(21)(21)(21)n ---=++++++3125(222)n n ---=++++ ………………………6分32(14)14n n --=+-1(41)24n n =-+. ………………………9分(Ⅲ)解:122311111111131335(25)(23)n n a a a a a a n n +=-++++⨯⨯--+++2111111[(1)()()]323352523n n =-+-+-++---11646n =---, ………………………11分 当1n =时,12113a a =,(注:此时1046n <-) 由题意,得13λ≥; ………………………12分 当2n ≥时, 因为1046n >-, 所以1223111116n n a a a a a a +<-+++. 因为对于任意正整数n ,都有12231111n n a a a a a a λ++++≤,所以λ的最小值为13. ………………………13分21.(本小题满分14分)(Ⅰ)解:由2()340f x x x =+-=,解得4x =-,或1x =.所以函数()f x 有零点4-和1. ………………………3分 (Ⅱ)解:(方法1)因为()f x 的图象在直线2y x =+的上方,所以2(21)2ax a x b x +++>+对x ∈R 恒成立.即2220ax ax b ++->对x ∈R 恒成立. ………………………5分所以当0x =时上式也成立,代入得2b >. ………………………8分 (方法2)因为()f x 的图象在直线2y x =+的上方, 所以2(21)2ax a x b x +++>+对x ∈R 恒成立.即2220ax ax b ++->对x ∈R 恒成立. ………………………5分 当0a =时,显然2b >. 当0a ≠时,由题意,得0a >,且2(2)4(2)0a a b ∆=--<, ………………………6分 则24(2)40a b a ->>, 所以4(2)0a b ->,即2b >.综上,2b >. ………………………8分(Ⅲ)解:由题意,得不等式2(21)20ax a x +++<,即(1)(2)0ax x ++<. …………9分当0a =时,不等式化简为20x +<,解得2x <-; ………………………10分 当0a ≠时,解方程(1)(2)0ax x ++=,得根12x =-,21x a=-. 所以,当0a <时,不等式的解为:2x <-,或1x a>-; ………………………11分 当102a <<时,不等式的解为:12x a -<<-; ………………………12分当12a =时,不等式的解集为∅; ………………………13分当12a >时,不等式的解为:12x a-<<-. ………………………14分 综上,当0a <时,不等式的解集为{|2x x <-,或1}x a >-;当0a =时,不等式的解集为{|2}x x <-;当102a <<时,不等式的解集为1{|2}x x a -<<-;当12a =时,不等式的解集为∅;当12a >时,不等式的解集为1{|2}x x a-<<-.22.(本小题满分14分)(Ⅰ)解:36p =,或13. ………………………3分 (Ⅱ)解:由题意,17a =,代入,得212a =,36a =,43a =,58a =,64a =,72a =,81a =,96a =,所以数列{}n a 中的项,从第三项起每隔6项重复一次(注:39a a =), ………5分 故15012348345624()S a a a a a a a a a =+++++++++71224(638421)6384=+++++++++++ 616=.………………………8分(Ⅲ)解:由数列{}n a 的定义,知*n a ∈N .设t 为数列{}n a 中最小的数,即min{}i t a i =∈N *, 又因为当n a 为偶数时,12nn a a +=, 所以t 必为奇数. ………………………9分 设k a t =,则15k a t +=+,252k t a ++=, 所以52t t +≤,解得5t ≤. 所以{1,3,5}t ∈. ………………………10分 如果3k a t ==,那么由数列{}n a 的定义,得18k a +=,24k a +=,32k a +=,41k a +=, 这显然与3t =为{}n a 中最小的数矛盾,所以3t ≠. ………………………12分精品文档试卷如果5ka t==,当1k=时,5p=;当2k≥时,由数列{}na的定义,得1ka-能被5整除,…,得1a p=被5整除;所以当且仅当*15()a p r r==∈N时,5t=. ………………………13分这与题意不符.所以当*15()a r r≠∈N时,数列{}na中最小的数1t=,即符合条件的p值的集合是*{|r r∈N,且r不能被5整除}. …………………14分。

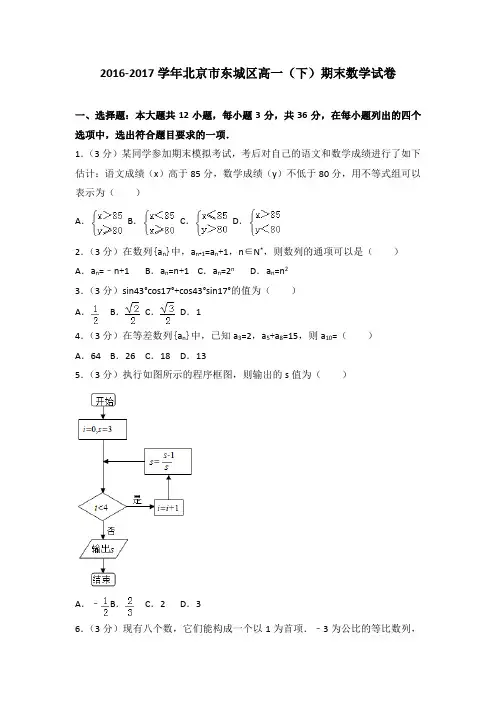
2016-2017学年北京市东城区高一(下)期末数学试卷一、选择题:本大题共12小题,每小题3分,共36分,在每小题列出的四个选项中,选出符合题目要求的一项.1.(3分)某同学参加期末模拟考试,考后对自己的语文和数学成绩进行了如下估计:语文成绩(x)高于85分,数学成绩(y)不低于80分,用不等式组可以表示为()A.B.C.D.2.(3分)在数列{a n}中,a n+1=a n+1,n∈N*,则数列的通项可以是()A.a n=﹣n+1 B.a n=n+1 C.a n=2n D.a n=n23.(3分)sin43°cos17°+cos43°sin17°的值为()A.B.C.D.14.(3分)在等差数列{a n}中,已知a3=2,a5+a8=15,则a10=()A.64 B.26 C.18 D.135.(3分)执行如图所示的程序框图,则输出的s值为()A.﹣ B.C.2 D.36.(3分)现有八个数,它们能构成一个以1为首项.﹣3为公比的等比数列,若从这八个数中随机抽取一个数,则它大于8的概率是()A.B.C.D.7.(3分)若不等式m<n与<(m,n为实数)同时成立,则()A.m<n<0 B.0<m<n C.m<0<n D.mn>08.(3分)欲测量河宽即河岸之间的距离(河的两岸可视为平行),受地理条件和测量工具的限制,采用如下办法:如图所示,在河的一岸边选取A,B两个观测点,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,AB=120米,由此可得河宽约为(精确到1米,参考数据≈2.45,sin75°≈0.97)()A.170米B.110米C.95米D.80米9.(3分)已知{a n}为等比数列,S n为其前n项和.a3﹣a1=15,a2﹣a1=5,则S4=()A.75 B.80 C.155 D.16010.(3分)甲、乙、丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图所示若s甲,s乙,s丙分别表示他制测试成绩的标准差,则它们的大小关系为()A.s丙<s甲<s乙B.s甲<s丙<s乙C.s乙<s丙<s甲D.s丙<s乙<s甲11.(3分)若在区间[0,2]中随机地取两个数,则这两个数中较小的数大于的概率是()A.B.C.D.12.(3分)已知数列2016,2017,1,﹣2016,﹣2017,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2017项之和等于()A.0 B.2016 C.2017 D.4033二、填空题:本大题共6小题,每小题3分,共l8分将答案填在题中横线上.13.(3分)不等式2x2﹣x≤0的解集为.14.(3分)某校高一年级三个班共有学生120名,这三个班的男、女生人数如下表.已知在全年级学生中随机抽取1人,抽到二班女生的概率是0.2.则x=;现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为.15.(3分)小亮开通了一个微信公众号,每天推送一篇文章,通常将阅读量作为微信公众号受关注度的评判标准,为了提升公众号的关注度,进一步了解大家的需求,小亮对之前推送的100篇文章的阅读量进行了统计,得到如下的频率分布直方图:则图中的a=.16.(3分)当x>0时,不等式x+≥a恒成立,则实数a的取值范围是.17.(3分)已知数列{a n}的前n项和为S n,且a n+S n=1,n∈N*,则a1=;a n=.18.(3分)某共享单车公司欲在某社区投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型为运动型,成本为500元/车,骑行半小时需花费0.5元;B型车为轻便型,成本为3000元/车,骑行半小时需花费1元.若公司投入成本资金不能超过10万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时(不足半小时按半小时计算),则在该社区单车公司可获得的总收入最多为元.三、解答题:本大题共5小题,共46分,解答应写出文字说明、证明过程或演算步骤.19.(7分)如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.(1)求∠ADC的大小;(2)求AB的长.20.(7分)已知{a n}为等差数列,a1=﹣12,a5=2a6.(I)求数列{a n}的通项公式以及前n项和S n.(Ⅱ)求使得S n>14的最小正整数n的值.21.(10分)已知sinα﹣2cosα=0.(I)求tan(α+)的值.(Ⅱ)求的值.22.(10分)长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.23.(12分)已知函数f(x),给出如下定义:若f1(x),f2(x),…,f n(x),…(x)),其中均为定义在同一个数集下的函数,且f1(x)=f(x),f n(x)=f(f n﹣1n=2,3,4,…,则称f1(x),f2(x),…,f n(x),…为一个嵌套函数列,记为{f n(x)=λf n(x),(x)},若存在非零实数λ,使得嵌套函数列{f n(x)}满足f n﹣1则称{f n(x)}为类等比函数列.(Ⅰ)已知{f n(x)}是定义在R上的嵌套函数列,若f(x)=+.①求f(2),f2(2),f3(2).②证{f n(x)﹣}是类等比函数列.(Ⅱ)已知{g n(x)}是定义在(1,+∞)上嵌套函数列.(x)﹣g n(x)|<|x﹣|.若g(x)=(x+),求证|g n+12016-2017学年北京市东城区高一(下)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题3分,共36分,在每小题列出的四个选项中,选出符合题目要求的一项.1.(3分)某同学参加期末模拟考试,考后对自己的语文和数学成绩进行了如下估计:语文成绩(x)高于85分,数学成绩(y)不低于80分,用不等式组可以表示为()A.B.C.D.【解答】解:∵语文成绩(x)高于85分,数学成绩(y)不低于80分,∴,故选:A.2.(3分)在数列{a n}中,a n+1=a n+1,n∈N*,则数列的通项可以是()A.a n=﹣n+1 B.a n=n+1 C.a n=2n D.a n=n2=a n+1,n∈N*,【解答】解:∵a n+1∴a n﹣a n=1,n∈N*,+1∴数列{a n}为公差为1的等差数列,其中A,a n=﹣n+1中,a n+1﹣a n=﹣(n+1)+1+n﹣1=﹣1,不满足,B,a n=n+1中,a n+1﹣a n=(n+1)+1+n﹣1=1,满足,C:为等比数列,不满足,D:a n+1﹣a n=(n+1)2﹣n2=2n+1,不满足,故选:B.3.(3分)sin43°cos17°+cos43°sin17°的值为()A.B.C.D.1【解答】解:sin43°cos17°+cos43°sin17°=sin(43°+17°)=sin60°=,故选:C.4.(3分)在等差数列{a n}中,已知a3=2,a5+a8=15,则a10=()A.64 B.26 C.18 D.13【解答】解:设公差为d,a3=2,a5+a8=15,∴a3+2d+a3+5d=15,解得7d=11,∴a10=a3+7d=2+11=13,故选:D.5.(3分)执行如图所示的程序框图,则输出的s值为()A.﹣ B.C.2 D.3【解答】解:i=0<4,s=3,i=1<4,s=,i=2,s=﹣,i=3<4,s=3,i=4≥4,输出s=3,故选:D.6.(3分)现有八个数,它们能构成一个以1为首项.﹣3为公比的等比数列,若从这八个数中随机抽取一个数,则它大于8的概率是()A.B.C.D.【解答】解:由题意成等比数列的8个数为:1,﹣3,(﹣3)2,(﹣3)3…(﹣3)7;其中大于8的项有:(﹣3)2,(﹣3)4,(﹣3)6,共3个数这8个数中随机抽取一个数,则它大于8的概率是P=;故选:D.7.(3分)若不等式m<n与<(m,n为实数)同时成立,则()A.m<n<0 B.0<m<n C.m<0<n D.mn>0【解答】解:∵m<n与<(m,n为实数)同时成立,∴只有mn<0时,=<0.∴m<0<n.故选:C.8.(3分)欲测量河宽即河岸之间的距离(河的两岸可视为平行),受地理条件和测量工具的限制,采用如下办法:如图所示,在河的一岸边选取A,B两个观测点,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,AB=120米,由此可得河宽约为(精确到1米,参考数据≈2.45,sin75°≈0.97)()A.170米B.110米C.95米D.80米【解答】解:在△ABC中,∠ACB=180°﹣75°﹣45°=60°,由正弦定理得:,∴AC===40,∴S△ABC=AB•AC•sin∠CAB=≈5703.6,∴C到AB的距离d==≈95.故选:C.9.(3分)已知{a n}为等比数列,S n为其前n项和.a3﹣a1=15,a2﹣a1=5,则S4=()A.75 B.80 C.155 D.160【解答】解:∵a3﹣a1=15,a2﹣a1=5,由等比数列的通项,可得a1q2﹣a1=15,a1q﹣a1=5,∵a2﹣a1≠0,∴q≠1解得:a1=5,q=2.那么:S4=a1+a2+a3+a4==75.故选:A.10.(3分)甲、乙、丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图所示若s甲,s乙,s丙分别表示他制测试成绩的标准差,则它们的大小关系为()A.s丙<s甲<s乙B.s甲<s丙<s乙C.s乙<s丙<s甲D.s丙<s乙<s甲【解答】解:甲的平均成绩为(7+8+9+10)×0.25=8.5,其方差为S甲2=0.25×[(7﹣8.5)2+(8﹣8.5)2+(9﹣8.5)2+(10﹣8.5)2]=1.25乙的平均成绩为7×0.3+8×0.2+9×0.2+10×0.3=8.5,其方差为S乙2=0.3×(7﹣8.5)2+0.2×(8﹣8.5)2+0.2×(9﹣8.5)2+0.3×(10﹣8.5)2=1.45丙的平均成绩为7×0.2+8×0.3+9×0.3+10×0.2=8.5,其方差为S丙2=0.2×(7﹣8.5)2+0.3×(8﹣8.5)2+0.3×(9﹣8.5)2+0.2×(10﹣8.5)2=1.05∴S丙2<S甲2<S乙2∴S丙<S甲<S乙.故选:A.11.(3分)若在区间[0,2]中随机地取两个数,则这两个数中较小的数大于的概率是()A.B.C.D.【解答】解:在区间[0,2]中随机地取一个数,这两个数中较小的数大于的概率为P==.故选:C.12.(3分)已知数列2016,2017,1,﹣2016,﹣2017,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2017项之和等于()A.0 B.2016 C.2017 D.4033【解答】解:设该数列为{a n},从第二项起,每一项都等于它的前后两项之和,=a n+a n+2,即a n+1=a n+1+a n+3,则a n+2两式相加,得a n+a n=0,即a n+3=﹣a n,+3=﹣a n+3=﹣(﹣a n)=a n,∴a n+6∴该数列的周期为6,∵a1+a2+a3+a4+a5+a6=2016+2017+1﹣2016﹣2017﹣1=0,∴S2017=336×(a1+a2+a3+a4+a5+a6)+a1=0+2016=2016.故选:B.二、填空题:本大题共6小题,每小题3分,共l8分将答案填在题中横线上.13.(3分)不等式2x2﹣x≤0的解集为{x|0≤x≤} .【解答】解:不等式2x2﹣x≤0化为x(2x﹣1)≤0,且不等式对应方程的两个实数根为x=0或x=,所以该不等式的解集为{x|0≤x≤}.故答案为:{x|0≤x≤}.14.(3分)某校高一年级三个班共有学生120名,这三个班的男、女生人数如下表.已知在全年级学生中随机抽取1人,抽到二班女生的概率是0.2.则x=24;现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为9.【解答】解:由题意可得=0.2,解得x=24.三班总人数为120﹣20﹣20﹣24﹣20=36,用分层抽样的方法在全年级抽取30名学生,每个学生被抽到的概率为=,故应从三班抽取的人数为36×=9,故答案为24;9.15.(3分)小亮开通了一个微信公众号,每天推送一篇文章,通常将阅读量作为微信公众号受关注度的评判标准,为了提升公众号的关注度,进一步了解大家的需求,小亮对之前推送的100篇文章的阅读量进行了统计,得到如下的频率分布直方图:则图中的a=0.0015.【解答】解:根据频率和为1知,(0.0004+0.0008+2a+0.002+0.0026+0.0006+0.0004+0.0002)×100=1,解得a=0.0015.故答案为:0.0015.16.(3分)当x>0时,不等式x+≥a恒成立,则实数a的取值范围是(﹣∞,2] .【解答】解:当x>0时,不等式x+≥2=2,当且仅当x=1时取等号,∵不等式x+≥a恒成立,∴a≤2,故答案为:(﹣∞,2]17.(3分)已知数列{a n}的前n项和为S n,且a n+S n=1,n∈N*,则a1=;a n=.【解答】解:当n=1时,a1+S1=1,解得a1=,∵a n+S n=1,+S n=1,∴S n﹣S n﹣1﹣1,∴2(S n﹣1)=S n﹣1∵S1﹣1=﹣,∴数列{S n﹣1}是以﹣为首项,以为公比的等比数列,∴S n﹣1=﹣,∴a n=故答案为:,18.(3分)某共享单车公司欲在某社区投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型为运动型,成本为500元/车,骑行半小时需花费0.5元;B型车为轻便型,成本为3000元/车,骑行半小时需花费1元.若公司投入成本资金不能超过10万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时(不足半小时按半小时计算),则在该社区单车公司可获得的总收入最多为120元.【解答】解:根据题意,设投放A型号单车x辆,B型号单车y辆,单车公司可获得的总收入为Z;则有,即,①且Z=2×0.5x+2×y=x+2y,不等式组①表示的平面区域为;分析可得:当x=80,y=20时,Z取得最大值,其最大值Z=80+2×20=120;故答案为:120.三、解答题:本大题共5小题,共46分,解答应写出文字说明、证明过程或演算步骤.19.(7分)如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.(1)求∠ADC的大小;(2)求AB的长.【解答】解:(1)∵AD=5,AC=7,DC=3,∴cos∠ADC==﹣∴∠ADC=120° …(3分)(2)在△ABD中,∠ADB=60°,AD=5,B=45°由正弦定理:,得AB=.…(6分)20.(7分)已知{a n}为等差数列,a1=﹣12,a5=2a6.(I)求数列{a n}的通项公式以及前n项和S n.(Ⅱ)求使得S n>14的最小正整数n的值.【解答】解:(Ⅰ)∵{a n}为等差数列,a1=﹣12,a5=2a6.∴﹣12+4d=2(﹣12+5d),解得d=2,∴a n=﹣12+(n﹣1)×2=2n﹣14.S n==n2﹣13n.(Ⅱ)∵S n>14,∴,且n∈N*,解得n>14,且n∈N*,∴使得S n>14的最小正整数n的值为15.21.(10分)已知sinα﹣2cosα=0.(I)求tan(α+)的值.(Ⅱ)求的值.【解答】解:(I)∵sinα﹣2cosα=0,∴tanα=2,∴tan(α+)===﹣3.(Ⅱ)=2cosα•cosα﹣1=cos2α====﹣.22.(10分)长时间用手机上网严重影响着学生的身体健康,某校为了解A,B 两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.【解答】解:(Ⅰ)A班样本数据的平均值为(9+11+14+20+31)=17,由此估计A班学生每周平均上网时间17小时;B班样本数据的平均值为(11+12+21+25+26)=19,由此估计B班学生每周平均上网时间较长.(Ⅱ)A班的样本数据中不超过21的数据有3个,分别为:9,11,14,B班的样本数据中不超过21的数据也有3个,分别为:11,12,21,从A班和B班的样本数据中各随机抽取一个共有:9种不同情况,分别为:(9,11),(9,12),(9,21),(11,11),(11,12),(11,21),(14,11),(14,12),(14,21),其中a>b的情况有(14,11),(14,12)两种,故a>b的概率P=23.(12分)已知函数f(x),给出如下定义:若f1(x),f2(x),…,f n(x),…(x)),其中均为定义在同一个数集下的函数,且f1(x)=f(x),f n(x)=f(f n﹣1n=2,3,4,…,则称f1(x),f2(x),…,f n(x),…为一个嵌套函数列,记为{f n(x)},若存在非零实数λ,使得嵌套函数列{f n(x)}满足f n(x)=λf n(x),﹣1则称{f n(x)}为类等比函数列.(Ⅰ)已知{f n(x)}是定义在R上的嵌套函数列,若f(x)=+.①求f(2),f2(2),f3(2).②证{f n(x)﹣}是类等比函数列.(Ⅱ)已知{g n(x)}是定义在(1,+∞)上嵌套函数列.若g(x)=(x+),求证|g n(x)﹣g n(x)|<|x﹣|.+1【解答】解:(Ⅰ)若f(x)=+.①则f(2)=,f2(2)=f()=,f3(2)=f()=.②证明:f(x)﹣=,f2(x)﹣=,f3(x)﹣=.…(x)﹣=[f n(x)﹣],猜想:{f n(x)﹣}满足f n﹣1即{f n(x)﹣}是类等比函数列.下面用数学归纳法证明:当n=2时,显然满足条件;假设n=k时,满足条件;则f k(x)﹣=,即f k(x)=,(x)=则f k+1f k+1(x)﹣==,(x)﹣],即f k(x)﹣=[f k+1即n=k+1时,满足条件,故{f n(x)﹣}是类等比函数列.(II)利用数学归纳法证明:|g(x)|=≥=1,当且仅当|x|=1时取等号.依此类推可得:|g n(x)|≥1.(1)当n=1时,g1(x)=(x+),g2(x)=.|g2(x)﹣g1(x)|====×<=.(2)假设n=k∈N*时,|g k+1(x)﹣g k(x)|<.则|g k+2(x)﹣g k+1(x)|==|g k+1(x)﹣g k(x)|•<.∴当n=k+1时也成立,因此|g n+1(x)﹣g n(x)|<|x﹣|.。

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第二学期高一年级阶段数学检测必修第四册学分认定考核试卷说明:本试卷选择题(1-10题)为客观性试题(闭卷30分钟,共40分),填空题与四道大题(11-19题)为主观性试题(开卷60分钟,共60分(其中含卷面书写分5分)),全卷共100分;请将答案写在答题纸的相应位置上.一、选择题:(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案填涂在答题纸上的相应位置)1. 下面四个说法中,正确说法的个数为( )(1)如果两个平面有三个公共点,那么这两个平面重合;(2)两条直线可以确定一个平面;(3)若M a Î,M b Î,l a b =I ,则M l Î;(4)空间中,两两相交的三条直线在同一平面内.A. 1B. 2C. 3D. 4【答案】A【解析】【分析】如果两个平面有三个公共点,那么这两个平面重合或者是相交,即可判断;利用两条异面直线不能确定一个平面即可判断;利用平面的基本性质中的公理3判断即可;若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),即可判断.【详解】如果两个平面有三个公共点,那么这两个平面重合或者是相交,故(1)不正确;两条异面直线不能确定一个平面,故(2)不正确;利用平面的基本性质中的公理3判断(3)正确;空间中,若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),故(4)不正确,综上所述只有一个说法是正确的,故选:A .【点睛】本题主要考查了空间中点,线,面的位置关系.属于较易题.2. 设m 是一条直线,a 、b 是两个不同的平面,则下列命题一定正确的是( )A. 若a b ^,m a ^,则//m bB. 若a b ^,//m a ,则m b^C. 若//a b ,m a ^,则m b^D. 若//a b ,//m a ,则//m b【答案】C【解析】【分析】对于选项A :根据面面垂直的性质定理即可判断;对于选项B :根据面面垂直的性质定理即可判断;对于选项C :根据面面平行的性质定理判断即可;对于选项D :根据线面的位置关系判断即可.【详解】对于选项A :若a b ^,m a ^,则//m b 或m b Ì,故A 不正确;对于选项B :若a b ^,//m a ,则//m b 或m b Ì或m b ^,故B 不正确;对于选项C :若//a b ,m a ^,根据面面平行的性质定理可得m b ^,故C 正确;对于选项D :若//a b ,//m a ,则//m b 或m b Ì,故D 不正确.故选:C.【点睛】本题主要考查了面面垂直的性质定理以及面面平行的性质定理.属于较易题.3. 在ABC V 中,6ABC p Ð=,AB =,3BC =,则AC 等于( )B. 3 D. 21【答案】A【解析】【分析】直接根据余弦定理即可得出结果.【详解】因为6ABC pÐ=,AB =,3BC =,所以2222cos 93233AC BC AB BC AB ABC =+-××Ð=+-´=,即AC =,故选:A.【点睛】本题主要考查了通过余弦定理解三角形,属于基础题.4. 在ABC V 中,根据下列条件解三角形,其中有两个解的是( )A 10b =,45A =°,70C =° B. 60a =,48c =,60B =°C. 8a =,5b =,80A =°D. 13a =,16b =,45A =°【答案】D【解析】【分析】在已知两边及一边对角用正弦定理解三角形时才可能出现两解.根据正弦定理判断.【详解】A :已知两角和一边,三角形确定,只有一解;B :已知两边及夹角用余弦定理,只有一解;C :已知两边及一边对角,但已知的是大边所对的角,小边所对角只能是锐角,不可能有两解;D:sin 16sin 45b A a b =°=<<,有两解.故选:D.【点睛】本题主要考查三角形解的个数问题,掌握正弦定理和余弦定理是解题关键.三角形解的个数中只有在已知两边及一边对角用正弦定理解三角形时才可能出现两解,注意判断方法.属于较易题.5. 若轴截面为正方形的圆柱的侧面积是S ,则圆柱的体积为( )【答案】D【解析】【分析】设出圆柱的高2a ,找到侧面积S 和a 之间的关系,即可求得体积.【详解】根据题意,不妨设圆柱的高为2a ,又因为轴截面为正方形,故可得底面半径为a .则24S a p =,解得a =故可得圆柱体积2224S V a a p p p =´=´=.故选:D.【点睛】本题考查圆柱的侧面积和体积的求解,属基础题.6..把边长为4的正方形ABCD ,沿对角线BD 折成空间四边形ABCD ,使得平面ABD ^平面BCD ,则空间四边形ABCD 的对角线AC 的长为( )A. 4B.C. 2D. 【答案】A【解析】【分析】先利用正方形对角线垂直知对折后AO ^平面BCD 即AO OC ^,在Rt AOC △求AC 即可.【详解】如图所示,正方形ABCD ,对角线交于O 点,则AC BD ^,沿对角线BD 折成空间四边形ABCD 后,有AO BD ^,CO OA ==而平面ABD ^平面BCD ,交线是BD ,故AO ^平面BCD ,即AO OC ^,所以AOC △是等腰直角三角形,故4AC =.故选:A.【点睛】本题考查了面面垂直的性质定理,属于基础题.7. 在ABC V 中,2a =,45B =°,105C =°,则ABC V 的面积是( )A. 2+B.C. 1D. 【答案】C【解析】【分析】利用已知条件先求出A ,在ABC V 中,利用正弦定理求出b ,再利用三角形面积公式求解即可.【详解】由45B =°,105C =°,得30A =°,在ABC V 中,由正弦定理得:2sin sin sin 30sin 45a b b b A B =Þ=Þ=°°则ABC V 的面积是:()11sin 2604522ab C =´´°=°+°60cos 4560sin 451=°°+°°=+,所以ABC V 的面积是1+故选:C.【点睛】本题主要考查了正弦定理以及三角形面积公式,考查了两角和的正弦公式.属于较易题.8.已知过球面上,,A B C 三点的截面和球心的距离等于球半径的一半,且2AB BC CA ===,则球面积是( )A. 169p B. 83p C. 649p D. 4p【答案】C【解析】∵ D 是正△ABC 的中心,∴ AD 是△ABC 的外接圆半径.∵ AD =2sin 60AB =°,又OD =12R =12OA ,OA =OD +AD ,∴ R =21344R + ,∴ R = 649 ,∴ 球的表面积S =4πR =649p .故选C9.如图,在正方体1111ABCD A B C D -中,点P 在面对角线AC 上运动,给出下列四个命题:①1//D P 平面11A BC ;②1D P BD ^;③平面1PDB ^平面11A BC ;④三棱锥11A BPC -的体积不变.则其中所有正确命题的序号是( )A. ①②③B. ②③④C. ①③④D. ①②④【答案】C【解析】【分析】由面面平行的判定与性质判断①正确;由特殊点可以说明②错误;由线面垂直的判定及面面垂直的判定判断③正确;利用等积法说明④正确.【详解】对于①,连接1A B ,11A C ,可得11//AC AC ,11//AB DC ,∴平面11//A BC 平面1ACD ,从而有1//D P 平面11A C B ,故①正确;对于②,连接1111,,D A D B AB ,可知11AD B V 是等边三角形,三角形内角为3p ,所以1D A BD ,所成角为3p,所以当点P 与A 重合时,不满足1D P BD ^,故②错误;对于③,连接1DB ,由111DB A C ^且11DB A B ^,可得1DB ^平面11A C B ,又1DB Ì平面1PDB ,由面面垂直的判定知平面1PDB ^平面11A BC ,故③正确;对于④,容易证明11//A C AC ,从而//AC 平面11A BC ,故AC 上任意一点到平面11A BC 的距离均相等,∴以P 为顶点,平面11A BC 为底面,则三棱锥11A BPC -的体积不变,故④正确.∴正确命题的序号是①③④.故选:C .【点睛】本题考查棱柱的结构特征,考查空间几何元素位置关系的证明,考查三棱锥的体积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.10. 三棱锥V ABC -中,侧面VBC ^底面ABC ,45ABC Ð=°,VA VB =,AC AB =.则( )A. AC BC^ B. VB AC ^ C. VA BC ^ D. VC AB^【答案】C【解析】【分析】由已知条件得到45,ACB AC AB Ð=°^,设BC 的中点为D ,AB 的中点为E ,连接,,,AD VE VD DE ,利用面面垂直性质定理得到AD ^面VBC ,进而得到AD VD ^;再利用线面垂直的判定定理得到AB ^面VDE ,进而得到AB VD ^;最后利用线面垂直的判定定理得到VD ^面ABC ,以D 为坐标原点,DA 为x 轴,DB 为y 轴,DV 为z 轴建立空间坐标系,设,VD b BD DA DC a ====,写出点坐标,利用两个向量的数量积是否为0判断两条线的垂直关系即可.【详解】由AC AB =,45ABC Ð=°,得45,ACB AC AB Ð=°^,故选项A 错误;设BC 的中点为D ,AB 的中点为E ,连接,,,AD VE VD DE ,由题意得:,,//AD BC VE AB DE AC ^^,又面VBC ^面ABC ,且面VBC I 面ABC BC =,AD Ì面ABC ,所以AD ^面VBC ,又VD Ì面VBC所以AD VD ^;//,DE AC AB AC ^,所以DE AB ^,又 VE AB ^,VE DE E =I ,AB Ë面VDE ,则AB ^面VDE ,所以AB VD ^;又AB AD A Ç=,VD Ë面ABC ,所以VD ^面ABC ,则,VD BC VD AD ^^,所以以D 为坐标原点,DA 为x 轴,DB 为y 轴,DV 为z 轴建立空间坐标系,设,VD b BD DA DC a ====,则()()()(),0,0,0,,0,0,,0,0,0,A a B a C a V b -,所以()()(),0,,0,,,0,,VA a b VB a b VC a b =-=-=--uu r uur uuu r ,()()(),,0,,,0,0,2,0AB a a AC a a BC a =-=--=-uuu r uuu r uuu r ,所以220,0,0VA BC VB AC a VC AB a ×=×=-¹×=-¹uu r uuu r uur uuu r uuu r uuu r ,故VA BC ^,选项BD 错误,选项C 正确.故选:C.【点睛】本题主要考查了线面垂直的判定定理以及面面垂直的性质定理,考查了利用空间向量求解两条直线的垂直问题.属于中档题.二、填空题:本大题共5小题,每小题4分,共20分,把答案填在答题纸中相应位置上.11.在ABC V 中,角A ,B ,C 对边分别为a ,b ,c .若222a c b +-=,则角B 的大小为________.【答案】6p 【解析】【分析】利用余弦定理结合已知条件求B 的余弦值即得结果.的【详解】因为222a cb +-=,所以222cos 2ac b B ac +-===又ABC V 中,()0,B p Î,故6B p =,故答案为:6p .【点睛】本题考查了利用余弦定理求角,属于基础题.12. 在ABC V 中,若b =,3c =,30B °=,则a 等于________.【答案】.【解析】【分析】由正弦定理,求得sin C =,得到60C °=或120C °=,分类讨论,即可求得a 的值.【详解】由正弦定理,可得sin sin b c B C =,所以sin sin c B C b ×===,因为(0,180)C Îo o ,所以60C °=或120C °=,当60C °=时,90A °=,可得a ==;当120C °=时,30A °=,此时a b ==,综上可得a =或a =故答案为:.【点睛】本题主要考查了正弦定理的应用,其中解答中利用正弦定理求得sin C 的值,得出C 的大小是解答的关键,着重考查分类讨论,以及运算与求解能力.13.在平地上有A 、B 两点,A 在山的正东,B 在山的东南,且B 在A 的南偏西30°距离A 点300米的地方,在A 测得山顶的仰角是30°,则山高为________米.【答案】150+【解析】【分析】先设山高CD h =,依题意可得ABD Ð,由正弦定理可求得AD ,在直角ADC V 中,tan 30h AD =×°计算得出结果即可.【详解】设山高CD h =,300AB =,()()180180456075ABD ADB DAB Ð=°-Ð+Ð=°-°+°=°,由正弦定理得)sin 1501sin AB ABD AD ADB ×Ð===Ð.在直角ADC V中,)tan 301501150h AD =×°==+.故山高为(150+米.故答案为:150+.【点睛】本题主要考查正弦定理在解三角形中的应用,属于较易题.14. 已知正四棱锥的高为4,侧面积为,则该棱锥的侧棱长为________.【答案】【解析】【分析】由题意画出图形,设正四棱锥的底面边长为a ,由侧面积列式求得a 值,进一步求得侧棱长即可.详解】如图,设正四棱锥P ABCD -的底面边长为a ,底面中心为O ,取BC 的中点M ,【连接OM ,PM ,则2a OM =,斜高PM ==∴该棱锥的侧面积142S a =´´=24a =,又OB =,==,故答案:【点睛】本题考查棱柱的结构特征,考查正四棱锥侧面积的求法,属于基础题.15.如图,在直三棱柱111ABC A B C -中,2BAC pÐ=,11AA AB AC ===,1CC 的中点为H ,点N 在棱11A B 上,//HN 平面1A BC ,则111A N AB 的值为________.【答案】12【解析】【分析】先取111,BB A B 中点,M N 得到过HN 的一个平面平行平面1A BC ,即知11112A N AB =.【详解】取111,BB A B 中点,M N ,连接,HM MN ,为故MH BC P ,1MN A B ∥,又,MH MH 在平面1A BC 外,,BC MN Ì平面1A BC所以MH ∥平面1A BC ,MN ∥平面1A BC ,又,MH MH 相交在平面HMN 内,故平面1A BC P 平面HMN ,即//HN 平面1A BC ,故11112A N AB =.故答案为:12.【点睛】本题考查了面面平行的判定定理,属于基础题.三、解答题:本大题共4小题,共40分.解答应写出文字说明,证明过程或演算步骤.16. 如图,四棱锥P ABCD -中,底面ABCD 为正方形,PA ^平面ABCD ,E 、F 分别是棱PD 、CD 的中点.(1)求证://EF 平面PAC ;(2)求证:EF BD ^.【答案】(1)证明见详解;(2)证明见详解.【解析】【分析】(1)由E 、F 分别是棱PD 、CD 的中点,可得://EF PC ,利用线面平行的判定定理证明即可;(2)利用已知条件得到AC BD ^,PA BD ^,利用线面垂直的判定定理证明BD ^面PAC,所以BD PC ^,又由(1)得//EF PC ,即可得证.【详解】证明:(1)由E 、F 分别是棱PD 、CD 的中点,可得://EF PC ,又EF Ë平面PAC ,PC Ì平面PAC ,所以//EF 平面PAC ;(2)∵底面ABCD 为正方形,AC BD \^,又PA ^平面ABCD ,所以PA BD ^,又PA AC A =I ,BD Ë面PAC ,所以BD ^面PAC ,所以BD PC ^,又由(1)得//EF PC ,所以EF BD ^.【点睛】本题主要考查了线面垂直、线面平行的判定定理,考查了推理能力与空间想象能力,属于较易题.17. 在ABC V 中,1b =,2c =,ABC V.(1)求A Ð;(2)求sin B 的值.【答案】(1)3A p Ð=或23A p Ð=;(2)12.【解析】【分析】(1)根据三角形的面积公式求得sin A 的值,从而可以确定出角A 的大小;(2)由余弦定理求出a ,结合正弦定理可求出sin B 值.【详解】(1)因为1b =,2c =,ABC V所以有121sin 2A ´´´=sin A =,的因为(0,)A p Î,所以3A p Ð=或23A p Ð=;(2)由余弦定理可得:当3A p =时,22212cos 1421232a b c b c A =+-××=+-´´´=,所以a =由正弦定理,sin sin b a B A =,得sin 1sin 2b A B a ===,当23A p =时,22212cos 14212(72a b c b c A =+-××=+-´´´-=,所以a =由正弦定理,sin sin b a B A =,得sin sin b A B a ===,所以sin B 的值为12.【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有三角形的面积公式,余弦定理解三角形,正弦定理解三角形,属于简单题目.18. 在ABC V 中,设内角A ,B ,C 所对的边分别为a ,b ,c,cos sin B b A =.(1)求cos B ;(2)若3c =,AC 边上的中线BD,求边a .【答案】(1)13;(2)1.【解析】【分析】(1)由题中条件,根据正弦定理,先得到sin B B =,代入22sin cos 1B B +=,即可得出结果;(2)根据BD 为AC 边上的中线,得到cos ADB cos DB 0Ð+Ð=C ,根据余弦定理,得出2223AD a =+,再由222cos 2a c b B ac +-=得出22492AD a a =+-,两式联立,即可得出结果.【详解】(1)因为cos sin B b A =,在ABC V 中,由正弦定理可得cos sin sin A B B A =,则sin 0B B =>,所以2222sin cos 8cos cos 1B B B B +=+=,解得1cos 3B =(负值舍去);(2)因为BD 为AC 边上的中线,所以ADB Ð与CDB Ð互补,则cos ADB cos DB 0Ð+Ð=C ,因为BD =,3c =,AD DC =,由余弦定理可得222cos 2AD BD AB ADB AD BD +-Ð==×,222cos 2CD BD BC CDB CD BD +-Ð==×,0=,所以2223AD a =+,又在ABC V 中,22222941cos 263a cb a AD B ac a +-+-===,则22492AD a a =+-,因此226229a a a =+-+,整理得2230a a +-=,解得1a =或3a =-(舍).【点睛】本题主要考查解三角形,熟记正弦定理和余弦定理即可,属于常考题型.19.如图所示,在正方体1111ABCD A B C D -中,点G 在棱11D C 上,且11114D G D C =,点E 、F 、M 分别是棱1AA 、AB 、BC 的中点,P 为线段1B D 上一点,4AB =.(1)若平面EFP 交平面11DCC D 于直线l ,求证:1//l A B ;(2)若直线1B D ^平面EFP ,①求三棱锥1B EFP -的表面积;②试作出平面EGM 与正方体1111ABCD A B C D -各个面的交线,并写出作图步骤,保留作图痕迹设平面EGM 与棱11A D 交于点Q ,求三棱锥Q EFP -的体积.【答案】(1)答案见详解;(2)①6++;②作图步骤见解析,三棱锥Q EFP - 的体积为815.【解析】【分析】(1)根据面面平行的性质即可得到//EF l ,再结合线线平行的传递性即可证明结论;(2)①先根据直线1B D ^平面EFP 得到1B D EP ^,进而得到P 是1DB 的中点,然后依次求出三棱锥的四个面的面积再相加即可得到三棱锥1B EFP -的表面积;②根据公理“一条直线上的两点在一个平面内,那么这条直线在此平面内”作出平面EGM 与正方体1111ABCD A B C D -各个面的交线即可;根据NEFP 四点共面,且三角形PNE 与三角形PEF 面积相等,那么三棱锥Q EFP -的体积等于三棱锥P ENQ -的体积,直接利用三棱锥的体积公式求解即可.【详解】(1)在正方体1111ABCD A B C D -中,因为平面11//ABB A 平面11DCC D ,平面EFP Ç平面11ABB A EF =,所以//EF l ,因为点E 、F 分别是棱1AA 、AB 的中点,所以1//EF A B ,所以1//l A B .(2)①因为直线1B D ^平面EFP ,EP Ì平面EFP ,所以1B D EP ^,又因为DAE D @△11B A E ,所以1DE B E =,所以1DP B P =,因为2EFP S D ==,11122EPB FPB S S D D +=´´=,1162EFB S D =´=,所以三棱锥1B EFP -的表面积为6++②作图步骤如下:连接GE ,过点G 作GH DC ^于点H ,连接HA 并延长交GE 的延长线于点I ,连接IM 并延长交AB 于点J 交DC 的延长线于点K ,再连接GK 交1CC 于点S ,连接MS 并延长交11B C 的延长线于点R ,连接RG 并延长交11A D 于点Q ,再连接EQ ,GS ,EJ ,则图中EQ ,QG ,GS ,SM ,MJ ,JE 即为平面EGM 与正方体各个面的交线.设BJ CK x ==,由题知23AJ HC CK x =+=+,所以1322x AJ HK +==,所以342x x ++=,解得53x =,因为11139553C R C S GC MC SC CK ====,2MC =Q ,\1185C R =,所以111635D Q C R ==,如上图,设N 为线段11A D 的中点,可证点N 在平面PEF 内,且三角形PNE 与三角形PEF 面积相等,所以,三棱锥Q EFP -的体积=三棱锥Q ENP -的体积=三棱锥P ENQ -的体积183215ENQ AB S D ==g ,所以三棱锥Q EFP - 的体积为815.【点睛】本题考查面面平行的性质定理和线面平行的性质定理的应用,直线与平面垂直以及几何体的表面积和体积的求法,考查空间想象能力记忆计算能力,属于难题.。

北京2016—2017学年度第二学期期末考试
高一数学试卷
一、选择题(每小题4分,共32分.在每小题列出的四个选择中,选出符合题目要求的一项,请将答案填在括号里)
1. ).
A. B. C. D.
2. 由观测数据理据有观测数据
,由这两个散点图可以判断().
A. 正相关,
B.
C. D.
3.
所示)).
4. ).
A. B. C. D.
5. 项、第).
A. B. C. D.
6. 下列命题中正确的是().
A. 若两条直线都平行与同一个平面,则这两条直线平行
B. 过一条直线有且只有一个平面与已知平面垂直
C. 若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面
D. 若这两条直线垂直于同一个平面,则这两个直线共面
7. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为().
C.
8. ).
A. B. C. D.
二、填空题(每小题5分,共30分.请将答案填在题中横线上)
9.
__________.
10. __________.
11. 如图在某路段检测点,对
__________.
12.
__________.
13. __________.
14. 为等差比数列,比.现给出下列命题:
①
②等差数列一定是等差比数列;
③,则数列
④若等比数列是等差比数列,则其公比等于公差比.其中正确的命题的序号为__________.。

2016-2017学年北京市中国人民大学附属中学高一下学期期中考试英语试题人大附中2016~2017学年度第二学期高一年级英语期中测试2017年4月26日第二部分:单项填空(共15小题1每小题1分,共15分)21. My dog is cute, smart, and loyal. I couldn?t find a ______ one.A. goodB. betterC. bestD. more better22. It takes three hours to get to the post office, ______ route you take.A. whicheverB. anyC. howeverD. wherever23. What beautiful flowers! And they ______ nice too.A. are smellingB. are smeltC. smeltD. smell24. There are walks of 6-8 hours most days, ______ a maximum of altitude of 5,545 meters.A. inB. forC. atD. with25. If there is anything inconvenient,A. callB. to callC. callingD. called26. Please don?t try to ______ now that everything has been arranged.A. watch outB. back outC. set outD. turn out27. Beijing has become the first city ______ both Summer and Winter Olympic Games after beating Kazakhstan?s Almaty to hold the 2022 Winter Olympics.A. hostedB. hostingC. to hostD. to be hosting28. The number of the books in our school library ______ by 20%.A. has gone upB. is gone upC. are gone upD. have gone up29. She learned some survival skills before, ______ enabled her to go through with the adventure in the Himalayas.A. whichB. thatC. whereD. who30. Silk ______ one of the main goods traded along the SilkRoad by about 100 BC.A. has becomeB. was becomingC. had becomeD. is becoming31. It?s difficult to ______ how exciting bungee jumping is! It?s worth ______ .A. get on, to wait forB. get across, waiting forC. get through, to be waited forD. get down, of waiting for32. Eric the Red was forced to leave Iceland because he had committed a murder, ______ he got into trouble.A. whenB. whichC. whereD. for which33. Once the manager has made a decision, it will be very difficult to persuade him ______ it.A. changeB. changingC. to changeD. to changing34. He has two sons, ______ work as chemists.A. two of whomB. both of whomC. both of whichD. all of whom35. Alex ______ World Cup when someone called him yesterday so he didn?t answer the phone.A. watchedB. will watchC. had watchedD. was watching第三部分:完形填空(共20题,每小题1分,共20分)As a teenager, I was pretty lazy when it came to doing things for my family. I worked hard at school, and sometimes looked after my younger sister. Still, I found myself regularly resisting the urge to 36 out at home with even the simplest things.Every Wednesday afternoon, for example, my mother 37 me to another town for a piano lesson. During my two-hour lesson, she?d rush to the nearby store and buy a week?s worth of 38 . Given the fact that my mom had driven me twelve miles there, twelve miles back, 39 for my lesson, and bought me a candy bar, you?d think I?d be very 40 to help her bring the groceries into the house. 41 I wasn?t. I generally just brought in an armload and left the 42 for Mom as I ran to my room, shut the door, and started studying.Don?t get me wrong: even back in my room, I felt 43 about not helping my mother more. Deep inside, I wanted to change my 44 . But I also realized that once I did change, there?d be no going back. 45 I took on more responsibility, my parents would start 46 more of me. At age fifteen, I sensed that this one small change would 47 something much bigger: my personal change from a cared-for, spoiled (被宠坏的)child to a more 48 , caring and giving young man.I?ll never forget the Wednesday when I made a(n)49 to jump in and see what happened. Returning home from the 50 , I disappeared into my room, as usual. But once inside, I felt that deep and burning 51 . Throwing my school books on the bed, Isuddenly opened my door and 52 back to the garage to help my mother. How happy I felt that day!Surely, over time, I continued to help out with more housework. The neat thing was, the more I helped out, the 53 I felt about myself and my place in my family. As Mom and Dad realized they could 54 on me more, our trips became far less stressful, too. In short, it was a win-win situation for everyone.Sometimes the little things we put off doing the longest 55 out to be the simplest things to complete. And feeling happy beats feeling guilty any day.36. A. help B. handle C. start D. work37. A. transported B. walked C. drove D. guided38. A. fruits B. groceries C. flowers D. vegetables39. A. paid B. fought C. applied D. planned40. A. nervous B. grateful C. confident D. unwilling41. A. So B. And C. Thus D. But42. A. one B. other C. next D. rest43. A. anxious B. guilty C. curious D. doubtful44. A. ambition B. aim C. way D. shape45. A. Since B. Though C. Unless D. Once46. A. expecting B. banning C. warming D. informing47. A. differ B. mark C. tell D. educate48. A. energetic B. ambitious C. responsible D. outgoing49. A. dictation B. decision C. statement D. appointment50. A. duty B. store C. lesson D. holiday51. A. anger B. shame C. delight D. excitement52. A. called B. looked C. headed D. handed53. A. better B. smarter C. warmer D. stronger54. A. live B. press C. focus D. count55. A. bring B. make C. point D. turn第四部分:阅读理解(共16题,每题2分,共32分)AA newly discovered ancient Chinese map may prove that it was a Chinese navigator who first discovered America. He may have made the discovery seventy years before Columbus discovered the New World.The map, which has gone on display in Beijing, is said to be a copy made in 1763 of a much older map dating back to 1418. It clearly describes Africa, Europe and the Americas. If it's proven to be believable, the map would provide strong evidence to suggest that the famous Ming Dynasty sailor, Zheng He, beat Christopher Columbus, who arrived in America in 1492, to the discovery of the New World.Liu Gang, a Chinese lawyer and map collector, bought the map in an antique store in Shanghai in 2001 for about 500 U.S. dollars. Liu Gang thinks the map supports the thesis of British author, Gavin Menzies, who in his 2003 book argued Zheng He was the first person to circumnavigate(环航)the globe and discover America sometime between 1421 and 1423. “In principle, the British author Gavin is right. Before Columbus, Zheng He discovered America and the whole world. But in detail, not exactly... three years difference. I don?t think that?s a big deal. ” Liu said.Zheng He commanded a group of ships, which sailed between 1405 and 1433 at the order of the emperor during China?s Ming Dynasty. His aim was to spread the glory of China to the world and establish trade.56. We learn from Paragraph 1 that ______ .A. the writer was proud of an ancient mapB. both the Chinese navigator and Columbus were heroesC. the ancient map made by a Chinese navigator was just foundD. the Chinese navigator may be the first man who discovered America57. Which of the following correctly describes the ancient map?A. The ancient map on display in Beijing is said to be made in 1418.B. The ancient map, which is said to be made in 1763, is on display in Beijing.C. The ancient map was bought by Liu Gang, a Chinese navigator in 2001.D. The ancient map was introduced to be listed in Gavin? book by Liu Gang to support his idea.58. What does the British author in his book try to argue in the passage?A. The first person who discovered America may be Zheng He.B. The first person to circumnavigate the globe is not worth discussing.C. The year when Zheng He discovered America may be between 1421 and 1423.D. The year when Christopher Columbus discovered America was ahead of 1423.59. Which of the following would be the best title for the passage?A. Ancient Map and Liu Gang.B. Zheng He, Liu Gang and British Author.C. Zheng He Spreads the Glory of China to the World.D. Ancient Map Suggests Chinese Discovered America.BThere is a lot of talk these days about how kids should be interested in science. Here?s an area of science for everyone, and these cool new books might inspire you to discover your inner。
北京市东城区2016-2017学年高一(下)期末数学试卷一、选择题1.(3分)某同学参加期末模拟考试,考后对自己的语文和数学成绩进行了如下估计:语文成绩(x)高于85分,数学成绩(y)不低于80分,用不等式组可以表示为()A.B.C.D.2.(3分)在数列{a n}中,a n+1=a n+1,n∈N*,则数列的通项可以是()A.a n=﹣n+1 B.a n=n+1 C.a n=2n D.a n=n23.(3分)sin43°cos17°+cos43°sin17°的值为()A.B.C.D.14.(3分)在等差数列{a n}中,已知a3=2,a5+a8=15,则a10=()A.64 B.26 C.18 D.135.(3分)执行如图所示的程序框图,则输出的s值为()A.﹣ B.C.2 D.36.(3分)现有八个数,它们能构成一个以1为首项.﹣3为公比的等比数列,若从这八个数中随机抽取一个数,则它大于8的概率是()A.B.C.D.7.(3分)若不等式m<n与<(m,n为实数)同时成立,则()A.m<n<0 B.0<m<n C.m<0<n D.mn>08.(3分)欲测量河宽即河岸之间的距离(河的两岸可视为平行),受地理条件和测量工具的限制,采用如下办法:如图所示,在河的一岸边选取A,B两个观测点,观察对岸的点C,测得∠CAB=75°,∠CBA=45°,AB=120米,由此可得河宽约为(精确到1米,参考数据≈2.45,sin75°≈0.97)()A.170米B.110米C.95米D.80米9.(3分)已知{a n}为等比数列,S n为其前n项和.a3﹣a1=15,a2﹣a1=5,则S4=()A.75 B.80 C.155 D.16010.(3分)甲、乙、丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图所示若s甲,s乙,s丙分别表示他制测试成绩的标准差,则它们的大小关系为()A.S丙<S甲<S乙B.S甲<S丙<S乙C.S乙<S丙<S甲D.S丙<S乙<S甲11.(3分)若在区间[0,2]中随机地取两个数,则这两个数中较小的数大于的概率是()A.B.C.D.12.(3分)已知数列2016,2017,1,﹣2016,﹣2017,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2017项之和等于()A.0 B.2016 C.2017 D.4033二、填空题13.(3分)不等式2x2﹣x≤0的解集为.14.(3分)某校高一年级三个班共有学生120名,这三个班的男、女生人数如下表.已知在全年级学生中随机抽取1人,抽到二班女生的概率是0.2.则x=;现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为.15.(3分)小亮开通了一个微信公众号,每天推送一篇文章,通常将阅读量作为微信公众号受关注度的评判标准,为了提升公众号的关注度,进一步了解大家的需求,小亮对之前推送的100篇文章的阅读量进行了统计,得到如下的频率分布直方图:则图中的a=.16.(3分)当x>0时,不等式x+≥a恒成立,则实数a的取值范围是.17.(3分)已知数列{a n}的前n项和为S n,且a n+S n=1,n∈N*,则a1=;a n=.18.(3分)某共享单车公司欲在某社区投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型为运动型,成本为500元/车,骑行半小时需花费0.5元;B型车为轻便型,成本为3000元/车,骑行半小时需花费1元.若公司投入成本资金不能超过10万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时(不足半小时按半小时计算),则在该社区单车公司可获得的总收入最多为元.三、解答题19.(7分)如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.(1)求∠ADC的大小;(2)求AB的长.20.(7分)已知{a n}为等差数列,a1=﹣12,a5=2a6.(I)求数列{a n}的通项公式以及前n项和S n.(Ⅱ)求使得S n>14的最小正整数n的值.21.(10分)已知sinα﹣2cosα=0.(I)求tan(α+)的值.(Ⅱ)求的值.22.(10分)长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.23.(12分)已知函数f(x),给出如下定义:若f1(x),f2(x),…,f n(x),…均为定义在同一个数集下的函数,且f1(x)=f(x),f n(x)=f(f n﹣1(x)),其中n=2,3,4,…,则称f1(x),f2(x),…,f n(x),…为一个嵌套函数列,记为{f n(x)},若存在非零实数λ,使得嵌套函数列{f n(x)}满足f n﹣1(x)=λf n(x),则称{f n(x)}为类等比函数列.(Ⅰ)已知{f n(x)}是定义在R上的嵌套函数列,若f(x)=+.①求f(2),f2(2),f3(2).②证{f n(x)﹣}是类等比函数列.(Ⅱ)已知{g n(x)}是定义在(1,+∞)上嵌套函数列.若g(x)=(x+),求证|g n+1(x)﹣g n(x)|<|x﹣|.【参考答案】一、选择题1.A【解析】∵语文成绩(x)高于85分,数学成绩(y)不低于80分,∴,故选:A.2.B【解析】∵a n+1=a n+1,n∈N*,∴a n+1﹣a n=1,n∈N*,∴数列{a n}为公差为1的等差数列,其中A,a n=﹣n+1中,a n+1﹣a n=﹣(n+1)+1+n﹣1=﹣1,不满足,B,a n=n+1中,a n+1﹣a n=(n+1)+1+n﹣1=1,满足,C:为等比数列,不满足,D:a n+1﹣a n=(n+1)2﹣n2=2n+1,不满足,故选:B.3.C【解析】sin43°cos17°+cos43°sin17°=sin(43°+17°)=sin60°=,故选:C.4.D【解析】设公差为d,a3=2,a5+a8=15,∴a3+2d+a3+5d=15,解得7d=11,∴a10=a3+7d=2+11=13,故选:D.5.D【解析】i=0<4,s=3,i=1<4,s=,i=2,s=﹣,i=3<4,s=3,i=4≥4,输出s=3,故选:D.6.D【解析】由题意成等比数列的8个数为:1,﹣3,(﹣3)2,(﹣3)3…(﹣3)7;其中大于8的项有:(﹣3)2,(﹣3)4,(﹣3)6,共3个数这8个数中随机抽取一个数,则它大于8的概率是P=;故选D.7.C【解析】∵m<n与<(m,n为实数)同时成立,∴只有mn<0时,=<0.∴m<0<n.故选:C.8.C【解析】在△ABC中,∠ACB=180°﹣75°﹣45°=60°,由正弦定理得:,∴AC===40,∴S△ABC=AB•AC•sin∠CAB=≈5703.6,∴C到AB的距离d==≈95.故选C.9.A【解析】∵a3﹣a1=15,a2﹣a1=5,由等比数列的通项,可得a1q2﹣a1=15,a1q﹣a1=5,∵a2﹣a1≠0,∴q≠1解得:a1=5,q=2.那么:S4=a1+a2+a3+a4==75.故选:A.10.A【解析】甲的平均成绩为(7+8+9+10)×0.25=8.5,其方差为S甲2=0.25×[(7﹣8.5)2+(8﹣8.5)2+(9﹣8.5)2+(10﹣8.5)2]=1.25乙的平均成绩为7×0.3+8×0.2+9×0.2+10×0.3=8.5,其方差为S乙2=0.3×(7﹣8.5)2+0.2×(8﹣8.5)2+0.2×(9﹣8.5)2+0.3×(10﹣8.5)2=1.45 丙的平均成绩为7×0.2+8×0.3+9×0.3+10×0.2=8.5,其方差为S丙2=0.2×(7﹣8.5)2+0.3×(8﹣8.5)2+0.3×(9﹣8.5)2+0.2×(10﹣8.5)2=1.05 ∴S丙2<S甲2<S乙2∴S丙<S甲<S乙.故选:A.11.C【解析】在区间[0,2]中随机地取一个数,这两个数中较小的数大于的概率为P==.故选:C.12.B【解析】设该数列为{a n},从第二项起,每一项都等于它的前后两项之和,即a n+1=a n+a n+2,则a n+2=a n+1+a n+3,两式相加,得a n+3+a n=0,即a n+3=﹣a n,∴a n+6=﹣a n+3=﹣(﹣a n)=a n,∴该数列的周期为6,∵a1+a2+a3+a4+a5+a6=2016+2017+1﹣2016﹣2017﹣1=0,∴S2017=336×(a1+a2+a3+a4+a5+a6)+a1=0+2016=2016.故选:B.二、填空题13.{x|0≤x≤}【解析】不等式2x2﹣x≤0化为x(2x﹣1)≤0,且不等式对应方程的两个实数根为x=0或x=,所以该不等式的解集为{x|0≤x≤}.故答案为:{x|0≤x≤}.14.249【解析】由题意可得=0.2,解得x=24.三班总人数为120﹣20﹣20﹣24﹣20=36,用分层抽样的方法在全年级抽取30名学生,每个学生被抽到的概率为=,故应从三班抽取的人数为36×=9,故答案为24;9.15.0.0015【解析】根据频率和为1知,(0.0004+0.0008+2a+0.002+0.0026+0.0006+0.0004+0.0002)×100=1,解得a=0.0015.故答案为:0.0015.16.(﹣∞,2]【解析】当x>0时,不等式x+≥2=2,当且仅当x=1时取等号,∵不等式x+≥a恒成立,∴a≤2,故答案为:(﹣∞,2]17.【解析】当n=1时,a1+S1=1,解得a1=,∵a n+S n=1,∴S n﹣S n﹣1+S n=1,∴2(S n﹣1)=S n﹣1﹣1,∵S1﹣1=﹣,∴数列{S n﹣1}是以﹣为首项,以为公比的等比数列,∴S n﹣1=﹣,∴a n=故答案为:,18.120【解析】根据题意,设投放A型号单车x辆,B型号单车y辆,单车公司可获得的总收入为Z;则有,即,①且Z=2×0.5x+2×y=x+2y,不等式组①表示的平面区域为;分析可得:当x=80,y=20时,Z取得最大值,其最大值Z=80+2×20=120;故答案为:120.三、解答题19.解:(1)∵AD=5,AC=7,DC=3,∴cos∠ADC==﹣∴∠ADC=120°(2)在△ABD中,∠ADB=60°,AD=5,B=45°由正弦定理:,得AB=.20.解:(Ⅰ)∵{a n}为等差数列,a1=﹣12,a5=2a6.∴﹣12+4d=2(﹣12+5d),解得d=2,∴a n=﹣12+(n﹣1)×2=2n﹣14.S n==n2﹣13n.(Ⅱ)∵S n>14,∴,且n∈N*,解得n>14,且n∈N*,∴使得S n>14的最小正整数n的值为15.21.解:(I)∵sinα﹣2cosα=0,∴tanα=2,∴tan(α+)===﹣3.(Ⅱ)=2cosα•cosα﹣1=cos2α====﹣.22.解:(Ⅰ)A班样本数据的平均值为(9+11+14+20+31)=17,由此估计A班学生每周平均上网时间17小时;B班样本数据的平均值为(11+12+21+25+26)=19,由此估计B班学生每周平均上网时间较长.(Ⅱ)A班的样本数据中不超过21的数据有3个,分别为:9,11,14,B班的样本数据中不超过21的数据也有3个,分别为:11,12,21,从A班和B班的样本数据中各随机抽取一个共有:9种不同情况,分别为:(9,11),(9,12),(9,21),(11,11),(11,12),(11,21),(14,11),(14,12),(14,21),其中a>b的情况有(14,11),(14,12)两种,故a>b的概率P=23.(Ⅰ)①解:若f(x)=+.则f(2)=,f2(2)=f()=,f3(2)=f()=.②证明:f(x)﹣=,f2(x)﹣=,f3(x)﹣=.…猜想:{f n(x)﹣}满足f n﹣1(x)﹣=[f n(x)﹣],即{f n(x)﹣}是类等比函数列.下面用数学归纳法证明:当n=2时,显然满足条件;假设n=k时,满足条件;则f k(x)﹣=,即f k(x)=,则f k+1(x)=f k+1(x)﹣==,即f k(x)﹣=[f k+1(x)﹣],即n=k+1时,满足条件,故{f n(x)﹣}是类等比函数列.(II)证明:利用数学归纳法证明:|g(x)|=≥=1,当且仅当|x|=1时取等号.依此类推可得:|g n(x)|≥1.(1)当n=1时,g1(x)=(x+),g2(x)=.|g2(x)﹣g1(x)|====×<=.(2)假设n=k∈N*时,|g k+1(x)﹣g k(x)|<.则|g k+2(x)﹣g k+1(x)|==|g k+1(x)﹣g k(x)|•<.∴当n=k+1时也成立,因此|g n+1(x)﹣g n(x)|<|x﹣|.。
大附中朝阳学校2016—2017学年期中试题高一数学试卷(时间120分钟满分100分)一、选择题(本题包括8小题,每小题4分,共计32分。
每小题只有一个选项符合题意。
)1. 已知集合,,则集合( )。
A。
B. C。
D.【答案】A【解析】∵集合,,由并集的定义可得:,本题选择A选项.2。
下列函数在其定义域内既是奇函数又是增函数的是(). A。
B。
C. D。
【答案】D【解析】选项,,定义域是,它在定义域上单调递增,但是是非奇非偶函数,故错误;选项:,它在定义域上单调递增,是非奇非偶函数,故错误;选项:,定义域是,是奇函数,有两个单调减区间;和,但在整个定义域上不单调,故错误;选项:,是奇函数,当时,,在上是增函数,所以在上是增函数,故正确.本题选择D选项.3。
为了得到函数的图象,只需把函数上所有点()。
A。
向右平移个单位长度,再向下平移个单位长度B。
向左平移个单位长度,再向下平移个单位长度C. 向右平移个单位长度,再向上平移个单位长度D. 向左平移个单位长度,再向上平移个单位长度【答案】A【解析】函数图象的平移问题:在x上的变化符合“左加右减",而在y上的变化符合“上加下减”.把函数y=2x的图象向右平移3个单位长度得到函数y=2x﹣3的图象,再将所得图象再向下平移1个单位长度,得到函数y=2x﹣3﹣1的图象故选A4. 下列函数中,表示同一个函数的是().A. 与B. 与C. 与D。
与【答案】C【解析】选项,,定义域是,定义域是,两个函数的定义域不同;所以不表示同一个函数,故错;选项,,,两个函数的对应法则不同,所以不表示同一个函数;故错;选项,,定义域是,,定义域是,两个函数定义域和对应法则都相同,所以表示同一个函数,故正确;选项,定义域是,定义域是,两个函数的定义域不同,所以不表示同一个函数,故错误.本题选择C选项.点睛:判断两个函数是否为相同函数.一是定义域是否相同,二是对应关系即解析式是否相同(注意解析式可以等价化简).5. 函数的零点所在的一个区间是().A。
北京市中国人民大学附属中学2016-2017学年高一下学期期中考试数学试题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、单选题1.在ABC V 中,若1cos 3A =,则cos()B C +=( ) A .13B .13-C .3D .3-2.设,,a b R a b ∈>,则下列不等式一定成立的是( ) A .22a b > B .11a b< C .2a ab > D .22a b > 3.在等差数列{}n a 中,12a =,543a a =+,那么3a =( ) A .5B .8C .9D .144.等比数列{}n a 的公比为2,则3412a a a a --的值为( )A .14B .12C .4D .25.函数1()(2)2f x x xx =+>-最小值是() A .1B .2C .3D .46.已知A 船在灯塔C 北偏东70°方向2km 处,B 船在灯塔C 北偏西50°方向3km 处,则A ,B 两船的距离为( ) ABC .1)kmD .1)km7.若,x y 满足1021010x y x y x y ++≥⎧⎪+-≤⎨⎪-+≤⎩,则下列不等式恒成立的是( )A .0x ≥B .1y ≥C .210x y -+≤D .210x y ++≤8.甲、乙两企业每年缴纳的地税逐年增加,并且甲企业的年增长数相同,乙企业的年增长率相同.若这两家企业在2003年和2009年所缴地税分别相同,则它们在2015年企业缴纳地税的情况是( ) A .甲多B .乙多C .一样多D .不能确定9.若等比数列{}n a 的前n 项和()321nn S =-,则22212n a a a ++⋅⋅⋅+=( )A .413n -B .41n -C .()341n-D .()941n-10.如图,已知A 、B 、C 、D 四点在同一条直线上,在山顶P 点测得点A 、C 、D 的俯角分别为30︒、60︒、45︒,并测得200AB m =,100CD m =,现欲沿直线AD 开通穿山隧道,则隧道BC 的长为( )A.1)m B.1)m + C. D.11.学校为了奖励评选出来的15名“校园科技小小发明家”,设置了一、二、三等奖: ①一等奖1000元/名,二等奖600元/名,三等奖400元/名,奖金总额不超过9000元; ②一等奖人数不得超过二等奖人数,二等奖人数不得超过三等奖人数. 则三等奖的奖金总额最少为( ) A .2400元 B .3000元C .6000元D .6600元第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题12.不等式23100x x --<解集是__________.13.已知等差数列{}n a 的前n 项和为n S ,若735S =,则35a a +=________. 14.若△ABC 中,sinA:sinB:sinC 2:3:4=,那么cosC= 。
2016-2017北京高一下期末
一、选择题:(每题有且只有一个答案,每题5分,共60分)
1. ).
A. B. C. D.
2. 的夹角的大小为().
A. B. C. D.
3. 如图所示,在放置的四个几何体中,其正视图为矩形的是().
A. B. C. D.
4. 中,角).
A. B.
C. D.
5. 是等差数列,且).
6. 设,,且,则().
A. B. C. D.
7. ,平面).
A. B.
C. D.
8. ,,,,,,则角().
9. 已知某几何体的三视图(单位:).
10. 设向量,满足:,,以,,的模为边长构成三角形,则它的边与半径为圆的公共点个数最多为().
A. B. C. D.
11.
错误
..的为().
A. B.
C. D.
12. ).
B. D.
二、填空题:(每题5分,共6×5=30分)
13. __________.
14. .
15. 的最小值为__________.
16. 中,____________________.
17. ,
确的是__________.(请把正确答案的题号写在横线上)
三、解答题:
18. 的大小.
19. 古希腊人常用小石子在沙滩上摆成各种形状来研究数,他们把以下形状的数成为三角形数(如图).
______).(请将正确答案的选项填在括号内)
A B C D
是其前
①项的和
②
20.
21. 的边长为,,沿对角线
.
22. ,且满足。