当前位置：文档之家 › 高三物理复习：动量定理在流体模型中的应用 课件

高三物理复习：动量定理在流体模型中的应用 课件

  • 格式：pptx
  • 大小：1.09 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

动量定理的应用-完整PPT课件

动量定理的应用-完整PPT课件


自动称米机是准确的，不存在谁划算不划算的问题 设米流的流量为 d( kg/ s ),它是恒定的，自动装置能即刻在出口处切断米流，米流在出口处速度很小，
可视为零，若切断米流后，盛米容器中静止的那部分米的质量为 m 1,空中还在下落的米的质量为 m 2, 则落到已静止的米堆 m 1 上的一部分米的质量为Δ m 取Δ m 为研究对象，这部分米很少，在Δ t 时间内 Δ m ＝ d ·Δ t ,设其落到米堆上之前的速度为 v ,经Δ t 时间静止，其受力如右图所示，由动量定理得 （ F -Δ mg ）Δ t =Δ mv 1, 即 F =d v +d·Δ t · g 设米从出口处落到米表面所用的时间为 t 1 ,由于 m 2=d·t 1 v = g ·t 1 (阻力不计) 可得d·v = m 2·g , 即 F = m 2g +Δ mg , 根据牛顿第三定律知： F = F ′, 称米机的读数应为
v
mgt v0ts
mg
v0s
பைடு நூலகம்
110 3
0.32 10 10 0.5104
m
/
s
6.4m /
s
故 h v2 v02 6.42 10 2 m 2.97m
2g 2 (10)
从喷嘴向上喷出的水柱从下到上，横截面积越来越大。由于 液体不能压缩，所以通过整个水柱每个横截面的流量相等。
练习3.为估算池中睡莲叶面承受液滴撞击产生的 平均压强,小明在雨天将一圆柱形水杯置于露台, 测得1小时内杯中水上升了45 mm.查询得知,当时 雨滴竖直下落速度约为12 m/s.据此估算该压强约 为(设雨滴撞击睡莲后无反弹,不计雨滴重力,雨水 的密度为1×103 kg/m3)
解析：规定水反射回来的速度方向为正方向，取Δt时间内
动量定理在流体问题上的应用.pptx

动量定理在流体问题上的应用.pptx


vt
陨石的质量为：
S
m Svt
由动量定理得：
Ft m v
F Sv2
由牛顿第三定律，飞船 所受阻力：
F F Sv2 因此推力 F推 Sv2
例三、一艘帆船在静水中由于风力的推动做匀速直线运 动，帆面的面积为S，风速为v1，船速为v2（v2﹤v1）， 空气密度为ρ，帆船在匀速前进时帆面受到的平均风力 大小为多少？（设空气碰到帆后随帆一起运动）
F

F1

F2

3m 2L
g 2t 2
当： t 2L g
F 3mg
动量定理在流体问题 上的应用
精品文档
例一、高压采煤水枪出水口的截面积为S，水的射速为
v，射到煤层上后，水速度为零，若水的密度为ρ，求
水对煤层的冲力。
Δt时间内冲到煤层上的
水的体积为
V Svt 这些水的质量为：
m Svt
由动量定理得：
vt
S
Ft m0 v
F Sv2
由牛顿第三定律，水对 煤层的冲力为：
F F Sv2
例二、最大截面S＝5m2的一艘宇宙飞船，以速度v＝
10km/s在太空中航行时，进入静止的、密度ρ＝2×10－5
kg/m3的微陨石云中。如果微陨石与飞船相撞时都附着
在飞船上，要使飞船维微
例四、一质量为m，长为L的柔软绳自由悬垂，下端恰 与一台秤秤盘接触。某时刻放开柔软绳上端，求台秤的 最大示数。（重力加速度大小为g）
0—t时间内静止在台秤上的 绳子的长度为
L1

1 2
gt
2
质量为：
m1

m
L1 L
对台秤的压力为：
动量定理高三复习课件ppt

动量定理高三复习课件ppt

是一面墙,如图所示。物块以v0=9 m/s的初速度从A点
沿AB方向运动,在与墙壁碰撞前瞬间的速度为7 m/s,
碰后以6 m/s的速度反向运动直至静止。g取 10 m/s2。
(1)求物块与地面间的动摩擦因数μ;
(2)若碰撞时间为0.05 s,求碰撞过程中墙面对物块平均作用力的大小F;
(3)求物块在反向运动过程中克服摩擦力所做的功W。
)
图2
A．I＝0
B．I＝mv0
C．I＝2mv0
D．I＝3mv0
知识梳理·双基过关
课堂互动·研透考点
@《创新设计》
1 2 1 2
解析 设木块离开弹簧时的速度为 v，根据机械能守恒定律得： mv ＝ mv0，所
2
2
以 v＝v0，设向右的速度方向为正方向，根据动量定理得：I＝mv－(－mv0)＝2mv0，
W＝－2 J
D．Δp＝－0.4 kg·m/s
W＝2 J
@《创新设计》
动量的变化量（初、末动量不在同一直线上）
2．[应用动量定理求动量的变化量]如图 1 所示，跳水运动员从
某一峭壁上水平跳出，跳入湖水中，已知运动员的质量 m＝
70 kg，初速度 v0＝5 m/s，若经过 1 s 时，速度为 v＝5 5 m/s，
，
g
sin θ
m 2gh
方向竖直向下，故选项 A 错误；斜面弹力的冲量大小为 IN＝mgcos θ·
t＝
，方向垂直
tan θ
斜面向上，选项 B 正确，C 错误；合力的大小为 mgsin θ，I 合＝mgsin θ·
t＝m 2gh，方向沿
斜面向下(与合力方向相同)，即合力冲量的大小相同，方向不同，故选项 D 正确。
高中物理模型：应用动量定理解决流体模型的冲击力问题

高中物理模型：应用动量定理解决流体模型的冲击力问题

模型/题型：应用动量定理处理“流体模型”的冲击力问题一、模型概述1.研究对象：常常需要选取流体为研究对象，如水、空气等.2.研究方法：隔离出一定形状的一部分流体作为研究对象，然后列式求解.3.基本思路(1)在极短时间Δt 内，取一小柱体作为研究对象. (2)求小柱体的体积ΔV ＝vS Δt(3)求小柱体质量Δm ＝ρΔV ＝ρvS Δt(4)求小柱体的动量变化Δp ＝v Δm ＝ρv 2S Δt (5)应用动量定理F Δt ＝Δp二、题型分类处理办法 模型一流体类问题通常液体流、气体流等被广义地视为“流体”，质量具有连续性，通常已知密度ρ建立“柱状”模型，沿流速v 的方向选取一段柱形流体，其横截面积为S模型二 微粒类问题 三、典型例题1.(2016·全国卷Ⅰ·35(2))某游乐园入口旁有一喷泉，喷出的水柱将一质量为M 的卡通玩具稳定地悬停在空中.为计算方便起见，假设水柱从横截面积为S 的喷口持续以速度v 0竖直向上喷出；玩具底部为平板(面积略大于S )；水柱冲击到玩具底板后，在竖直方向水的速度变为零，在水平方向朝四周均匀散开.忽略空气阻力.已知水的密度为ρ，重力加速度大小为g .求：(1)喷泉单位时间内喷出的水的质量；(2)玩具在空中悬停时，其底面相对于喷口的高度.答案 (1)ρv 0S (2)v 022g － M 2g2ρ2v 02S2解析 (1)在刚喷出一段很短的Δt 时间内，可认为喷出的水柱保持速度v 0不变. 该时间内，喷出水柱高度Δl ＝v 0Δt① 喷出水柱质量Δm ＝ρΔV ② 其中ΔV 为水柱体积，满足ΔV ＝ΔlS ③由①②③可得：喷泉单位时间内喷出的水的质量为 ΔmΔt＝ρv 0S (2)设玩具底板相对于喷口的高度为h 由玩具受力平衡得F 冲＝Mg④ 其中，F 冲为水柱对玩具底板的作用力 由牛顿第三定律：F 压＝F 冲⑤ 其中，F 压为玩具底板对水柱的作用力，设v ′为水柱到达玩具底面时的速度由运动学公式：v ′2－v 02＝－2gh ⑥ 在很短Δt 时间内，冲击玩具的水柱的质量为Δm Δm ＝ρv 0S Δt⑦ 由题意可知，在竖直方向上，对该部分水柱应用动量定理 (F 压＋Δmg )Δt ＝Δmv ′ ⑧ 由于Δt 很小，Δmg 也很小，可以忽略，⑧式变为 F 压Δt ＝Δmv ′⑨由④⑤⑥⑦⑨可得h ＝v 022g －M 2g 2ρ2v 02S22.如图所示，由喷泉中喷出的水柱，把一个质量为M 的垃圾桶倒顶在空中，水以速率v0、恒定的质量增率(即单位时间喷出的质量)ΔmΔt从地下射向空中.求垃圾桶可停留的最大高度.(设水柱喷到桶底后以相同的速率反弹)答案 h ＝v 022g －M 2g 8(Δt Δm)2解析 设垃圾桶可停留的最大高度为h ，并设水柱到达h 高处的速度为vt ，则 v 2－v 02＝－2gh得v 2＝v 02－2gh由动量定理得，在极短时间Δt 内，水受到的冲量为FΔt＝2(ΔmΔt ·Δt)v解得F ＝2Δm Δt ·vt＝2Δm Δtv 02－2gh据题意有F ＝Mg联立解得h ＝v 022g －M 2g 8(Δt Δm)23. 有一宇宙飞船，它的正面面积S = 0.98m2，以v = 2×103 m/s 的速度飞入一宇宙微粒尘区，此尘区每立方米空间有一个微粒，微粒的平均质量m = 2×10﹣7 kg ，要使飞船速度保持不变，飞船的牵引力应增加多少？（设微粒与飞船外壳碰撞后附于飞船上）。

动量定理的应用PPT

动量定理的应用PPT


(2)注意分离后两物体运动性质的分析;
(说的流体包括:气体、液体、流沙及 基本粒子流等. 这类问题的特点是:研究对象是不断变化着 的.所以,分析这类问题时要特别注意研究对 象的选择.常用的方法是“微元”法.




例题5.一艘帆船在静水中行驶,由于风力的作用做 匀速直线运动,帆面的面积S=10m2,风速 V1=10m/s,船速V2=4m/s,空气的密度 ρ=1.29kg/m3.帆船受到的平均风力多大? 解析:取一小段时间t,并以在这段 (V1-V2)t 时间内与帆面作用的空气为研究 对象. 这部分空气的质量为:ρS(V1-V2)t, 其速度由V1变V2,根据动量定理得: Ft= ρS(V1-V2)2t 解得:F=464.4N

例题3.物块A和B用轻绳相连后悬在弹簧下端静止不动如 图所示.连接A、B的绳子断裂后,A上升到某位置时速度的 大小为V,这时B下落的速度大小为μ,已知A、B的质量分别 为m和M,则在这段时间里,弹簧弹力对A的冲量为 . 解析:从问题出发,对过程进行分析. 过程中A受重力和弹力作用,设时间为t, 则根据动量定理得: IA+mgt=mV…………① 对B应用动量定理得: Mgt=Mμ…………② 解方程组得:IA=m(μ+V)
A B






解:分离后A做竖直上抛运动,由运动规律得: VA0=(2gh)1/2=2m/s t=VA0/g=0.2s B做简谐运动,机械能守恒.因此,B再经弹簧原长处 的速度大小仍为VA0.对B应用动量定理(以向下为 正) IB+mBgt=2mBVA0 代入已知条件及相关量解得:IB=6N· s 点拨:(1)注意应用分离状态时两物体间的关联关系;
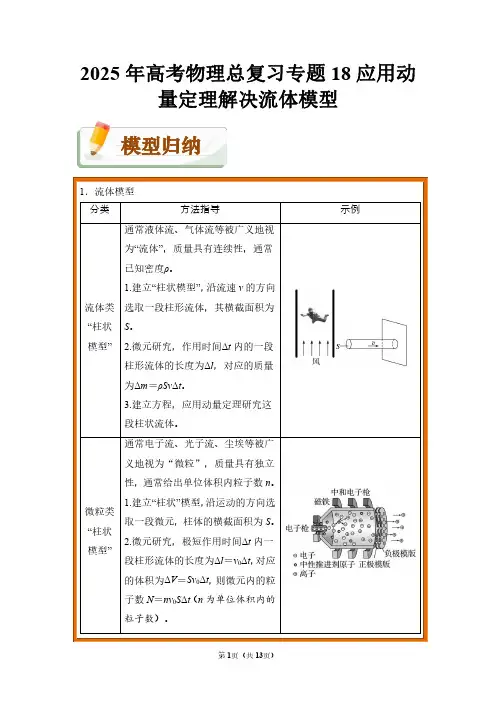
2025年高考物理总复习专题18 应用动量定理解决流体模型(附答案解析)

2025年高考物理总复习专题18 应用动量定理解决流体模型(附答案解析)

第1页（共13页）2025年高考物理总复习专题18应用动量定理解决流体模型模型归纳
1．流体模型
分类方法指导
示例
流体类“柱状
模型”通常液体流、气体流等被广义地视
为“流体”，质量具有连续性，通常
已知密度ρ。

1.建立“柱状模型”，沿流速v 的方向
选取一段柱形流体，其横截面积为S 。

2.微元研究，作用时间Δt 内的一段
柱形流体的长度为Δl ，对应的质量
为Δm ＝ρSv Δt 。

3.建立方程，应用动量定理研究这
段柱状流体。

微粒类
“柱状
模型”通常电子流、光子流、尘埃等被广
义地视为“微粒”，质量具有独立
性，通常给出单位体积内粒子数n 。

1.建立“柱状”模型，沿运动的方向选取一段微元，柱体的横截面积为S 。

2.微元研究，极短作用时间Δt 内一段柱形流体的长度为Δl ＝v 0Δt ，对应
的体积为ΔV ＝Sv 0Δt ，则微元内的粒
子数N ＝nv 0S Δt （n 为单位体积内的
粒子数）。

高中物理选择性必修一《动量定理解流体问题》教学课件

高中物理选择性必修一《动量定理解流体问题》教学课件


05.
例题精选
例题3
（2021·湖北·高考真题）抗日战争时期，我军缴获不少敌军武器武装自己，
其中某轻机枪子弹弹头质量约8 g，出膛速度大小约750 m/s。某战士在使用
该机枪连续射击1分钟的过程中，机枪所受子弹的平均反冲力大小约12 N，
则机枪在这1分钟内射出子弹的数量约为（
A．40
B．80
C．120
感谢观看
ห้องสมุดไป่ตู้
高中物理选择性必修第一册
第一章：专题1
动量定理解流体问题
目录
模型建构
题型突破
第一部分
模型建构
01. 流体模型
流体及
通常液体流、气体流等被广义地视为“流体”，质量具有连续性，通常已知密度ρ
其特点
分
析
步
骤
v
1
建立“柱状模型”，沿流速v的方向取一段柱形流体，其横截面积为S
2
微元研究，作用时间Δt内的一段柱形流体的长度为Δl，对应的质量为Δm＝ρSvΔt
1
0 2
2
1
2
+ 0 ℎ = 0 0 2 ，在ℎ高度处，Δ时间内喷射到玩具底面的水沿竖直
方向的动量变化量的大小为Δ = 0 ，设水对玩具的作用力的大小为F，根据
动量定理有Δ = Δ，由于玩具在空中悬停，由力的平衡条件得 = ，联
立式得ℎ =
02
2
−
2
22 02 2
2.反弹型：作用后流体微元以速率v反弹
有Δv＝－2v，代入上式有F＝－2ρSv2。
第二部分
题型突破
01.
例题精选
例题1
（2019·全国·高考真题）最近，我国为“长征九号”研制的大推力新型火箭发
动量定理及其应用课件

动量定理及其应用课件


VS
量子力学中的动量定理
将动量定理应用于量子力学领域，研究其 在描述微观粒子运动和相互作用中的作用 。
动量定理在交叉学科领域的研究
工程力学中的动量定理
将动量定理应用于工程力学领域，研究其在 结构分析、振动控制等方面的应用。
生物学中的动量定理
将动量定理应用于生物学领域，探讨其在描 述生物运动、生态平衡等方面的作用。
棒球投手投球
棒球投手通过改变球的速度和角度来 控制球的轨迹。这需要运用动量定理 来预测球在空中的运动轨迹，以便投 手能够准确地将球投到目标位置。
滑雪技巧
在滑雪过程中，运动员通过改变滑行 速度和方向来控制自己的轨迹。这需 要运用动量定理来理解速度和方向变 化对滑雪轨迹的影响。
工业生产中的应用
机械加工
全。
军事科技
导弹和炮弹的制导和射击精度也 依赖于动量定理来计算和控制弹 道轨迹，提高武器的打击效果。
04 动量定理的实验验证
实验设计
01
02
03
实验目标
验证动量定理在现实生活 中的应用，探究物体在碰 撞过程中的动量变化。
实验原理
基于动量定理，当一个物 体发生碰撞时，其动量的 变化与作用力和作用时间 的乘积成正比。
对碰撞问题的解决
动量定理为解决碰撞问题提供了重要 的工具，使得科学家能够预测和解释 物体碰撞过程中的各种现象。
动量定理在现代科技领域的应用
火箭科学
火箭发动机的推进原理正是基于 动量定理，通过高速喷射物质来 获得反作用力，从而实现火箭的
升空和推进。
碰撞安全研究
汽车、飞机和其他交通工具的碰 撞安全研究依赖于动量定理来分 析碰撞过程中能量的传递和吸收 ，以改进安全设计和保护乘员安
动量定理的应用课件

动量定理的应用课件


REPORTING
安全气囊的工作原理
安全气囊
安全气囊是汽车安全系统的重要组成部分，它能够在车辆碰撞时迅速充气膨胀， 为乘员提供保护。
应用动量定理
当车辆发生碰撞时，安全气囊中的气体发生器迅速释放大量气体，使气囊迅速膨 胀。由于气体的动量定理（pΔt=mΔv），气体的快速膨胀导致气囊对乘员产生 一个反向的冲击力，以减缓乘员的前冲速度，从而降低伤害风险。
火箭飞行问题中，利用动量定理可以计算 火箭喷气速度和推力之间的关系，以及火 箭起飞时的质量变化。
应用实例
解题思路
一个火箭以恒定速度喷气，求火箭起飞时 的推力和质量。
利用动量定理，可以求出火箭起飞时的推 力和质量，判断火箭是否能够起飞。
投掷问题
总结词
动量定理在投掷问题中也有广 泛应用，可以计算投掷物体的
应用实例
一个球以速度v撞向静止的球，求碰撞后两球的速度。
详细描述
在碰撞问题中，动量定理可以用来计算碰撞前后的动量变 化，从而判断碰撞是弹性碰撞还是非弹性碰撞，以及碰撞 后物体的运动状态。
解题思路
利用动量定理，可以求出碰撞后两球的速度，判断是否满 足动量守恒定律。
火箭飞行问题
总结词
详细描述
动量定理在火箭飞行问题中具有重要应用 ，可以计算火箭的推力和质量之间的关系 。
详细描述
动量定理是指物体动量的变化量等于 作用力与时间的乘积，即Ft=Δp，其 中F表示作用力，t表示作用时间，Δp 表示动量的变化量。
动量定理的物理意义
总结词
动量定理揭示了力对时间的累积效应，即力在一段时间内对物体动量的影响。
详细描述
动量定理表明，一个恒力在一段时间内对物体产生持续作用，将会引起物体动 量的相应变化。动量定理适用于任何惯性参考系中，描述的是物体动量的变化 与作用力之间的关系。
动量和动量定理—(人教版)高考大一轮复习优质课件ppt

动量和动量定理—(人教版)高考大一轮复习优质课件ppt


化量为(g＝10 m/s2，不计空气阻力)( )
A.700 kg·m/s C.350( 5－1) kg·m/s
B.350 5 kg·m/s D.350( 5＋1) kg·m/s
解析：运动员只受重力， 则由动量定理可知动 量的变化量为 Δp＝mgt ＝70×10×1 kg·m/s ＝ 700 kg·m/s，故 A 正确， B、C、D 错误。
动量和动量定理—（人教版）高考大 一轮复 习优质 课件ppt
返回
动量和动量定理—（人教版）高考大 一轮复 习优质 课件ppt
考点二 动量定理的理解和应用
解析：物体质量为 0.1 kg，即重力为 1 N，在 0～1 s 时间内物体保持静止，即物体是从 1 s 后开始向上加速运动的，A 错误； F－mg 在第 3 s 末物体所受拉力最大，a＝ m ＝20 m/s2，a>g，此时加速度最大，B 正确； 根据 IF＝Ft 可知，图线与坐标轴围成的面积表示 F 的冲量，所以 5～9 s 内 F 与重力 的冲量之和为零，则动量变化量为零，即第 5 s 末和第 9 s 末物体的速度相等，C 正 确； 物体在 0～9 s 所受 F 与重力的冲量之和 I 总＝F2mt－mgt＝4.5 N·s，方向向上，则第 9 s 末物体的速度方向向上且不为零，物体没有上升到最高点，D 错误。
2.动量定理的应用技巧 (1)应用 I＝Δp 求变力的冲量 如果物体受到大小或方向改变的力的作用，则不能直接用 I＝Ft 求冲量，可以求 出该力作用下物体动量的变化 Δp，等效代换得出变力的冲量 I。 (2)应用 Δp＝FΔt 求动量的变化 例如，在曲线运动中，速度方向时刻在变化，求动量变化(Δp＝p2－p1)需要应用 矢量运算方法，计算比较复杂。如果作用力是恒力，可以求恒力的冲量，等效代 换得出动量的变化。
高考物理复习：动量定理及应用精品课件

高考物理复习：动量定理及应用精品课件


(2)动量定理中的冲量是 合力 的冲量，而不是某一个力的冲量，它可以 是合力的冲量，可以是各力冲量的矢量和，也可以是外力在不同阶段冲 量的矢量和. (3)动量定理表达式是矢量式，等号包含了大小相等、方向相同两方面的 含义.
自测2 (多选)质量为m的物体以初速度v0开始做平抛运动，经过时间t， 下降的高度为h，速度变为v，在这段时间内物体动量变化量的大小为
√A.动能相等，则质量大的动量大
B.动能相等，则动量大小也相等
√C.动量大小相等，则质量大的动能小
D.动量大小相等，则动能也相等
答案
例2 (2018·甘肃西峰调研)如图2所示，竖直面内有一个固定圆环，MN 是它在竖直方向上的直径.两根光滑滑轨MP、QN的端点都在圆周上， MP>QN.将两个完全相同的小滑块a、b分别从M、Q点无初速度释放，在 它们各自沿MP、QN运动到圆周上的过程中，下列说法中正确的是 A.合力对两滑块的冲量大小相同 B.重力对a滑块的冲量较大
C.甲的动能增加量一定等于乙的动能减少量
D.甲对乙做多少负功，乙对甲就一定做多少正功
图1
答案

变式1 (多选)两个质量不同的物体，如果它们的
√A.动能相等，则质量大的动量大
B.动能相等，则动量大小也相等
√C.动量大小相等，则质量大的动能小
D.动量大小相等，则动能也相等
答案
变式1 (多选)两个质量不同的物体，如果它们的
第六章 动量 动量守恒定律
第1讲 动量定理及应用
内容索引
过好双基关
回扣基础知识 训练基础题目
研透命题点
细研考纲和真题 分析突破命题点
课时作业
限时训练 练规范 练速度
过好双基关
一、动量、动量变化、冲量 1.动量 (1)定义：物体的 质量 与 速度 的乘积. (2)表达式：p＝ mv . (3)方向：动量的方向与 速度 的方向相同. 2.动量的变化 (1)因为动量是矢量，动量的变化量Δp也是 矢量 ，其方向与速度的改变 量Δv的方向 相同 . (2)动量的变化量Δp的大小，一般用末动量p′减去初动量p进行计算，也 称为动量的增量.即Δp＝ p′－p .

动量定理中的流体模型(解析版)--2025届高考物理热点模型

动量定理中的流体模型学校：_________班级：___________姓名：_____________模型概述1.研究对象1)流体类：液体流、气体流等，通常已知密度ρ2)微粒类：电子流、光子流、尘埃等，通常给出单位体积内粒子数n微粒类先应用动量定理研究单个粒子,建立方程,再乘N计算2.处理方法1)构建“柱状”模型：沿流速v的方向选取一小段柱体，其横截面积为S2)微元研究①小段柱体的体积ΔV=vSΔt②小段柱体质量m=ρΔV=ρvSΔt③小段柱体粒子数N=nvSΔt④小段柱体动量p=mv=ρv2SΔt3)列出方程，应用动量定理FΔt=Δp研究典题攻破1.应用动量定理处理流体模型1.(2024·甘肃平凉·模拟预测)2023年10月31日，神舟十六号载人飞船返回舱在东风着陆场成功着陆。

如图所示，距离地面高度约1m时，返回舱底部配备的4台着陆反推发动机开始点火竖直向下喷气，喷出的燃气相对于喷气前返回舱的速度为v，4台发动机喷气口的横截面积均为S，喷出燃气的密度为ρ。

喷出的气体所受重力忽略不计。

反推发动机工作时燃气对返回舱作用力的大小为()A.4ρSv2B.ρSv2C.4ρSvD.ρSv【答案】A【详解】极短的时间Δt内喷出的燃气质量Δm=ρvΔt⋅4S=4ρvΔtS根据动量定理有FΔt=Δmv联立解得F=4ρSv2由牛顿第三定律知反推发动机工作时燃气对返回舱作用力的大小为F =F=4ρSv2故选A。

【典型题2】(2024·上海黄浦·二模)消防员用横截面积为S的喷水枪，喷出恒定流速为v的水流，水流垂直射向着火的墙体后，速度可视为0。

水的密度为ρ，水流的重力忽略不计。

求：(1)水枪在Δt时间内喷出水的质量。

(2)墙体受到水流平均冲击力的大小。

【答案】(1)Δm=ρSvΔt；(2)ρSv2【详解】(1)水枪在Δt时间内喷出水的质量为Δm=ρSvΔt(2)以水喷出的方向为正方向，与墙体碰撞过程中Δt时间内的水，根据动量定理得-FΔt=0-Δmv解得F=ρSv2根据牛顿第三定律可得，墙体受到水流平均冲击力的大小F =F=ρSv2针对训练1.(2024·河北邢台·二模)某同学利用身边的常见器材在家完成了有趣的物理实验，如图所示。

高三物理复习：动量定理在流体模型中的应用 课件

动量定理在流体模型中的应用
• 某游乐园入口旁有一喷泉,喷出的水柱将一 质量为M的卡通玩具稳定地悬停在空中。 为计算方便起见，假设水柱从横截面积为S 的 底喷 部口为持平续板以（速 面度 积略v0竖大直于向S ）上；喷水出柱；冲玩击具到 玩具底板后，在竖直方向水的速度变为零， 在水平方向朝四周均匀散开。忽略空气阻 力。已知水的密度为 ρ，重力加速度大小为 g ，求：
• （2）物理思想：认为外界的作用只对进出该 空间的流体产生效果
• （3）质量关系：流进该区域的质量等于流出 该区域的质量∆m进=∆m出
• （4）研究对象：∆t→0时间流入（或流出）该 区域的流体∆m。∆m=ρsv∆t
• （5）力学关系：外界对该区域的总冲量等于进、
出流体动量变化
• （1）画模型，取研究对象 选∆t时间内附着在飞船上的尘埃，这部分尘 埃长v∆t，横截面积为S
S
v∆t
• （2）写出研究对象的质量∆m：∆m=ρSv∆t • （3）画受力，选好初、末态：
v0=0
vt=v
S
F
S
F
v∆t
• 初态：静止不动
末态：以速度v和飞船一起运动
• （4）运用动量定理求作用力：
• F∆t=∆m v-0
• F∆t=ρSv∆t v-0
• F=ρSv2
• 带入数据得：F=20N
• 2、研究∆t时间内转移的质量：适合一切稳定 流体
• （1）稳定流体的特点：流体在空间上的分布 不随时间变化，即部分稳定的流体的质量、电 量、能量和动量等均不变
• （2）物理思想：认为外界的作用只对进出该 空间的流体产生效果
• （1）模型：处理截面积为S，长为v∆t的小柱体 （可以是圆柱体也可以是长方体）

动量定理在流体问题上的应用ppt课件

击到玩具底板后，在竖直方向水的速度变为零，在水平 方向朝四周均匀散开。忽略空气阻力。已知水的密度为ρ， 重力加速度大小为g，求： (i) 喷泉单位时间内喷出的水的质量； (ii) 玩具在空中悬停时，其底面相对于喷口的高度。完整最新ppt8 Nhomakorabeavt
陨石的质量为：
S
m Svt
由动量定理得：
Ft m v
F Sv2
由牛顿第三定律，飞船 所受阻力：
F F Sv2 因此推力 完整最新ppt
F推
Sv2 3
例三、一艘帆船在静水中由于风力的推动做匀速直线运 动，帆面的面积为S，风速为v1，船速为v2（v2﹤v1）， 空气密度为ρ，帆船在匀速前进时帆面受到的平均风力 大小为多少？（设空气碰到帆后随帆一起运动）
完整最新ppt
5
0—t时间内静止在台秤上的 绳子的长度为
L1
1 2
gt 2
质量为：
m1
m
L1 L
对台秤的压力为：
F1
m L
1 2
gt 2
t—t+Δt时间内撞击台秤的 绳子速度为
v gt
t—t+Δt时间内撞击台秤的 绳子质量为
m m vt L
对这些绳子用动量定理：
mg FN t m0 v
其中： mg FN 忽略不计
v1 v2 t
S
这些空气的质量为：
m Sv1 v2 t
对这些空气由动量定理得：
v1
v2
Ft mv2 v1
Δt时间内吹到帆面上的 空气体积为
得： F Sv1 v2 2
由牛顿第三定律，帆受 到的风力
V Sv1 v2 t
F F
完整最新ppt
S
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• （2）物理思想：认为外界的作用只对进出该 空间的流体产生效果
• （3）质量关系：流进该区域的质量等于流出 该区域的质量∆m进=∆m出
• （4）研究对象：∆t→0时间流入（或流出）该 区域的流体∆m。∆m=ρsv∆t
• （5）力学关系：外界对该区域的总冲量等于进、
出流体动量变化
• （1）画模型，取研究对象 选∆t时间内附着在飞船上的尘埃，这部分尘 埃长v∆t，横截面积为S
S
v∆t
• （2）写出研究对象的质量∆m：∆m=ρSv∆t • （3）画受力，选好初、末态：
v0=0
vt=v
S
F
S
F
v∆t
• 初态：静止不动
末态：以速度v和飞船一起运动
• （4）运用动量定理求作用力：
• F∆t=∆m v-0
• (i)喷泉单位时间内喷出的水的质量；
• (ii)玩具在空中悬停时，其底面相对于喷口 的高度。
知识回顾
• 1、动量定理: 物体所受合外力的冲量等于物体
的动量变化，这就是动量定理。
Ft mv' mv I p
• 2、动量定理的应用步骤： • （1）确定研究对象：一般为单个物体； • （2）明确物理过程：受力分析，求出合外力
• 2、写出研究对象的质量∆m：∆m=ρhLv∆t
• 3、画受力，选好初、末态
L
L
h
h
F
F
初态：v0=v
末态：vt=0
• 4、运用动量定理求作用力 • 规定以原速度方向为正方向 • -F∆t=0-∆m v • F∆t=ρhLv∆t v • F=ρhLv2
• 例2：有一宇宙飞船以v=10 km/s的速度在太 空中飞行，突然进入一密度为ρ=10-7kg/m3 的微陨石尘区，假设微陨石与飞船碰撞后 即附着在飞船上．欲使飞船保持原速度不 变，试求飞船的助推器的助推力应增大为 多少？（已知飞船的横截面积S=2 m2）
• F∆t=ρSv∆t v-0
• F=ρSv2
• 带入数据得：F=20N
• 2、研究∆t时间内转移的质量：适合一切稳定 流体
• （1）稳定流体的特点：流体在空间上的分布 不随时间变化，即部分稳定的流体的质量、电 量、能量和动量等均不变
• （2）物理思想：认为外界的作用只对进出该 空间的流体产生效果
• （3）质量关系：流进该区域的质量等于流出 该区域的质量∆m进=∆m出
• （4）研究对象：∆t→0时间流入（或流出）该 区域的流体∆m。∆m=ρsv∆t
• （5）力学关系：外界对该区域的总冲量等于进、
出流体动量变化
• 某游乐园入口旁有一喷泉,喷出的水柱将一质 量为M的卡通玩具稳定地悬停在空中。为计 算方便起见，假设水柱从横截面积为S 的喷 口平持板续（以面速积度略大v0竖于直S ）向；上水喷柱出冲；击玩到具玩底具部底为 板后，在竖直方向水的速度变为零，在水平 方向朝四周均匀散开。忽略空气阻力。已知 水的密度为 ρ，重力加速度大小为g ，求：
S
S
v∆t v∆t
• （2）∆m的计算：∆m=ρsv∆t
• （3）作用过程：由∆例1：飓风以速度v推进，空 气密度为ρ，防风墙高为h， 长为L，风遇到防风墙后速 度变为零，且只考虑风对防
风墙的作用，试求风对防风 墙的冲击力。
• 解：1、画模型，取研究对象 L h
动量定理在流体模型中的应用
• 某游乐园入口旁有一喷泉,喷出的水柱将一 质量为M的卡通玩具稳定地悬停在空中。 为计算方便起见，假设水柱从横截面积为S 的 底喷 部口为持平续板以（速 面度 积略v0竖大直于向S ）上；喷水出柱；冲玩击具到 玩具底板后，在竖直方向水的速度变为零， 在水平方向朝四周均匀散开。忽略空气阻 力。已知水的密度为 ρ，重力加速度大小为 g ，求：
• （1）模型：处理截面积为S，长为v∆t的小柱体 （可以是圆柱体也可以是长方体）
• （2）∆m的计算：∆m=ρsv∆t • （3）作用过程：由∆t很小，∆m很小，可看成物块与物体的碰撞
• 2、研究∆t时间内转移的质量：适合一切稳定 流体
• （1）稳定流体的特点：流体在空间上的分布 不随时间变化，即部分稳定的流体的质量、电 量、能量和动量等均不变
的冲量； • （3）明确研究对象的初末状态及相应的动量； • （4）选定正方向，确定在物理过程中研究对
象的动量的变化； • （5）根据动量定理列方程，统一单位后代入
数据求解。
• 1、研究∆t→0时间内参与作用的流体：适用 于流体运动过程中局部发生速度突变问题
• （1）模型：处理截面积为S，长为v∆t的小柱 体（可以是圆柱体也可以是长方体）
• (i)喷泉单位时间内喷出的水的质量；
• (ii)玩具在空中悬停时，其底面相对于喷口的 高度。
S1
v
h
v0 S
易错点：
S1
1、用喷口处截面积时， v
∆m=ρSv0∆t
h
2、用玩具处截面积时，
∆m=ρS1v∆t
v0 S
课堂小结
• 1、研究∆t→0时间内参与作用的流体：适用于流体运动过程中局部发生 速度突变问题