动量定理手写笔记

动量知识点总结课堂笔记一、动量的概念1. 动量的定义动量是描述物体运动状态的物理量，是物体质量和速度的乘积。

在经典力学中，动量通常用p来表示，其大小为动量的大小与速度的大小的乘积，方向与速度方向一致。

2. 动量的公式物体的动量p可以用以下公式表示：p = mv其中，p为物体的动量，m为物体的质量，v为物体的速度。

3. 动量的性质a. 动量是矢量，有大小和方向。

b. 动量与速度成正比，与质量成正比。

c. 动量守恒定律：在封闭系统内，系统的总动量保持不变。

二、动量定理1. 动量定理的表述在牛顿力学中，动量定理可以用以下公式表示：FΔt = Δp其中，F为作用力，Δt为作用时间，Δp为动量的改变量。

2. 动量定理的含义动量定理表明：在作用力作用下，物体的动量发生改变，动量的改变量等于作用力乘以作用时间。

3. 动量定理的应用动量定理可以用来分析物体在外界作用力下的运动状态，以及描述物体在碰撞过程中动量的转移和转换。

三、动量守恒定律1. 动量守恒定律的表述在一个封闭系统内，当外部作用力为零时，系统的总动量保持不变，即总动量守恒。

2. 动量守恒定律的应用动量守恒定律可以用来分析碰撞过程中动量的转移和转换，从而推导碰撞前后物体的速度和动量的关系。

3. 动量守恒定律的实际意义动量守恒定律描述了物体在碰撞过程中动能的转化情况，可以帮助我们理解和预测物体碰撞后的运动状态。

四、碰撞1. 碰撞的分类a. 完全弹性碰撞：碰撞后物体的动能保持不变。

b. 完全非弹性碰撞：碰撞后物体会发生形变，动能会损失。

c. 部分弹性碰撞：碰撞后既发生形变，又有部分动能损失。

2. 碰撞中的动量转移和转换在碰撞过程中，物体的动量会相互转移和转换，根据动量守恒定律，我们可以通过动量守恒关系推导物体碰撞后的速度和动量。

3. 碰撞的实际应用碰撞理论在交通工程、材料研究、工程设计等领域有着广泛的应用，可以用来分析和改进碰撞安全性能，提高材料的抗碰撞性能等。

龙文教育动量知识点总结一、对冲量的理解1、I =Ft ：适用于计算恒力或平均力F 的冲量，变力的冲量常用动量定理求。

2、I 合 的求法：A 、若物体受到的各个力作用的时间相同，且都为恒力，则I 合=F 合.tB 、若不同阶段受力不同，则I 合为各个阶段冲量的矢量和。

1、意义：冲量反映力对物体在一段时间上的积累作用，动量反映了物体的运动状态。

2、矢量性：ΔP 的方向由v ∆决定，与1p 、2p 无必然的联系，计算时先规定正方向。

三、对动量守恒定律的理解：1、研究对象：相互作用的物体所组成的系统2、条件： A 、理想条件：系统不受外力或所受外力有合力为零。

B 、近似条件：系统内力远大于外力，则系统动量近似守恒。

C 、单方向守恒：系统单方向满足上述条件，则该方向系统动量守恒。

结论：等质量 弹性正碰 时，两者速度交换。

依据：动量守恒、动能守恒五、判断碰撞结果是否可能的方法：碰撞前后系统动量守恒；系统的动能不增加；速度符合物理情景。

动能和动量的关系：mp E K 22= K mE p 2=六、反冲运动：1、定义：静止或运动的物体通过分离出一部分物体，使另一部分向反方向运动的现象叫反冲运动。

2、规律：系统动量守恒3、人船模型：条件：当组成系统的2个物体相互作用前静止，相互作用过程中满足动量守恒。

七、临界条件：“最”字类临界条件如压缩到最短、相距最近、上升到最高点等的处理关键是——系统各组成部分具有共同的速度v。

八、动力学规律的选择依据：1、题目涉及时间t，优先选择动量定理；2、题目涉及物体间相互作用，则将发生相互作用的物体看成系统，优先考虑动量守恒；3、题目涉及位移s，优先考虑动能定理、机械能守恒定律、能量转化和守恒定律；4、题目涉及运动的细节、加速度a，则选择牛顿运动定律+运动学规律；九、表达规范：说明清楚研究对象、研究过程、规律、规定正方向。

典型练习一、基本概念的理解：动量、冲量、动量的改变量1、若一个物体的动量发生了改变，则物体的（）A、速度大小一定变了B、速度方向一定变了C、速度一定发生了改变D、加速度一定不为02、质量为m的物体从光滑固定斜面顶端静止下滑到底端，所用的时间为t, 斜面倾角为θ。

动量定理·知识点精解1．冲量的概念(1)冲量是描述力在某段时间内累积效应的物理量，是描写过程的物理量。

(2)力的冲量是矢量对于具有恒定方向的力来说，冲量的方向与力的方向一致；对于作用时间内方向变化的力来说，冲量的方向与相应时间内物体动量改变量的方向一致。

冲量的运算应使用平行四边形法则。

如果物体所受合外力的冲量都在同一条直线上，那么选定正方向后，冲量的方向可以用正、负号表示，冲量的运算就简化为代数运算了。

(3)冲量的计算若物体受到大小、方向都不变的恒力作用，力的冲量的数值等于力与作用时间的乘积，冲量的方向与恒力方向一致；若力为同一方向均匀变化的力，该力的冲量可以用平均力计算；若力为一般变力则不能直接计算冲量。

(4)冲量的绝对性由于力与时间均与参考系无关，所以力的冲量也与参考系的选择无关。

2．冲量的公式由冲量的定义知，冲量用I 表示，力F在时间t内的冲量可以表示为：I＝F·t3．冲量的单位(1)冲量单位由力和时间单位决定，在国际单位制中，冲量单位是：牛顿·秒。

(2)冲量的单位1牛·秒=1秒·千克·米/秒2＝1千克·米/秒，同动量变化量的单位相同，但在使用过程中，两者的单位不能混用，注意区别。

4．动量定理(1)物体所受合外力的冲量，等于这个物体动量的增加量，这就是动量定理。

设质量为m的物体受恒定合外力F的作用，在Δt时间内，速度由v1变为v2，其动量的改变为ΔP＝mv2-mv1，合外力F的冲量为I=FΔt，又因F=ma，a=(v2-v1)/Δt联立得：FΔt＝ma·Δt＝mv2-mv1＝ΔP。

(2)动量定理的研究对象是单个物体或可视为单个物体的系统。

当研究对象为物体系时，物体系总动量的增量等于相应时间内物体系所受的合外力的冲量。

所谓物体系总动量的增量是指系统内各物体的动量变化量的矢量和。

所谓物体系所受的合外力的冲量是指系统内各物体所受的一切外力的冲量的矢量和，而不包括系统内部物体之间的相互作用力(内力)的冲量；这是因为内力总是成对出现的，而且它们的大小相等、方向相反，其矢量和总等于零。

动量定理定律一、动量定理应用的误区警示1．应用Δ求变力的冲量I p如果物体受到大小或方向改变的力的作用,则不能直接用I=Ft求变力的冲量，可以求出该力作用下物体动量的变化Δp，等效代换变力的冲量I。

2．应用Δ=Δp F t求动量的变化在曲线运动中，速度方向时刻在变化,求动量变化需要应用矢量运算方法，计算较复杂.若作用力为恒力，可求恒力冲量，等效代换动量的变化。

二、动量守恒定律成立条件的误区1．系统不受外力或系统所受外力的矢量和为零，则系统动量守恒。

2．系统所受合外力虽不为零，但系统的内力远大于外力，如碰撞、爆炸等现象中，系统的动量可近似看作守恒.3．系统所受合外力虽然不为零，如果在某一个方向上合外力为零，那么在该方向上动量守恒。

三、碰撞类问题的易错点1．忽视了动量守恒的条件，在系统所受合外力不为零的情况下仍用动量守恒求解；2．不理解动量守恒定律的矢量性，按代数和的方法求和动量；3．在动量守恒定律的表达式中，速度选取了不同的参考系;4．忽视了碰撞过程中的机械能损失.从同样高度静止落下的玻璃杯，掉在水泥地上容易打碎，而掉在草地上不容易打碎,其原因是A．掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小B．掉在水泥地上的玻璃杯动量改变大，掉在草地上的玻璃杯动量改变小C．掉在水泥地上的玻璃杯动量改变快，掉在草地上的玻璃杯动量改变慢D．掉在水泥地上的玻璃杯与地面接触时，相互作用力小，而掉在草地上的玻璃杯受地面的冲击力大【错因分析】本题较易出错的理解是掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小，认为打碎的原因是动量大。

【正确解析】从同样高度静止落下的玻璃杯，掉在水泥地上和掉在草地上速度相同，动量相同，故A错误；玻璃杯掉在水泥和掉在草地上初动量相同,末动量都为零,所以动量变化量相同；故B 错误；掉在水泥地上的玻璃杯与水泥作用时间短，动量变化量一定，动量改变快，掉在草地上的玻璃杯与草地作用时间长，动量变化量一定,动量改变慢，故C 正确；由动量定理()0F mg t mv -=-可得mv F mg t=-+ 掉在水泥地上的玻璃杯与地面接触时，相互作用力大，而掉在草地上的玻璃杯受地面的冲击力小,故D 错误。

动量守恒定律和能量守恒定律笔记在学习物理的旅程中，动量守恒定律和能量守恒定律就像是两座神秘而又威严的城堡，等待着我去探索和征服。

先来说说动量守恒定律吧。

有一次，我和小伙伴在操场上玩弹珠。

那一颗颗晶莹剔透的弹珠，在阳光下闪烁着迷人的光芒。

我们规定，谁把对方的弹珠弹出界外，谁就赢了。

当时我就发现了一个有趣的现象，当我的弹珠用力地撞向对方静止的弹珠时，我的弹珠速度减慢了，而对方的弹珠却飞速地向前冲去。

这其实就是动量守恒定律在起作用！原本我的弹珠具有一定的动量，在碰撞的瞬间，一部分动量传递给了对方的弹珠，所以两者的总动量在碰撞前后并没有发生改变。

为了更清楚地理解这个定律，我还特意做了一个小实验。

我找来了两个小车，一个重一些，一个轻一些。

在光滑的平面上，让重的小车以一定的速度向前行驶，然后让轻的小车从后面追上去并碰撞。

碰撞的那一瞬间，重车的速度明显减慢，轻车的速度则加快了不少。

这就好比两个武林高手过招，内力在他们之间传递，总内力却不变。

再讲讲能量守恒定律。

记得有一次，我骑自行车下坡。

那坡可真陡啊！一开始，我得用力蹬脚踏板才能爬上坡顶，累得气喘吁吁。

可当我到达坡顶，准备下坡的时候，那种感觉简直太棒了！我根本不需要用力蹬，自行车就风驰电掣般地向下冲去。

而且速度越来越快，耳边的风声呼呼作响。

这时候我就在想，上坡的时候我付出了很多的能量，累得要命。

而下坡的时候，这些能量似乎又都回来了，转化成了自行车的动能和势能。

就好像我在银行存了一笔钱，上坡时我把能量存进去，下坡时又把它取了出来。

还有一次，我在家里玩弹弓。

我把皮筋拉得长长的，然后松手，“嗖”的一下，石子就飞了出去。

拉皮筋的时候，我感觉到自己在用力，这是在储存能量。

当我松手的那一刻，储存的能量瞬间释放，转化成了石子的动能，让它飞得老远老远。

在生活中，能量守恒定律无处不在。

比如我们使用的电灯，电能转化为光能和热能；我们跑步时，体内的化学能转化为动能和热能。

甚至是我们吃东西，也是把食物中的化学能转化为身体所需的各种能量。

理论力学手写知识点总结一、质点运动1.1 质点的定义和性质质点是一个没有体积、形状和内部结构的物体，具有一定的质量和位置。

它的运动可以用一个固定点代表，这个点称为质点的质心。

质点的质量为m，位置用矢量r表示，r = x i + y j + z k。

1.2 质点的运动方程质点的运动方程描述了质点在运动过程中位置随时间的变化规律。

通常质点的运动方程可以写成r = r(t)，其中r为质点的位置矢量，t为时间。

在力学中，通过牛顿定律可得到质点的运动方程。

1.3 质点的速度和加速度质点的速度和加速度是描述质点运动状态的重要物理量。

质点的速度v定义为位置矢量r对时间的导数，即v = dr/dt；而加速度a定义为速度对时间的导数，即a = dv/dt。

1.4 一维运动的描述一维运动是指质点在一条直线上运动，可以用一个坐标系来描述质点的位置和运动规律。

对于一维运动，可以利用物理量的矢量分解和合成，对质点的位置、速度和加速度进行分析和计算。

1.5 相对运动相对运动是指两个或多个物体之间相互运动的问题。

对于相对运动问题，通常可以选取某个参照物来描述不同物体之间的相对位置和相对运动状态。

二、刚体运动2.1 刚体的概念和性质刚体是一个保持形状不变的物体，它可以看作是由无数个质点组成的系统。

刚体的运动包括平动和转动，同时刚体的平动运动可以看作是质点的集体运动。

2.2 刚体的平动运动刚体的平动运动是指刚体作为一个整体沿着直线或曲线运动的问题。

对于刚体的平动运动，可以用刚体的质心位置矢量来描述刚体的位置和运动规律。

2.3 刚体的转动运动刚体的转动运动是指刚体围绕一个固定轴线进行旋转的问题。

对于刚体的转动运动，可以用刚体的角位移、角速度和角加速度来描述刚体的转动状态和运动规律。

2.4 刚体的复合运动复合运动是指刚体同时进行平动和转动的问题。

对于刚体的复合运动，可以用刚体的质心位置矢量和角位移来描述刚体的位置和运动规律。

三、动力学3.1 牛顿定律牛顿定律是描述力学系统中物体运动规律的基本定律。

1. 力的作用:力是改变物体运动状态的原因，是使物体发
生形变或改变物体运动状态的原因。

2. 牛顿第一定律:一个物体会维持静止或匀速直线运动的
状态，除非有外力作用于它。

3. 牛顿第二定律:力等于质量乘以加速度，即F=ma。

4. 牛顿第三定律:对于每一个作用力，必有一个相等且反
向的反作用力。

5. 动能定理:动能等于物体的质量乘以速度平方再除以2。

6. 动量定理:动量的变化等于外力对物体做的功。

7. 能量守恒定律:能量在系统内总是守恒的，能量可以从
一种形式转化为另一种形式。

8. 机械波的传播规律:机械波沿传播方向发生周期性变化，振动方向与传播方向垂直。

9. 光的反射和折射规律:光线垂直于界面时会发生反射，
入射角等于反射角;光线斜着进入介质时会发生折射，入射角
小于折射角。

10. 波动光学基础:光是一种电磁波，具有波长、频率、
振幅等特性。

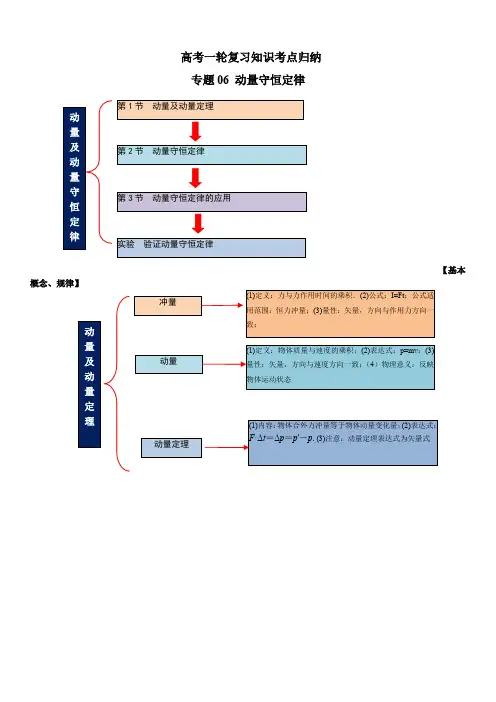
高考一轮复习知识考点归纳 专题06 动量守恒定律【基本概念、规律】动量及动量守恒定律第1节 动量及动量定理第2节 动量守恒定律第3节 动量守恒定律的应用实验 验证动量守恒定律(1)定义：力与力作用时间的乘积．(2)公式：I=Ft ；公式适用范围：恒力冲量；(3)量性：矢量，方向与作用力方向一致；动量及动量定理冲量动量动量定理(1)定义：物体质量与速度的乘积；(2)表达式：p=mv ；(3)量性：矢量，方向与速度方向一致；（4）物理意义：反映物体运动状态(1)内容：物体合外力冲量等于物体动量变化量；(2)表达式：F ·Δt ＝Δp ＝p ′－p . (3)注意：动量定理表达式为矢量式【重要考点归纳】考点一 动量定理的理解及应用1．动量定理不仅适用于恒定的力，也适用于随时间变化的力．这种情况下，动量定理中的力F 应理解为变力在作用时间内的平均值．2．动量定理的表达式F ·Δt ＝Δp 是矢量式，运用它分析问题时要特别注意冲量、动量及动量变化量的方向，公式中的F 是物体或系统所受的合力．3．应用动量定理解释的两类物理现象(1)当物体的动量变化量一定时，力的作用时间Δt 越短，力F 就越大，力的作用时间Δt 越长，力F 就越小，如玻璃杯掉在水泥地上易碎，而掉在沙地上不易碎．(2)当作用力F 一定时，力的作用时间Δt 越长，动量变化量Δp 越大，力的作用时间Δt 越短，动量变化量Δp 越小4.应用动量定理解题的一般步骤 (1)明确研究对象和研究过程．研究过程既可以是全过程，也可以是全过程中的某一阶段． (2)进行受力分析．只分析研究对象以外的物体施加给研究对象的力，不必分析内力． (3)规定正方向．(4)写出研究对象的初、末动量和合外力的冲量(或各外力在各个阶段的冲量的矢量和)，根据动量定理列方程求解．考点二 动量守恒定律与碰撞 1．动量守恒定律的不同表达形式守恒条件：(1)理想守恒：系统不受外力或所受外力的合力为零，则系统动量守恒．(2)近似守恒：系统受到的合力不为零，但当内力远大于外力时，系统的动量可近似看成守恒．(3)分方向守恒：系统在某个方向上所受合力为零时，系统在该方向上动量守恒．动量守恒定律动量守恒定律动量守恒应用1．碰撞 物体间的相互作用持续时间很短，而物体间相互作用力很大的现象．2．特点 在碰撞现象中，一般都满足内力远大于外力，可认为相互碰撞的系统动量守恒．动量守恒定律的表达式：m 1v 1＋m 2v 2＝m 1v ′1＋m 2v ′2或Δp 1＝－Δp 2.1．爆炸3．反冲 人船模型(1)p＝p′，系统相互作用前的总动量p等于相互作用后的总动量p′.(2)m1v1＋m2v2＝m1v′1＋m2v′2，相互作用的两个物体组成的系统，作用前的动量和等于作用后的动量和．(3)Δp1＝－Δp2，相互作用的两个物体动量的增量等大反向．(4)Δp＝0，系统总动量的增量为零．2．碰撞遵守的规律(1)动量守恒，即p1＋p2＝p′1＋p′2.(2)动能不增加，即E k1＋E k2≥E′k1＋E′k2或p212m1＋p222m2≥p′212m1＋p′222m2.(3)速度要合理．①碰前两物体同向，则v后>v前；碰后，原来在前的物体速度一定增大，且v′前≥v′后．②两物体相向运动，碰后两物体的运动方向不可能都不改变．3．两种碰撞特例(1)弹性碰撞两球发生弹性碰撞时应满足动量守恒和机械能守恒．以质量为m1、速度为v1的小球与质量为m2的静止小球发生正面弹性碰撞为例，则有m1v1＝m1v′1＋m2v′2①12m1v21＝12m1v′21＋12m2v′22②由①②得v′1＝m1－m2v1m1＋m2v′2＝2m1v1m1＋m2结论：①当m1＝m2时，v′1＝0，v′2＝v1，两球碰撞后交换了速度．②当m1>m2时，v′1>0，v′2>0，碰撞后两球都向前运动．③当m1<m2时，v′1<0，v′2>0，碰撞后质量小的球被反弹回来．(2)完全非弹性碰撞两物体发生完全非弹性碰撞后，速度相同，动能损失最大，但仍遵守动量守恒定律．4.应用动量守恒定律解题的步骤(1)明确研究对象，确定系统的组成(系统包括哪几个物体及研究的过程)；(2)进行受力分析，判断系统动量是否守恒(或某一方向上动量是否守恒)；(3)规定正方向，确定初、末状态动量；(4)由动量守恒定律列出方程；(5)代入数据，求出结果，必要时讨论说明．考点三爆炸和反冲人船模型1．爆炸的特点(1)动量守恒：由于爆炸是在极短的时间内完成的，爆炸时物体间的相互作用力远远大于受到的外力，所以在爆炸过程中，系统的总动量守恒．(2)动能增加：在爆炸过程中，由于有其他形式的能量(如化学能)转化为动能，所以爆炸后系统的总动能增加．(3)位移不变：爆炸的时间极短，因而作用过程中物体运动的位移很小，一般可忽略不计，可以认为爆炸后仍然从爆炸时的位置以新的动量开始运动．2．反冲(1)现象：物体的不同部分在内力的作用下向相反方向运动．(2)特点：一般情况下，物体间的相互作用力(内力)较大，因此系统动量往往有以下几种情况：①动量守恒；②动量近似守恒；③某一方向动量守恒．反冲运动中机械能往往不守恒．注意：反冲运动中平均动量守恒．(3)实例：喷气式飞机、火箭、人船模型等．3．人船模型若人船系统在全过程中动量守恒，则这一系统在全过程中的平均动量也守恒．如果系统由两个物体组成，且相互作用前均静止，相互作用后均发生运动，则由m1v1＝－m2v2得m1x1＝－m2x2.该式的适用条件是：(1)系统的总动量守恒或某一方向上的动量守恒．(2)构成系统的两物体原来静止，因相互作用而反向运动．(3)x1、x2均为沿动量方向相对于同一参考系的位移．实验：验证动量守恒定律1．实验原理在一维碰撞中，测出物体的质量m和碰撞前后物体的速率v、v′，找出碰撞前的动量p＝m1v1＋m2v2及碰撞后的动量p′＝m1v′1＋m2v′2，看碰撞前后动量是否守恒．2．实验方案方案一：利用气垫导轨完成一维碰撞实验(1)测质量：用天平测出滑块质量．(2)安装：正确安装好气垫导轨．(3)实验：接通电源，利用配套的光电计时装置测出两滑块各种情况下碰撞前后的速度(①改变滑块的质量．②改变滑块的初速度大小和方向)．(4)验证：一维碰撞中的动量守恒．方案二：利用等长悬线悬挂等大小球完成一维碰撞实验(1)测质量：用天平测出两小球的质量m1、m2.(2)安装：把两个等大小球用等长悬线悬挂起来．(3)实验：一个小球静止，拉起另一个小球，放下时它们相碰．(4)测速度：可以测量小球被拉起的角度，从而算出碰撞前对应小球的速度，测量碰撞后小球摆起的角度，算出碰撞后对应小球的速度．(5)改变条件：改变碰撞条件，重复实验．(6)验证：一维碰撞中的动量守恒．方案三：在光滑桌面上两车碰撞完成一维碰撞实验(1)测质量：用天平测出两小车的质量.(2)安装：将打点计时器固定在光滑长木板的一端，把纸带穿过打点计时器，连在小车的后面，在两小车的碰撞端分别装上撞针和橡皮泥．(3)实验：接通电源，让小车A运动，小车B静止，两车碰撞时撞针插入橡皮泥中，把两小车连接成一体运动．(4)测速度：通过纸带上两计数点间的距离及时间由v＝ΔxΔt算出速度．(5)改变条件：改变碰撞条件，重复实验．(6)验证：一维碰撞中的动量守恒．方案四：利用斜槽上滚下的小球验证动量守恒定律(1)用天平测出两小球的质量，并选定质量大的小球为入射小球．(2)按照如图所示安装实验装置，调整固定斜槽使斜槽底端水平．(3)白纸在下，复写纸在上，在适当位置铺放好．记下重垂线所指的位置O.(4)不放被撞小球，让入射小球从斜槽上某固定高度处自由滚下，重复10次．用圆规画尽量小的圆把所有的小球落点圈在里面，圆心P就是小球落点的平均位置．(5)把被撞小球放在斜槽末端，让入射小球从斜槽同一高度自由滚下，使它们发生碰撞，重复实验10次．用步骤(4)的方法，标出碰后入射小球落点的平均位置M和被碰小球落点的平均位置N.如图所示．(6)连接ON，测量线段OP、OM、ON的长度．将测量数据填入表中．最后代入m1OP＝m1OM＋m2ON，看在误差允许的范围内是否成立．(7)整理好实验器材放回原处．(8)实验结论：在实验误差范围内，碰撞系统的动量守恒．【思想方法与技巧】动量守恒中的临界问题1．滑块与小车的临界问题滑块与小车是一种常见的相互作用模型．如图所示，滑块冲上小车后，在滑块与小车之间的摩擦力作用下，滑块做减速运动，小车做加速运动．滑块刚好不滑出小车的临界条件是滑块到达小车末端时，滑块与小车的速度相同．2．两物体不相碰的临界问题两个在光滑水平面上做匀速运动的物体，甲物体追上乙物体的条件是甲物体的速度v甲大于乙物体的速度v乙，即v甲>v乙，而甲物体与乙物体不相碰的临界条件是v甲＝v乙．3．涉及弹簧的临界问题对于由弹簧组成的系统，在物体间发生相互作用的过程中，当弹簧被压缩到最短时，弹簧两端的两个物体的速度相等．4．涉及最大高度的临界问题在物体滑上斜面(斜面放在光滑水平面上)的过程中，由于弹力的作用，斜面在水平方向将做加速运动．物体滑到斜面上最高点的临界条件是物体与斜面沿水平方向具有共同的速度，物体在竖直方向的分速度等于零．5.正确把握以下两点是求解动量守恒定律中的临界问题的关键：(1)寻找临界状态看题设情景中是否有相互作用的两物体相距最近，避免相碰和物体开始反向运动等临界状态．(2)挖掘临界条件在与动量相关的临界问题中，临界条件常常表现为两物体的相对速度关系与相对位移关系，即速度相等或位移相等。

动量守恒定律笔记在学习物理的道路上，我就像一个在迷雾中摸索的旅人，而动量守恒定律就像是那穿透迷雾的一束光。

还记得最初接触动量守恒定律的时候，那可真是让我一头雾水。

老师在讲台上激情澎湃地讲解，我在下面听得云里雾里。

什么“一个系统不受外力或所受外力之和为零，这个系统的总动量保持不变”，这听起来就像是外星语言。

为了搞清楚这个定律，我决定自己动手做个小实验。

我找来了几个玩具小车，又从厨房拿来了几个大小差不多的土豆当作障碍物。

我把一辆蓝色的小车放在光滑的地板上，用力一推，小车就像脱缰的野马一样冲了出去。

然后，我在小车前进的路上放上一个土豆。

“砰”的一声，小车撞上了土豆，速度瞬间减慢，甚至还往后退了一点。

这可把我急坏了，这和动量守恒定律有啥关系呀？我不甘心，又进行了一次尝试。

这次我把两辆小车，一辆红色的和一辆绿色的，面对面放在一起。

我轻轻地推了一下红色的小车，让它慢慢地向绿色的小车移动。

当它们碰到一起的时候，神奇的事情发生了！红色的小车停了下来，而绿色的小车却以一定的速度向前驶去。

我瞪大眼睛，仔细观察着它们的运动，心里充满了疑惑和好奇。

经过一次又一次的尝试，我发现小车碰撞前后的速度和质量之间似乎有着某种神秘的联系。

就好像它们在进行一场“力量的博弈”，而这场博弈遵循着一定的规则，那就是动量守恒定律。

我开始仔细地记录每次实验的数据，计算小车碰撞前后的动量。

有时候算错了，我就气得直跺脚，嘴里嘟囔着：“这破数据，怎么就不对呢！”但我没有放弃，擦掉错误，重新再来。

在不断的尝试和计算中，我渐渐明白了动量守恒定律的真谛。

原来，动量不仅仅是速度和质量的简单乘积，它更是物体运动状态的一种度量。

当两个物体相互作用时，它们之间传递的不仅仅是力量，还有动量。

就像那次我用大力推蓝色小车，它的动量很大，撞上土豆后，一部分动量被土豆“吸收”了，所以小车的速度就减慢了。

而两辆小车面对面碰撞时，它们的动量在碰撞的瞬间进行了重新分配，总动量却始终保持不变。

动量定理笔记在学习物理的旅程中，动量定理就像是一位神秘而有趣的朋友，总是给我带来各种惊喜和挑战。

记得那是一个阳光明媚的上午，物理课的铃声像往常一样清脆地响起。

老师带着一脸神秘的笑容走进教室，然后在黑板上写下了“动量定理”四个大字。

当时的我，心里还在嘀咕：“这又是什么高深的玩意儿？”老师开始讲解，他说：“同学们，想象一下，一辆飞速行驶的汽车突然刹车，为什么车上的人会往前倾？又或者，一个小球撞到另一个静止的小球，它们的运动状态会发生怎样的变化？这背后都隐藏着动量定理的奥秘。

”我听得云里雾里，满脑子都是问号。

为了让我们更好地理解，老师决定做一个实验。

他拿出一个小推车，上面放着一些砝码，然后用力一推。

小推车就像脱缰的野马一样在桌面上飞奔起来。

“大家注意看，现在小推车有速度，也就有了动量。

”老师一边操作一边讲解。

接着，他在小推车前进的路上放了一块海绵，小推车撞到海绵后，速度明显减慢了。

“看，这就是外力作用改变了动量。

”我紧紧地盯着那个小推车，眼睛都不敢眨一下，生怕错过了什么重要的细节。

只见老师又改变了砝码的数量，再次推动小推车。

这次，小推车的速度和之前不一样了。

“同学们，砝码的多少改变了小推车的质量，质量不同，动量也就不同啦。

”实验结束后，老师开始在黑板上写公式。

我赶紧拿起笔，想要把这些都记下来。

“动量的改变等于合外力乘以作用时间，这就是动量定理，大家记住了啊！”老师的声音在教室里回荡。

可我发现，仅仅记住公式是远远不够的，要真正理解动量定理，还得自己多琢磨琢磨。

放学后，我回到家，看到弟弟正在玩玩具车。

突然，我灵机一动，决定用弟弟的玩具车来再体会一下动量定理。

我把玩具车放在地上，用力一推，然后观察它的运动。

接着，我又用不同的力气去推，还改变了车上玩具小人的数量，就像在课堂上老师改变砝码数量一样。

玩着玩着，我好像有点明白动量定理是怎么回事了。

比如，我用很大的力气去推玩具车，它就跑得很快很远；如果车上的玩具小人多了，也就是质量大了，推起来就更费劲，跑的速度也相对慢一些。

九年级下册物理知识点手写笔记一、力的作用与效果1. 力的定义：力是任何物体或系统能够改变自身运动状态或形状的原因。

2. 受力与施力：力都是相互作用力，即存在施力物体和受力物体。

3. 作用力与反作用力：根据牛顿第三定律，作用力与反作用力大小相等、方向相反。

4. 力的效果：力可以使物体改变速度、形状或者产生变形、移动物体等。

二、动量与动量守恒定律1. 动量的定义：物体的动量是其质量和速度的乘积，用公式表示为P = mv，其中P表示动量，m表示质量，v表示速度。

2. 动量变化：当物体的质量或速度发生变化时，动量也会发生变化。

3. 动量守恒定律：在一个封闭系统中，如果没有外力作用，系统的总动量保持不变。

4. 弹性碰撞和非弹性碰撞：弹性碰撞指碰撞后物体恢复原状，动量守恒成立；非弹性碰撞指碰撞后物体发生变形，动量守恒仍然成立，但动能不守恒。

三、功与机械能1. 功的定义：当力作用于物体上时，力对物体所做的功是指使物体移动的能力。

2. 功的计算：功等于力乘以物体的位移，用公式表示为W =F×s，其中W表示功，F表示力，s表示位移。

3. 机械能：机械能是指物体具有的可以执行功的能力，包括动能和势能。

4. 动能和势能：动能是物体运动时具有的能量，用公式表示为E_k = 1/2mv^2，其中E_k表示动能，m表示质量，v表示速度；势能是物体在静止状态下的能量，常见的有重力势能和弹性势能。

四、压强与浮力1. 压强的定义：压强是单位面积上的力的大小，用公式表示为P = F/A，其中P表示压强，F表示力，A表示面积。

2. 压力的应用：压力对物体产生的效果有压扁、压碎和变形等。

3. 浮力的产生：浮力是物体在液体或气体中的受力，是受到上方液体或气体向下的压力。

4. 浮力原理：物体在液体中的浮力等于物体所排除液体的重量，用公式表示为F_b = ρfVg，其中F_b表示浮力，ρf表示液体的密度，V表示受浸没的物体的体积，g表示重力加速度。

第二节动量定理[学习目标] 1.理解冲量的定义及动量定理的确切含义.2.理解分析生活中的缓冲现象，掌握动量定理的应用.3.理解冲量和功、动量定理和动能定理的区别．一、动量定理1．内容：物体所受合力的冲量等于物体动量的改变量．2．表达式：Ft＝m v t－m v0.3．适用范围：动量定理不但适用于恒定的外力，而且适用于随时间而变化的变力．在后一种情况下，动量定理中的力F通常取作用时间内的平均值．二、动量定理的应用动量定理只考虑物体相互作用的始末状态，不考虑具体过程和细节．在涉及力、力的作用时间、速度的问题时，采用动量定理处理问题比较简捷．1．判断下列说法的正误．(1)若物体在一段时间内动量发生了变化，则物体在这段时间内受到的合外力一定不为零．(√)(2)某人跳远时，跳在沙坑里比跳在水泥地上安全，这是由于人跳到沙坑里受到的冲量比跳在水泥地上小．(×)(3)瓦工师傅贴墙砖时，为了使墙砖平整，往往用橡皮锤敲打墙砖，而不是用铁锤，是因为橡皮锤产生的冲量小．(×)(4)篮球运动员通常伸出双手迎接传来的篮球，接球时两手随球迅速收缩至胸前，这样做可以减小球的动量的变化率，保护运动员的安全．(√)2．在一条直线上运动的物体，其初动量为8 kg·m/s，它在第1 s内受到的冲量为－3 N·s，第2 s内受到的冲量为5 N·s，它在第2 s末的动量为________ kg·m/s.答案10解析根据动量定理得：I1＋I2＝p－m v0，则p＝I1＋I2＋m v0＝(－3＋5＋8) kg·m/s＝10 kg·m/s.一、动量定理的理解1．动量定理反映了合外力的冲量是动量变化的原因．2．动量定理的表达式Ft＝m v t－m v0是矢量式，在一维情况下运用动量定理解题时，要注意规定正方向．3．公式中的F是物体所受的合外力，若合外力是均匀变化的力，则F应是合外力在作用时间内的平均值．(多选)对下列几种物理现象的解释，正确的是()A．击钉时，不用橡皮锤仅仅是因为橡皮锤太轻B．用手接篮球时，手往往向后缩一下，是为了减小冲量C．易碎品运输时，要用柔软材料包装，船舷常常悬挂旧轮胎，都是为了延长作用时间以减小作用力D．在车内推车推不动，是因为车(包括人)所受合外力的冲量为零答案CD解析击钉时，不用橡皮锤是因为橡皮锤与钉子的作用时间长，作用力小；用手接篮球时，手往后缩一下，是为了延长作用时间以减小作用力，A、B项错误；据动量定理F·t＝Δp知，当Δp相同时，t越长，作用力越小，C项正确；车能否移动或运动状态能否改变取决于所受的合外力，与内部作用无关，D项正确．(多选)A、B两球质量相等，A球竖直上抛，B球平抛，两球运动过程中空气阻力不计，则在落地前下列说法正确的是()A．相等时间内，动量的变化大小相等、方向相同B ．相等时间内，动量的变化大小相等、方向不同C ．动量的变化率大小相等、方向相同D ．动量的变化率大小相等、方向不同答案 AC解析 A 、B 两球在运动过程中只受重力作用，相等时间内重力的冲量相同，因此在相等时间内两球动量的变化大小相等、方向相同，A 选项正确，B 选项错误；动量的变化率为Δp Δt ＝m Δv Δt＝mg ，大小相等、方向相同，C 选项正确，D 选项错误．二、动量定理的应用1．定性分析有关现象(1)物体的动量变化量一定时，力的作用时间越短，力就越大，反之力就越小．(2)作用力一定时，力的作用时间越长，动量变化量越大，反之动量变化量就越小．2．应用动量定理定量计算的一般步骤选定研究对象，明确运动过程→进行受力分析，确定初、末状态→选取正方向，确定各矢量符号，列动量定理方程求解质量为0.2 kg 的小球以6 m /s 、竖直向下的速度落至水平地面上，再以4 m/s 的速度反向弹回．取竖直向上为正方向，g 取10 m/s 2.(1)求小球与地面碰撞前后瞬间动量的变化量； (2)若小球与地面的作用时间为0.2 s ，求小球受到地面的平均作用力大小．答案 (1)2 kg·m/s ，方向竖直向上 (2)12 N解析 (1)取竖直向上为正方向，则初动量为负，末动量为正，动量的变化量为Δp ＝p ′－p ＝0.2×4 kg·m /s －0.2×(－6) kg·m/s ＝2 kg·m/s ，方向竖直向上．(2)由动量定理得(F －mg )t ＝Δp ，解得F ＝Δp t ＋mg ＝20.2N ＋0.2×10 N ＝12 N.用动量定理解题时应注意的问题1．列方程前首先选取正方向；2．分析速度时一定要选取同一参考系，一般选地面为参考系；3．公式中的冲量应是合外力的冲量，求动量的变化量时要严格按公式，且要注意动量的变化量是末动量减去初动量．在水平力F ＝30 N 的作用下，质量m ＝5 kg 的物体由静止开始沿水平面运动．已知物体与水平面间的动摩擦因数μ＝0.2，若F 作用6 s 后撤去，撤去F 后物体还能向前运动多长时间才停止？(g 取10 m/s 2)答案 12 s解析 解法一 用动量定理，分段求解．选物体为研究对象，对于撤去F 前物体做匀加速运动的过程，初态速度为零，末态速度为v .取水平力F 的方向为正方向，根据动量定理有(F －μmg )t 1＝m v －0，对于撤去F 后物体做匀减速运动的过程，初态速度为v ，末态速度为零．根据动量定理有－μmgt 2＝0－m v .联立解得t 2＝F －μmg μmg t 1＝30－0.2×5×100.2×5×10×6 s ＝12 s. 解法二 用动量定理，研究全过程．选物体为研究对象，研究整个运动过程，这个过程的始、末状态物体的速度都等于零． 取水平力F 的方向为正方向，根据动量定理得(F －μmg )t 1＋(－μmg )t 2＝0解得t 2＝F －μmg μmg t 1＝30－0.2×5×100.2×5×10×6 s ＝12 s.三、用动量定理处理流体问题有一宇宙飞船，它的正对面积S ＝2 m 2，以v ＝3×103 m/s 的速度飞入一宇宙微粒区．此微粒区平均1 m 3中有一个微粒，每一个微粒的平均质量为m ＝2×10－6 kg.设微粒与飞船外壳碰撞后附着于飞船上，要使飞船速度不变，飞船的牵引力应增加( )A ．36 NB ．3.6 NC ．12 ND ．1.2 N答案 A解析 取时间Δt 内与飞船碰撞的微粒为研究对象，其质量应等于底面积为S 、高为v Δt 的圆柱体内微粒的质量，即M ＝mS v Δt ，其初动量为0，末动量为M v .设飞船对微粒的作用力为F ，由动量定理得，F ·Δt ＝M v －0，则F ＝M v Δt ＝mS v Δt ·v Δt＝mS v 2；根据牛顿第三定律可知，微粒对飞船的撞击力大小也等于mS v 2，则飞船牵引力应增加F ′＝F ＝mS v 2；代入数据得：F ′＝2×10－6×2×(3×103)2 N ＝36 N.动量定理处理流体问题的思路1．在极短时间Δt 内，取“流体”的一段小柱体为研究对象．2．求出小柱体的质量：Δm ＝ρΔV ＝ρS v Δt3．小柱体动量变化量的大小：Δp ＝Δm v ＝ρS v 2Δt4．应用动量定理F Δt ＝Δp 求作用力.1．(利用动量定理定性分析实际问题)(2020·重庆市万州第一中学高一期末)交通管理法规规定：骑摩托车必须戴好头盔，这样做的目的是保护交通事故中的车手，理由是( )A ．减小头部的冲量，起到安全作用B ．延长头部与硬物的接触时间，从而减小冲力，起到保护作用C ．减小头部的速度变化使人安全D ．减小头部的动量变化量，起到安全作用答案 B解析 戴和不戴头盔，头部的速度变化相同，则动量变化量相同，根据动量定理可知，受到的冲量也相同，而戴头盔能够延长头部与硬物的接触时间，根据F Δt ＝Δp 可知，可以减小冲力，从而起到保护作用，故B 正确，A 、C 、D 错误．2．(动量定理的应用)(2018·全国卷Ⅱ)高空坠物极易对行人造成伤害．若一个50 g 的鸡蛋从一居民楼的25层坠下，与地面的碰撞时间约为2 ms ，则该鸡蛋对地面产生的冲击力约为( )A ．10 NB ．102 NC ．103 ND ．104 N答案 C3．(应用动量定理处理流体问题)(2020·河北辛集中学高三上月考)超强台风“利奇马”在 2019年8月10日凌晨1点45分前后在浙江温岭沿海登陆，登陆时中心附近的最大风力 16级(52米/秒)，是新中国成立之后登陆我国强度排第五的超强台风，风力大，降水强度大，影响范围广，涉及10个省区市，持续时间长，也是历史上少有的超强台风，对固定建筑物破坏程度巨大．请你根据所学物理知识推算固定建筑物所受风力(空气的压力)与风速(空气流动速度)大小的关系．假设某一建筑物垂直风速方向的受力面积为S ，风速大小为v ，风吹到建筑物上后速度瞬间减为零，空气密度为ρ，则风力F 与风速大小v 的关系式为( )A ．F ＝ρS vB ．F ＝ρS v 2C ．F ＝12ρS v 3 D ．F ＝ρS v 3答案 B解析 设t 时间内吹到建筑物上的空气质量为m ，则有m ＝ρS v t ，根据动量定理可得－Ft ＝0－m v ＝0－ρS v 2t ，解得风力F 与风速大小v 的关系式为F ＝ρS v 2，故选B.4．(动量定理的应用)(2020·广西防城港市防城中学期中)一辆轿车以30 m/s 的速度行驶时，与另一辆迎面驶来的轿车相撞，相撞后两车均停下来，已知作用时间为0.025 s.(1)求车祸中车内质量m ＝60 kg 的人受到的平均冲力的大小；(2)若此人系有安全带，安全带在车祸过程中与人体的作用时间是1 s，求这种情况下人受到的平均冲力与不系安全带时人受到的平均冲力之比．答案(1)7.2×104 N(2)1∶40解析(1)设人受到的平均冲力大小为F，以轿车原来速度的方向为正方向根据动量定理有－Ft＝0－m v0解得F＝7.2×104 N(2)若人系有安全带，同理可得－F′t′＝－m v0解得F′＝1.8×103 N则F′∶F＝1∶40.考点一动量定理的理解1．(多选)关于动量和冲量的说法，正确的是()A．物体所受合外力冲量越大，它的动量也越大B．物体所受合外力冲量不为零，它的动量一定要改变C．物体动量变化的方向，就是它所受合外力的冲量方向D．物体所受合外力冲量越大，它的动量变化就越大答案BCD解析由动量定理可知，物体所受合外力的冲量的大小等于动量变化的大小，方向与动量变化的方向相同，故A项错误，B、C、D项正确．2．(2020·全国卷Ⅰ)行驶中的汽车如果发生剧烈碰撞，车内的安全气囊会被弹出并瞬间充满气体．若碰撞后汽车的速度在很短时间内减小为零，关于安全气囊在此过程中的作用，下列说法正确的是()A．增加了司机单位面积的受力大小B．减少了碰撞前后司机动量的变化量C．将司机的动能全部转换成汽车的动能D．延长了司机的受力时间并增大了司机的受力面积答案D解析汽车剧烈碰撞瞬间，安全气囊弹出，立即跟司机身体接触．司机在很短时间内由运动到静止，动量的变化量是一定的，由于安全气囊的存在，作用时间变长，根据动量定理Δp ＝FΔt知，司机所受作用力减小；又知安全气囊打开后，司机受力面积变大，因此减小了司机单位面积的受力大小；碰撞过程中，动能转化为内能．综上可知，选项D正确．3.如图1所示，重物G压在纸带上，用一水平力缓慢地拉动纸带，重物G会跟着一起运动；若迅速拉动纸带，纸带将会从重物G下面抽出，关于这个现象，下列说法中正确的是()图1A．在缓慢拉动纸带时，重物和纸带间的摩擦力大于迅速拉动纸带时重物和纸带间的摩擦力B．在缓慢拉动纸带时，纸带对重物的冲量大C．在迅速拉动纸带时，纸带对重物的冲量大D．迅速拉动纸带时重物的动量变化大答案B解析用水平力F慢慢拉动纸带，重物与纸带间有静摩擦力，若迅速拉动纸带，纸带会从重物下抽出，重物与纸带间有滑动摩擦力，滑动摩擦力大于或等于静摩擦力，故A错误；缓慢拉动纸带时，重物跟着纸带运动，动量变化大，故缓慢拉时纸带对重物的摩擦力的冲量大，由于作用时间长，支持力的冲量也大，故缓慢拉时，纸带对重物的冲量大，故B正确，C、D错误．考点二动量定理的应用4．(多选)(2020·江苏如皋高二上调研)运动员挥拍将质量为m的网球击出．如果网球被球拍击打前、后瞬间速度的大小分别为v1、v2，v1与v2方向相反，且v2>v1.重力影响可忽略，则此过程中球拍对网球作用力的冲量()A．大小为m(v2＋v1) B．大小为m(v2－v1)C．方向与v1方向相同D．方向与v2方向相同答案AD解析以v1的方向为正方向，则球拍对网球作用力的冲量为I＝－m v2－m v1＝－m(v1＋v2)，则冲量的大小为m(v1＋v2)，方向与v1方向相反，与v2方向相同，选项A、D正确，B、C错误．5．(多选)(2020·石家庄二中高二上月考)质量为m的物体以初速度v0开始做平抛运动，经过时间t，下降的高度为h，速度变化为v，在这段时间内物体动量变化量的大小可能是(重力加速度为g)()A．m(v－v0) B．mgtC．m v2－v02D．m2gh答案BCD解析根据动量定理，物体动量的变化量等于末动量与初动量的矢量差，而不是代数差，A 错误；由动量定理I合＝Δp知Δp＝mgt，B正确；Δp＝mΔv＝m v y＝m v2－v02＝m2gh，C、D正确．6．(2020·内蒙古集宁一中高二月考)甲、乙两物体分别在恒力F1和F2的作用下沿同一直线运动，它们的动量随时间的变化关系如图2所示，设甲在t1时间内所受的冲量为I1，乙在t2时间内所受的冲量为I2，则下列F、I的关系正确的是()图2A ．F 1<F 2，I 1<I 2B ．F 1>F 2，I 1>I 2C ．F 1>F 2，I 1＝I 2D ．F 1＝F 2，I 1＝I 2答案 C 解析 由题图图像可知，甲、乙两物体动量变化量的大小相等，根据动量定理知，冲量的大小相等，即I 1＝I 2；根据I ＝F Δt 知，作用时间长的力较小，则有F 1>F 2，故选C.7.(2020·济南市历城第二中学高三月考)地动仪是世界上最早的感知地震装置，由我国杰出的科学家张衡在洛阳制成，早于欧洲1700多年．如图3所示，为一现代仿制的地动仪，龙口中的铜珠到蟾蜍口的距离为h ，当感知到地震时，质量为m 的铜珠(初速度为零)离开龙口，落入蟾蜍口中，与蟾蜍口碰撞的时间约为t ，重力加速度为g ，不计空气阻力，则铜珠对蟾蜍口产生的冲击力大小约为( )图3 A.m 2gh t＋mg B.m 2gh t C.m gh tD.m gh t －mg 答案 A解析 铜珠做自由落体运动，落到蟾蜍口的速度为：v ＝2gh设蟾蜍口对铜珠的作用力为F ，以竖直向上为正方向，根据动量定理可知：Ft －mgt ＝0－(－m v )解得：F ＝m 2gh t＋mg ，根据牛顿第三定律可知，铜珠对蟾蜍口产生的冲击力大小F ′＝F ，A 正确．8．(2020·福建三元三明一中期中)人们对手机的依赖性越来越强，如图4所示，有些人喜欢躺着看手机，经常出现手机砸伤眼睛的情况．若手机质量为120 g ，从离人眼约20 cm 的高度无初速度掉落，砸到眼睛后手机未反弹，眼睛受到的手机的冲击时间约为0.2 s ，取重力加速度g ＝10 m/s 2，下列分析正确的是( )图4A ．手机与眼睛作用过程中手机动量变化约为0.48 kg·m/sB ．手机对眼睛的冲量大小约为0.48 N·sC ．手机对眼睛的冲量方向竖直向上D ．手机对眼睛的作用力大小约为0.24 N答案 B解析 根据自由落体运动规律得v ＝2gh ＝2×10×0.2 m /s ＝2 m/s ，选取向上为正方向，手机与眼睛作用后手机的速度变成0，所以手机与眼睛作用过程中动量变化为Δp ＝0－(－m v )＝0.12×2 kg·m /s ＝0.24 kg·m/s ，A 错误；手机与眼接触的过程中受到重力与眼睛的作用力，由动量定理得I y －mgt ＝Δp ，代入数据可得：I y ＝0.48 N·s ，眼睛对手机的作用力F ＝I y t ＝0.480.2N ＝2.4 N ，手机对眼睛的作用力与眼睛对手机的作用力大小相等，方向相反，作用的时间相等，所以手机对眼睛的冲量大小约为0.48 N·s ，作用力大小约为2.4 N ，方向竖直向下，故B 正确，C 、D 错误．9．(2019·全国卷Ⅰ)最近，我国为“长征九号”研制的大推力新型火箭发动机联试成功，这标志着我国重型运载火箭的研发取得突破性进展．若某次实验中该发动机向后喷射的气体速度约为3 km/s ，产生的推力约为4.8×106 N ，则它在1 s 时间内喷射的气体质量约为( )A ．1.6×102 kgB ．1.6×103 kgC ．1.6×105 kgD ．1.6×106 kg答案 B解析 设1 s 时间内喷出的气体的质量为m ，喷出的气体与该发动机的相互作用力为F ，由动量定理有Ft ＝m v －0，则m ＝Ft v ＝4.8×106×13×103kg ＝1.6×103 kg ，选项B 正确． 10．(多选)如图5所示，质量为m 的小球从距离地面高H 的A 点由静止开始释放，落到地面上后又陷入泥潭中，由于受到阻力作用，到达距地面深度为h 的B 点速度减为零．不计空气阻力，重力加速度为g .关于小球下落的整个过程，下列说法中正确的是( )图5A ．小球的机械能减少了mg (H ＋h )B ．小球克服阻力做的功为mghC ．小球所受阻力的冲量大于m 2gHD ．小球动量的变化量等于所受阻力的冲量答案 AC解析 在整个过程中，小球动能变化量为零，重力势能减小mg (H ＋h )，则小球的机械能减小了mg (H ＋h )，所以A 正确；对全过程运用动能定理得，mg (H ＋h )－W F ＝0，则小球克服阻力做功W F ＝mg (H ＋h )，故B 错误；根据运动学规律，小球落到地面的速度v ＝2gH ，对进入泥潭的过程运用动量定理得：I G －I F ＝0－m 2gH ，可知阻力的冲量为：I F ＝I G ＋m 2gH ，即大于m 2gH ，故C 正确；对全过程分析，运用动量定理知，动量的变化量等于重力的冲量和阻力冲量的矢量和，故D 错误．11．(2020·湖南常德期中联考)原来静止的物体受合外力作用的时间为2t 0，作用力随时间的变化情况如图6所示，则( )图6A ．0～t 0时间内物体的动量变化与t 0～2t 0时间内动量变化相同B ．0～t 0时间内物体的平均速率与t 0～2t 0时间内平均速率不相等C ．t ＝2t 0时物体的瞬时速度为零，外力在0～2t 0时间内对物体的冲量为零D ．0～2t 0时间内物体的位移为零，外力对物体做功为零答案 C解析 0～t 0与t 0～2t 0内作用力方向不同，故动量变化量不相同，A 错误．t ＝t 0时物体速度最大，t ＝0和t ＝2t 0时物体速度都为零，两段时间内平均速率相等；又I ＝F 0t 0－F 0t 0＝0，故B 错误，C 正确.0～2t 0时间内，物体先加速后减速，位移不为零，W 总＝ΔE k ＝0，D 错误．12.水刀切割具有精度高、无热变形、无手刺、无需二次加工以及节约材料等特点，得到广泛应用．某水刀切割机床如图7所示，若横截面直径为d 的水流以速度v 垂直射到要切割的钢板上，碰到钢板后水的速度减为零，已知水的密度为ρ，忽略水流重力的影响，则钢板受到水的冲击力大小为( )图7A ．πρd 2vB ．πρd 2v 2 C.14πρd 2v D.14πρd 2v 2 答案 D解析 设t 时间内有V 体积的水打在钢板上，则这些水的质量为m ＝ρV ＝ρS v t ＝14πd 2ρv t ，以这部分水为研究对象，它受到钢板的作用力为F ，以水运动的方向为正方向，由动量定理有Ft ＝0－m v ，解得F ＝－m v t ＝－14πd 2ρv 2，则由牛顿第三定律得钢板受到水的冲击力大小为 14πd 2ρv 2，故选D. 13．(2020·山东高二月考)高空抛物现象曾被称为“悬在城市上空的痛”.2020年5月28日十三届全国人大三次会议表决通过了《中华人民共和国民法典》，自2021年1月1日起施行关于高空抛物的新规定，明确侵权人依法承担的责任．高空抛物的危害究竟有多大呢？让我们通过数据说明．若质量为0.2 kg的苹果，从一居民楼的16层坠下．假设每层楼的高度为3 m，则苹果下落的高度为45 m，重力加速度为10 m/s2，不计空气阻力．(1)苹果撞击地面的过程中，求苹果的动量变化量(取竖直向下为正方向)；(2)若苹果与地面碰撞时间约为1.2×10－3 s，求苹果对地面的撞击力大小．答案(1)－6 kg·m/s，方向竖直向上(2)5 002 N解析(1)设苹果撞击地面前瞬间速度为v，由v＝2gh，解得v＝30 m/s，苹果的末速度为0，则苹果撞击地面的过程中动量变化量Δp＝0－mv，可得Δp＝－6 kg·m/s，方向竖直向上．(2)设苹果撞击地面的过程中，地面对苹果的撞击力大小为F，由动量定理得(mg－F)Δt＝0－m v，代入数据得F＝5 002 N，根据牛顿第三定律，地面对苹果的撞击力与苹果对地面的撞击力大小相等，方向相反，故苹果对地面的撞击力大小F′＝5 002 N.14.如图8所示，质量m＝2 kg的物体，在水平力F＝8 N的作用下由静止开始沿水平面向右运动，已知物体与水平面间的动摩擦因数μ＝0.2，若F作用了t1＝6 s后撤去，撤去F后又经t2＝2 s物体与竖直墙相碰，若物体与墙壁作用时间t3＝0.1 s，碰墙后反向弹回的速度大小v′＝6 m/s，求墙壁对物体的平均作用力大小．(g取10 m/s2)图8答案280 N解析选物体为研究对象，在t1时间内其受力情况如图甲所示，撤去F后，物体受力如图乙所示，选F的方向为正方向，根据动量定理得：(F－μmg)t1－μmgt2＝m v解得v ＝8 m/s物体与墙壁作用后速度变为向左，根据动量定理得 F t 3＝－m v ′－m v解得F ＝－280 N故墙壁对物体的平均作用力大小为280 N.15．人们常说“滴水穿石”，请你根据下面所提供的信息，估算水对石头的冲击力的大小．一瀑布落差为h ＝20 m ，水流量为Q ＝0.10 m 3/s ，水的密度ρ＝1.0×103 kg/m 3，水在最高点和落至石头上后的速度都认为是零．(落在石头上的水立即流走，在讨论石头对水的作用时可以不考虑水的重力，g 取10 m/s 2)答案 2×103 N解析 设水滴下落与石头碰前速度为v ，则有mgh ＝12m v 2，故v ＝2gh 设时间Δt 内有质量为Δm 的水冲到石头上，石头对水的作用力为F ，以竖直向下为正方向，由动量定理得：－F Δt ＝0－Δm v又因Δm ＝ρQ Δt联立得：F ＝ρQ 2gh ＝2×103 N由牛顿第三定律知，水对石头的作用力：F ′＝F ＝2×103 N ，方向竖直向下．。

选修3-5动量知识点总结一、对冲量的理解1、I =Ft ：适用于计算恒力或平均力F 的冲量，变力的冲量常用动量定理求。

2、I 合 的求法：A 、若物体受到的各个力作用的时间相同，且都为恒力，则I 合=F 合.tB 、若不同阶段受力不同，则I 合为各个阶段冲量的矢量和。

1、意义：冲量反映力对物体在一段时间上的积累作用，动量反映了物体的运动状态。

2、矢量性：ΔP 的方向由v ∆决定，与1p 、2p 无必然的联系，计算时先规定正方向。

三、对动量守恒定律的理解：1、研究对象：相互作用的物体所组成的系统2、条件： A 、理想条件：系统不受外力或所受外力有合力为零。

B 、近似条件：系统内力远大于外力，则系统动量近似守恒。

C 、单方向守恒：系统单方向满足上述条件，则该方向系统动量守恒。

四、碰撞类型及其遵循的规律：结论：等质量 弹性正碰 时，两者速度交换。

依据：动量守恒、动能守恒五、判断碰撞结果是否可能的方法：碰撞前后系统动量守恒；系统的动能不增加；速度符合物理情景。

动能和动量的关系：mp E K 22= K mE p 2=六、反冲运动：1、定义：静止或运动的物体通过分离出一部分物体，使另一部分向反方向运动的现象叫反冲运动。

2、规律：系统动量守恒3、人船模型：条件：当组成系统的2个物体相互作用前静止，相互作用过程中满足动量守恒。

七、临界条件：“最”字类临界条件如压缩到最短、相距最近、上升到最高点等的处理关键是——系统各组成部分具有共同的速度v 。

八、动力学规律的选择依据：1、题目涉及时间t ，优先选择动量定理；2、题目涉及物体间相互作用，则将发生相互作用的物体看成系统，优先考虑动量守恒；3、题目涉及位移s ，优先考虑动能定理、机械能守恒定律、能量转化和守恒定律；4、题目涉及运动的细节、加速度a ，则选择牛顿运动定律+运动学规律；九、表达规范：说明清楚研究对象、研究过程、规律、规定正方向。

典型练习一、基本概念的理解：动量、冲量、动量的改变量1、若一个物体的动量发生了改变，则物体的（ ） A 、速度大小一定变了 B 、速度方向一定变了 C 、速度一定发生了改变 D 、加速度一定不为02、质量为m 的物体从光滑固定斜面顶端静止下滑到底端，所用的时间为t, 斜面倾角为θ。

动量定理模块知识点总结一、动量概念及其理解（1）定义：物体的质量及其运动速度的乘积称为该物体的动量p=mv（2）特征：①动量是状态量，它与某一时刻相关；②动量是矢量，其方向与物体运动速度的方向相同。

（3）意义：速度从运动学角度量化了机械运动的状态,动量则从动力学角度量化了机械运动的状态。

二、冲量概念及其理解（1）定义：某个力与其作用时间的乘积称为该力的冲量I=F△t（2）特征：①冲量是过程量，它与某一段时间相关；②冲量是矢量，对于恒力的冲量来说，其方向就是该力的方向。

（3）意义：冲量是力对时间的累积效应。

对于质量确定的物体来说，合外力决定着其速度将变多快；合外力的冲量将决定着其速度将变多少。

对于质量不确定的物体来说，合外力决定着其动量将变多快；合外力的冲量将决定着其动量将变多少。

三、动量定理：F ·t = m v2 –m v1F·t是合外力的冲量，反映了合外力冲量是物体动量变化的原因．（1）动量定理公式中的F·t是合外力的冲量，是使研究对象动量发生变化的原因;（2）在所研究的物理过程中，如作用在物体上的各个外力作用时间相同，求合外力的冲量可先求所有力的合外力，再乘以时间，也可求出各个力的冲量再按矢量运算法则求所有力的会冲量;（3）如果作用在被研究对象上的各个外力的作用时间不同，就只能先求每个外力在相应时间内的冲量，然后再求所受外力冲量的矢量和．（4）要注意区分“合外力的冲量”和“某个力的冲量”，根据动量定理，是“合外力的冲量”等于动量的变化量，而不是“某个力的冲量”等于动量的变化量（注意）。

1.质量为m 的钢球自高处落下，以速率v 1碰地，竖直向上弹回，碰掸时间极短，离地的速率为v 2。

在碰撞过程中，地面对钢球冲量的方向和大小为（ D ）A 、向下，m(v 1-v 2)B 、向下，m(v 1+v 2)C 、向上，m(v 1-v 2)D 、向上，m(v 1+v 2)2．一辆空车和一辆满载货物的同型号的汽车，在同一路面上以相同的速度向同一方向行驶．紧急刹车后(即车轮不滚动只滑动)那么 (C D )A ．货车由于惯性大，滑行距离较大B ．货车由于受的摩擦力较大，滑行距离较小C ．两辆车滑行的距离相同D ．两辆车滑行的时间相同3．一个质量为0.3kg 的小球，在光滑水平面上以6m/s 的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小为4m/s 。