当前位置：文档之家 › 八上特殊三角形难题课件.doc

八上特殊三角形难题课件.doc

  • 格式：doc
  • 大小：960.00 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

河北省2024八年级数学上册第十七章特殊三角形拔高练三角形中的动态问题课件新版冀教版

河北省2024八年级数学上册第十七章特殊三角形拔高练三角形中的动态问题课件新版冀教版
CD ，直接写出∠ AEG 与
∠ ACD 的数量关系.
1
2
(2)①解：同(1)可证，△ BAD ≌△ CAE ，
∴∠ ABD ＝∠ ACE . ∵∠ AFB ＝∠ CFO ，∠ ABF ＋∠ AFB
＋∠ BAC ＝∠ FCO ＋∠ CFO ＋∠ BOC ＝180°，
∴∠ BOC ＝∠ BAC ＝70°.
∴ PB ＝ BC － PC ＝6 －6. 1 2
③当 AQ ＝ PQ 时，如图②，∠ QAP ＝∠ QPA ＝45°.
∵∠ BAP ＝∠ BAC －∠ QAP ＝45°，∴∠ APB ＝


90°.∵ AB ＝ AC ， AP ⊥ BC ，∴ PB ＝ PC ＝ BC ＝3
.综上所述， PB 的长度为0或6 －6或3 .
∵0°≤∠ BAP ＜90°，∠ B ＝45°，
∴45°≤∠ BAP ＋∠ B ＜45°＋90°＝135°，
∴45°≤∠ APC ＜135°. 1 2
2. [2023保定期中]如图，在△ ABC 中，∠ BAC ＝90°，
AB ＝ AC ＝6， BC ＝6 ，点 P 从点 A 出发以每秒1个
单位长度的速度沿折线 AB — BC 匀速移动，运动时间
为 t 秒，到达点 C 时停止，点 Q 在 AC 边上随点 P 移
动，且始终保持∠ APQ ＝∠ B .
(3)当点 P 在边 BC 上(包括端点 B )，△ APQ 为等腰三角形
时，求 PB 的长度.
1
2
解：根据题意有∠ AP为等腰三角形时，分为三种情况：
①当 AP ＝ AQ 时，∠ AQP ＝∠ APQ ＝45°，则∠ PAQ ＝
第十七章
培优拔高练

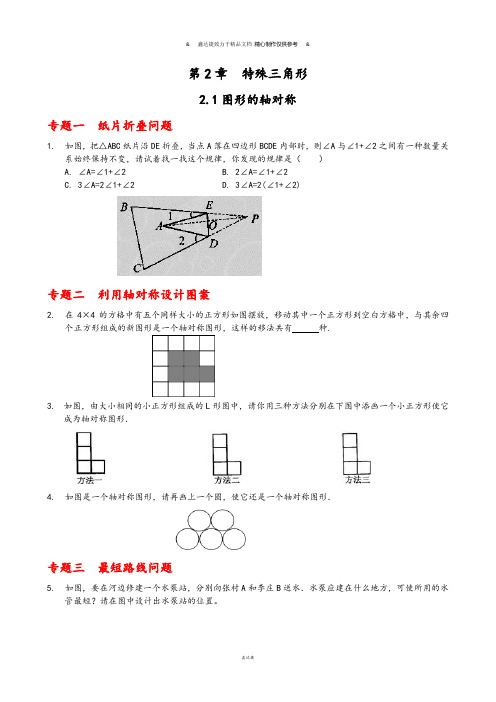
浙教版八年级数学上册2章 特殊三角形.docx

浙教版八年级数学上册2章 特殊三角形.docx

第2章特殊三角形2.1图形的轴对称专题一纸片折叠问题1. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）A. ∠A=∠1+∠2B. 2∠A=∠1+∠2C. 3∠A=2∠1+∠2D. 3∠A=2(∠1+∠2)专题二利用轴对称设计图案2. 在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种.3.如图，由大小相同的小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形．4. 如图是一个轴对称图形，请再画上一个圆，使它还是一个轴对称图形．专题三最短路线问题5. 如图，要在河边修建一个水泵站，分别向张村A和李庄B送水．水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置。

6. 如图所示，∠ABC内有一点P，在BA、BC边上各取一点P1、P2，使△PP1P2的周长最小．课时笔记【知识要点】1. 轴对称图形的概念如果把一个图形沿着一条直线折叠后，直线两侧的部分能够相互重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴.2. 轴对称图形的性质对称轴垂直平分连结两个对称点的线段.3. 图形的轴对称的概念由一个图形变为另一个图形，并使这两个图形沿某一条直线折叠后能够互相重合，这样的图形改变叫做图形的轴对称，这条直线叫做对称轴.4. 图形的轴对称的性质成轴对称的两个图形是全等图形.【温馨提示】1. 注意区分轴对称图形与图形的轴对称，轴对称图形是指一个图形具体的特性，图形的轴对称是指两个图形之间位置关系.2. 轴对称图形的对称轴至少有一条，也可以有多条.【方法技巧】1. 通过作点关于直线的对称点，利用两点之间线段最短，可作出最短路径.2. 找出对称轴是补全轴对称图形的关键，作图的依据是轴对称图形的性质.参考答案1. B 【解析】折叠前后的部分是关于直线DE对称的，即△ADE和△PDE关于直线DE对称，所以△AEO≌△PEO, △ADO≌△PDO,所以∠EAO=∠EPO, ∠DAO=∠DPO,∠2是△ADP的外角, ∠1是△EAP的外角, 所以∠1=∠EAO+∠EPO=2∠EAO, ∠2=∠DAO+∠DPO=2∠DAO,∠1+∠2=2(∠DAO+∠EAO)=2∠EAD. 所以选择B.2. 13 【解析】如图所示：一共有13种做法.3. 解：如图所示：4.解：如下图：5.解：作点A关于河边所在直线l的对称点A′，连接A′B交直线l于点P，则点P为水泵站的位置，此时PA+PB的长度之和最短，即所铺设水管最短。

第2章 特殊三角形 综合训练课件(1) 课件(浙教版八年级上)

第2章 特殊三角形 综合训练课件(1) 课件(浙教版八年级上)

• • • • •
AE CD A C AF C∴EF=DE 同理可证EF=DF ∴EF=DE=DF ∴△DEF是等边三角形
说明：证明等边三角形有三种思路： ①证明三边相等 ②证明三角相等 ③证明三角形是有一个角为 60°的等腰三角形。 具体问题中可利用不同的方式进行求 解。
A
例8：如图、在△ABC中，D，E在 直线BC上，且AB=BC=AC=CE=BD， 求∠EAC的度数。
D B C E
倍 速 课 时 学 练
探索：如图、在△ABC中，D，E 在直线BC上，且AB=AC=CE=BD， ∠DAE=100°，求∠EAC的度数。
D B
A
C
E
• • • • • • 倍 速 课 时 学 练
x
Ｄ
解：如图，令CD＝x，则AD＝x， AB＝2x ∵底边BC＝5
x
∴BC＋CD＝5＋x
Ｃ
5
AB＋AD＝3x
∴(5+x)：3x＝2:1
或3x：(5+x)=2:1
11、如图，D是正△ABC边AC上的中点，E 是BC延长线上一点，且CE=CD，诬蔑说明 BD=DE的理由. 解:∵ △ABC是正三角形 A ∴ ∠ABC= ∠ACB=600
倍 速 课 时 学 练
再 见！
倍 速 课 时 学 练
∵∠A=90°
A D
•
倍 速 课 时 学 练
•
•
∴AC= 1 DC
2 ∴AC= 1 2
B
C
BD
例4.已知：如图，∠C=90°，BC=AC，D、E分别在BC和AC上 ，且BD=CE，M是AB的中点. 求证：△MDE是等腰三角形.
• 分析：要证△MDE是等腰三角形，只需证MD=ME。连结CM，可利用 △BMD≌△CME得到结果。

最新(浙教版)八年级数学上册：单元复习(二) 特殊三角形 (共16张PPT)

最新(浙教版)八年级数学上册：单元复习(二) 特殊三角形 (共16张PPT)
拖
36 000 m ＝36 km/h＝ ＝10 m/s，∴学校受影响的时间为 120÷10 3 600 s ＝12(s)．
题组五：角平分线与全等三角形的综合应用
8．如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，
AE＝AF.求证： (1)PE＝PF；
(2)点P在∠BAC的平分线上．
③逆命题：面积相等的两个三角形全等．④逆命题：如果一个三角形
中有两个角相等，那么这个三角形是等腰三角形．(2)③的逆命题是 假命题，故③中的两个命题不是互逆定理；④中的原命题和逆命题都
是真命题，故④中的两个命题是互逆定理．
题组二：等腰三角形的性质
2．如图，在等腰三角形ABC中，AB＝AC，AD是BC边上的中线，∠ABC 的平分线BG分别交AD，AC于点E，G，EF⊥AB，垂足为点F. 求证：EF＝ED.
7．(江山市期中)如图，公路AB和公路CD交于点P，且∠APC＝30°，点Q
处有一所小学，PQ＝160 m，假设拖拉机行驶时，周围100 m以内会受到
噪声的影响，那么拖拉机在公路AB上沿PA方向行驶时，学校是否会受到 噪声影响？请说明理由；若受影响，已知拖拉机的速度为36 km/h，那
么学校受影响的时间为多少秒？
与点C的距离相等，过点D作DE⊥BC于点E.
2 2 2
3 为 s 时，线段 AP 是∠CAB 的平分线． 2 (2)因为△ACP 是以 AC 为腰的等腰三角形，当 AC＝CP＝6 时(点 P 在 BC 边上)，t1＝6÷2＝3(s)；当 AC＝CP＝6 时(点 P 在 AB 边上)，作 CD⊥AB 于点 D，图略．利用面积可求 CD＝4.8，在 Rt△PCD 中，PD＝3.6，∴ AP＝2PD＝7.2，∴t2＝(18－7.2)÷2＝5.4(s)；当 AC＝AP＝6 时，t3 ＝(18－6)÷2＝6 (s)．综上所述，当 t＝3 或 5.4 或 6 时，△ACP 是以 AC 为腰的等腰三角形．

八年级数学课件-特殊三角形

八年级数学课件-特殊三角形
说明: 因为等腰三角形的两底角相等,两个内 角的比为4:1,尚未指明哪两个角,可能是顶角 与底角的比,也可能是底角与顶角的比,所以分 两种情况求解.
此类题未说明哪两个角的比,解题时应审 清题意,注意分类讨论.
例2.如图，已知在△ABC中，AB=AC，BD⊥AC
于D，CE⊥AB于E，BD与CE相交于M点。
h
D
C
PB
h a
A M
D CQ
N
5.已知△ABC中AB=AC，AB垂直平分线交AC于E，交AB于 D，连结BE，
若∠A=50°，∠EBC=__________。
6.△ABC中，AB=AC，AD⊥BC于D，
若△ABC的周长为50，△ABD的周长为40，则 AD=____________。
7.若等腰三角形顶角为n度，则腰上的高与底边的夹角为 _____________。
等腰三角形的性质与判定
1.性质 (1)边：等腰三角形的两腰相等。 (2)角：等腰三角形的两个底角相等。(在同一个三角形中,等边对等角) (3)对称性：等腰三角形是轴对称图形,顶角平分线所在直线是它的对称轴. (4)重要线段：等腰三角形的顶角平分线、底边上的中线、底边上的高
互相重合。(等腰三角形三线合一性质)
A
• ②若BD=DC，连结AD，必有结论： ∠1=∠2，AD⊥BC1 2 • ③作AD平分∠BAC必有结论：
• AD⊥BC，BD=DC
• 作辅助线时，一定要作满足其中一个性质的辅助线，然后证出 其它两个性质，不能这样作：作AD⊥BC，使∠1=∠B2. D C
例1. 等腰三角形两个内角之比为4:1， 求顶角的度数.
A、b2=a2-c2
B、 ∠C=∠A-∠B
C、∠A：∠B：∠C=3：4：5

浙教版八年级上第二章特殊三角形复习课件

浙教版八年级上第二章特殊三角形复习课件

浙教版八年级上第二章特殊三角形复习课件一、教学内容本节课我们将复习浙教版八年级上第二章特殊三角形的内容。

具体包括：等腰三角形的性质与判定（2.1节）、等边三角形的性质与判定（2.2节）、直角三角形的性质与判定（2.3节）以及特殊三角形在实际问题中的应用（2.4节）。

二、教学目标1. 熟练掌握等腰三角形、等边三角形和直角三角形的性质与判定方法。

2. 能够运用特殊三角形的性质解决实际问题。

3. 培养学生的空间想象能力、逻辑思维能力和团队合作能力。

三、教学难点与重点教学难点：特殊三角形性质的理解与运用。

教学重点：等腰三角形、等边三角形和直角三角形的性质与判定。

四、教具与学具准备教具：多媒体课件、三角板、量角器。

学具：练习本、铅笔、直尺。

五、教学过程1. 实践情景引入（5分钟）利用多媒体课件展示特殊三角形在实际生活中的应用，如等腰三角形屋顶、等边三角形装饰等，引导学生发现生活中的特殊三角形。

2. 例题讲解（15分钟）例题1：已知△ABC中，AB=AC，∠BAC=50°，求∠ABC和∠ACB 的度数。

例题2：已知△DEF中，DE=DF=EF，求∠EDF的度数。

3. 随堂练习（10分钟）练习题1：已知△GHJ中，GH=HJ，∠G=40°，求∠J的度数。

练习题2：已知△KLM中，KL=LM=MK，求∠KLM的度数。

4. 小组讨论（5分钟）将学生分成小组，讨论特殊三角形在实际问题中的应用，如建筑、艺术等。

六、板书设计1. 等腰三角形的性质与判定2. 等边三角形的性质与判定3. 直角三角形的性质与判定4. 特殊三角形在实际问题中的应用七、作业设计1. 作业题目：（1）已知△NOP中，NO=NP，∠N=70°，求∠O和∠P的度数。

（2）已知△QRS中，QR=QS=RS，求∠QRS的度数。

（3）在生活或艺术作品中，寻找特殊三角形的应用，并说明其特点。

2. 答案：（1）∠O=∠P=55°（2）∠QRS=60°八、课后反思及拓展延伸1. 反思：本节课学生对特殊三角形的性质与判定掌握情况较好，但在实际问题中的应用方面还需加强。

河北省2024八年级数学上册第十七章特殊三角形17.4直角三角形全等的判定课件新版冀教版

BC ，∠1＝∠2.
(2)△ CDE 是不是直角三角形？并说明理由.
(2)解：△ CDE 是直角三角形，理由：
∵Rt△ ADE ≌Rt△ BEC ，
∴∠ ADE ＝∠ BEC .
又∵∠ ADE ＋∠ AED ＝90°，
∴∠ BEC ＋∠ AED ＝90°，
∴∠ DEC ＝90°，∴△ CDE 是直角三角形.
形 ABE 的高，且 AD ＝ AF ， AC ＝ AE ，
∴Rt△ ADC ≌Rt△ AFE (HL).∴ CD ＝ EF .
∵ AD ＝ AF ， AB ＝ AB ，∴Rt△ ABD ≌Rt△ ABF (HL).
∴ BD ＝ BF . ∴ BD － CD ＝ BF － EF ，即 BC ＝ BE .
BC ，∠1＝∠2.
(1)求证：Rt△ ADE ≌Rt△ BEC .
(1)证明：∵∠1＝∠2，∴ DE ＝ CE .
在Rt△ ADE 和Rt△ BEC 中，
＝，
∵ቊ
＝，
∴Rt△ ADE ≌Rt△ BEC (HL).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. 如图，∠ A ＝∠ B ＝90°， E 是 AB 上的一点，且 AE ＝
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点2
尺规作直角三角形
8. [教材P159例1变式]如图，已知线段 a ， b ，其中 a ＞ b ，求
作直角三角形 ABC ，使得∠ C 为直角， AB ＝ a ， AC ＝

冀教版初中数学八年级上册特殊三角形复习精品课件PPT


冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
已知：如图，∠A=90°，∠B=15°，BD=DC. 请说明AC=BD的理由.
A D
B
C
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
例5、如图，已知四边形ABCD中，∠B=90°AB=4， BC=3,AD=12，DC=13 ，求四边形ABCD的面积 D
A
BC
例6、如图已知四边形ABCD中，∠A=60°∠B=∠D=9 BC=3，CD=2，求AB2的值 A
D
B
C
E
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
特殊三角形的性质与判定
1.性质 (1)：等腰三角形的两个底角相等。 (2)：等腰三角形的顶角平分线、底边上的中线、 底边上的高互相重合。
2.判定 定义：有两边相等的三角形是等腰三角形。 判定定理：有两个角相等的三角形是等腰三角 形。 等腰三角形:
2x
Ｄ
∵底边BC＝5
x
∴BC＋CD＝5＋x
Ｂ
5
Ｃ AB＋AD＝3x ∴(5+x)：3x＝2:1
或3x：(5+x)=2:1
冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件
例4、如图，已知AB=AD，CB=CD，AC，BD相交于 冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件 点O，若AB=5，AC=7，BD=6,求∠BCD的度数

河北省2024八年级数学上册第十七章特殊三角形17.2直角三角形课件新版冀教版

AD ⊥ AB ，点 E 是 BD 的中点，连接 AE .
(1)求证：∠ AEC ＝∠ C ；
证明：(1)∵ AD ⊥ AB ，
∴△ ABD 为直角三角形.
又∵点 E 是 BD 的中点，

∴ AE ＝ BE ＝ BD ，

∴∠ B ＝∠ BAE .
∵∠ AEC ＝∠ B ＋∠ BAE ，
∴∠ AEC ＝∠ B ＋∠ B ＝2∠ B .
∴ AE ＝ AC .




又∵ AE ＝ BD ，∴ AC ＝ BD ，∴ BD ＝2 AC .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. 【学科素养·推理能力】[2023邢台任泽区月考]如图，在
Rt△ ABC 中，∠ ACB ＝90°，∠ A ＝30°， BC ＝2.三
角尺中30°角的顶点 D 在边 AB 上，两边分别与△ ABC
A. 6
B. 7
1
2
3
4
5
C. 8
6
7
8
9
10
11
12
D )
D. 9
13
14
15
16
10. [2024张家口万全区期末]如图，在△ ABC 中，∠ C ＝
90°，∠ ABC ＝60°， BD 平分∠ ABC ，若 AD ＝6，则
CD ＝
3
1
2
.
⁠
3
4
5
6
7
8
9
10
11
12
13
14

冀教版初中数学八年级上册 特殊三角形复习 课件示范


t3=
5 2
My idea
本节课， 你有怎样的思考、收获和感受呢？
My idea
1.化动为静 2.分类讨论 3.构造基本图形 4.建立方程
6
8
2t 2t
设运动时间为t 秒 ,则AD=2t，BD=10-2t. (1)当t为何值时，△ACD为直角三角形， 请求出所有t的值？
6？
8
2t 2t
设运动时间为t 秒 ,则AD=2t，BD=10-2t.
角不明确(顶角、底角) 三角形类型不明确 腰上高线(内、外、上)
分类讨论 腰上中线分周长(上、下) 三角形顶角顶点不明确
直角 三角形
边不明确(直角边、斜边) 直角不明确(三种可能)
验收成果3
6
8
如图，在Rt△ABC中,∠C=90°,动 点D沿着AB, 从点A匀速运动到终点B 停止. 若AC=6cm, BC=8cm, 点D的运动 速度为每秒钟2cm,设运动时间为t 秒.
60°角
等腰三角形 ——→ 等边三角形
底=腰
B
B C
旧知识 新视角
等腰三角形 A
直角三角形 A
C
B B C
B
验收成果1
1.如图,在△ABC中,AB=AC ,AD平分
∠BAC．已知AB=5 , AD=3 ,
则BC长为（ C ）
A．5 B．6
C．8 D．10
A
53
C
D
B
验收成果1
2.如图，在△ABC中, AD是BC边上 的中线, BC=6 , AD=4 , AB=5 . 求证: AB=AC A
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。 6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。 7.阅历之所以会对读书所得产生深浅 有别的 影响， 原因在 于阅读 并非是 对作品 的简单 再现， 而是一 个积极 主动的 再创造 过程， 人生的 经历与 生活的 经验都 会参与 进来。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三角形难题集锦
1. 如图，在△ABC中，AB=BC，在BC上取点M，在MC 上取点N，使MN=NA，若∠BAM=
∠NAC，则∠MAC= 度。

第1题
2. 如图，等腰直角三角形ABC直角边长为1，以它的斜边上的高AD为腰作第一个等腰直
上的高AF为
腰作第二个角三角形ADE，再以所作的第一个等腰直角三角形ADE的斜边
为。

等腰直角三角形AFG；⋯⋯以此类推，这
样所作的第n 个等腰直角三角形的腰长
3、如图，在三角形ABC中，AB=5，AC=13，边B C上的中线A D=6，则B C的长为
4、如图，在△ABC中，∠ABC=100o，AM=AN,CN=CP求, ∠MNP的度数
5、如图：△ABC中，AD是角平分线，AD=BD，AB=2AC。

求证：△ACB是直角三角形。

A
C D B
2 6、如图，在三角形ABC 中，AB=AC=5，P 是BC 边上除B、C 点外的任意一点，则AP
+PB·PC= 。

7、如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB 于E，并且AE=0.5（AB+AD），则∠ABC+∠ADC的度数是度。

8、如图，AM、BN 分别是∠EAB、∠DBC的平分线，若AM=BN=AB，则∠BAC的度数为------------ 度。

9、如图，AE、AD 是直线且AB=BC=CD=DE=EF=FG=G，A若∠DAE=x°,求x 的度数
10、如图，已知△ABC是等边三角形，∠BDC＝120o，说明AD=BD+CD的理由
11、如图5，在△ABC中，BC>AC，点D在BC上，且D C＝AC,∠ACB的平分线CF交AD于F，点E 是AB的中点，连结EF.
（1）求证：EF∥BC.
（2）若四边形BDFE的面积为6，求△ABD的面积.
12 两个全等的含30 度、60 度角的三角板ADE和三角板ABC，如图所示放置，E、A、C 三点在一条直线上，边结 B D，取BD 的中点M ，连结ME、MC，试判断△EMC 的形状，并说明理由。

13、如图，已知在△ABC中，AD 是BC边上的中线，E是AD 上一点，且BE=AC，延长BE交AC于F，求证：AF=EF
14、如图，等边△ABC中，延长BC到Ｄ，延长ＢＡ到Ｅ，使AE＝B D，连CE，DE，求证：CE=DE。

15、在Rt△ABC中，∠ACB=90，C D⊥AB 于D，设AC=b,BC=a,AB=c,CD=h.
求证: (1)
(2) a+b<c+h
(3) 以a+b、h、c+h 为边的三角形，是直角三角形。