相似三角形典型例题

.\1：相像三角形模型一：相像三角形判断的基本模型（一） A 字型、反 A 字型（斜 A 字型）AADD E EB C B C（平行）（不平行）（二） 8 字型、反 8 字型AA BBO JC DC D（蝴蝶型）（平行）（不平行）（三）母子型AADDB C C（四）一线三等角型：三等角型相像三角形是以等腰三角形（等腰梯形）或许等边三角形为背景，一个与等腰三角形的底角相等的极点在底边所在的直线上，角的两边分别与等腰三角形的两边订交以下图：.\（五）一线三直角型：三直角相像能够看着是“一线三等角”中当角为直角时的特例，三直角型相像往常是以矩形或许正方形形为背景，或许在一条直线上有一个极点在该直线上挪动或许旋转的直角，几种常有的基本图形以下：当题目的条件中只有一个或许两个直角时，就要考虑经过增添协助线结构完好的三直角型相像，这常常是好多压轴题的打破口，从而将三角型的条件进行转变。

（六）双垂型：ADC二：相像三角形判断的变化模型旋转型：由 A 字型旋转获得AD EB C8 字型拓展AE FGB C 共享性一线三等角的变形.\一线三直角的变形2：相像三角形典型例题（ 1）母子型相像三角形例 1：如图，梯形ABCD 中， AD ∥ BC，对角线 AC、 BD 交于点 O， BE∥ CD 交 CA 延伸线于E．求证： OC2OA OE ．例 2：已知：如图，△ABC中，点E在中线AD上,D EB ABC ．求证：（ 1）DB2DE DA ；（2）DCE DAC ．BDEA C例 3：已知：如图，等腰△ABC中，AB＝AC，AD⊥ BC于D，CG∥ AB，BG分别交AD、AC于E、F．求证： BE2EF EG ．1、如图，已知AD 为△ABC 的角均分线， EF 为 AD 的垂直均分线．求证：FD 2FB FC ．2、已知： AD 是 Rt△ABC 中∠ A 的均分线，∠ C=90°，EF 是 AD 的垂直均分线交AD 于 M ，EF、BC 的延.\长线交于一点N。

九年级数学相似三角形典型例题一、利用相似三角形的判定定理证明相似例1：已知：在△ABC和△DEF中，∠A = ∠D = 60°，AB = 4，AC = 8，DE = 2，DF = 4。

求证：△ABC∽△DEF。

解析：1. 我们看相似三角形的判定定理。

对于两个三角形，如果它们的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

2. 在本题中：计算公式，公式。

并且已知∠A = ∠D = 60°。

因为公式且∠A = ∠D，所以根据相似三角形判定定理中的“两边对应成比例且夹角相等的两个三角形相似”，可以得出△ABC∽△DEF。

二、相似三角形性质的应用（求边长）例2：已知△ABC∽△A'B'C'，相似比为公式，若AB = 6，则A'B'的长为多少？解析：1. 因为相似三角形对应边成比例。

设A'B' = 公式。

已知相似比公式。

2. 又已知公式，AB = 6，所以公式。

通过交叉相乘可得：公式。

即公式，解得公式，所以A'B'的长为9。

三、利用相似三角形解决实际问题（测量高度）例3：在同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，求这棵大树的高度。

解析：1. 因为在同一时刻，太阳光下不同物体的高度和影长成正比。

设大树的高度为公式米。

可以得到两个相似三角形，一个是由小强及其影子构成，另一个是由大树及其影子构成。

2. 根据相似三角形的性质，对应边成比例。

则公式。

交叉相乘可得：公式。

计算得公式，解得公式米。

所以这棵大树的高度是9.6米。

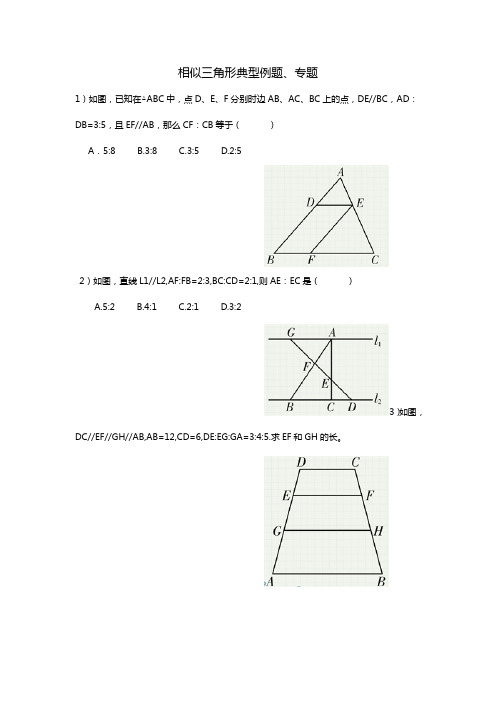
相似三角形典型例题、专题1）如图，已知在△ABC中，点D、E、F分别时边AB、AC、BC上的点，DE//BC，AD：DB=3:5，且EF//AB，那么CF：CB等于（）A．5:8 B.3:8 C.3:5 D.2:52）如图，直线L1//L2,AF:FB=2:3,BC:CD=2:1,则AE：EC是（）A.5:2B.4:1C.2:1D.3:23）如图，DC//EF//GH//AB,AB=12,CD=6,DE:EG:GA=3:4:5.求EF和GH的长。

4）如图所示，AE=2EC,AH=2HD,BG=2GC,BF=2FD,连接EF,GH相交于点O。

求证：GH 与EF互相平分。

5）已知：P为△ABC的中位线MN上任意一点，BP、CP的延长线分别交对边AC、AB于D、E，求证：AD/DC+AE/EB=1.6)下列四个命题中，假命题是（）A.有一个锐角相等的两个等腰三角形相似B.有一个锐角相等的两个直角三角形相似C.底边和腰对应成比例的两个等腰三角形相似D.斜边和直角边对应成比例的两个直角三角形相似7）如图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC相似的是（）8）如图，一张等腰直角三角形纸片，底边长12cm，底边上的高12cm，现沿底边依次从下往上裁剪宽度为2cm的矩形纸条，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（）A．第4张 B.第5张 C.第6张 D.第7张9）如图，P是△ABC内一点，过P分别作直线平行于△ABC的各边，所成的小三角形t1、t2、t3的面积分别是4、9、49.则S△ABC=______________.10）将△ABC的纸片按如图所示的方式折叠，使点B落在边AC上，记为点B`,折痕为EF，已知AB =AC=8，BC=10，若以点B`、F、C为顶点的三角形与△ABC相似，那么BF的长度为_______________.11)如图，在△ABC中，D是BC边的中点，DE⊥BC交AB于点E，AD=AC，EC交AD于点F.求证：FC=3EF.12）如图，E、F分别是平行四边形ABCD边BC、CD的中点，AE、AF交BD于点G、H，若△AGH的面积为1，则五边形CEGHF的面积是（）A. 1B. 2C. 3D. 413）已知△ABC中，AB=AC=m,∠ABC=72°,BB₁平分∠ABC交AC于B₁,过B₁作B1B2//BC 交AB于B2，作B2B3平分∠AB2B1，交AC于B3过B3作B3B4//BC，交AB于B4……依次进行下去，则B9B10线段的长度用含有m的代数式可以表示为__________________.14）如图，四边形ABCD是梯形，点E是上底边AD上一点，CE的延长线于BA的延长线交于点F，过点E作BA的平行线交CD的延长线于点M，BM与AD交于点N。

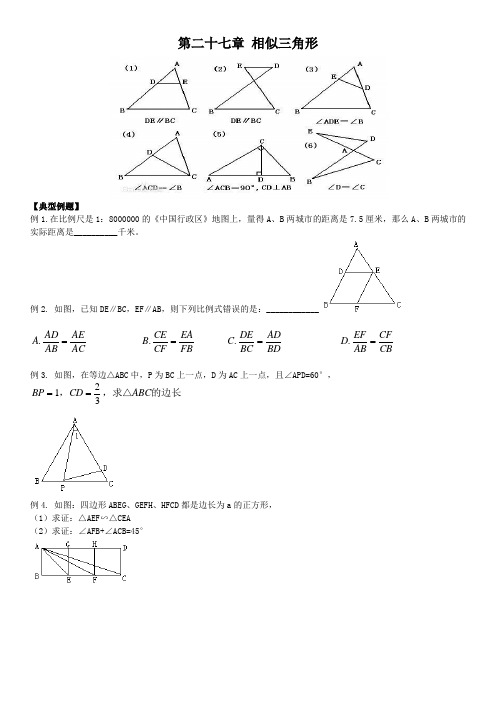
第二十七章 相似三角形 【典型例题】 例1.在比例尺是1：8000000的《中国行政区》地图上，量得A、B两城市的距离是7.5厘米，那么A、B两城市的实际距离是__________千米。

例2. 如图，已知DE∥BC，EF∥AB，则下列比例式错误的是：____________

AADABAEACBCECFEAFB.. CDEBCADBDDEFABCFCB..

例3. 如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD=60°， BPCDABC123，，求△的边长

例4. 如图：四边形ABEG、GEFH、HFCD都是边长为a的正方形， （1）求证：△AEF∽△CEA （2）求证：∠AFB+∠ACB=45° 例5. 已知：如图，梯形ABCD中，AD∥BC，AC、BD交于点O，EF经过点O且和两底平行，交AB于E，交CD于F 求证：OE=OF

例6. 如图，D为△ABC中BC边上的一点，∠CAD=∠B，若AD=6，AB=8，BC=16，求AC的长。 例7、如图10，四边形ABCD、DEFG都是正方形，连接AE、CG,AE与CG相交于点M，CG与AD相交于点N． 求证：（1）； （2）

例8. 如图，在矩形ABCD中，E是CD的中点，BE⊥AC于F，过F作FG∥AB交AE于G， 求证：AG2=AF·FC

例9、如图10所示，E是正方形ABCD的边AB上的动点， EF⊥DE交BC于点F． （1）求证： ADE∽BEF； （2）设正方形的边长为4， AE=，BF=．当取什么值时， 有最大值?并求出这个最大值．

CGAE.MNCNDNAN

xyxy训练 1、如图AB∥CD∥EF，则图中相似三角形的对数为（ ） A、 1对 B、 2对 C、 3对 D、 4对 2、如图，DE与BC不平行，当ACAB= 时， ΔABC与ΔADE相似。 3、如图，AB⊥BC，DC⊥BC，垂足分别为B、C，且AB=8，DC=6，BC=14，BC上是否存在点P使△ABP与△DCP相似？若有，有几个？ 并求出此时BP的长，若没有，请说明理由。

1：类似三角形模子一：类似三角形剖断的根本模子（一）A字型.反A字型（斜A字型）（平行）（不服行）（二）8字型.反8字型（平行）（不服行）（三）母子型（四）一线三等角型：三等角型类似三角形是以等腰三角形（等腰梯形）或者等边三角形为布景,一个与等腰三角形的底角相等的极点在底边地点的直线上,角的双方分离与等腰三角形的双方订交如图所示：（五）一线三直角型：三直角类似可以看着是“一线三等角”中当角为直角时的特例,三直角型类似平日是以矩形或者正方形形为布景,或者在一条直线上有一个极点在该直线上移动或者扭转的直角,几种罕有的根本图形如下：当标题标前提中只有一个或者两个直角时,就要斟酌经由过程添加帮助线结构完全的三直角型类似,这往往是许多压轴题的冲破口,进而将三角型的前提进行转化.（六）双垂型：二：类似三角形剖断的变更模子扭转型：由A字型扭转得到8字型拓展CB EDA共享性一线三等角的变形2：类似三角形典范例题（1）母子型类似三角形例1：如图,梯形ABCD中,AD∥BC,对角线AC.BD交于点O,BE∥CD交CA延伸线于E．求证：OEOAOC⋅=2．GAB CE F例2：已知：如图,△ABC 中,点E 在中线AD 上求证：（1（2例3：已知：如图,等腰△ABC 中,AB ＝AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分离交AD .AC 于E .F ．1.如图,已知AD 为△ABC 的角等分线,EF 为AD的垂直等分线．求证：2.已知：AD 是Rt△ABC 中∠A 的等分线,∠C=90°,EF 是AD 的垂直等分线交AD 于M,EF.BC 的延伸线交于一点N.求证：(1)△AME∽△NMD;3.已知：如图,在△ABC 中,∠ACB=90°,CD⊥AB 于D,E 是AC 上一点,CF ⊥BE 于F.求证：EB·DF=AE·DB4.,AB=AC,高AD与BE 交于垂足为F,延伸AD 到G,使DG=EF,M 是AH的中点.5已知：如图,在Rt△ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D （点D 与点A .C 都不重合）,E 是射线DC 上一点,且∠EPD =∠A ．设A .P 两点的距离为x ,△BEP 的面积为y ．（1）求证：AE =2PE ;（2）求y 关于x 的函数解析式,并写出它的界说域; （3）当△BEP 与△ABC 类似时,求△BEP 的面积．AD EB（2）双垂型1.如图,在△ABC中,∠A=60°,BD.CE分离是AC.AB上的高求证：（1）△ABD∽△ACE;（2）△ADE∽△ABC;(3)BC=2ED2.如图,已知锐角△ABC,AD.CE分离是BC.AB边上的高,△ABC和△BDE的面积分离是27和求：点B到直线AC的距离.（3）共享型类似三角形1.△ABC是等边三角形,DBCE在一条直线上,∠DAE=120°,已知BD=1,CE=3,求等边三角形的边长.2.已知：如图,在Rt△ABC中,AB=AC,∠DAE=45°．求证：（1）△ABE∽△ACD; （2(4)一线三等角型类似三角形例1：如图,等边△ABC中,边长为6,D是BC上动点,∠EDF=60°（1）求证：△BDE∽△CFD（2）当BD=1,FC=3时,求BE例2：（1）,,;,并写出函数的界说域;D ECADBE F（2）,,,.例3：已知在梯形ABCD 中,AD ∥BC ,AD ＜BC ,且AD ＝5,AB ＝DC ＝2． （1）如图8,P 为AD 上的一点,知足∠BPC ＝∠A ．①求证;△ABP ∽△DPC ②求AP 的长．（2）假如点P 在AD 边上移动（点P 与点A .D 不重合）,且知足∠BPE ＝∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在DC 的延伸线上时,设AP ＝x ,CQ ＝y ,求y 关于x 的函数解析式,并写出函数的界说域;②当CE ＝1时,写出AP 的长．例4：如图,的中点,ABC PQAB CDCAB CDABC（1（2,; （31.如图,在△ABC 中,边上, (1) 求证：△ABD ∽△DCE;(2),; (3),试解释△ADE 是什么三角形,并解释来由．2.如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,联络DE,射线EF 交线段AC 于F ． （1）求证：△DBE ∽△ECF ;（2）当F 是线段AC 中点时,求线段BE 的长;（3）联络DF ,假如△DEF 与△DBE 类似,求FC 的长．3.已知在梯形ABCD 中,AD ∥BC ,AD ＜BC ,且BC =6,AB =DC =4,点E 是AB 的中点．（1）如图,P 为BC 上的一点,且BP =2．求证：△BEP ∽△CPD ;（2）假如点P 在BC 边上移动（点P 与点B .C 不重合）,且知足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么①当点F 在线段CD的延伸线上时,设BPDF,并写出函数的界说域;ABCDE,求BP的长．4.如图,动点,（1; （2）证实个中一对三角形类似;（3,; （4(5)一线三直角型类似三角形例1.已知矩形ABCD 中,CD=2,AD=3,点P 是AD 上的一个动点,且和点A,D 不重合,过点P 交边AB 于点E,求y 关于x 的函数关系式,并写出x 的取值规模. 例2.AB 上的一点,点P 是AC上的一个动点段BC 于点Q,（不与点B,C 重合）,x 的函数关系,并写出界说域. 1.点D 是BC 的中点,点E 是AB 边上的动点AC 于点F （1）.求AC 和BC 的长EDCBAPB（2）.,求BE 的长.（3）.贯穿连接EF,,求BE的长.2.在直角三角形ABC 中是AB 边上的一点,E 是在AC 边上的一个动点,（与A,C 不重合）BC 订交于点F.(1).当点D 是边AB 的中点时,(2).（3）.求y 关于x 的函数关系式,并写出界说域3.如图,的一个动点,（1,;（2,. 4.如图,(图1) (1); (2),;(图2)(3),并写出界说域.F CBAQPDCBAQPDC BA。

AD E MC FA D C BB 《相似三角形的性质》典型例题例1：（2002江苏南通）已知：AD:AB=1:3 DE ∥ BC 则S △ADE :S △AB =______ 分析：本题是考查相似三角形的性质，由于相似三角形面积的比等于相似比的平方，所以只要能得到△ADE ∽△ABC,那么S △ADE: S △ABC 的植即可求出，故S △ADE: : S△ABC=AD 2:AB 2=1:9例2：已知如图，在△ABC 中，D 是AB 上一点，43==BC BD AB BC ，△BCD 的周长是24cm ，求⑴△ABC 的周长⑵S △BCD:S △ ACD = ⑶若CD =12cm,求AC解：⑴∵,43==BC BD AB BC 公共，∴△BCD ∽△BAC ∴34==BC AB BCD ABC 的周长的周长▲▲ 已知△BCD 的周长为24cm,∴△ABC 之周长=24×34=32(cm) ⑵∵9163422▲▲=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=BC AB S S BCD ABC 而S △ACD =S △ABC －S △BCD∴979916▲▲▲▲▲=-==-BCD BCD ABC BCD ACD S S S S S ∴79▲▲=ACD BCD S S (3)∵△BAC ∽△BCD ∴BDBCCD AC = ∵CD=12cm ∴AC=CD ×BD BC =12×34=16（cm ）例3：在△ABC 中，D 为AB 之中点，DE 的延长线交BC 延长线于F ， 求证：AE ·CF=BF ·EC分析：要证AE ·ＣＥ＝ＢＦ·ＣＦ，就要证CFBFCE AE =，可是题目中既没有平行线，而四条线段ＡＥ、CE 、 BF 、CF 又不同在两个三角形中，因此设法作辅助线，寻找中间比，实现比的过渡，以达到解题目的。

故过点C 作AB 的平行线。

解：过C 作CM ∥AB 交 EF 于M ，易得△ADE ∽△CME ，△CFM ∽△BFD ，∴CM ADCE AE =，∴CM BD CF BF =，又BD=AD ∴CF BF CE AE =小结：本题通过作平行线，得到两对相似三角形，两个比例式， 实现比的过渡，B P CED同学们要掌握这一技巧。