第一讲实数实函数
- 格式:doc
- 大小:862.00 KB
- 文档页数:12




第一章 实数集与函数(10学时)§1.实数教学目的:使学生把握实数的大体性质.教学重点:(1)明白得并熟练运用实数的有序性、浓密性和封锁性;(2)牢记并熟练运用实数绝对值的有关性质和几个常见的不等式.(它们是分析论证的重要工具) 教学难点:实数集的概念及其应用.学时安排: 2学时教学方式:教学.(部份内容自学)教学程序:引言上节课中,咱们与大伙儿一起探讨了《分析》这门旅程的研究对象、要紧内容等话题.从本节课开始,咱们就大体依照教材顺序给大伙儿介绍这门课程的要紧内容.第一,从大伙儿都较为熟悉的实数和函数开始.[问题] 什么缘故从“实数”开始.答:《数学分析》研究的大体对象是函数,但那个地址的“函数”是概念在“实数集”上的(《复变函数》研究的是概念在复数集上的函数).为此,咱们要先了解一下实数的有关性质.一 实数及其性质 1、实数(,q p q p ⎧⎧≠⎪⎨⎨⎩⎪⎩正分数,有理数为整数且q 0)或有限小数和无限小数.负分数,无理数:用无限不循环小数表示. {}|R x x =--为实数全体实数的集合.[问题] 有理数,无理数的表示不统一,这对统一讨论实数是不利的.为以下讨论的需要,咱们把“有限小数”(包括整数)也表示为“无穷小数”.为此作如下规定: ,n a 其,,n n a ≠19999n a -;关于正整数0,x a =1).9999;关于负有限小数(包括负整,那么先将y -表示为无穷小数,此刻所得的小数之前加负号.0=0.0000例:2.001 2.0009999→3 2.99992.001 2.0099993 2.9999→-→--→-利用上述规定,任何实数都可用一个确信的无穷小数来表示.但新的问题又显现了:在此规定下,如何比较实数的大小?2.两实数大小的比较1) 概念1 给定两个非负实数01n x a a a =,01n y b b b =. 其中00,a b 为非负整数,,k k a b (1,2,)k =为整数,09,09k k a b ≤≤≤≤.假设有,1,2,k k a b k ==,那么称x 与y 相等,记为x y =;假设00a b >或存在非负整数l ,使得,1,2,,k k a b k l ==,而11l l a b ++>,那么称x 大于y 或y 小于x ,别离记为x y >或y x <.关于负实数x 、y ,假设按上述规定别离有x y -=-或x y ->-,那么别离称为x y =与x y <(或y x >).规定:任何非负实数大于任何负实数.2) 实数比较大小的等价条件(通过有限小数来比较).概念2(不足近似与多余近似):01n x a a a =为非负实数,称有理数01n x a a a =为实数x 的n 位不足近似;110n n n x x =+称为实数x 的n 位多余近似;关于实数01nx a a a =-,其n 位不足近似01110n n n x a a a =--;n 位多余近似01n n x a a a =-. 注:实数x 的不足近似n x 当n 增大时不减,即有012;x x x x ≤≤≤≤ 多余近似n x 当n 增大时不增,即有01x x x x ≥≥≥≥.命题:记01n x a a a =,01n y b b b =为两个实数,那么x y >的等价条件是:存在非负整数n ,使n n x y >(其中n x 为x 的n 位不足近似,n y 为y 的n 位多余近似).命题应用————例1例1.设,x y 为实数,x y <,证明存在有理数r ,知足x r y <<.证.由x y <,知:存在非负整数n ,使得n n x y <.令()12n n r x y =+,那么r 为有理数,且 n n x x r y y ≤<<≤.即x r y <<.3.实数经常使用性质(详见附录Ⅱ.P289-302).● 封锁性(实数集R对,,,+-⨯÷)四那么运算是封锁的.即任意两个实数的和、差、积、商(除数不为0)仍是实数.● 有序性:任意两个实数,a b 必知足以下关系之一:,,a b a b a b <>=.● 传递性;,a b b c a c <>⇒>.● 阿基米德性:,,0a b R b a n N ∀∈>>⇒∃∈使得na b >.● 浓密性:两个不等的实数之间总有另一个实数.● 实数集R与数轴上的点有着一一对应关系.例2.设,a b R ∀∈,证明:假设对任何正数ε,有a b ε<+,那么a b ≤.(提示:反证法.利用“有序性”,取a b ε=-)二 、绝对值与不等式(分析论证的大体工具).1.绝对值的概念实数a 的绝对值的概念为,0||0a a a a a ≥⎧=⎨-<⎩.2. 几何意义:从数轴看,数a 的绝对值||a 确实是点a 到原点的距离.熟悉到这一点超级有效,与此相应,||x a - 表示确实是数轴上点x 与a 之间的距离.3.性质.1)||||0;||00a a a a =-≥=⇔=(非负性);2)||||a a a -≤≤;3)||a h h a h <⇔-<<,||.(0)a h h a h h ≤⇔-≤≤>;4)对任何,a b R ∈有||||||||||a b a b a b -≤±≤+(三角不等式);5)||||||ab a b =⋅;6)||||a a b b =(0b ≠). [练习]P4. 5[课堂小结]:实数:⎧⎨⎩一 实数及其性质二 绝对值与不等式.§2数集和确界原理教学目的:使学生把握确界原理,成立起实数确界的清楚概念。


实函数知识点总结实函数是数学中非常基础且重要的概念,它在微积分、数学分析、代数、几何等许多数学领域都有重要的应用。
因此,对实函数的理解和掌握对于学生来说非常关键。
本文将从实函数的基本概念、性质、极限、导数、积分等方面进行详细的总结和介绍。
一、实函数的基本概念1. 实函数的定义实函数是指定义在实数集上的函数,通常表示为f(x),其中x为定义域上的实数。
实函数可以用图像表示,在平面直角坐标系中,实函数的图像通常是一条曲线。
2. 实函数的定义域和值域实函数的定义域是指函数定义的所有实数的集合,通常表示为D(f)。
而值域是指函数在定义域上取得的所有实数的集合,通常表示为R(f)。
3. 实函数的奇偶性实函数的奇偶性是指函数的对称性。
如果f(-x) = f(x),则函数f(x)是偶函数;如果f(-x) = -f(x),则函数f(x)是奇函数;如果函数既不是偶函数也不是奇函数,则为非奇非偶函数。
4. 实函数的周期性实函数的周期性是指函数在定义域上具有重复性。
如果存在一个正数T,使得对于定义域上的所有x都有f(x+T) = f(x),则函数f(x)是周期函数,T称为函数f(x)的周期。
二、实函数的性质1. 实函数的有界性如果存在正数M,使得对于定义域上的所有x都有|f(x)| ≤ M,则函数f(x)在定义域上有上界M和下界-M,即函数f(x)是有界的。
2. 实函数的单调性如果对于定义域上的任意两个实数x1和x2,当x1 < x2时有f(x1) ≤ f(x2),则函数f(x)是递增函数;如果对于定义域上的任意两个实数x1和x2,当x1 < x2时有f(x1) ≥ f(x2),则函数f(x)是递减函数。
3. 实函数的周期性如果存在一个正数T,使得对于定义域上的所有x都有f(x+T) = f(x),则函数f(x)是周期函数,T称为函数f(x)的周期。
4. 实函数的复合函数如果存在两个函数f(x)和g(x),则函数F(x) = f(g(x))称为复合函数。

秋风清,秋月明,落叶聚还散,寒鸦栖复惊。
授课章节:第一章 实数集与函数---§1.实数教学目的:使学生掌握实数的基本性质.教学重点:(1)理解并熟练运用实数的有序性、稠密性和封闭性;(2)牢记并熟练运用实数绝对值的有关性质以及几个常见的不等式.(它们是分析论证的重要工具)教学难点:实数集的概念及其应用.教学方法:讲授.(部分内容自学)教学程序:引言上节课中,我们与大家共同探讨了《分析》这门旅程的研究对象、主要内容等话题.从本节课开始,我们就基本按照教材顺序给大家介绍这门课程的主要内容.首先,从大家都较为熟悉的实数和函数开始.[问题] 为什么从“实数”开始.答:《数学分析》研究的基本对象是函数,但这里的“函数”是定义在“实数集”上的(《复变函数》研究的是定义在复数集上的函数).为此,我们要先了解一下实数的有关性质.一 实数及其性质 1、实数(,q p q p⎧⎧≠⎪⎨⎨⎩⎪⎩正分数,有理数为整数且q 0)或有限小数和无限小数.负分数,无理数:用无限不循环小数表示. {}|R x x =--为实数全体实数的集合.[问题] 有理数,无理数的表示不统一,这对统一讨论实数是不利的.为以下讨论的需要,我们把“有限小数”(包括整数)也表示为“无限小数”.为此作如下规定:例:2.001 2.0009999→3 2.99992.001 2.0099993 2.9999→-→--→-利用上述规定,任何实数都可用一个确定的无限小数来表示.但新的问题又出现了:在此规定下,如何比较实数的大小?2.两实数大小的比较1) 定义1 给定两个非负实数01n x a a a = ,01n y b b b = . 其中00,a b 为非负整数,,k k a b (1,2,)k = 为整数,09,09k k a b ≤≤≤≤.若有,1,2,k k a b k == ,则称x 与y 相等,记为x y =;若00a b >或存在非负整数l ,使得,1,2,,k k a b k l == ,而11l l a b ++>,则称x 大于y 或y 小于x ,分别记为x y >或y x <.对于负实数x 、y ,若按上述规定分别有x y -=-或x y ->-,则分别称为x y =与x y <(或y x >).规定:任何非负实数大于任何负实数.2) 实数比较大小的等价条件(通过有限小数来比较).定义2(不足近似与过剩近似):01n x a a a = 为非负实数,称有理数01n x a a a = 为实数x 的n 位不足近似;110n n nx x =+称为实数x 的n 位过剩近似;对于实数01n x a a a =- ,其n 位不足近似01110n n n x a a a =-- ;n 位过剩近似01n n x a a a =- . 注:实数x 的不足近似n x 当n 增大时不减,即有012;x x x x ≤≤≤≤ 过剩近似n x 当n 增大时不增,即有01x x x x ≥≥≥≥ .命题:记01n x a a a = ,01n y b b b = 为两个实数,则x y >的等价条件是:存在非负整数n ,使n n x y >(其中n x 为x 的n 位不足近似,n y 为y 的n 位过剩近似). 命题应用————例1例1.设,x y 为实x y <,证明存在有理数r ,满足x r y <<.证.由x y <,知:存在非负整数n ,使得n n x y <.令()12n n r x y =+,则r 为有理数,且 n n x x r y y ≤<<≤.即x r y <<.3.实数常用性质(详见附录Ⅱ.P289-302).● 封闭性(实数集R对,,,+-⨯÷)四则运算是封闭的.即任意两个实数的和、差、积、商(除数不为0)仍是实数.● 有序性:任意两个实数,a b 必满足下列关系之一:,,a b a b a b <>=.● 传递性;,a b b c a c <>⇒>.● 阿基米德性:,,0a b R b a n N ∀∈>>⇒∃∈使得na b >.● 稠密性:两个不等的实数之间总有另一个实数.● 实数集R与数轴上的点有着一一对应关系.例2.设,a b R ∀∈,证明:若对任何正数ε,有a b ε<+,则a b ≤.(提示:反证法.利用“有序性”,取a b ε=-)二 、绝对值与不等式(分析论证的基本工具).1.绝对值的定义实数a 的绝对值的定义为,0||0a a a a a ≥⎧=⎨-<⎩.2. 几何意义:从数轴看,数a 的绝对值||a 就是点a 到原点的距离.认识到这一点非常有用,与此相应,||x a - 表示就是数轴上点x 与a 之间的距离.3.性质.1)||||0;||00a a a a =-≥=⇔=(非负性);2)||||a a a -≤≤;3)||a h h a h <⇔-<<,||.(0)a h h a h h ≤⇔-≤≤>;4)对任何,a b R ∈有||||||||||a b a b a b -≤±≤+(三角不等式);5)||||||ab a b =⋅;6)||||a a b b =(0b ≠). [练习]P4. 5[课堂小结]:实数:⎧⎨⎩一 实数及其性质二 绝对值与不等式.[作业]P4.1.(1) 2.(2)、(3) 3。



第一讲实数与实函数1 . 1 实数与实函数的基本概念一.实数实数包括有理数和无理数.有理数,就是能够表示成qp形式的数,其中 p 是整数, q 是不为零的整数.如果用小数表示,有理数都可以表示成有限小数,或无限循环小数.无理数,就是不能表示成qp形式的数,也就是无限不循环的小数.如果将有限小数也表示成无限小数,例如:数 1 可表示为 1=1.000… ;也可以表示为 l=0.999… (注:这是实无限的观点),为唯一性起见,数学上作了一个约定,就是不以零为循环节.数 1 约定的表示为l=0.999…,因此,实数就是一个可以用无限小数表示的数.二、实数的性质1 .实数集合 R 是一个阿基米德有序域( 1 )在实数集合 R 上定义加法“ + ”和乘法“× ”两种运算,对两种运算分别满足交换律、结合律,以及乘法关于加法的分配律;对加法,有“零元”和“负元”;对乘法有“单位元”和“逆元” ; R 成为一个“域”.( 2 )在集合 R 上定义了一种序关系“ < " ,且满足传递性:即对 R c b a ∈∀,, ,若 a < b , b < c ,则 a <c ;三歧性:即对 ,,R b a ∈∀,关系 a < b , a =b , a > b 三者必居其一,也只居其一 R 是一个全序集.( 3 ) R 中的元素满足阿基米德性:对 R 中的任意两个正数 a , b ,必存在自然数 n ,使得 na >b.2 .实数集合 R 是一个完备集定义1.1(距离空间)设 X 是一个集合,定义映射+→⨯R X X :ρ,满足 ( 1 )非负性:对();0,,,y x y x X y x =⇔=∈∀ρ ( 2 )对称性:()()x y y x ,,ρρ= ;( 3 )三角不等式:()()()y z z x y x ,,,ρρρ+≤;则称ρ是点集 X 上的一个距离.如果 X 是一个线性空间,称()ρ,X 是一个距离空间 。
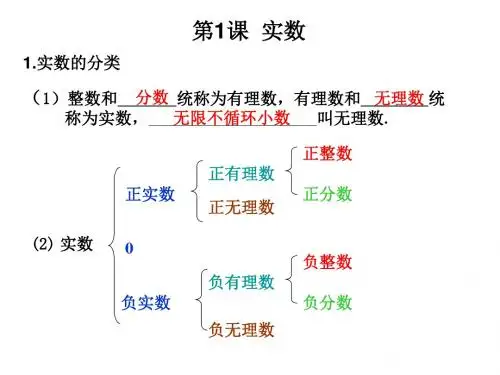
第一章 实数集与函数§1 实数一 实数及其性质 有理数可用分数形式p q(,p q 为整数,0q ≠)表示,也可以用有限十进小数或无限十进循环小数来表示;而无限十进不循环小数则称为无理数.有理数和无理数统称为实数。
规定:对于正有限小数(包括正整数)x ,当012.n x a a a a = 时,其中009,1,2,,0,i n a i n a a ≤≤=≠ 为非负整数,记012.(1)999n x a a a a =- ;而当0x a =为正整数时,则记0(1).999x a =- 。
对于负有限小数(包括负整数)y ,则先将y -表示为无限小数,再将所得无限小数之前加负号。
又规定数0表示为0.000 。
于是,任何实数都可用一个确定的无限小数来表示。
定义1 给定两个非负实数012012.,.n n x a a a a y b bb b == ,其中00,a b 为非负整数,,(1,2,)k k a b k = 为整数,09,09k k a b ≤≤≤≤。
若有(0,1,2,k k a b k == ,则称x 与y 相等,记为x y =;若00a b >或存在非负整数l ,使得(0,1,2,)k k a b k l == 而11l l a b ++>,则称x 大于y ,记为x y >或y x <。
对于负实数x 与y ,当x y -=-时,规定x y =;当x y ->-时,规定x y <(或y x >)。
规定任何非负数实数大于任何负实数。
定义2 设012.,n x a a a a = 为非负实数。
称有理数012().n n x a a a a = 为实数x 的n 位不足近似,而有理数1()()10n n n x x =+称为实数x 的n 位过剩近似,0,1,2,n = 。
对于负实数012.,n x a a a a =- 其n 位不足近似与n 位过剩近似分别规定为0121().10n n nx a a a a =-- 与012().n n x a a a a =- 。
第一讲实数与实函数1 . 1 实数与实函数的基本概念一.实数实数包括有理数和无理数.有理数,就是能够表示成qp形式的数,其中 p 是整数, q 是不为零的整数.如果用小数表示,有理数都可以表示成有限小数,或无限循环小数.无理数,就是不能表示成qp形式的数,也就是无限不循环的小数.如果将有限小数也表示成无限小数,例如:数 1 可表示为 1=1.000… ;也可以表示为 l=0.999… (注:这是实无限的观点),为唯一性起见,数学上作了一个约定,就是不以零为循环节.数 1 约定的表示为l=0.999…,因此,实数就是一个可以用无限小数表示的数.二、实数的性质1 .实数集合 R 是一个阿基米德有序域( 1 )在实数集合 R 上定义加法“ + ”和乘法“× ”两种运算,对两种运算分别满足交换律、结合律,以及乘法关于加法的分配律;对加法,有“零元”和“负元”;对乘法有“单位元”和“逆元” ; R 成为一个“域”.( 2 )在集合 R 上定义了一种序关系“ < " ,且满足传递性:即对 R c b a ∈∀,, ,若 a < b , b < c ,则 a <c ;三歧性:即对 ,,R b a ∈∀,关系 a < b , a =b , a > b 三者必居其一,也只居其一 R 是一个全序集.( 3 ) R 中的元素满足阿基米德性:对 R 中的任意两个正数 a , b ,必存在自然数 n ,使得 na >b.2 .实数集合 R 是一个完备集定义1.1(距离空间)设 X 是一个集合,定义映射+→⨯R X X :ρ,满足 ( 1 )非负性:对();0,,,y x y x X y x =⇔=∈∀ρ ( 2 )对称性:()()x y y x ,,ρρ= ;( 3 )三角不等式:()()()y z z x y x ,,,ρρρ+≤;则称ρ是点集 X 上的一个距离.如果 X 是一个线性空间,称()ρ,X 是一个距离空间 。
在实数集 R 上定义距离()y x y x -=,ρ(可以验证满足定义中的三条),则()ρ,R 是一个距离空间.定义 1 . 2 设{}n x 是距离空间()ρ,X 中的点列,若对0,0>∃>∀N ε,当 m , n > N 时,恒有()ερ<m n x x ,,则称{}n x 是 X 中的柯西列.定义 1 . 3 若距离空间 X 中的任意柯西列都在 X 中收敛,则称 X 是完备的距离空间. 由柯西收敛准则很容易知道,作为距离空间的实数集 R 是完备的.有 6 个刻划实数集 R 完备性的且彼此等价的定理,它们分别是( 1 )确界原理:设 S 是非空数集.若 5 有上界.则 S 必有上确界;若 S 有下界,则 S 必有下确界.( 2 )单调有界原理:单调有界点列(函数)必存在极限. ( 3 )区间套定理:若[]{}n n b a ,是一个区间套,则存在唯一的实数ξ,使得[],2,1,,=∈n b a n n ξ …,即 ,2,1,=≤≤n b a n n ξ…。
( 4 )有限覆盖定理:设 H 是对闭区间巨,习的一个任意开覆盖,则从 H 中可选出有限个开区间来覆盖[]b a ,( 5 )聚点定理:实轴上的任一有界无限点集 S 至少有一个聚点. 推论(致密性定理):有界点列必有收敛子列. ( 6 )柯西收敛准则:数列{}n a 收敛的充要条件是数列{}n a 是柯西列. 关于上述六个定理的等价性证明可参考文献[]1.三、关于实数点集的一些重要概念1 .有界点集S 是一实数点集,若0>∃M 使对S x ∈∀恒有M x ≤,则称 S 是有界点集. 2 .无界点集S 是一实数点集.若对0>∀M ,S x ∈∃使得M x ≥,则称 S 是无界点集. 3 .有界函数f ( x )是定义在点集 I 上的函数,若0>∃M 使对I x ∈∀ 恒有()M x f ≤,则称f ( x )在I 上有界. 4 .无界函数f ( x )是定义在点集 I 上的函数,若对0>∀M ,I x ∈∃使得()M x f ≥ .则称 f ( x )在 I 上无界、例 1 . 1 证明函数()x x f 1=在()1,0上无界 证明:对0>∀M ,()1,0110∈+=∃M x 使得()M M x f >+=1故()xx f 1=在( 0 , 1 )上无界。
5 .上确界设 E 为一个实数点集, a 为一是实常数,若满足: ① 对E x ∈∀ ,恒有α≤x (即α为E 的上界); ② 对0>∀ε,存在E x ∈0 ,使得εα->0x 。
(即α是 E 的最小的上界),则称α为 E 的上确界,记作E sup =α 6 .下确界设 E 为一个实数点集,β为一是实常数,若满足: ① 对E x ∈∀,恒有β≤x (即β为E 的下界); ② 对0>∀ε,存在两E x ∈0,使得εβ+>0x (即β是 E 的最大的下界),则称β为 E 的下确界,记作E inf =β.注:点集 E 的上确界或下确界可以属于 E ,也可以不属于E 命题( 1 ) E sup =α,则E E max =⇔∈αα.( 2 )E inf =β,则E E min =⇔∈ββ. 证明显然,请读者自证.例 1 . 2 设A 、B 皆为非空有界集,定义数集{}B y A x y x z z B A ∈∈+==+,,|证明: ( 1 ) sup ( A + B ) = supA + SupB ;( 2 ) inf ( A + B )= InfA + infB .证明: ( 1 )由已知, A 、 B 非空有界,可知 A +B 也是非空有界集.根据确界原理,它们的上、下确界都存在.对B A z +∈∀ ,由定义,存在A x ∈ 及B y ∈使得B A y x z sup sup +≤+=即实数 supA 十 supB 是数集 A +B 的上界;又对B A z +∈∀,B y A x ∈∈∃'',,使得,2sup 'ε->A x ,εε-+>+⇒->B A y x B y sup sup 2sup '''记B A y x z +∈+='''则ε-+>B A z sup sup ':.由定义可得sup ( A + B )= SupA + supB( 2 )证明与( 1 )类似,从略. 例 1 . 3 设 f 在区间 I 上有界.记(),sup x f M Ix ∈=(),inf x f m Ix ∈=证明:()()m M x f x f Ix -=-∈'''sup证明:对I x x ∈∀''',,有(),'M x f m ≤≤(),''M x f m ≤≤则()()m M x f x f -≤-''' ()*又对0>∀ε,I x x ∈∃21,使得()()2,221εε+<->m x f M x f ()**可得()()()ε-->-m M x f x f 21由式()*,式()**可知()()m M x f x f Ix x -≤-∈''''''sup7.聚点定义 1 . 4 (点集的聚点):设 E 是一个点集,ξ是一个点,若在ξ的任意邻域内都含有 E 的无穷多个点,则称ξ为点集 E 的聚点.命题 设 E 是一个点集,ξ是一个点,下列说法等价: ( 1 )ξ为点集 E 的聚点.( 2 )在ξ的任意邻域内都含有 E 的异于ξ的一个点. ( 3 )在 E 中存在互异的点列{}n x 使得ξ=∞→n n x lim证明: (1)⇒(2 ) .显然.(2)⇒ (3) .取11=ε ,在()1;εξ⋃)内,{}ξ\1E x ∈∃,取0,21min 12>⎭⎬⎫⎩⎨⎧-=ξεx ,在()1;εξ⋃内,{},...,\2ξE x ∈∃一般地,取0,1min 1>⎭⎬⎫⎩⎨⎧-=-ξεn n x n 在()n εξ;⋃内,,{},...,2,1,\=∈∃n E x n ξ 显然{}E x n ⊆ E ,且是互异的,同时显然有ξ=∞→n n x lim( 3 ) ⇒ ( 1 ) .对0>∀ε ,0>∃N ,当 n > N 时,{}()εξ,U x n ⊂.注意到,...,2,1,=∈n E x n ,即ξ为点集 E 的聚点.注: ( 1 )从定义可知,有限点集必无聚点.( 2 )点集 E 的聚点可以属于 E ,也可以不属于 E .例如,设 A 是开区间( 0 ,1 )中的所有有理点所构成的集合,则闭区间[]1,0中的所有点都是 A 的聚点定义 1 . 5 (点列的聚点):设{}n x 是一个点列,ξ是一个点,若在ξ的任意邻域内都含有{}n x 的无穷多项,则称ξ为点列{}n x 的聚点.注意:点集的聚点与点列的聚点不同,例如{}n x =(){}n1-作为点列,它有两个聚点:-1 和1 ,但是如果把它们看做点集,则它是一个仅含有两个元素的集合{}1,1-,无聚点.把点列的最大(小)聚点,叫做点列的上(下)极限,分别记作n n x -∞→lim 和n n x lim∞→- .8.覆盖设{}Γ∈∆=a H a |是一个开区间集,其中Γ是一个指标集,a ∆是开区间.设 I 是一个点集,如果对I x ∈∀ ,总存在H a ∈∆ ,使得a x ∆∈,称 H 覆盖了I ,或称 H 是 I 的一个开覆盖.如果 H 是有限集而覆盖了 I ,则称 H 是 I 的一个有限开覆盖;如果 H是一个无限集合而覆盖了 I ,则称 H 是 I 的一个无限开覆盖.前面提到的有限覆盖定理,是一个十分重要的定理.它可以推广到一般的距离空间上去,这里就不多说了.例 1 . 4 {}n x 是单调数列,证明:若{}n x 存在聚点,则必是唯一的,且是{}n x 的确界. 证明:不妨设{}n x 是单调递增数列.假设 A , B 都是它的一个聚点,且不等.不妨设B A >,由聚点的定义,取02>-=BA ε,在()ε;A U ,含有{}n x 的无穷多项,假设{}()ε,0A x x n n ⋃⋂∈,则20BA A A x n -=-<-ε,又根据{}n x 是单调递增的,当0n n >时2BA x n +>,,即在 U ()ε;B 内至多含有{}n x 的有限项,与 B 是聚点矛盾.再证{}n x A sup =:首先证明对A x n n ≤∀,事实上,假设有某一项0n x > A ,插人0ε,使A x n >>00ε.由{}n x 的单增性,当0n n >时,A x x n n >>>000ε .此与 A 为聚点矛盾.与唯一性的证明类似,可以证明 A 必是最小的上界,即{}n x A sup = .注:此题可有一个推论:若{}n x 是单调数列,且有聚点,则必收敛.若{}n x 是单调增,则n n n x x sup lim =∞→;若{}n x 是单调减的,则n n n x x inf lim =∞→.四、实函数( 1 )要理解函数的定义,一定要搞清楚映射的定义,而一元实函数实际上就是一个从实数集到实数集的映射,这里不去赘述.确定一个函数的基本要素是定义域和对应法则,当然函数的值域也是函数的要素之一,但它是随定义域与对应法则而定的.( 2 )函数的运算包括: ① 四则运算; ② 复合运算; ③ 极限运算; ④ 微分运算; ⑤ 积分运算; ⑥ 取大(小)运算()(){}()(){}()x g x f x g x f ,m in ,,m ax 等.这里需要特别强调的是,要注意它们的定义域,使得上述运算有意义.( 3 )几种具有特性的函数: ① 有界函数(上节已给出定义); ② 单调函数; ③ 奇、偶函数; ④ 周期函数.这些函数的基本概念不再赘述.( 4 )初等函数与非初等函数.①六类基本初等函数:常函数、幂函数、指数函数、对数函数、三角函数、反三角函数.② 初等函数:由基本初等函数经过有限次四则运算与复合运算所得到的函数,统称为初等函数.③ 非初等函数:不是初等函数的函数,称为非初等函数.一般的分段函数,都是非初等函数,例如符号函数⎪⎩⎪⎨⎧<-=>=0,10,00,1sgn x x x x 就是非初等函数,但是分段函数⎪⎩⎪⎨⎧<-=>=0,10,00,1x x x x 可以看做初等函数,因为2x x =是两个幂函数的复合下面几个非初等函数都很重要: 狄利克雷( Dirichlet )函数()⎩⎨⎧=为无理数,为有理数x x x D 0,1。