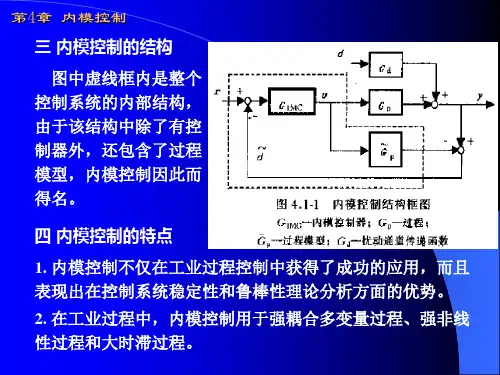
第4章内模控制

格式：ppt
大小：1001.50 KB
文档页数：30

下载文档原格式

4讲内模控制IMC与Smith预估器

越大响应越慢，操作变量变化柔和。
若
r 1，如对 r 2 ，滤波器：
1 f ( s) 2 2 s 2s 1
（10）
取
0.5
可使ISE最小
（2）若输入为斜坡响应无差，则 f 必有附加条件
利用式（8）
d ~ 由 [G p ( s)G IMC ( s)] s 0 0 得 ds
f ( s ) 为低通滤波器，有理化调整；目的是使 GIMC 变为有理；
则闭环 y ( s) 及 e( s) ：
~ [ G ( s ) G ( s )] ~ ~ P P 式中 e H (s) GP f (s) 为灵敏函数， ~ m GP ( s)
~ G P f ( s)[1 em ] y( s) [r ( s) Gd d ( s)] Gd d ( s) ~ 1 G P f ( s )e m ~ H ( s)[1 em ] [r ( s) Gd d ( s)] Gd d ( s) （5） ~ 1 H ( s )e m ~ 1 GP f ( s) e( s ) r ( s ) y ( s ) [r ( s) Gd ( s) d ( s)] ~ 1 G P f ( s )e m ~ 1 H ( s) [r ( s) Gd ( s) d ( s)] ~ （6） 1 H ( s )e m
~ 1 Ts 1 s 0 不可实现的预测 e ；过程模型的逆： G p K
Ts 1 ~ 1 选IMC控制器： G IMC ( s) G p f K (s 1)
取 T ，则 GIMC 为超前环节当模型匹配时，闭环响应： e s e s y( s) r ( s) [1 ]d ( s) s 1 s 1

内模控制

然后在反馈和输人通道上增加反馈滤波器
和输人滤波器
，通过调整滤波器的结构和参数，使系统获得所期望的性能。下面就对开环稳定过程进行离散内模控制器设计。
考虑一般情况，令被控对象为有纯滞后的非最小相位过程，则过
程模型可分解为两部分：
控制器取为：设计时为保持闭环系统零稳态偏差特性，需满足：
可实现因子可取为:
经输人滤波器
后再送至控制器。
经柔化后的输人参考轨迹的一般形式为:
即
第4章内模控制 4.6 简化模型预测控制（SMPC）内模控制是一种极具理论价值的基于模型的控制策略，但其工程实
现因涉及模型求逆和滤波器合理设计等问题，设计过程较为复杂，尤
其是对于多输人多输出过程，实施难度更大。 1987年以后，Arulalan等人提出了一种简化模型预测控制(SMPC)，其
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
第4章内模控制
对于模型无差，即 em (s) 的 0特殊情况，上式可简化为：
以上两式表明：对于无模型失配的情形，闭环传递函数
除了
中必须包含所有的滞后和右半
平面零点，且必须有足够的阶次来避免物理上的不可实
现外，其他都是可以任意选择的。因此，闭环响应可以直接设
第4章内模控制 4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
情形B.具有右半平面(RHP)零点
第4章内模控制
4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时，内模控制系统的性质仍
然成立。在离散时间条件下，设计内模控制器也仍然分为两步进行：首先是设计一个稳定的理想控制器；

内模控制和Smith预估器

第五节 Smith 预估控制Smith 预估控制方法是在1957年由Smith 提出来的，其特点是预先估计被控系统在基本扰动下的动态特性，然后用预估器进行补偿，力图使被延迟的被控制量超前反映到控制器中，使控制器提前动作，从而显著地减小系统的超调量，同时加速系统的调节过程。

一、Smith 预估控制原理预估控制系统原理图如图7-24所示。

(a) 预估控制系统原理框图 (b) Smith 预估器图7-24 预估控制系统原理图图中，s e s G τ−)(p 为具有时滞为τ的对象传递函数，其中)(p s G 为被控对象；)(m s G 为内部模型（又称为对象的标称或名义模型），即Smith 预估器的传递函数，()s e s G s G τ−−=1)()(p m ；)(s D 为（前馈）内模控制器；)(s d 为扰动；)(s R 为参考输入；)(s Y 为被控对象输出；)(m s Y 为内部模型输出。

由图7-24可知，将Smith 预估器与控制器（或被控对象）二者并联。

在理论上可以使被控对象的时间滞后得到完全补偿，控制器的设计就不必再考虑对象的时滞作用了。

现在，系统中假设没有补偿器（预估器），则控制器输出与被控量之间的传递函数便为 s e s G s U s Y τ−=)()()(p (7-50) 上式表明，受到)(s U 控制作用的被控量)(s Y 要经过纯滞后时间τ之后才能反馈到系统控制器输入端。

若采用预估补偿器，则控制量)(s U 与反馈到控制器输入端的反馈信号)(s Y ′之间的传递函数乃是两个并联通道之和，即)()()()(m p s G e s G s U s Y s +=′−τ (7-51) 为使反馈信号)(s Y ′不发生时间滞后τ，则要求(7-51)式满足)()())(()()(p m p s G s G e s s G s U s Y s =+=′−τ (7-52) 于是，就导出了Smith 预估补偿器的传递函数为()s e s G s G τ−−=1)()(p m (7-53) 在系统中设置了Smith 预估器的情况下，可以推导出系统的闭环传递函数为)()(1)()()1)(()(1)()(1)1)(()(1)()()()(p p p p p p s G s D e s G s D e s G s D e s G s D e s G s D e s G s D s R s Y s s s s+=−++−+=−−−−−ττττ (7-54) 由上式可以明显看出，在系统的特征方程中，已经不含有s e τ−项。

内模控制

第二章基本概念............................................................................................................. 4
2.1、鲁棒性与鲁棒控制 .......................................................................................... 4
3.2、前馈控制器 Q 的设计 ....................................................................................... 9
3.3、反馈滤波器 F................................................................................................... 10
1.2、发展现状
经过十多年的发展，IMC 方法不仅已扩展到了多变量和非线性系统，还产生了多种设计方法，较典型的有零极点对消法、预测控制法、针对 PID 控制器设计的 IMC 法、有限拍法等。IMC 与其他控制方法的结合也是很容易的，如自适应 IMC，采用模糊决策、仿人控制、神经网络的智能型 IMC 等.值得注意的是，目前已经证明，已成功应用于大量工业过程的各类预测控制算法本质上都属于 IMC 类，在其等效的 IMC 结构中特殊之处只是其给定输入采用了未来的超前值(预检控制系统)，这不仅可以从结构上说明预测控制为何具有良好的性能，而且为其进一步的深入分析和改进提供了有力的工具。
内模控制器设计：摘要将内模控制器和传统的 Smith 控制器进行比较对照，总体论述内模控

内模控制在多电机同步驱动系统中的应用

刘立伟刘福才张学莲
摘
要
根据协调控制原则，采用内模控制原理，并结合
统的同步关系等等。一般说来，调关系是各受控协
量应满足的某种线性或非线性函数关系
工程设计方法，针对直流电动机同步驱动问题，通过理论
分析和仿真研究，找出了一种较好的同步方案。这种方案
系；化工，热工生产过程中各反应物质或原料成分
的比例关系；电力系统中各电站或机组的负荷分配关系；垂直升船机，大型龙门吊车的多电机驱动系
２００２年２月２６日收到
出的。它设计简单，跟踪调节性能好，鲁棒性强，能消除不可测干扰的影响。
种在速度调节器上引入转速微分负反馈的方法，它可以抑制甚至消除转速超调，降低负载扰动引起的动态速降，过强的微分负反馈会使系统的响应变但缓。文献［，５出了采用Ｉ４】提－Ｐ控制器取代Ｐ调Ｉ节器的方法，它可以减小转速超调，但文献［】６指出，采用Ｉ控制器会限制系统的最大工作速度，・Ｐ只能在一定的调速范围内具有良好的起动特性。为解决这一问题，本文对各电机采用内模控制方法进行调速。内模控制方法是Ｇｒｉ９２年提ａｃａ１８
ａｄｃｍｂｎｎｔｎｉｅｒｎｅｉｎｍｅｈｄａｇｏｃｅｎｏｉｉｇｗｉｅｇｎｅｇｄｓｇｔｏ，ｏｄｓｈ－ｈｉ

过程控制工程智慧树知到答案章节测试2023年中国石油大学(华东)

第一章测试1.广义对象包括（）。

A:被控对象B:检测元件C:执行器D:控制器答案:ABC2.先进控制有（）。

A:时滞补偿B:故障诊断C:预测控制D:解耦控制答案:ABCD3.过程控制系统中，代替人眼睛的是（）。

A:执行器B:控制器C:检测装置D:被控对象答案:C4.控制系统组成中具有大脑功能的是（）。

A:控制装置B:检测装置C:执行机构D:被控对象答案:A5.控制目标中不需要考虑环保因素。

A:对B:错答案:B6.随动控制系统的设定值是随时间变化的。

A:对B:错答案:A第二章测试1.被控对象的动态特性是描述被控对象输入输出关系动态特征的。

A:错B:对答案:B2.稳态指的是被控量不再随时间变化时，系统处于平衡状态。

A:对B:错答案:A3.误差绝对值积分（IAE）准则可避免正负积分面积相消现象。

A:对B:错答案:A4.灰箱模型是基于过程动态学的机理建模。

A:对B:错答案:B5.调节通道对象特性的T0小对控制系统有利。

A:错B:对答案:B6.比例积分作用为系统增加了一个开环零点，使系统相角超前，增加了稳定性。

A:错B:对答案:B7.调节系统在纯比作用下已整定好，加入积分作用后，为保证原稳定度，此时应将比例度（）A:减小B:不变C:增大D:先增大后减小答案:C8.对于气动执行机构，当信号压力增加，推杆下移的，称该气动执行机构为A:可调式B:反作用式C:正作用式D:移动式答案:C9.在控制系统中，工艺变量需要控制的生产过程、设备或机械等，称为（）A:反馈B:控制器C:被控过程D:设定值答案:C10.下面对过程的控制质量没有影响的是（）A:扰动通道放大倍数B:扰动通道时间常数C:控制通道放大倍数D:扰动通道纯滞后时间答案:D11.过渡过程品质指标中，余差表示（）A:新稳态值与给定值之差B:测量值与给定值之差C:超调量与给定值之差D:调节参数与被调参数之差答案:A12.下列哪个参数不是描述对象特性的参数（）A:tB:TC:KD:τ答案:A13.受控制器的操纵，使被控变量保持在设定值的物理量是（）A:操纵变量B:被控对象C:设定值D:测量值答案:A14.在阶跃扰动作用下，过程控制系统的过渡过程出现的形式如下，（）是一种稳定控制系统A:非振荡发散过程B:衰减振荡过程C:发散振荡过程D:等幅振荡过程答案:B15.以下哪个传递函数可以表示积分环节（）A:TsB:KC:K/(Ts)D:K/(Ts+1)答案:C16.PID参数整定方法有（）A:响应曲线法B:临界比例度法C:继电器型PID自整定法D:经验法答案:ABCD第三章测试1.下列哪种不属于复杂控制系统？A:流量控制系统B:前馈控制系统C:串级控制系统D:解耦控制系统答案:A2.串级控制对所有的干扰都有很强的克服能力A:对B:错答案:B3.串级控制副参数的选择需要注意的问题有（）？A:副参数必须可测B:调节阀与副参数之间具有因果关系C:尽可能将带有非线性或时变特性的环节包含于副回路中D:副参数的选择应使副对象的时间常数比主对象的时间常数小答案:ABCD4.串级控制多用于（）场合？A:用于所有的控制场合；B:用于时滞较大的对象；C:用于对象具有较大的非线性特性，且负荷变化较大；D:用于克服变化剧烈和幅值大的干扰；答案:BCD5.均匀控制有（）两种形式？A:前馈均匀控制B:单回路均匀控制C:串级均匀控制D:比值均匀控制答案:BC6.前馈控制的基本原理是（）？A:可变性原理B:等价原理C:不变性原理D:抗干扰原理答案:C7.动态前馈的效果一定比静态前馈的效果好。

神经网络内模控制 PPT课件

7
内部模型辨识目标函数
8
内模控制过程及结果2
（2）系统输入：
r (k ) 是周期 k 100 的方波
9
控制系统输入、输出：r、y
112
内部模型辨识目标函数
13
结束
14
例3 神经非线性内模控制
1
一阶 SISO 可逆、具有一阶时延的非线性系统，仿真模型：
y (k 1) 0.8 sin( y (k )) 1.2u (k )
（1）系统输入：
r (k ) 1(k )
输出端干扰： ( k 50) 0.1( k ) （2）系统统输入：
r (k ) 是周期 k 100 的方波
P( z )
y ˆ y
内部模型 e1
ˆ ( z) P
0.5
内模控制结构
3
内模控制过程及结果1
（1）系统输入：输出端干扰：
r (k ) 1(k )
(k 50) 0.1(k )
4
控制系统输入、输出、扰动：r、y、v
5
内模控制器输出：u
6
内模控制器、内部模型调整
2
内模控制设计
• 神经模型辨识器结构 1 BP网络N1,3,1 +两个 z • 内模控制器设计取具有一阶时延对象逆模型结构与例2逆模型辨识器同 • 滤波器设计取滤波器：
F ( z) 1 , 0 1 1 z 1
r e
_
滤波器
F ( z)
g
内模控制器
D( z )

u
对象

第4章_内模控制

4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
情形B.具有右半平面(RHP)零点
第4章内模控制 4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时，内模控制系统的性质仍然成立。在离散时间条件下，设计内模控制器也仍然分为两步进行：首先是设计一个稳定的理想控制器；然后在反馈和输人通道上增加反馈滤波器和输人滤波器，通过调整滤波器的结构和参数，使系统获得所期望的性能。下面就对开环稳定过程进行离散内模控制器设计。考虑一般情况，令被控对象为有纯滞后的非最小相位过程，则过程模型可分解为两部分：
热交换器出口温度与蒸汽流量的关系可由开环阶跃响应的实验获得:
第4章内模控制 (二) 内模控制器设计
(i)对象模型分解: (ii)滤波器设计（即IMC控制器设计）:
(三) 算法实现
控制器传递函数为:
模型匹配时
思考:SMPC的缺陷？
第4章内模控制 4.7 内模控制的工业应用
4.7.2 热交换器温度控制
右图所示是一个蒸汽加热器实验装置，加热介质为蒸汽，冷流体为水。控制目标是通过调节加热蒸汽流量来保证热交换器出口热水温度平稳。图中温度控制器采用微机实现。
(一) 对象建模
第4章内模控制 4.3 内模控制器设计——连续过程基本内模控制结构
• IMC→常规控制器：
GIMC (s) Gc (s) 1 GIMC (s)Gm (s)
第4章内模控制常规的反馈控制系统
• 常规控制器→IMC：
Gc (s) GIMC (s) 1 Gc (s)Gm (s)
第4章内模控制一、内模控制器设计应分两步进行：

内模控制在过程控制系统中的应用研究

型。本文针对ＰｃＴ．Ⅲ型过程控制实验装置，选取上水箱液位作为被控对象＋通过开环阶跃响应进行系统
ｃ，（Ｂ）＝黼“ 辨识”］，得到上水箱液位对象的数学模型为：＾ｆ（ｇ）
∞，２靠图２瑚ｃ结构等效变换为经典控制结构
等，＝揣类似地，图２中的输人输出关系可以表达为：㈣
器２丽丢丽
（３）
所阻，系统的闭环响应为：
２００７年第１２期文章编号：１００６—２４７５（２００７）１２．００４９—０３
计算机与现代化Ｊ王ｓＵＡＮＪＩＹＵＸＩＡＮｎＡＩＨＵＡ
总第１４８期
内模控制在过程控制系统中的应用研究
杨大勇
南昌大学环境科学与工程学院，江西南昌３３００３１）
摘要：内模控制是一种简单、宾用的先进控制算法，是研究其它基于模型的控制蕈略的理论基础。本文介绍了内棰控制
３结束语
本文介绍了内模控制器的基本原理和设计方法，
参考文献：
Ｃｌ】ＧＴ帅ｈ“ｉ＾ｃⅢＥⅫ，Ｍ％∞ｄｌｒｈｉ［ＭＪ．】ｈ咖．ｄｍｈｏｌ捌ｄ．ａ呷Ｅ耐％．ｃｍｈ吲ｅｎｎｇ№廿
Ｄ曙．１粥２．２１（２）；３∞０∞．［２】王树青．等．先进控制技术及其应用［Ｍ】．北京：科学出
腹社，２００１．
［３］高东杰，谭杰林，红权．应用先进控制技术［Ｍ］，北京：国防工业出版社．２００３．赵曜．内模控制发展综述［Ｊ】．信息与控制，２０００，凹（６）：５２６｛３１．
用模拟硬件或计算机软件来实现，该结构中除了有控制器Ｇ眦以外，还包含了过程模型ｃＰ。为了求取图ｌ中输人ｒ和ｄ与过程输出ｙ之间的传递函数，可以将图１等价变换为图２所示的简单反馈控制系统形式，即ＩＭｃ的等价结构。
这样对于图２中的内环反馈控制器有
收稿日期：２００６．１１４０作者简介：杨大勇（１９７８．）．男．安徽怀远人。南昌大学环境科学与工程学院讲师，博士研究生，研究方向：先进过程控制技术与应用。

内模控制和Smith预估器

一、Smith 预估控制原理预估控制系统原理图如图7-24所示。

由图7-24可知，将Smith 预估器与控制器（或被控对象）二者并联。

在理论上可以使被控对象的时间滞后得到完全补偿，控制器的设计就不必再考虑对象的时滞作用了。

内模与预测控制

D(s) = 0, R(s) ≠ 0
这表明本控制器是输出跟踪 R 变化的理想控制器。
小结
内模控制是在“模型没有误差且模型可倒”假设条件下的理想反馈控制器
完全跟踪设定的变化完全抑制扰动的影响
实际应用中假设条件可能不成立，尤其是对模型准确性的要求，内模控制结构仍然可以实施，但需要做调整预测控制可以认为是内模控制的2006-06-13
提纲
内模控制预测控制
内模控制
系统结构图
ˆ G p (s )
系统传递函数
理想控制器
情形I：系统工作在平衡态，有外界扰动
R(s) = 0, D(s) ≠ 0
这表明本控制器是克服外界扰动的理想控制器。
理想控制器
情形II：系统工作点切换，无外界扰动
预测控制
浙大预测控制ppt
先进控制
先进控制中“先进”具有时代的特征当前的先进控制由一系列控制方法组成
以预测控制为核心共同特征：具有较复杂的算法结构，由计算机的软件实现
参考文献
《工业过程控制工程》，王树青等编著，化学工业出版社，2003年1月。《工业过程先进控制》，俞金寿主编，中国石油出版社，2002年2月。王慧，预测控制ppt “第五讲——MPC”，浙江大学。

内模控制与预测控制

若无模型误差时仿真结果如下：
若实际对象模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e −0.9 s
，兼顾输出的平稳性和调节时间，反馈
滤波取α = 0.7 比较合适，仿真结果如下：
1.2 有限拍法设计控制器 Q 标称模型 Pm 的极点为 λ1 = 1.5262 + 0.6235i 和 λ2 = 1.5262 − 0.6235i
内模控制与预测控制
姓名：张慧勇学号：S082121
1 内模控制
已知对象的标称模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e−s
若采样周期Ts = 0.2 ，相应的离散模型为
Pm (z)
=
1.468z − 0.9789 z2 −1.123z + 0.3679
z −5
对象的纯时滞为 5，取 λ = z−1 ，则离散模型为
2.3.3 控制量权重 ρ = 3 时，仿真结果如下：
由上面 3 个仿真结果可知增大控制量权重 ρ ，对象输入（控制器输出）减小，系统的快速性减慢，平稳性增加。
2.4 Matlab 程序代码
以下代码为 Simulink 控制器 GPC 的程序代码
function [sys,x0,str,ts]=GPC(t,x,y,flag)
若无模型误差时仿真结果如下：
若实际对象模型为
Pm (s)
=
10s + s2 + 5s
20 + 10
e −0.9 s
，，兼顾输出的平稳性和调节时间，反
馈滤波取α = 0.8 比较合适，仿真结果如下：

一种基于干扰观测器的内模控制方法

制领域，带干扰观测器的控制策略因其干扰抑制能力强和计算量小等特点被广泛应用Ｊ。文献［７］通
过终值定理证明了干扰观测器能够在有限时间内
收稿日期：２０１３－０１－０４
作者简介：王文波（１９８７一），男，硕士研究生，主要研究方向为先进控制技术及其应用。
有结构上的优势。周期扰动是控制系统中常见的一类扰动，通常产生于质量不平衡振动或执行机构带来的高频振动ｊ：如硬盘驱动控制。考虑内模控制器的实现问题和闭环系统的鲁棒稳定性要求，需要在设计过程中引入滤波器，常见的滤波器有Ｉ型和 Ⅱ型＿３Ｊ。含滤波器的内模控制器能够抑制阶跃干扰，但当被控对象中有小极点时，干扰抑制速率会受此极点影响。文献［３］针对
踪滞后和无法有效抑制正弦扰动。针对这一问题本文提出了一种基于干扰观测器（ＤＯ）的内模控制方
法。该方法能够抑制由阶跃扰动和正弦扰动组成的复合扰动：通过观测器可以对正弦干扰进行观测和补偿，内模控制器抑制阶跃干扰和观测器的补偿误差。对单机械臂的仿真证明了该方法的有效性。
第３４卷
第４期
太
原
科
技
大
学
学
报
Ｖｏ１．３４Ｎｏ．４
Ａｕｇ．２０１３

1.内模概论

P1
e-τs
Smith预估控制的等效结构
控制器Q
u
对象P 模型Pm
y
ym em
内模控制的基本结构
注：IMC与传统反馈控制在表达式上也可等价转换
Q C C 或 Q 1 QPm 1 CPm
Q
P Pm
C
P
但 Pm 有时滞时的控制器结构并不相同： IMC的C中有时滞环节，而其标称（nominal）闭环传函QPm 的分母中不含时滞；而传统反馈的C虽不含时滞（有理分式），但其标称的闭环传函分母1+CPm 中包含时滞（易引起不稳定或性能恶化）。
内
1. 2. 3. 4. 5. 6. 7.
容
内模控制的产生背景时滞系统的开环与闭环控制内模控制基本结构与特点 Smith预估控制与内模控制内模控制结构的改进内模控制与智能控制的结合内模控制的研究动态
1. 概述
1.1 IMC的产生
美国的 Garcia 与 Morari 1982年正式提出 IMC Industrial & Engineering Chemistry ( I&EC Process Des. Dev., V.21, p308) 提出的背景有两个
4. 舒迪前，预测控制系统及其应用，机械工业出版社，1996年
5. 席裕庚，预测控制，国防工业出版社，1993年
第一部分内模控制
( IMC, Internal Model Control )
内模控制（ IMC ）简介
Internal Model Control
之所以叫“内模控制”是因为其控制结构中包含受控对象的模型；是先进控制的代表性方法之一，且与预测控制本质上属于同一类；是一种实用性很强的控制方法，其结构简单、设计直观简便、在线调节参数少、且调整方针明确、调整容易，鲁棒性强，对大时滞系统也能很好地控制；早期主要用于工业过程控制，现在已扩展到很多领域，包括电机调速、机器人等。

IMC控制

p
p 1
如果过程包含N个采样周期的纯滞后，则 ˆ ( z ) z ( N 1) G
p
反映采样过程的固有延迟。
ˆ ( z ) z 1 。在过程没有纯滞后的情况下，G p
如果过程模型中包含有单位圆外的零点
z Vi 1 Vi ˆ Gp1 ( z ) z V 1 V i i ˆ ( z ) 的零点，而且式中， V 是 G

(a)IMC系统结构
D( s)
1 101 2s

1 10 s 1
e
10 s
Y (s)
比较IMC和Smith预估控制两种控制策略。
1 e 8 s
1 10 s 1
（b）Smith预估控制系统结构图6－4 存在模型误差时的系统结构图
(b)
(a) (a)不存在模型误差仿真输出
GIMC ( s) Gc ( s ) ˆ ( s) 1 GIMC （s)G p
可以看到控制器 Gc ( s) 的
因为在 s 0 时，
f ( s) 1 ˆ ( s) G ˆ ( s) G p p
得： Gc ( s) | s 0
零频增益为无穷大。因此可以消除由外界阶跃扰动引起的余差。这表明尽管内模控制器 GIMC ( s) 本身没有积分功能，但由内模控制的结构保证了整个内模控制可以消除余差。
f 是可调整参数，当 f 很小，能改善闭环性能，但对模型误差变得敏感；而当 f 较大时，则相反。
2 模型预测控制技术
模型预测控制算法是以模型为基础，同时包含有预测的原理；另外，作为一种优化控制算法，它还具有最优控制的基本特征。模型预测控制不管其算法形式如何，都具有以下三个基本特征；即模型预测、滚动优化和反馈校正。

内模控制器设计

问题：
(1) 当对象含有时滞特性时，控制器物理上是不可实现的； (2)当对象模型严格有理，而控制器非有理； (3) 当对象模型含有右半平面零点，致控制器本身不稳定，从而使闭环系统也不稳定； (4) 由理想控制器构成的控制系统，对于模型误差极为敏感，当模型不匹配时，无法确保闭环稳定性。
第二部分内模控制器设计
1
1.内模控制原理
内模控制系统结构如图所示
2
内模控制的核心有三部分：内部模型，用以预测被控对象的输
出并加以较正；内模控制器，调节控制量使生产过
程的输出跟踪控制系统的给定值；滤波器，改善控制系统的鲁棒性。
3
内模控制器的设计思路：使其传递函数为被控对象传递函数
的逆
即： Gc (s) Gm1(s)
8
4.内模控制器的设计步骤
第一步设计一个稳定的理想控制器，而不考虑系统的鲁棒性和约束；
第二步引入一个滤波器，通过调整滤波器的结构，使控制其物理可实现，通过参数调整来获得期望的动态品质和鲁棒性。
9
步骤1. 过程模型的分解：
Gm (s) Gm (s) *Gm (s)
步骤2 . IMC控制器设计
必须增加的值以克服它们的影响，而
的增加又提高了系统的鲁棒性。
19
u1 Gc * r
u2
Gc * Gm * u1 1 Gc * Gm
y p Gmu1 Gu1 Gpu2
16
对象稳定，要系统稳定，则要虚线框环节稳定。根据小增益理论
|| Gc (s)Gm (s) || 1
|| Gc (s)Gm (s)W * (s) || 117Fra bibliotek结论：
(1) IMC系统的本质是一种开环控制系统；

浙江大学博士入学考试线性系统控制理论真题03-09

9. (12 分) 已知线性定常系统
⎡ ⎢ ⎣
x&1 x&2
⎤ ⎥ ⎦
=
⎡ ⎢ ⎣
A11 A21
A12 A22
⎤ ⎥ ⎦
⎡ x1
⎢ ⎣
x2
⎤ ⎥ ⎦
+
⎡ B1
⎢ ⎣
B2
⎤ ⎥u ⎦
=
Ax
+
Bu
，
y
=
⎡⎣ I q
0⎤⎦ x = Cx
其中 x1 ∈ Rq ， x2 ∈ Rn−q ，试证明 {A,C} 完全能观测当且仅当 {A22 , A12 } 完全能观，设 {A,C}
−2⎥⎦
x
，
y
=
⎡a ⎢⎣1
2 4
b⎤ 1⎥⎦ x
试确定使系统完全能观时待定参数的取值范围。 4. (10 分) 给定连续时间的定常系统
⎧⎪ ⎨
x&1
⎪⎩
=
−x1x22 − (1+ x&2 = x12 x2
x1 )2
x1
判断其原点平衡状态是否为大范围渐进稳定。 5. (10 范围内) 已知某系统矩阵 A 满足
4
⎡-1 0 0 ⎤ ⎡1 0 ⎤
4.
x&
=
⎢ ⎢
0
⎢⎣ 1
-2 0
-3⎥⎥ x + ⎢⎢0 1 ⎥⎦ ⎢⎣0
1
⎥ ⎥
-1⎥⎦
u
，
y
=
⎡1
⎢ ⎣
0
2 1
0⎤ 1⎥⎦
x
，输出变换和状态反馈使闭环动态解耦，极
点 -1 ， -1+j ， -1-j ，求控制律。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

控制器传递函数为:
模型匹配时
思考:SMPC的缺陷？
第4章内模控制 4.7 内模控制的工业应用
4.7.2 热交换器温度控制
右图所示是一个蒸汽加热器实验装置，加热介质为蒸汽，冷流体为水。控制目标是通过调节加热蒸汽流量来保证热交换器出口热水温度平稳。图中温度控制器采用微机实现。
(一) 对象建模
热交换器出口温度与蒸汽流量的关系可由开环阶跃响应的实验获得:
第4章内模控制 (二) 内模控制器设计
(i)对象模型分解: (ii)滤波器设计（即IMC控制器设计）:
(三) 算法实现
第4章内模控制
4.3.2 滤波器设计
f (s) p(s) q(s) 取如下形式：
满足上式的滤波器最简单形式为：
滤波器可以采取其他形式，甚至可获得更快的响应。例如r＝2，滤波器可取为：
第4章内模控制
4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
结构和参数，可以有效地抑制输出振荡，且可获得所期望的动态特性和鲁棒性。
通常，反馈滤波器可选较为简单的一阶形式:
第4章内模控制
在反馈通道中插人滤波器，可使原来不稳定的闭环系统镇定下来，同时还有另外一个作用：就是可抑制干扰的作用。模型匹配时，由于干扰引起的输出为: 举例:
若已知输出端的干扰为指数上升形式，即
2. 类型2系统若闭环系统稳定，即使模型与过程失配，即 , 只要控制器满足，且则此系统属于类型2。该系统对于所有斜坡输入和干扰均不存在稳态误差。
第4章内模控制 4.2.3 内模控制的实现问题对于IMC系统，在模型准确情况下，只要令即可获得理想的设定值跟踪和完全的干扰抑制效果。然而，理想控制器性质常难以获得，其原因在于: 1. 若对象含有时滞特性； 2. 若对象模型含有右半平面(RHP)零点； 3. 若对象模型严格有理； 4. 采用理想控制器构成的系统，对于模型误差极为敏感，若模型不准确，则无法确保闭环系统的鲁棒稳定性。为了解决上述问题，在设计内模控制器时应分为两步进行: 1. 设计一个稳定的理想控制器，而不考虑系统的鲁棒性和约束; 2. 引人滤波器，通过调整滤波器的结构和参数来获得期望的动态品质和鲁棒性。
若取
，
若取
若取
，
,
第4章内模控制
为了减少突加设定值时的冲击，柔化控制动作，通常将设定值经输人滤波器后再送至控制器。经柔化后的输人参考轨迹的一般形式为:
即
第4章内模控制 4.6 简化模型预测控制（SMPC）
内模控制是一种极具理论价值的基于模型的控制策略，但其工程实现因涉及模型求逆和滤波器合理设计等问题，设计过程较为复杂，尤其是对于多输人多输出过程，实施难度更大。 1987年以后，Arulalan等人提出了一种简化模型预测控制(SMPC)，其基本思想是“系统的闭环响应至少能达到其开环响应的性能”，由此导出控制算法后，引入一个整定参数，使响应加快到比较满意的程度。
第4章内模控制一、内模控制器设计应分两步进行：
步骤1：过程模型 G p (s ) 的分解
～
步骤2：IMC控制器设计控制器设为：
低通滤波器
第4章内模控制二、内模控制器对闭环系统的影响：
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
第4章内模控制
对于模型无差，即 em ( s) 0 的特殊情况，上式可简化为：
控制器取为：设计时为保持闭环系统零稳态偏差特性，需满足：
可实现因子可取为:
第4章内模控制
下面将验证一下闭环系统输出方程是否具有零稳态偏差特性：
模型匹配时，系统闭环响应为:
第4章内模控制
若模型失配或有干扰存在时，则闭环系统不一定能获得所期望的动态性能，甚至会出现闭环系统不稳定的情况。
解决方法：在反馈通道中插人一个反馈滤波器，适当选取波器的
第4章内模控制 4.3 内模控制器设计——连续过程基本内模控制结构
• IMC→常规控制器：
GIMC ( s) Gc ( s) 1 GIMC ( s)Gm ( s)
第4章内模控制常规的反馈控制系统
• 常规控制器→IMC：
Gc ( s) GIMC ( s) 1 Gc ( s)Gm ( s)
第4章内模控制三内模控制的结构图中虚线框内是整个控制系统的内部结构，由于该结构中除了有控制器外，还包含了过程模型，内模控制因此而得名。四内模控制的特点 1. 内模控制不仅在工业过程控制中获得了成功的应用，而且表现出在控制系统稳定性和鲁棒性理论分析方面的优势。 2. 在工业过程中，内模控制用于强耦合多变量过程、强非线性过程和大时滞过程。
第4章内模控制
4.6.2.1 SMPC的稳定性
特征方程: 举例:
则等效内模控制器特征方程为:
4.6.2.2 SMPC的零稳态偏差特性 (i)对于设定值的对于干扰的阶跃响应:
结论:SMPC控制对于设定值变化和干扰变化，无论模型误差存在与否,
均无稳态误差。 4.6.2.3 SMPC的鲁棒性 ——即“模型失配对系统稳定性的影响”
第4章内模控制
4.6.2.4 SMPC不能实现对时滞的完全补偿
考虑如右对象: 对象的模型为: 闭环系统的特征方程为:
模型匹配时，闭环系统的特征方程可简化为:
第4章内模控制
4.6.3 改进的SMPC算法
对算法改进，即是改进算法的控制率。
问题：即使模型匹配，也存
在稳态偏差。
第4章内模控制
为保证系统稳定性，进一步将算法改进。
情形B.具有右半平面(RHP)零点
第4章内模控制 4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时，内模控制系统的性质仍然成立。在离散时间条件下，设计内模控制器也仍然分为两步进行：首先是设计一个稳定的理想控制器；然后在反馈和输人通道上增加反馈滤波器和输人滤波器，通过调整滤波器的结构和参数，使系统获得所期望的性能。下面就对开环稳定过程进行离散内模控制器设计。考虑一般情况，令被控对象为有纯滞后的非最小相位过程，则过程模型可分解为两部分：
第4章内模控制
4.1 引言
一内模控制内模控制(Internal Model Control, 简称IMC)是一种基于过程数学模型进行控制器设计的新型控制策略。由于其设计简单、控制性能好和在系统分析方面的优越性，内模控制不仅是一种实用的先进控制算法，而且是研究预测控制等基于模型的控制策略的重要理论基础，以及提高常规控制系统设计水平的有力工具。二内模控制的发展 1. 自20世纪50年代后期起，开始采用类似内模控制的概念来设计最优反馈控制器。 2. 1982年，完整地提出了内模控制结构，并得到工程化实现。
第4章内模控制二理想控制器特性
在理想情况下，IMC能实现对参考输人的无偏差跟踪. 然而: 1. 由于对象中常见的时滞和惯性环节，中将出现纯超前和纯微分环节，因此，理想控制器很难实现。 2. 对于具有反向特性，即包含不稳定零点的过程, 会含有不稳定极点。中将
第4章内模控制三零稳态偏差特性 1. 类型1系统若闭环系统稳定，即使模型与过程失配，即 , 只要控制器设计满足，即控制器的稳态增益等于模型稳态增益的倒数，则此系统属于类型1，且对于阶跃输入和常值干扰均不存在稳态偏差。
4.6.1 常规SMPC算法
对象开环正规化阶跃响应为:
闭环系统的设定值单位阶跃响应为:
第4章内模控制
令上述两个响应相等，即
对被控对象施加上述控制作用时，由推导过程可知，闭环系统的单位设定值阶跃响应将与正规化开环阶跃响应完全等价。
常规 SMPC
第4章内模控制
4.6.2 SMPC的性能分析（利用内模控制结构）
以上两式表明：对于无模型失配的情形，闭环传递函数除了中必须包含所有的滞后和右半平面零点，且必须有足够的阶次来避免物理上的不可实现外，其他都是可以任意选择的。因此，闭环响应可以直接设计，且设计步骤比常规反馈控制器要清楚很多。
第4章内模控制 4.3.1
～
G p (s )
的分解
(i): (ii): 对于最小相位系统：
第4章内模控制 4.2 内模控制基本原理 4.2.1 内模控制的结构及其等价形式
则系统的闭环响应为：
第4章内模控制内模控制系统的反馈信号为：
4.2.2 内模控制的主要性质一对偶稳定性当模型匹配时，IMC系统的闭环稳定性只取决于前向通道各环节的自身的开环稳定性。
内模控制稳定性条件比起经典控制理论中常用的劳斯判据、根轨迹判据和频率特性等稳定性分析方法要简单得多。与内模控制相比，传统的反馈控制结构在如何选择控制器类型和控制器参数以保证闭环系统的稳定性等间题上则显得不够清晰。

内模控制

页数:7
6.内模控制

页数:30
内模控制

页数:28
内模控制

页数:29
内模控制.ppt

页数:30
内模控制技术

页数:36
第4章内模控制

页数:30
内模控制及其仿真应用

页数:3
内模控制器设计

页数:19
基于内模控制的PID控制系统的研究与应用

页数:72

第4章内模控制

合集下载

4讲内模控制IMC与Smith预估器

内模控制

内模控制和Smith预估器

内模控制

内模控制在多电机同步驱动系统中的应用

过程控制工程智慧树知到答案章节测试2023年中国石油大学(华东)

神经网络内模控制 PPT课件

第4章_内模控制

内模控制在过程控制系统中的应用研究

内模控制和Smith预估器

内模与预测控制

内模控制与预测控制

一种基于干扰观测器的内模控制方法

1.内模概论

IMC控制

内模控制器设计

浙江大学博士入学考试线性系统控制理论真题03-09

文档推荐

最新文档

第4章 内模控制

合集下载

4讲 内模控制IMC与Smith预估器

内模控制

内模控制和Smith预估器

内模控制

内模控制在多电机同步驱动系统中的应用

过程控制工程智慧树知到答案章节测试2023年中国石油大学(华东)

神经网络内模控制 PPT课件

第4章_内模控制

内模控制在过程控制系统中的应用研究

内模控制和Smith预估器

内模与预测控制

内模控制与预测控制

一种基于干扰观测器的内模控制方法

1.内模概论

IMC控制

内模控制器设计

浙江大学博士入学考试线性系统控制理论真题03-09

文档推荐

最新文档

第4章内模控制

4讲内模控制IMC与Smith预估器