量子化学_变分法
- 格式:ppt
- 大小:300.00 KB
- 文档页数:24


变分法解薛定谔方程量子力学中的薛定谔方程是描述微观粒子的运动的基本方程之一。
薛定谔方程的解决需要使用变分法,这是一种数学方法,用于寻找使得函数取得极值的情况。
本文将介绍变分法如何应用于解薛定谔方程。
薛定谔方程描述了微观粒子的波函数随时间的演化。
它的一般形式如下:$$\hat{H}\psi = E\psi$$其中,$\hat{H}$是哈密顿算符,描述粒子的能量和势能;$\psi$是波函数,描述粒子的位置和动量分布;$E$是粒子的能量。
为了解决薛定谔方程,我们需要找到使得波函数取得极值的情况。
变分法是一种能够解决这类问题的数学方法。
首先,我们引入一个变分函数$\delta\psi$,表示波函数的微小变化。
我们的目标是找到使得$\delta\psi$为零的情况,即波函数的极值点。
为了达到这个目标,我们可以通过最小化波函数的能量来寻找波函数的极值点。
波函数的能量可以通过以下公式计算:$$E[\psi] = \int \psi^* \hat{H} \psi dV$$其中,$\psi^*$表示波函数的共轭复数,$dV$表示微元体积。
通过对能量泛函$E[\psi]$求导,并令导数为零,我们可以找到波函数的极值点。
我们首先对波函数的变分进行展开:$$\delta\psi = \sum_{n=1}^{\infty} c_n \delta\psi_n$$其中,$\delta\psi_n$是基函数的变分,$c_n$是系数。
将波函数的展开形式代入能量泛函的表达式,我们可以得到:$$E[\psi] = \sum_{n=1}^{\infty} c_n^* \int \psi_n^* \hat{H} \psi dV$$我们可以看出,能量泛函$E[\psi]$的极值点只依赖于波函数的展开系数$c_n$,而与基函数的形式无关。
因此,我们可以选择适当的基函数,将波函数展开为有限项的形式,从而简化计算。
接下来,我们对能量泛函$E[\psi]$求导,并令导数为零,即$\frac{\partialE}{\partial c_n^*} = 0$。


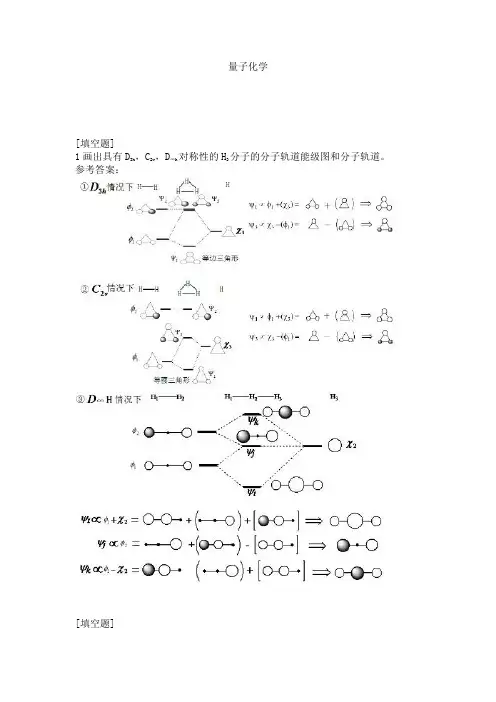
量子化学[填空题]1画出具有D3h ,C2v,D∞h对称性的H3分子的分子轨道能级图和分子轨道。
参考答案:[填空题]2用轨道相互作用解释氯代乙烷生成乙烯的机理。
参考答案:在卤代烷烃中,C-H键与C-X键处于反式构象。
C-H键能够被碱进攻,在双分子消除反应的过滤态中,碳原子上聚集了多余的负电荷,这些负电荷被用于去质子化过程,在轨道形成的过程中,弱的C-H键将电荷转移到碳上,但自身变化稳固,且形状与na键相似,这便成了单分子消除反应的中间体,由于这个C-H 键与处于反求反式构象,使有效干扰被最大化,这种作用也使电子云密度从去*轨道上,因此C-X键被削弱,最终C-X键和C-H 质子化的C原子转移到σa键被完全破坏,形成乙烯分子的键。
[填空题]3由一维谐振子的解拓展到二维、三维谐振子,理解零点能、能级简并态及波函数的奇偶性等概念。
参考答案:[填空题]4理解价键理论和分子轨道理论对H2的处理。
参考答案:在价键理论中氢分子中每个氢原子提供1个电子,两个自旋配对形成化学键,氢分子的零级波函数为价键理论中,完全没有考虑两个电子在同一原子上的结构。
高估了电子相关,可以通过引入离子-共价共振来降低电子相关作用。
分子轨道理论中,两个电子在同一原子上的结构与每个电子在不同原子上的结构同等重要,通过引入组态相互作用,可以降低离子型结构的比例。
分子轨道理论所选择的尝试波函数易实现正交性,因此便于计算,价键法中的尝试波函数难于正交,因此计算起来比较繁杂。
[填空题]5理解Hohenberg-Kohn第一、第二定律。
参考答案:1.第一定律:体系的基态能量仅仅是电子函数的泛函,即E由基态的电子概率密度ρ0(x,y,z)唯一确定。
用公式可表示为E=E(ρ)。
2.第二定律:以基态密度为变量,采用变分法将体系能量最小化之后就得到了基态能量。
[填空题]6理解高斯程序中分子构型优化的4个收敛标准。
参考答案:(1),所以力必须基本为零,此时代表势能面上的最高点或者最低点;(2)力的均方根必须基本为0,即在规定的公差范围内;(3)下一步的计算位移必须小于定义的截断值(基本为0);(4)下一步的计算位移的均方根也必须低于其截断值(基本为0)。




量子化学方法小总结12008-02-26 14:26量子化学计算方法主要分为:①分子轨道法(简称MO法);②价键法(简称VB法)。
分子轨道法,它是原子轨道对分子的推广,即在物理模型中,假定分子中的每个电子在所有原子核和电子所产生的平均势场中运动,即每个电子可由一个单电子函数(电子的坐标的函数)来表示它的运动状态,并称这个单电子函数为分子轨道,而整个分子的运动状态则由分子所有的电子的分子轨道组成(乘积的线性组合),量子计算方法主要为分子轨道常见。
分子轨道法的核心是Hartree-Fock-Roothaan方程,简称HFR方程。
1928年D.R.Hartree提出了一个将N个电子体系中的每一个电子都看成是在由其余的N-1个电子所提供的平均势场中运动的假设。
这样对于体系中的每一个电子都得到了一个单电子方程(表示这个电子运动状态的量子力学方程),称为Hartree 方程。
使用自洽场迭代方式求解这个方程,就可得到体系的电子结构和性质。
Hartree方程未考虑由于电子自旋而需要遵守的泡利原理。
1930年,B.A.Fock 和J.C.Slater分别提出了考虑泡利原理的自洽场迭代方程,称为Hartree-Fock 方程。
它将单电子轨函数(即分子轨道)取为自旋轨函数(即电子的空间函数与自旋函数的乘积)。
泡利原理要求,体系的总电子波函数要满足反对称化要求,即对于体系的任何两个粒子的坐标的交换都使总电子波函数改变正负号,而slater 行列式波函数正是满足反对称化要求的波函数。
将Hartree-Fock方程用于计算多原子分子,会遇到计算上的困难。
C.C.J.Roothaan提出将分子轨道向组成分子的原子轨道(简称AO)展开,这样的分子轨道称为原子轨道的线性组合(简称LCAO)。
使用LCAO-MO,原来积分微分形式的Hartree-Fock方程就变为易于求解的代数方程,称为Hartree-Fock -Roothaan方程,简称HFR方程。

