- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
* * * * * * * * *
*Βιβλιοθήκη TΨ x Ψ x , ,
* *
*
, w, z *T x Ψ x * , * , * , x * , w* , z * *T x * 0 ,x
即 E H x * , * , w, t H x * , * , w* , t 0
若g中不包含x,则为
(42)
H x
(43)
2) 在最优轨迹上,与最优控制u*相应的函数取
绝对极小值,即
min H x , , u, t H x , , u , t
* * * * * uU
(44)
或
H x * , * , u, t H x * , * , u * , t
Ψ Φ N T T J 1 Ψ x t f x t f t f t t f
Φ N T Ψ T T Ψ d x t f w x x t t w x f Ψ z z
Φ N T Ψ T 故 J x d x t f x x t t x f
Ψ x x
T
t t f
t f
tf
t0
Ψ d Ψ x d t (13) x d t x
Φ N T T T Ψ d x t f x x t t x x f
t t f
tf
t0
Ψ d Ψ x dt x d t x
T
注意到 d x t f x t f x t f t f
tf t0
(4)
式中,Φ和L——连续可微的矢量函数 tf——待定终端时刻。 最优控制问题就是要寻求最优容许控制u(t)在 满足上列条件下,使J为极小。
与前面讨论过的等式约束条件最优控制问题作
一比较,可知它们之间的主要差别在于:这里的控
制u(t)是属于有界闭集U,受到不等式g[x(t), x(t),t]≥0 约束。为了把这样的不等式约束问题转化为等式约 束问题,采取以下两个措施:
1) 欧拉方程
Ψ d Ψ 0 x d t x Ψ d Ψ 0 即 w d t w Ψ d Ψ 0 即 z d t z d Ψ 0 d t w d Ψ 0 d t z
(17)
(18)
(19)
2) 横截条件
Ψ Φ N T Ψ xT 0 x t f t f t t f
N xt f , t f 0
式中N——q维连续可微的矢量函数,q≤n。
(2)
控制 ut R r 受不等式约束
gxt , ut , t 0
式中g——l维连续可微的矢量函数,l≤r。
(3)
性能泛函
J Φ xt f , t f Lxt , u t , t d t
(20)
Φ N T Ψ 0 x x t t x f
(21)
Ψ w Ψ z
0
t t f
(22)
0
t t f
(23)
Ψ ,便得到 将 Ψ 代入式(17),并注意到 x
1) 欧拉方程
H g x x
的必要条件。为使最优解为极小,则还必须满足维
尔特拉斯 E 函数沿最优轨迹为非负的条件,即
E Ψ x , w , z , x, w, z Ψ x , w , z , x , w , z
* * * * * * * * *
xx
* T
Ψ w* w x
gxt , ut , t 0
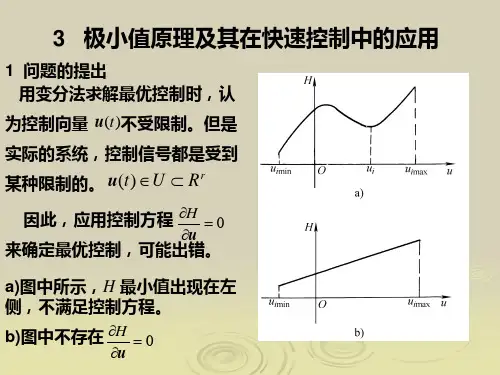
在这种情况下,控制方程 H u 0 已不成立, 所以不能再用变分法来处理最优控制问题。
一、连续系统的极小值原理
设系统状态方程为
xt f xt , ut , t
(1)
初始条件为x(t0)=x0,终态x(tf)满足终端约束方程
tf t0
(39)
取哈密尔顿函数为
H Lx, u, t f x, u, t
T
(40)
则实现最优控制的必要条件是,最优控制u*、
最优轨迹x*和最优协态矢量λ*满足下列关系式:
1) 沿最优轨线满足正则方程
H x
(41)
H g T x x
恒有
Ψ Ψ 0 w z
(32)
Ψ 3) 若将 Ψ 代入 0 ,则得 w
H g T 0 w w
即
H g T u u
这表明在有不等式约束情况下,沿最优轨迹
H 0 这个条件已不成立。 u
值得指出的是,式(24)~式(30)只给出了最优解
T
t t f
t t f
tf
t0
T Ψ d Ψ T d Ψ T d Ψ w z x d t (16) x d t x d t w d t z
由于δtf、δxT(tf)、δx、δw、δz都是任意的, 于是由δJ1=0可得增广性能泛函取极值的必要条件, 是下列各关系式成立。
(47)
5) 满足边界条件
xt 0 x0
N xt f , t f 0
这就是著名的极小值原理。
(48)
下面对定理作些说明: 1) 定理的第一、第二个条件,即式(41)~式 (44),普遍适用于求解各种类型的最优控制问题, 且与边界条件形式或终端时刻自由与否无关。其
T tf t0
(10)
现在求增广性能泛函J1的一次变分
J1 J t J x J w J z
f
(11)
式中 J t f、δJx、δJw、δJz分别是由于tf、x、w、z 作微小变化所引起的J1的变分。
J t
f
t f
Φ T N t f t f Ψ d t t f t f t t f
T
(24)
d H g T d t w w
0
(25)
d T z 0 dt
(26)
2) 横截条件
Φ N T H 0 t f t f t t f
(27)
Φ N T 0 x x t t f H g T w w 0 t t f
为简便计,令
Ψ x, x, w, , , z, t H x, w, , t T x T g x, w, t z 2
(9)
于是J1可写成
J 1 Φ xt f , t f N xt f , t f Ψ x, x, w, , , z, t d t
T
Ψ * zz w
T
Ψ 0 z
(33)
Ψ Ψ Ψ 0, 0, 和 由于沿最优轨线有 w x z
z 2 g x, w, t ,所以上式可写成 并且
Ψ x , , , x, w, z Ψ x , , , x , w , z x x
H g u u
T
(45)
沿最优轨迹,有
3) H 函数在最优轨迹终点处的值决定于
Φ T N 0 H t f t f t t f
4) 协态终值满足横截条件
(46)
Φ N T t f xt f xt f t t f
(12)
Φ N T Ψ t f t f t f t t f
T J x d x t f Φ N x
T
t t f
tf
t0
T Ψ T Ψ x x dt x x
tf t0
H x, w, , t T x T g x, w, t z 2 d t (7)
的极值问题。
哈密尔顿函数为
H x, w, , t Lx, w, t f x, w, t
T
(8)
T
Ψ J w w t f w
T
t t f
tf
t0
d Ψ w dt d t w
T
(14)
Ψ J z z t f z
T
t t f
tf
t0
d Ψ z dt d t z
T
(15)
把式(12)~式(15)代入式(11),最后得
(34)
u , * u * w 以w 代入上式,便得
H x , , u, t H x , , u , t
* * * * *
(35)
上式表明,如果哈密尔顿函数H看成 ut U 的
函数,那么最优轨迹上与最优控制u*(t)相对应的
H将取绝对极小值(即最小值)。这是极小值原理的 一个重要结论。
1) 引入一个新的r维控制变量w(t),令
wt ut , wt 0 0
(5)
虽然u(t)不连续,但w(t)是连续的。若u(t)分段 连续,则u(t)是分段光滑连续系统。