当前位置：文档之家 › 最优控制极小值原理

最优控制极小值原理

  • 格式：ppt
  • 大小：373.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

最优控制极小值原理

最优控制极小值原理

④在最优轨线末端哈密顿函数应满足
H
[
x*
(t
* f
),
(t*f
),
u*
(t*f
),
t
* f
]
[
x*
(t
* f
t f
),
t*f
]
⑤沿最优轨线哈密顿函数变化率
H[x*(t),(t),u*(t),t] H[x*(t f ),(t f ),u*(t f ),t f ]
tf t
H(x,,u, )d
定理3－2与定理3－1的区别：P61
当 t f自由时
H (x*(tt*f ),u*(tt*f ), (tt*f )) 0
第三章 极小值原理及其应用 3.1 连续系统的极小值原理
最小值原理只是最优控制所满足的必要条件。 但对于线性系统
x&(t) A(t)x(t) B(t)u(t)
，
a11(t) L
A(t)
M
O
an1(t) L
a1n (t)
g
H
x(t)
g
(t)
H
x
式中哈密顿函数 H (x, u, λ) L(x, u) λT (t)f (x, u)
② x(t) 及 (t) 满足边界条件
x(t0 ) x0
(t f ) 0
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
③哈密顿函数相对最优控制为极小值
H[x*(t), (t),u*(t)] min H[x*(t), (t),u(t)] u(t )
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
2、积分型性能指标问题
定理3-3：
min J (u) tf L[x(t),u(t)]dt

最优控制特点

最优控制特点

切换一次，设切换
2t
时间为ts，则令
0
为了求出ts，必须
首先找出状态在
1
平面上的转移轨线。
0
1
ts
tf
t
t
由 则：
设u=1，则
其中
如图(a)所示，为一组抛物线， 当K=0时经过原点[pos]
X2 s
0
t
p
若u=-1，则
X2 N
o
X1
T u=-1
为一组抛物线，如图(b)，当K1=0时过原点[NOT]
j =1，2…r
u 最优控制 *(t)是使
为极小，则：
＋１ －１ 不定
u*(t) +1
-1
奇异
t
可见：当 当
时， 时，
有确定值，正常情况 不定， 奇异情况
我们仅研究正常情况
u*(t)写成符号函数sgn{ }形式
则
j =1，2…r
向量形式：u*(t)=-sgn{q*(t)}
=-sgn{
}
⑶根据规范方程：
在证明过程中：
与H得符号与这里所定义的相反。
∴所以有的文献中也称为“极大值原理”。 3、H对u没有可微要求，因此应用拓宽。 4、 极小值原来是求取最优控制的必要条件，非充分条件。 即：满足极小值原理不一定J取极小值,需进一步判断。
一般:对于实际系统
有最优解
有唯一解
最优解
三、几种边界条件得讨论：
上面所讨论的是
控制向量约束条件: 末端状态：
g：p ×1维函数向量
目标函数：
: 自由
问题：寻求最优控制u*(t)，使系统由初态到终态， 目标函数J 为最小
❖ 步骤：应用最小值原理进行问题的求解

西工大最优控制课程 第五章 极小值原理及其应用-2

西工大最优控制课程 第五章 极小值原理及其应用-2
解得：
x1(t) 1 Rsin(t ) x2(t) Rcos(t )
消去t，得 ( x1 1)2 x22 R2
当 u(t) 1时， x1 x1 1
解得： x1(t) 1 Rsin(t ) x2(t) Rcos(t )
消去t，得 ( x1 1)2 x22 R2
两种情况下的相轨迹如图所示：
使系统从已知初始状态 x(t0 ) x0 转移到目标集中某
一终态x(tf)时，目标泛函取最小值，其中tf未知。
min J
u j (t ) 1
tf t0
dt
tf
t0,
j
1,2,, m
Hamilton函数
H[ x(t), u(t), (t), t] 1 T { f [ x(t), t] B[ x(t), t]u(t)}
U=-1
U=+1
• 最优轨线最后一段必为下列两条开关线之一
0 ( x1, x2 ) ( x1 1)2 x22 1, x2 0 0 ( x1, x2 ) ( x1 1)2 x22 1, x2 0
• 由于控制作用的切换时间为π，倒数第二段的开关线为
1 ( x1, x2 ) ( x1 3)2 x22 1, x2 0 1 ( x1, x2 ) ( x1 3)2 x22 1, x2 0
奇异最短时间控制系统
设在区间
t0
,
t
f
中，至少对一个分量，存在一个（或多
个）子区间 t1, t2
的 t t1 , t2 ，有
且t1
,
t2
j
t0
,
t
f
，使得对所有
n
qj (t ) bij [ x (t ), t]i (t ) 0

最优控制最小值原理

最优控制最小值原理
4
2-1 连续系统的最小值原理
问题 2-1 设系统的状态方程是
x f [x(t),u(t),t]
(2-1)
其中 f 是 n 维连续可微的向量函数；状态 x(t) Rn，其初态已
知是
x(t0 ) x0
终态应满足边界条件
(2-2)
[x(t f ),t f ] 0 其中 是 r 维连续可微的向量函数，r n；
tf t0
{L(x,
w,t)
T[
f
(x,
w,t)
x]
T[g(x,
w,t)
z2]}dt
(2-8)
的极值。
为 简 便 计 ， 令
H(x,,w ,t)L(x,w ,t)Tf(x,w ,t)
(2-9)
(x,x,w,w ,z,z,,,t) H(x,,w ,t)TxT[g(x,w ,t)z2]
(2-10)
8
于 是 (2-8)式 可 写 成
J(u) [x(tf)t,f]vT[x(tf)t,f]
tt0f (x,x ,w ,w ,z,z,,,t)dt
(2-11)
现 在 求 广 义 性 能 指 标 (2-11)的 一 阶 变 分 ：
JJtfJxJwJz
(2-12)
式 中 Jtf， Jx， Jw， Jz分 别 是 由 于tf ， x ， w和z的 微 变
tf t0
(x,x,w,w ,z,z,,,t)d
=0
分步积分
J w
t f
t0
(wT
w
w T
w )dt
wT
(t
)
w
t
t
f
t f wT t0
d dt
w
dt

教材第3章极小值原理

教材第3章极小值原理

（3—13） （3—14）
∫ δ J t f
=∂ ∂tf
⎢⎣⎡Φ + μ T N +
tf tf
+δ
tf
Ψdt
⎤ ⎥⎦
t=t f
δ
tf
=
⎡ ⎢ ⎢⎣
∂Φ ∂t f
+ ∂N T ∂t f
⎤ μ + Ψ⎥ δ t f
⎥⎦ t =t f
（3—15）
[ ] ∫ δ
Jx
=d
xT (t f
)∂ ∂x
Φ + μT N
dt
∫ δ
Jw
=
δ
wT
(t
f
)
∂Ψ ∂ w
t=t f
−
tf t0
δ
wT
d dt
∂Ψ ∂ w
dt
∫ δ
Jz
=δ
zT
(t f
)
∂Ψ ∂ z
t=t f
−
tf t0
δ
zT
d dt
∂Ψ ∂ z
dt
把式（3—15）～式（3—19）代入式（3—11）整理可得
（3—17） （3—18） （3—19）
δ J '=δ Jt f +δ Jx +δ Jw +δ Jz
x = f [x(t) , u(t) , t]
x(t) ∈ Rn
（3—44）
始端条件为
x(t0 ) = x0
终端约束为
（3—45）
N [x(t f ) , t f ] = 0 N ∈ Rm m ≤ n
控制约束为
，t f 待定
（3—46）
g[x(t) , u(t) , t] ≥ 0 u(t) ∈ Rr g ∈ Rl l ≤ r ≤ n

第八章 极小值原理

第八章 极小值原理
均自由。经过同变分法中的类似推导，最后得
Ja
x t x
f ，t tf
f
tf
T x
tf
x
tf t f
，t
f
H
x
tf
，u
tf
，
tf
，t f t f
tf t0
H
x，u，λ，t
x
&T
x
H
x，u，λ，t
u
T
u
H
x，u，λ，t λ
*T tbiu*i t *T tbiui t
由此可得最优控制规律为
L.S.Pontryagin
第一节 连续系统的极小值原理
设连续系统动态方程为：
x&t f xt，ut，t
(8-1)
边界条件可以固定、自由或受轨线约束，控制变量 ut 属于m维 有界闭集U，即
性能指标为：
utU Rm
(8-2)
J x
tf
，t f
tf t0
F
xt，ut，t dt
(8-3)
J x
tf
，t f
tf t0
F
xt，ut，t dt
为极小。
(8-9)
设对应于最优情况的性能指标为 J u* ，仅考虑由于 u* t 偏离 ut
时的性能指标为 J u ，则按最优的定义，下式必然成立
J u J u* J 0
设 u* t 偏离 ut 足够小 ut u* t ut
(8-10)
H x* t，u* t ，λ* t ，t c
t t0，t f
(8-31)
如果终端时刻 t f 自由，则
H x* t，u* t ，λ* t ，t 0

第七章极小值原理与典型最优控...

第七章极小值原理与典型最优控...

故极小值条件为(存在最优控制的充分条件)
Q(t), S 0, R(t) 0
31
在某些情况下，S矩阵的某些元素大到足 以引起计算上的困难，在此情况下，用 逆Riccati方程求解。
令
P(t)P1(t) I
（11）
P (t)P1(t) P(t)P 1(t) 0
（12）
P(T ) 0
P limP(t,0,T ) T
41
PI调节器
Min J 1

[
xT
(t
)Qx(t
)

u
T
(t
)
R
u(t
)

u
T
(t
)
Su
(t
)]dt
u(t)
2 t0
x(t) Ax(t) Bu(t)
s.t.
x(t0
)

x0
u *(t) K1x(t) K2u *(t)
Min J 1

[
xT
(t
)Q(t
)
x(t
)

u
T
(t
)
R(t
)u(t
)]dt
u(t)
2 t0
x(t) A(t)x(t) B(t)u(t)
s.t.
x(t0
)

x0
上述问题有解的条件：系统完全可控
u *(t) R1(t)BT (t)P (t)x(t)
38
P (t) P(t,0, ) limP(t,0,T ) T
如果 u 是最优控制律
对应于边界条件有
H[x(t), u(t), (t), t] H[x(t), v(t), (t), t], v

最优控制极小值

最优控制极小值
ɺ x= ∂H = f [ x, u , t ] ∂λ
∂H ∂L ∂ T =− − [λ f ] ∂x ∂x ∂x
(2·1—8) (2·l—9) (2·1—10)
ɺ λ=−
∂H =0 ∂u
（2·1—11） 方程(2·1—8)、(2·1—9)和(2·1—10)是利用哈米尔登函数法导 出的欧拉方程，分别叫做系统方程和控制方程。方程 (2·1—11)是相应的横截条件，式中n维矢量 λ (t )叫做协状态矢量 方程(2·1—8)和(2·1—9)一起叫做规范方程。
∂2H ∂u∂x δx dt ∂ 2 H δu 2 ∂u
(2·3—19)
和(n十m)×(n十m)矩阵， 即
∂2H 2 x ∂2 ∂ H ∂x∂u ∂2H ∂u∂x ∂2H ∂u 2
(2·3—20) 都是正定或半正定(负定或半负定)的。
tf
(2·1—14) υ 式中µ 和 分别是r维和q维的。根据泛函取极值的必要条件，J = 0 δ 可求出初始状态和终端状态受约束时的横截条件为
t0
∂Φ 2 ∂Mµ T + ]t =t0 λ (t0 ) = [ ∂x ∂x
M [ x(t 0 ), t 0 ] = 0
∂Φ1 ∂Nυ T λ (t f ) = [ + ]t =t f ∂x ∂x
t0 tf
（2.1—2） 、Φ 2 和L都是连续可微的纯量函数。假设端点时间 t 0 和 t f
t0
定义一个纯量函数
（2.1—4） 该函数称做哈米尔等函数。利用这个函数，方程(2·1—3)可写成
ɺ J ′ = Φ1[ x(t f ), t f ] − Φ1[ x(t0 ), t0 ] + ∫ {H [ x(t ), u (t ), t ] − λT (t ) x(t )}dt

最 优 控 制 教 案第三章 极小值原理及其应用

最 优 控 制 教 案第三章 极小值原理及其应用

① 正则方程
x(t
)
=
∂H ∂λ
λ(t) = − ∂H ∂x
② 横截条件
x(t0 ) = x0
Ψ ⎡⎣x(t f ),t f ⎤⎦ = 0
λ (t
f
)
=
∂ϕ ∂x(t f
)
+
∂ΨT ∂x(t f
)
V
(t
f
)
③ 在最优轨线上，与最优控制 u*相对应的 H 函数取绝对极小值
H (x*,u*, λ) = min H (x*, u, λ) u∈Ω
=
1 4
，
x1
=
u1
=
1 2
(1 +
c1 )t
−
1 2
c2
x 2
=
x1
+
1 4
x1
=
1 4
(1 +
c1)t 2
−
1 2
c2t
+
c3
x 2
=
1 4
(1 +
c1)t 2
−
1 2
c2t
+
c3
+
1 4
x2
=
1 12
(1 +
c1 )t 3
−
1 4
c2t 2
+
(c3
+
1 )t 4
+
c4
x1(0) = 0 ⇒ c3 = 0 x2 (0) = 0 c4 = 0
x1(0) = 1 ⇒ c1 = 2 ⇒ x1 = 2e−t −1
x2 (0) = 0 c2 = 2
x2 = −2e−t − t − 2

最优控制 第四章 极小值原理及其应用2

最优控制 第四章 极小值原理及其应用2
0 或:
)( * ) ( * )(z z * ) 0 * z
0
T
T ) ( x x* ) x
-λ
*
E ( x* , x, , z , * , * , t ) * x { ( x* , x* , * , z * , * , * , t ) * x*} H ( x* , * , , t ) H ( x* , * , * , t ) 0 H ( x* , * , u , t ) H ( x* , * , u * , t )
第四章 极小值原理及其应用
用古典变分法解最优控制问题时,假定u(t)不受限制,从而得到最优控制应满足
H 0 u
实际上在工程问题中,控制变量总有一定的限制.
设控制变量被限制在某一闭集内 即u(t)满足 G[ x(t ), u (t ), t ] 0
u
满足限制条件的u(t)称为容许控制，由于δu不能是任意的,
H 0 u
这一条件不成立,而代之以与最优控制相对应的函数为绝对极小,其次是正则 方程略有改变,仅当G中不包含x时, 方程才不改变.
11
当 t0和x(t0)给定,根据tf给定或自由, x(tf)给定,自由或受约束等不同情况下所导 出的最优解必要条件列表如下: 终 端 状 态 固
性能指标
正则方程
12
性能指标
终 端 状 态
正则方程
极值条件
边界条件与横 截条件
x ( t 0 ) x0 x (t f ) x f

tf 给 定
tf
t0
J 固 F [ x, u , t ]dt
定 自 由
H H x G ( )T x H F ( x, u , t ) T f ( x, u , t ) x 若 G (u , t ) 0 H 则 x

最优控制第六章极小值原理

最优控制第六章极小值原理

以 w u，w * u*代入上式，便得
H x*, *,u,t H x*, *,u*,t
(35)
上式表明，如果哈密尔顿函数H看成 utU 的
函数，那么最优轨迹上与最优控制u*(t)相对应的
H将取绝对极小值(即最小值)。这是极小值原理的
一个重要结论。
定理 设系统状态方程为
xt0 x0
Nxt f ,t f 0
(48)
这就是著名的极小值原理。
下面对定理作些说明： 1) 定理的第一、第二个条件，即式(41)～式
(44)，普遍适用于求解各种类型的最优控制问题， 且与边界条件形式或终端时刻自由与否无关。其
中，第二个条件：min H x*, *,u,t H x*, *,u*,t uU
(45)
u u
3) H函数在最优轨迹终点处的值决定于
H

Φ
T
N

0
(46)
t f
t f tt f
4) 协态终值满足横截条件
t f
Φ


x
t
f
N T
x t f


tt f
(47)
5) 满足边界条件
J1

Ψ

x T
Ψ x

Φ t f

N T t f


tt f
t f
d xT
tf
Φ

x

N T x


Ψ x
t t
f
wT
Ψ w tt f
zT
Ψ z
tt f

最优控制第2章 极小值原理

最优控制第2章 极小值原理

2015-03-24
20
u
*
(t
)
=
⎧ −1, ⎪⎨−0.5λ2
(t
λ2 (t ), | λ2
)> (t)
2 |≤
2
(∗)
⎪⎩ 1, λ2 (t) < −2
由伴随方程 λ& = −∂H / ∂x 得到：
求解得到：
λ&1(t) = 0, λ&2 (t) = −λ1(t)
λ1(t) = c1, λ2 (t) = −c1t + c2 本例tf自由，因此H函数在最优终端时刻 t*f满足横截条件:
2015-03-24
17
分分析析::
要使 H[x*, u, λ*, t] 达到极小，就要 (1 − λ*)u达到极小 。由控 制约束 0.5 ≤ u ≤ 1 可得，最优控制为：
u *(t)
=
⎧ 1, ⎨⎩0.5,
λ >1 λ <1
由 λ (t) = e1−t − 1易知，当ts=0.307时，λ * (ts ) = 1 ，故最优 控制为：
2015-03-24
3
定理１（极小值原理）对于上述最优控制问题，选取哈密 顿函数为：
H = L( x,u,t) + λT (t) f [x(t), u(t), t]
则实现最优控制的必要条件：
(1) 最优状态x*和最优协态 λ* 满足正则方程:
x&(t) =
∂H ∂λ
=
f [ x(t), u(t), t]
则伴随方程 λ& = −∂H / ∂x为：
λ& = − ∂H = −1 − λ ∂x
15
2015-03-24

现代控制理论 第6章 最优控制(录像)2(极小值 [1]加了二次型

现代控制理论 第6章 最优控制(录像)2(极小值 [1]加了二次型
由min H x , ,u,t H x , ,u ,t uU
min H
uU
min uT BT
u( t ) SGN( BT )
得：
ui( t )sgn ( BT ) i ,i1,2, ,r
1 a 0
其中函数sgn a
0
a0
1 a 0
a为向量时用SGN表示。
总目录 返回 上一页 下一页
6.8 极小值原理
经典变分法
x Hx,u, ,t , Hx,u, ,t , Hx,u, ,t 0
x
u
状态方程
伴随方程
控制方程
应用范围：
u无约束, 且H对u连续可微 难满足
一般 ui Mi ( i 1,2 m ) 更一般控制u(t)受不等式约束：
gxt ,u(t),t 0
总目录 返回 上一页 下一页
t
u 切换时刻
总目录 返回 上一页 下一页
6.10.2 状态轨线及开关曲线
x* t 12.3
1
0 0.307
1
0.5
t 0 0.307
6.44
5
1 t 0 0.307 1 t
总目录 返回 上一页 下一页
例6.8.2 已知系统 x1t x1t ut x10 1
x2 t x1t
x2 0 0
其中 ut 1 ，若x t f 自由，求u* t 使
J x2 1 min
由正则方程组： x Ax Bu
H AT
x
(
t
)
e
AT t
(
0
)
e
AT t 0
u( t ) SGN( BT ) SGN( BT e ATt0 )
1.时间控制是Bang-Bang控制,即开关控制；

最优控制（最小值原理）1

最优控制（最小值原理）1

最优控制最优控制——————最小值原理最小值原理七 几种典型的几种典型的工程工程工程应用应用 1．时间最优控制时间最优控制问题，是可以运用极小值原理求解的一个常见的工程实际问题。

如果性能指标是系统有初态转移到目标集的运动时间，则使转移时间为最短的控制称为时间最优控制，或称最速控制。

本节主要介绍线形定常系统的时间最优控制分析法及其应用。

1.1 一类非线性系统的时间最优控制先把需要解决的问题叙述如下：[问题3-1] 移动目标集的一类非线性系统的时间最优控制问题为()1min ,1,2,,fj t u t t J dt j m ≤==∫⋯..s t ① [][]00()(),(),(),()xt f x t t B x t t u t x t x =+=ɺ ② (),0f f x t t ψ =式中()n x t R ∈，()m u t R ∈；()f •和()B •维数适当，其各元对()x t 和t 连续可微；移动目标集()r R ψ•∈，其各元对()f x t 和f t 连续可微，f t 是状态轨线与移动目标集相遇的末端时刻。

显然，问题3-1属于时变条件、积分型性能指标、f t 自由和末端约束的最优控制问题。

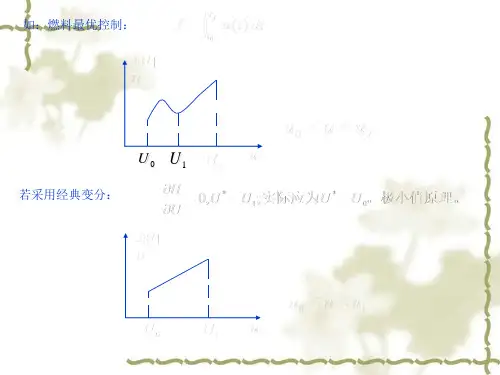
根据极小值原理，令哈密顿函数[][]{}(,,,)1()(),(),()T H x u t t f x t t B x t t u t λλ=++ （3-136）正则方程为：[][]()(),(),()Hxt f x t t B x t t u t λ∂==+∂ɺ （3-137） [](),()()()()()TTB x t t u t H ft t t x xx t λλλ ∂∂∂=−=−−∂∂∂ɺ （3-138）边界条件及横截条件为00()x t x = （3-139）(),0f f x t t ψ = （3-140）()()T f f t x t ψλγ∂=∂ （3-141）极小值条件：***1()(),()(),()T T t f x t t t B x t t u t λλ ++{}**1min 1()(),()(),()j T T u t f x t t t B x t t u t λλ≤ =++ 或者[]{}*1()(),()min ()(),()j T T u t B x t t u t t B x t t u t λλ≤ = （3-142）因而得：**()sgn (,)()T u t B x t t λ =− （3-143）式中sgn()•为符号函数。

基于古典变分法和极小值原理推导最优控制的解析求解条件

基于古典变分法和极小值原理推导最优控制的解析求解条件

基于古典变分法和极小值原理推导最优控制的解析求解条件基于古典变分法和极小值原理推导最优控制的解析求解条件引言：最优控制理论是数学和工程学交叉的一个重要领域，在各个工程领域都有广泛的应用。

它的目标是通过优化方法寻找使系统指标达到极值的控制策略。

在这个领域中，变分法和极小值原理是两个重要的数学工具。

本文将介绍古典变分法和极小值原理，以及如何利用它们推导最优控制的解析求解条件。

一、古典变分法的基本原理古典变分法是研究极值问题的一种有效数学方法。

它的核心思想是将待求函数看作一族函数的极限形式，然后通过对这族函数进行泛函求导来获得包含待求函数的微分方程。

在最优控制问题中，我们希望找到一个控制策略，使系统的目标函数达到最小值或最大值。

通过应用古典变分法，我们可以将这个极值问题转化为一个泛函极值问题，并通过求解泛函极值问题来得到最优控制。

在使用古典变分法进行最优控制问题的分析时，我们需要定义一个泛函，即系统的目标函数。

泛函通常形式如下：\[ J[y,u] = \int_{t_0}^{t_f} L(t, y(t), u(t)) dt \]其中，\[y(t)\] 是状态变量，\[u(t)\] 是控制变量，\[L(t, y(t), u(t))\] 是泛函的被积表达式，它描述了系统的动力学以及待求函数的影响因素。

二、极小值原理极小值原理是古典变分法中的一个基本概念，用于推导变分问题的最优性条件。

对于一个给定的泛函\[J[y,u]\]，如果它的极小值存在且为唯一解，那么这个极小值必须满足极小值原理的条件。

极小值原理的一般形式可以表示为：\[ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{y}}\right) -\frac{\partial L}{\partial y} = 0 \]\[ \frac{\partial L}{\partial u} = 0 \]这两个条件是极小值原理的必要条件。

5 最优控制-极小值原理

5 最优控制-极小值原理
* j
正常（或平凡）情况、奇异（或非平凡） 正常（或平凡）情况、奇异（或非平凡）情况
Bang-Bang控制原理 控制原理 是问题3 的时间最优控制, 设 u * ( t ) 是问题3-1的时间最优控制,
λ x* ( t )， ( t )
是相应的状态向量和协态向量,若问题是正常的, 是相应的状态向量和协态向量,若问题是正常的,则几乎所有 ),有下式成立 t ∈ t0 , t f (除去有限个开关时间),有下式成立 除去有限个开关时间),
在最优轨线末端哈密尔顿函数应满足的条件 (5)极值条件 极值条件
1 + λ T ( t ) f x* ( t ) , t + λ T ( t ) B x * ( t ) , t u * ( t ) =
{1 + λ T ( t ) f x* ( t ) , t + λ T ( t ) B x* ( t ) , t u * ( t )} min
u∈U
（50） ） （51） ） （52） ）
或者
H ( x * , u* , λ* , t ) ≤ H [ x * , u, λ* , t ]
哈密顿函数沿最优轨线随时间的变化规律： 哈密顿函数沿最优轨线随时间的变化规律：
* * 在末值时刻 t f 是固定的情况 H (t ) = H (t f ) = const * *
3 极小值原理及其在快速控制中的应用
1 问题的提出 用变分法求解最优控制时， 用变分法求解最优控制时，认 不受限制。 为控制向量 u(t )不受限制。但是 实际的系统， 实际的系统，控制信号都是受到
u(t ) ∈ U ⊂ R r 某种限制的。 某种限制的。
因此， 因此，应用控制方程 ∂H = 0

第六章 极小值原理(20121020)

第六章 极小值原理(20121020)
*
设有控制变量 u t ，在时间区间 t ，t 内只能在容许范围内变化， u* t（见图6-1）， 如图6-1所示。设对应取极小时之最优控制为 它由三个区间组成：
0 f
u* t0，t1 及 t 0，t f 区间内， t 处在容许集内，由于 u可以任 ⑴ 在
第二节 离散系统的极小值原理
设离散系统状态方程为：
x k 1 f x k ，u k ，k ，k 0, 1, ，N 1
u x 这里， k 为n维状态向量， k 为m维控制向量，k为步数，N 为总参数。设初始状态 x 0 x0 ，终端状态 x N 自由。控制 变量受限制，即 uk U
(6-17)
根据泛函存在极值的必要条件的结论可知，当 u t 不受限制时， 应满足 (6-18) Ja 0
由于各个变量的变分是独立的，因此，必须同时满足
协态方程：
状态方程： 控制方程： 横截条件：
H x*，u*，λ*，t x
H x*，u*，λ*，t λ
系统的性能指标为：
J x N ，N F x k ，u k ，k
k 0 N 1
* 要求寻找最优控制序列 u k ，使性能 J 为极小。
我们同样可用极小值原理来求解最优控制问题。首先，用拉 格朗日乘子法建立增广指标泛函
J x N ，N F x k ，u k ，k
* * * * * t2
t1
(6-29)
H x*，u，λ *，t H x*，u*，λ *，t dt t1 0
t2
显然，这与 J a 0 矛盾。同时，小区间t1，t2 可能出现在 t ，t 区间的任何位置，因此要求整个区间 t ，t 内均满足以下条 件

11讲 最优控制-极小值-总结及习题讲解

11讲 最优控制-极小值-总结及习题讲解

能源与动力学院系统控制与仿真研究室
16
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理
能源与动力学院系统控制与仿真研究室
17
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理

极小值原理与变分法求最优控制的比较
能源与动力学院系统控制与仿真研究室
18
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理
33
最优控制——极小值原理 3.4 极小值原理的典型应用

月面软着陆问题
h
v g
月球
能源与动力学院系统控制与仿真研究室
34
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
35
最优控制——极小值原理 3.4 极小值原理的典型应用

时间-燃料最优控制
能源与动力学院系统控制与仿真研究室
能源与动力学院系统控制与仿真研究室
7
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理
能源与动力学院系统控制与仿真研究室
8
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理
能源与动力学院系统控制与仿真研究室
9
最优控制——极小值原理 最 控制 值原 3.2 连续定常系统极小值原理
能源与动力学院系统控制与仿真研究室
27
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
28
最优控制——极小值原理 3.4 极小值原理的典型应用
能源与动力学院系统控制与仿真研究室
29
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(t f ) 0
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
③哈密顿函数相对最优控制为极小值 H [ x* (t ), (t ), u* (t )] min H [ x* (t ), (t ), u (t )]
u ( t )
④哈密顿函数沿最优轨迹线保持为常数
当 t f 固定时 H ( x* (t ), u* (t ), (t )) H ( x* (t f ), u* (t f ), (t f )) const 当 t f 自由时
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
说明： 1）极小值原理给出的只是最优控制应该满足的必要条件。 2）极小值原理与用变分法求解最优问题相比，差别仅在于极 值条件。 3）非线性时变系统也有极小值原理。
第三章 极小值原理及其应用 3.1 连续系统的极小值原理
例 3.2 重解例 3.1
0.307
t ( 4 . 37 e 1)dt 8.68
1
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
END 谢谢
0 t 0.307
0.307 t 1
t 4 e 1 * x (t) t 4.37 e 0.5
0 t 0.307
0.307 t 1
t
1.72
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
u*
1
0 .5
1
0 0.307 1
t
6.44
u 受约束。 解：定常系统、积分型t f 固定，末端自由， 取哈密顿函数
H x u x u x1 1 u
1 1 u t 0.5 1
*
注：控制的切换点为λ(ts)=1
H 1 x
1
由协态方程 由边界条件
t

t cet 1
1 ce 1 0 c e
t e1t 1
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
ts 1 0 控制的切换时间： ts 0.307
控制的切换点处
ts e
满足下述正则方程: x (t )
H
(t )
H x
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
式中哈密顿函数
H ( x, u, ) T (t ) f ( x, u)
② x(t ) 及 (t )
满足边界条件
x(t0 ) x0
(t f )
二.自由末端的极小值原理
定理3-1：对应如下定常系统、末值型性能指标、末端自由、控制受约束 的最优控制问题 min J (u ) [ x(t f )]
u ( t )
s.t.
x(t ) f ( x, u ),
x(t0 ) x0 , t [t0 , t f ]
对于最优解和最优末端时刻、最优轨线，存在非零的n维向量函数 (t )使 ① x(t ) 及 (t )
① x(t ) 及 (t ) 满足下述正则方程:
x (t ) H
t [t0 , t f ], t f 未知
H x
(t )
式中哈密顿函数
H (x, u, λ) L( x, u) λ T (t )f (x, u)
② x(t ) 及 (t ) 满足边界条件
x(t0 ) x0
x(t f )
③哈密顿函数相对最优控制为极小值
H ( x* , u* , ) min H ( x* , u, )
u ( t )
④哈密顿函数沿最优轨迹线保持为常数 当 t f 固定时
H ( x* (t ), u* (t ), (t )) H ( x* (t f ), u* (t f ), (t f )) const
第三章 极小值原理及应用
3.1 连续系统的极小值原理 3.2 离散系统的极小值原理 3.3 时间最优控制 3.4 燃料最优控制 3.5 时间-燃料最优控制 小 结
第三章 极小值原理及其应用 3.1 连续系统的极小值原理
一.问题的提出
用变分法求解最优控制时，认
为控制向量 u(t )不受限制。但是
实际的系统，控制信号都是受到 某种限制的。u(t ) U
当控制有约束时，H / u 0
* * * 不再成立，而代之为 H ( x (t ), u (t ), (t )) H ( x (t ), u(t ), (t )) u ( t )
极小值原理的重要意义：（P51) （1）容许控制条件放宽了。 （2）最优控制使哈密顿函数取全局极小值。 （3）极小值原理不要求哈密顿函数对控制的可微性。 （4）极小值原理给出了最优控制的必要而非充分条件。
当
t f 自由时
H ( x* (tt*f ), u* (tt*f ), (tt*f )) 0
第三章 极小值原理及其应用 3.1 连续系统的极小值原理
最小值原理只是最优控制所满足的必要条件。 但对于线性系统
x(t ) A(t ) x(t ) B(t )u(t )
，
a11 (t ) A(t ) an1 (t )
H ( x* (tt*f ), u* (tt*f ), (tt*f )) 0
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
例3-2：x t x t u t x 0 5
0.5 u t 1 1 * * u 试求：J 时的 ， x x t u t dt J min 0
1ts 1 1

1 * u t 0.5
0 t 0.307
0.307 t 1
0 t 0.307
代入状态方程得
xt 1 t x xt 0.5
0.307 t 1
根据边界条件继续求出：
c1et 1 xt t c2e 0.5
④在最优轨线末端哈密顿函数应满足
* * * * H [ x* (t * ), ( t ), u ( t ), t f f f f] * [ x* (t * ), t f f]
⑤沿最优轨线哈密顿函数变化率
* * * *
t f
tf
H [ x (t ), (t ), u (t ), t ] H [ x (t f ), (t f ), u (t f ), t f ]
0
12.3
0.307
1
t
x* t
5
0
0.307
1
t
最优性能指标为：
1 *
第3章 极小值原理及其应用 3.1 连续系统的极小值原理

0
J x* t u * t dt
0.307

(4e 2)dt
t 0
例3-3： 做法与前面得一样，引入两个拉格朗日乘子向量，构造广义泛函 ，在满足末端约束条件下，泛函取得极值是等价的。 3、末端受约束的情况 定理3-4:（定常系统)(P68) 定理3-5:（时变系统)(P69) 4、复合型性能指标情况 定理3-6： 表3-1,3-2（P73-74）
哈密顿函数
， ，
H x(t ) (t )( x(t ) u(t )) (1 ) x(t ) u(t )
伴随方程
(t )
H (t ) 1 x
(1) 0
由极值必要条件，知
1 0 u sign 1 0
J xdt 2e1 1
0 1

t
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
二、极小值原理的一些推广形式 1、时变问题
定义：描述最优控制问题的相关函数显含时间，称为时变问题。 解决办法：引入新状态变量，将时变问题转为定常问题，利用定理 3-1。 定理3-2： min J (u ) [ x(t f ), t f ]
a1n (t ) ann (t )
b1 (t ) B (t ) bn (t )
最小值原理也是使泛函取最小值得充分条件。
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
上述极小值原理与变分法主要区别在于条件③。
当控制无约束时，相应条件为 H / u 0 ；
定理3－2与定理3－1的区别：P61
t
H ( x, , u, ) d
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
2、积分型性能指标问题 定理3-3：
u ( t )
min J (u) L[ x(t ), u(t )]dt
t0
tf
s.t. x(t ) f ( x, u, t ), x(t0 ) x0
0 t 1
又
(t ) 1 e t 1 0
于是有
u (t ) 1
第3章 极小值原理及其应用 3.1 连续系统的极小值原理
u (t )
协 态 变 量 与 控 制 变 量 的 关 系 图
，
(t ) x(t ) 1 x x(0) 1
x (t ) 2e 1
u ( t )
s.t. x(t ) f ( x, u, t ), x(t0 ) x0
① x(t ) 及 (t ) 满足下述正则方程:
x (t ) H
t [t0 , t f ], t f 未知
H x
(t )
T 式中哈密顿函数 H ( x, , u, t ) (t ) f ( x, u, t )
第3章 极小值原理及其应用 3.1 连续系统的极小值原理