当前位置：文档之家 › 第八章 极小值原理

第八章 极小值原理

  • 格式：ppt
  • 大小：1.12 MB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

离散系统的极小值原理

离散系统的极小值原理

u * (k ) = 0.2
x* (k ) = 1 − 0.2k
k = 0,1, 2,3, 4,
总结 应用离散欧拉方程求解等式约束和不等式约束 的离散极值问题比较麻烦，而用离散极小值原理处 理这种约束问题却很方便。特别是，当控制序列受 约束时，离散变分法不再适用，只能用离散极小值 原理或离散动态规划来求解离散极小值问题。
2 离散极小值原理
庞特里亚金发表极小值原理时，只讨论了连续系 统的情况。为了获得离散系统的极小值原理，有 人曾经从离散系统与连续系统比较接近这一事实 出发，设想把连续极小值原理直接推广到离散系 统中去，但除了采样周期足够小的情况外，结果 是失败的。 离散极小值原理的普遍论述比较复杂，证明过程 也十分冗长。为了简单起见，下面介绍控制向量 序列不受约束情况下的离散极小值原理，然后不 加证明地推广到控制向量序列受约束的情况。
因为： ∂Lk = λ (k + 1)
∂x(k )
∂Lk = u (k ) + λ (k + 1) ∂u (k )
∂Lk −1 = −λ ( k ) ∂x(k )
所以由离散欧拉方程（3-6）可得：
λ ( k + 1) = λ ( k ) = c
u ( k ) = −λ ( k + 1) = −c
其中 c为待定的常数。 将 u (k ) = −c 代入状态差分方程，有
离散极小值原理可以叙述如下： 定理3 [定理3-7] （关于离散系统末端状态受约束） [定理3-8] （关于离散系统末端状态自由） 定理3
[定理3-7] 定理3 7]（关于离散系统末端状态受约束） 设离散系统状态方程
x(k + 1) = f [ x(k ), u (k ), k ]

极大极小原理

极大极小原理

极大极小原理1在“假设发生如下事情”之前，祝福我们此生永不发生这类事情。

假设你外出时，遭遇绑架，该怎么办？有一位（国外的）自卫专家，给出了三个应对原则：1、不要跟他去第二个地点。

如果你心怀侥幸，他可能将你带到偏僻的地方，为所欲为，甚至下毒手，然后掩藏他的罪恶痕迹。

2、记住，他在撒谎。

不管坏人说多好听，别相信。

这位专家的观点是：从一开始，每个谋杀犯，绑架犯，强奸犯，他们都会用同一句话：“照我说的做，我就不会伤害你。

”然而，一旦你照他们说的做，最后受伤最深的，还是你。

3、要在原地，用尽一切手段与之搏斗。

这一点似乎有点儿让人疑惑，万一受伤呢？被人用刀抵住，拼命挣扎要是不幸丢了命，岂非不识时务？然而，这位专家的洞见是：如果他们想在原地杀你，你早就已经死了。

所以：•他们不想在原地杀你，他们希望带你去其他地方，或者先干点别的事。

•通过打乱他们的计划，你会成为他们最恐怖的噩梦。

•如果他们不想被抓，不想把事搞得太麻烦，他们可能就会直接逃跑了。

以上三点原则的所有原因，其实只有一个：如果你进了他的车，或者跟着他们去了某个地方，你死定了。

（以上经验仅供参考，不构成本文作者对遇到绑架的具体建议。

）2以上是一个生动的博弈场景。

由此引出我的一句“大脑碎片”：好的一手棋，是其令对手有不好的下一手，以及自己有好的下下一手棋。

我们姑且不讨论，在第1节里，专家应对绑架的三点原则的适用范围，以及如何根据情境调整策略。

本文的焦点是：极大极小原理。

绑架，是一场零和博弈。

就像下棋，一个人赢，一个人输，即使和棋，也只是暂时的平静。

双方没有合作的可能。

对于这类博弈，冯·诺依曼提出了“极小极大原理”。

《囚徒的困境》一书，用我们熟悉的分蛋糕来示例。

众所周知，公平的分法是：一个人切，一个人选。

假如两个孩子都不是孔融，并且都想吃更多蛋糕，这其实是一个典型的零和博弈。

•第一个孩子（切蛋糕那个）的两个策略是：不均分和尽可能均分。

•第二个孩子（挑蛋糕那个）也有两个策略：选较大的那一块或选较小的那一块。

5 最优控制-极小值原理

5 最优控制-极小值原理
* j
正常（或平凡）情况、奇异（或非平凡） 正常（或平凡）情况、奇异（或非平凡）情况
Bang-Bang控制原理 控制原理 是问题3 的时间最优控制, 设 u * ( t ) 是问题3-1的时间最优控制,
λ x* ( t )， ( t )
是相应的状态向量和协态向量,若问题是正常的, 是相应的状态向量和协态向量,若问题是正常的,则几乎所有 ),有下式成立 t ∈ t0 , t f (除去有限个开关时间),有下式成立 除去有限个开关时间),
在最优轨线末端哈密尔顿函数应满足的条件 (5)极值条件 极值条件
1 + λ T ( t ) f x* ( t ) , t + λ T ( t ) B x * ( t ) , t u * ( t ) =
{1 + λ T ( t ) f x* ( t ) , t + λ T ( t ) B x* ( t ) , t u * ( t )} min
u∈U
（50） ） （51） ） （52） ）
或者
H ( x * , u* , λ* , t ) ≤ H [ x * , u, λ* , t ]
哈密顿函数沿最优轨线随时间的变化规律： 哈密顿函数沿最优轨线随时间的变化规律：
* * 在末值时刻 t f 是固定的情况 H (t ) = H (t f ) = const * *
3 极小值原理及其在快速控制中的应用
1 问题的提出 用变分法求解最优控制时， 用变分法求解最优控制时，认 不受限制。 为控制向量 u(t )不受限制。但是 实际的系统， 实际的系统，控制信号都是受到
u(t ) ∈ U ⊂ R r 某种限制的。 某种限制的。
因此， 因此，应用控制方程 ∂H = 0

极小值原理

极小值原理

极小值原理
极小值原理是数学分析中一个重要的概念。

它指出，如果一个函
数在局部区域的某点取得极小值，那么在该点的导数必须为零或不存在。

这一原理可以帮助我们研究函数的极小值以及局部极值点的性质。

具体而言，设函数f(x)在闭区间[a, b]上连续，在开区间(a, b)上可导。

如果f(x)在某点x0处取得极小值，那么f'(x0) = 0或者
f'(x0)不存在。

这是因为在极小值点处的导数为零或不存在，否则在
导数不为零的点附近将会存在更小的函数值。

利用极小值原理，我们可以通过求解导数为零或不存在的方程来
找到函数的极小值点。

此外，极小值原理还有助于我们确定函数的最
小和最大值的存在性。

总而言之，极小值原理是一条重要的数学原理，可以帮助我们研
究函数在局部区域内的极小值和极值点的性质。

极端原理在函数最值问题中的应用

极端原理在函数最值问题中的应用

极端原理在函数最值问题中的应用
极值原理是微积分中的一个重要概念，可以用来解决函数的最值问题。

对于一个连续函数f(x)，如果在闭区间[a,b]内，函数在某些点取得最大值或最小值，那么这些点要么是函数在a和b处的极值点，要么是函数在该闭区间内存在的端点。

通过极值原理，我们可以确定函数的最值点在哪里，进而找到函数的极大值和极小值。

我们需要确定函数的定义域。

对于一个给定的函数，我们需要确定它的自变量x的取值范围。

在定义域内，我们可以找到函数的最大值和最小值。

极值原理的一般步骤如下：
1. 确定函数的定义域：确定函数的自变量x的取值范围。

2. 求函数的导数：对于给定的函数f(x)，我们可以求它的导数f'(x)。

3. 解方程f'(x)=0：求解导数f'(x)等于0的方程，解得的解即为函数的驻点。

4. 计算端点值：计算函数在闭区间[a,b]的端点a和b处的值f(a)和f(b)。

5. 对比计算结果：对比驻点的函数值f(x)和端点的函数值f(a)和f(b)，找出其中最大值和最小值。

需要注意的是，有些函数可能在驻点处取得极值，但不是在函数的定义域内。

在这种情况下，驻点不是函数的最值点。

极端原理在函数最值问题中的应用非常广泛。

我们可以使用极值原理来帮助我们优化函数的性能、最小化成本或者最大化利润。

在微积分中，极值原理是一种基本的概念，也是更复杂的微积分和优化问题的基础。

理解和应用极值原理对于学习微积分和应用数学非常重要。

现代控制理论极小值原理

现代控制理论极小值原理

则使性能指标 J 达到极小的最优控制 u* t及最优状态轨线 x* t 必须满足以下条件：
⑴ 正则方程
x&* t H
a
(8-4)
&* t H
a
(8-5)
这里，H 为哈密尔顿函数， 为协态变量，其定义与在变分法中 相同。
⑵ 哈密尔顿函数对应最优控制时为极小值，即：
min
uU
H
x&*
t
，u
L.S.Pontryagin
第一节 连续系统的极小值原理
设连续系统动态方程为：
x&t f xt，ut，t
(8-1)
边界条件可以固定、自由或受轨线约束，控制变量 ut 属于m维 有界闭集U，即
性能指标为：
utU Rm
(8-2)
J x
tf
，t f
tf t0
F
xt，ut，t dt
(8-3)
T
x&
λ
dt
(8-17)
根据泛函存在极值的必要条件的结论可知，当 u t 不受限制时，
应满足
Ja 0
(8-18)
由于各个变量的变分是独立的，因此，必须同时满足
H x*，u*，λ*，t λ&* 0 x
(8-19)
H x*，u*，λ*，t x&* 0 λ
H x*，u*，λ*，t 0 u
均自由。经过同变分法中的类似推导，最后得
Ja
ห้องสมุดไป่ตู้
x t x
f ，t tf
f
tf
T x
tf
x
tf t f
，t
f
H
x
tf
，u

最小值原理的应用

最小值原理的应用

最小值原理的应用1. 简介最小值原理是指在某个范围内，存在一个函数的极小值点。

这个原理被广泛应用于各个领域，如优化算法、物理学、经济学等。

2. 优化算法最小值原理在优化算法中起到重要作用，尤其是在参数优化、模型训练等方面。

以下是几种常见的优化算法：•梯度下降法：通过计算目标函数的梯度来找到使得目标函数最小化的参数。

该算法在机器学习中被广泛应用。

•遗传算法：通过模拟生物进化过程，不断地筛选和交叉优秀个体，最终找到最优解。

•粒子群优化算法：模拟鸟群觅食的行为，通过追踪历史最优解和群体共享信息，逐步优化目标函数。

•模拟退火算法：类似于金属冶炼的过程，通过不断降温和摇动，使得系统从局部最优解逐渐走向全局最优解。

3. 物理学中的最小值原理在物理学中，最小值原理有着广泛的应用。

•波的传播：根据最小时间原理，光线在介质中的传播路径是使得光程或时间最小的路径。

这个原理在光学中起到了重要的作用。

•哈密顿原理：根据哈密顿原理，自然界的运动现象是通过使作用量取极小值的路径来实现的。

这个原理是解释物理现象的基础。

•等速面原理：根据等速面原理，自由表面上的液体分子所受到的作用力平行于液体表面，使得液体表面能量最小化。

4. 经济学中的最小值原理最小值原理在经济学中也有广泛的应用。

•边际效应原理：边际效应原理指出，在经济学中，个体在满足基本需求后，会通过比较边际效益和边际成本来做出决策。

这个原理在市场调节和资源配置中起到了重要作用。

•帕累托最优：帕累托最优是指在不损害任何一方利益的前提下，通过资源的重新配置使得至少有一方的利益得到改善。

这个原理在经济学中被广泛应用，用于分配公共资源和解决不平等问题。

•机会成本原理：机会成本原理指出，资源的使用具有代价，每选择一种用途就放弃了其他可能的用途。

这个原理在经济决策中起到了重要作用。

5. 总结最小值原理是一种广泛应用于各个领域的原理，在优化算法、物理学和经济学等领域中都有重要作用。

通过运用最小值原理，我们可以找到目标函数的最小值点，从而提高效率、减少成本、优化资源分配等。

第八章 极小值原理

第八章 极小值原理
均自由。经过同变分法中的类似推导，最后得
Ja
x t x
f ，t tf
f
tf
T x
tf
x
tf t f
，t
f
H
x
tf
，u
tf
，
tf
，t f t f
tf t0
H
x，u，λ，t
x
&T
x
H
x，u，λ，t
u
T
u
H
x，u，λ，t λ
*T tbiu*i t *T tbiui t
由此可得最优控制规律为
L.S.Pontryagin
第一节 连续系统的极小值原理
设连续系统动态方程为：
x&t f xt，ut，t
(8-1)
边界条件可以固定、自由或受轨线约束，控制变量 ut 属于m维 有界闭集U，即
性能指标为：
utU Rm
(8-2)
J x
tf
，t f
tf t0
F
xt，ut，t dt
(8-3)
J x
tf
，t f
tf t0
F
xt，ut，t dt
为极小。
(8-9)
设对应于最优情况的性能指标为 J u* ，仅考虑由于 u* t 偏离 ut
时的性能指标为 J u ，则按最优的定义，下式必然成立
J u J u* J 0
设 u* t 偏离 ut 足够小 ut u* t ut
(8-10)
H x* t，u* t ，λ* t ，t c
t t0，t f
(8-31)
如果终端时刻 t f 自由，则
H x* t，u* t ，λ* t ，t 0

极小值原理——精选推荐

极小值原理——精选推荐

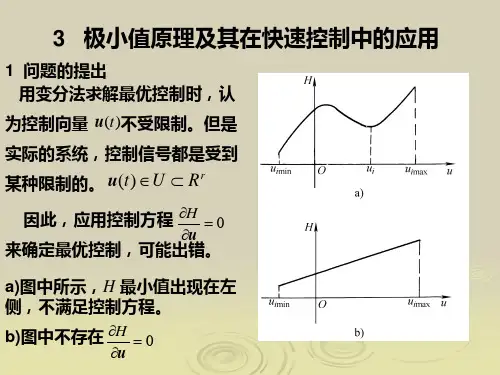
§ 7. 3 极小值原理极小值原理是前苏联数学家庞特里亚金首提. 是变分法的延伸和推广,亦称极大值原理是解决控制和状态受约束最优控制问题的有力工具. 极小值原理的一种表述及其应用(不证) 1. 极小值原理 定理7.3 设==00()[(),(),],()xt f x t u t t x t x ， 指标=+⎰0[(),(),]d [()]Tt J F x t u t t t S x T ，约束∈()()u t U 容许控制集，Hamilton 函数=+(,,,)[,,][,,]TH x u λt F x u t λf x u t ，则*()u t 是最优控制的必要条件是:*()u t 和相应的*()x t , *()λt 满足系统方程，∂=∂H x λ； (7.16)伴随方程，∂=-∂H λx； (7.17) 极值条件，******≤∈[,,,][,,,],,H x u λt H x u λt u u U ；(7.18)边界条件，∂=∂()()x T SλT x 。

(7.19)对(7.12)~(7.15’)，改变的只是极值条件和边界条件。

说明：1) 只有*()u t 才能使Hamilton 函数为全局最小(故名)若无控制约束, 则有∂∂=/0H u .2)边值条件自然含=00()x t x →确定状态和伴随向量. 3)非充要条件。

对线性系统，条件是充要的。

4)解题步骤类似§2中用变分法<1> 作Hamilton 函数→极值条件→待定u (t )； <2> 若伴随方程中无x ，则求出λ；<3>若待定最优控制中不含x →即已求得()u t ；(否则就要解规范方程组)，<4>求出,x J **(若要计算)。

2. 自由终端状态的最优控制举例例 7.5 求状态方程为==,(0)1xu x ， 指标为=⎰1min ()d J x t t ，控制约束为()[1,1]u t ∈-，的最优控制。

离散系统的极小值原理

离散系统的极小值原理
k =0 N −1
（3-4）
当不考虑式（3-1）所示的等式约束时，为了求得上 述离散拉格朗日问题的极值解，对式（3-4）取离散 一次变分：
T T ∂L T ∂Lk ∂Lk k δ J = ∑ δ x( k ) + δ u (k ) + δ x(k + 1) k = 0 ∂x ( k ) ∂u (k ) ∂x(k + 1) N −1
2 离散极小值原理
庞特里亚金发表极小值原理时，只讨论了连续系 统的情况。为了获得离散系统的极小值原理，有 人曾经从离散系统与连续系统比较接近这一事实 出发，设想把连续极小值原理直接推广到离散系 统中去，但除了采样周期足够小的情况外，结果 是失败的。 离散极小值原理的普遍论述比较复杂，证明过程 也十分冗长。为了简单起见，下面介绍控制向量 序列不受约束情况下的离散极小值原理，然后不 加证明地推广到控制向量序列受约束的情况。
当控制序列不受约束时，可以采用离散变分法求 解离散系统的最优控制问题，得到离散极值的必 要条件——离散欧拉方程。 设描述离散系统的状态差分方程为：
x(k + 1) = f [ x(k ), u (k ), k ]
（3-1）
式中 x(k ) 是离散时刻 tk 的 n 维状态；u (k ) 是 tk 的 m f 维控制向量； (•)是 n 维向量函数序列，对于等间 N 隔采样， = kT ， 为采样周期； 为数据窗口长度。 T k
目录
离散欧拉公式 离散极小值原理
随着数字计算机日益普及，计算机控制系统日 益增多，因此，离散系统最优控制问题的研究 显的十分重要，其原因是，一方面许多实际问 题本身就是离散的，另一方面，即时实际系统 是连续的，但为了对连续系统采用计算机控制， 需要把时间整量化，从而得到一离散化系统。

大学课件《微积分》极小值原理

大学课件《微积分》极小值原理

§7－1 极小值原理
例. 给定受控系统：
x1 x1 u
x1(0) 1
x2 x1
x2(0) 0
控制变量 u 满足如下不等式
1 u 1
求最优控制和最优轨迹，使如下性能指标取得极小值。
J x1(1) 解：哈密尔顿函数为H L(x,u,t) T f (x,u,t)
协状态方程：




H x
1 2
(g )T x
x1x1


u


1(x1
* *
1
1
* 0
u) 2 *2
x1
§7－1 极小值原理
运用极小值原理：H[x*,u*, *] min H[x*,u, *]
u 1
min {1*(u x1*) *2x1*}
最优轨迹x*(t) 为下述状态方程的解：
x*(t) Ax*(t) Bu *(t)， x*(0) x0
而最优性能值为：J *

1 2
x0T
P(0)x0，
x0

0
第八章 线性二次型最优控制问题
其中， P(t) 为下述黎卡提微分方程的半正定对称解阵：
P(t) P(t)A AT P(t) Q P(t)BR 1BT P(t) P(t f ) S，t [0, t f ]
有限时间问题与无限时间问题，对控制及控制系统的要求有着显著 的不同；而跟踪问题则可以看作是调节问题的一种推广。
二. 有限时间LQ调节问题
1．结论：对于有限时间LQ调节问题u*，(t) 为具有最优控制的充要
条件是其具有如下形式：
u*(t) K *(t)x*(t)， K *(t) R1BT P(t)

极小值原理

极小值原理
解：为简单计，取 2。问题是要确定最优控 u * (0), u * (1); N 制 最优轨迹x* (1)，x* (2)及最优性能泛函 * 2 [ x(0)],先考虑最后一 J 步，即由状态 (1)，转移到x(2)这一步。如果采用控制 (1),则有 x u 1 2 1 2 1 2 1 x(2) x(1) u (1), J1[ x(1)] u (1) Cx (2) u (1) c[ x(1) u (1)]2 2 2 2 2 最优控制u (1)应使由状态x(1)出发时J1[ x(1)]为最小，故有 J1[ x(1)] u (1) c[ x(1) u (1)] 0 u (1) cx(1) * c x(1) * x(1) 因此得u * (1) , J 1[ x(1)] , x (2) 1 c 2 1 c 1 c 实际上，它们都是这一 段初始状态x(1)的函数。
综上可得： c 最优控制为u (0) x ( 0) 1 2c c c * u (1) x(1) x(0) 1 c 1 2c 最优轨迹为x* (0) x0
*ห้องสมุดไป่ตู้
1 c x (1) x(0) 1 2c 1 1 x* (2) x(1) x(0) 1 c 1 2c
2）求 (t )以确定u的切换点 H 由协态方程 (1 )得＋＝－ ，其解为＝－ ＋Ce t 1 1 x 当t f 1时 (t f ) (1) 0, C e, 故切换点：令 1, 得t 1 ln 2 0.307
二、补充说明
1、式H [ x* (t ), u * (t ), * (t ), t ] H [ x* (t ), u (t ), * (t ), t ] 说明当u (t )和u (t )都从容许的有界集中取 值时，

动态规划与极小值原理

动态规划与极小值原理
来求解。我们可看出 n 阶段与 n 1 阶段有下面的
关系（ n 1, 2, N ）
Tn
x

mintx,
un ( x)
un
(x)

Tn1 un
(x)
（6-1）
T1x t1(x, E)
（表示最后一级）
n 1,2 N
(6-1)式称为函数方程，从(6-1)式可见,在选择了决

min24

6 4

6
最优决策 u3 (B1 ) C2
从B2到E有两种路线：B2C2E 和 B2C3E 。 最短时间为
T3
(B2
)

min
C2 ,C3
tt((BB22
, C3 ,C2
) )

T2 T2
(C3 (C2
) )

7 min6

5 4

动态规划是贝尔曼(Bellman)在五十年代为解决 多级决策过程而提出来的。它可以解决很多领域中 的问题，如生产过程的决策，收益和投资问题，有 多级反应器的化工装置的设计，多级轧钢机的最速 轧制问题，资源分配、机器负荷分配、生产计划编 制，特别是控制工程问题。
它和极小值原理一样，可解决控制变量受约束
显然当段数很多时，计算量是很大的。这种 方法的特点是从起点站往前进行，而且把这四级
决策一起考虑。应注意从到 A 下一站 B2 所花的
时间为1，而到 B1 所花时间为3，但最优路线却 不经过 B2 。
这说明只看下一步的“眼前利益”来作决策 是没有意义的。
（二）动态规划法
为将问题表达得清楚，引进下面的术语。
令 n 表示由某点 E 到终点的段数（如 C2 到 E 为2

极小值原理及其应用

极小值原理及其应用

于是，通过不等式放缩，式（2-6）变为：
x(t ) e bl
at f
x (t ) 与 0 是同阶小量。 上式表明 由式（2-4）知，当取如上变分 u(t ) 时， 性能泛函增量可表示为：
J

l


f [ x (s),u (s)
( )


设下列线性方程：
x (t ) ( x(t ) )
f ( x, u ) x x T x
（2-3）
的状态转移矩阵为 (t , s) ，考虑到 x(t0 ) 0 将方程（2-3）的解带入式(2-1)可得
J

[ x (t f )] x (t f )
H[ x (s), (s),u (s)


u(s)]
H[ x (s), (s),u (s)]ds ( )
（2-9）
（4）极小值条件的推证 因为已设 u (t )、x (t ) 为最优解，故式（2-9） 满足： （2-10） J 0

由 x (t )、 (t )、u (t )、u (t ) 在积分范围内连 续，故H是连续的。根据积分中值定理有
当 t f 自由时
H[ x (t ),u (t ), (t )] 0
f f f
极小值原理与经典变分法相比：控制输入 受约束；最优控制使哈密顿函数取全局极 小值；极小值原理不要求哈密顿函数对控 制的可微性。
2.2极小值原理的证明
证明思路：采用扰动法，即给最优控制一 个变分 u ，它将引起最优轨线的变分 x 并使性能指标有一增量 J ，当J为极小 时，必有 J 0 ，由此即可导出最优控 制所应满足的必要条件。 在证明过程中，需要采用如下引理： d 引理1：

极小值原理及应用_2023年学习资料

极小值原理及应用_2023年学习资料

定理3-2（积分型最优控制问题的极大值原理-给定系统的状态方程-Xt=f[xt,Ut,t]-初态-Xto= o2-终端时刻t固定，终端状态Xt自由以及控制变量U所受约-束条件是-Ut∈2，It∈[ttr]-则为将系 从给定的初态X转移到某个终态Xt，并使性-能泛函-J=∫L[X,U,小d-达到极小值的最优控制应满足的必要 件是：-10
说明：-1当控制函数U不受约束或只受开集性约束条件下，-OH-等价-aU-H[X*t,2t,Ut,t]=m nH[X*t,t,Ut,t]-ut-2在控制函数Ut受到闭集性约束Ut∈2CRm的条件下，控-制方程-H= 未必是最优控制问题的解的必要条件之一。-6x{-观1a-x-b.Hamilton函数H[X,2t,Ut,t 在闭子集2内可能-不存在极值点，以∂H/aU来求极小值点难以奏效。-结论：-6H-控制方程-=01-不是问 3-1所给定的最优控制问题解的-必要条件。
1设产是最优控制，X*t是对应于U*t的最优轨线，则必存-在一与U产和X*t相对应的n维协态变量t,使得X 和2t-满足规范方程：-aH-●-X=-=f[Xt,Ut,t]-0λ -0=--OX-H:哈密顿函数-H=H Xt,t,Ut,t]=-L[Xt,Ut,t]+'tfLXt,Ut,t]-2边界条件为-Xt=X。-2t=0 3哈密顿函数在最优控制U*和最优轨线X*上达到最大值，即-他层-H[X"t,t,U"t,t]=max H[ "t,At,Ut,t]-Ut2-11
如果不考虑约束条件-Ut∈Ω CRm-1,那么该最优控制-问题的解的必要条件可由定理2-10给出，现引述如下 -1设U*t是最优控制，X*是对应于U*t的最优轨线，则-必存在一与U*t和X*t相对应的n维协态变量2t 使得Xt与-λ t满足规范方程-OH-控制函数U不受约束-X=-=f[Xt,Ut,t]-02-或只受并集性的 束的-t=-情况下的最值原理-OX-其中-H=L[Xt,Ut,t]+2tf[Xt,Ut,t]-2边界条件为 X to=Xo-t=0-3哈密顿函数H对控制变量Utto≤t取极值，即-9是=0=→-H[X,20,U'0 ]=min H[X0,20,U0,15

极小值原理及其应用

极小值原理及其应用
线 x* (t) ，必存在非零的 n 维向量函数 (t)，使得
① x(t) 及 (t)满足下述正则方程：
x(t) H
（5-1）
(t) H
x
式中哈密顿函数
（5-2）
H (x,u, ) T (t) f (x,u) （5-3）
② x(t) 及 (t)满足边界条件：
x(t0 ) x0
(t
f
)
（5-73）
因此，定理5-2中凡包含 及其导数的地方，都要
以
~
相应地替代，从而有
~
(t
f
)
[ x(t
x(t f
f )] )
[ x(t
x(t f
f )] )
T [x(t f
x(t f )
)]
（5-74）
以及
H[x* (t f * ), (t f * ), u* (t f ), t f * ]
2 (t) c2
式中 c1 和 c2为待定常数
由横截条件（5- 4）得
1(t f
)
t f 1
x1 (1)
0
2 (t f
)
t f 1
x2 (1)
1
解出 c1 e1, c2 1 ，故有
1(t) 1 et1
由极小值条件（5-13），得
u*(t) sgn{1(t)} 不难发现：1(0) 1 e1 0, 1(1) 0
x为* (为t) 为相应的最优轨线，则必存在非零常向量 及 n 维向量函数 (t) ，使得 x*(t), u*(t), t f * 和 (t) 满足如下必要条件：
① x(t) 及 (t)满足下述正则方程：
x(t) H
式中哈密顿函数
(t) H

极小值原理的证明与探析

极小值原理的证明与探析

( 1) 标量函数 U, 向量函数 f 均为各自宗量 x, u, t 的连续函数, 且 5U/ 5x, 5U/ 5t , 5f / 5x, 5f / 5t
存在, 是 x, t 的连续函数。H是 x( tf ) 的可微函数。
( 2) f [ x, u, t] 在 x 的零点对 x 满足一致( 大) 李卜希茨( L ipschit z) 条件, 即v M > 0, L > 0
$
5H 5x
C
5H
[ x* , K, u, 5x
t]
-
5H * ( t) 5x
式( 10) 化简为
∫ $ J 1( u) =
tf t0
$
5H 5x
T
Dx +
$ H ( t)
dt +
0( ‖Dx‖M )
( 11)
1. 2. 5 求证式( 3)
证明: 因为 u* ( t) 是最优控制, 所以
$J 1( u) ≥0 P u∈8
8 C u( t) ∶u( t ) ∈ R r ∩ t ∈ [ t0, tf ] ∩ 分段连续向量 ∩ g[ u( t) , t ] ≥ 0 ( 4)
所谓分段连续向量, 是指除在有限个间断点半连续[ u( t) = u( t - ) 或 u( t + ) ] 以外, 处处连续
的函数向量。
收稿日期: 1997- 08- 30 高越农, 男, 1936 年生, 教授; 武汉, 武汉冶金科技大学工业自动化系( 430081) 。
H ～( t1 ) C H [ x* ( t1 ) , K( t1 ) , u* ( td + ) , t 1]
H ～( t d- ) = H [ x* ( t d- ) , K( td- ) , u* ( td + ) , td- ] = H * ( td+ )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t f t 0

(8-16)
下面求泛函 J a 的变分。这里，假设终端时刻 t f 及终端状态 x t f 均自由。经过同变分法中的类似推导，最后得
x t f ， t f t Ja f x t f
x t f
第八章 极小值原理
在用古典变分法求解最优控制问题时，假定控制变量 u t 不受任 何限制，即容许控制集合可以看成整个m维控制空间开集，这 时控制变分 δ u 可以任取。同时还严格要求哈密尔顿函数H对u连
续可微。在这种情况下，应用变分法求解最优控制问题是行之
有效的。
但是，实际工程问题中，控制变量往往是受到一定限制，
f J x t ， t F x t ， u t ， t d t f f t 0

t
(8-9)
为极小。 设对应于最优情况的性能指标为 J u * ，仅考虑由于 u * t 偏离 u t 时的性能指标为 J u ，则按最优的定义，下式必然成立
t f t 0

(8-3)
* * 则使性能指标 J 达到极小的最优控制 u t 及最优状态轨线 x t 必须满足以下条件：
⑴ 正则方程
x* t H
H
(8-4)
a
* t
(8-5)
a
H 为哈密尔顿函数， 为协态变量，其定义与在变分法中 这里， 相同。
T

x t f ， t f H x t ， u t ， t ， t f f f f t f t f
tf t0 T T H x， u ， λ ， t H x， u ， λ ， t x u x u
当u t 受边界限制时，泛函极小的必要条件是：
Ja 0
(8-24)
为了寻找 u 与 J a 的关系，在式(8-16)中可令除含有 u 项以 外的各项均为零，则泛函极小必要条件式(8-23)变成
* * * H x ， u ， λ ， t t f * J u ， u u d t 0 a t 0 u T
我们对式(8-27)作一些简单解释，假定控制变分 u 出现在 t 0， t f * 区间的某一小区 t1，t 2 内，而在其它区间内部为最优控制 u t * * * * * x ， u ， λ ， t H x ， u ， λ ， t 则如果式(8-27)不满足，即存在 H ， 指标泛函变分式可表示成：
Ju Ju J 0 *
设 u * t 偏离 u t 足够小
* u t ut u t
(8-10)
则由此引起的的增量可以由下式表示
* * * J u ， u J u ， u u ， u

⑵ 哈密尔顿函数对应最优控制时为极小值，即：
* m i n H x * t ， ut ， ， t t uU
H x * ， ut ， t ， t t
*
(8-5)
或
* * H x * t ， u t ， t ， t H x * t ， u t ， t ， t (8-6) u U
优控制问题的有力工具。它是由苏联学者庞特里亚金于1956 年提出的。极小值原理从变分法引伸而来，它的结论与古典变 分法的结论极为相似，但由于它能应用于控制变量 u t 受边界 限制的情况，并不要求哈密尔顿函数H对u连续可微，因此其
适用范围扩大了。
L.S.Pontryagin
第一节 连续系统的极小值原理

(8-11)
* * Ju ， u 这里， u ， u 表示二阶及二阶以上的高阶项， 是 J 的 * ， u 0 u 线性主部，它与 u 成线性关系。当 u 0 时 这时 * u ， u 来近似代替泛函的实际增量 Ju， 可以由泛函变分 Ju
T
(8-26)
* H ， u u
代入式(8-24)，得：
J u ， u xu ， u ， λ ， t － H xu ， ， λ ， t d t (8-27) H
* t f * * * T * * * a t 0
0
(8-17)
T H x， u ， λ ， t x λ dt λ
根据泛函存在极值的必要条件的结论可知，当 u t 不受限制时， 应满足 (8-18) Ja 0
由于各个变量的变分是独立的，因此，必须同时满足
* * * H x ，，， u λ t * λ 0 x
(8-30)
到此，极小值原理得证。 极小值原理同时还给出以下条件，即：如果哈密尔顿函数不 显含变量 t ，则哈密尔顿函数 H 沿最优轨线保持为常数，即
* * * H xu t ， t ， λ t ， t c t t ， t (8-31) 0 f

t



(8-14)
定义哈密尔顿函数
T H x ， u ， ， t F x ， u ， t f x ， u ， t (8-15)



则得
J x t t H x ， u ， ， t x d t a f， f
ut u t u 均处在容许集内，这种情况下，泛函达极小值 取， 的必要条件为：
*
* J u ， u 0
(8-12)
图8-1 u t 的容许域
u * t 处在容许集的边界上， u 不能任取，它 ⑵ 在 t1，t 2 区间内， 只能取负值，这时泛函为极小值的必要条件应为：
* x t t f， f * * * H x t ，，， u t λ t t 0 f f f f t f
这里，式(8-19)、式(8-20)为正则方程，式(8-21)为控制方程， 式(8-22)，式(8-23)为横截条件，这与第六章变分法中所得结论 完全相同。
* * * H x ，，， u λ t * x 0 λ
ቤተ መጻሕፍቲ ባይዱ
(8-19) (8-20) (8-21) (8-22) (8-23)
* * * H x ， u ，， λ t
u
0
* x ， tf tf * tf 0 x t f
* * * * * * Ja u ， u H x ， u ， λ ， t H x ， u ， λ ， t dt * t0 * * * * * * H x ， u ， λ ， t H x ， u ， λ ， t dt t2 t1 t1
显然，这与 J a 0 矛盾。同时，小区间t1，t 2 可能出现在 t ， t 区间的任何位置，因此要求整个区间 t ， t 内均满足以下条 件
0 0 f
f

* * * * * H x ， u ， λ ， t H x ， u ， λ ， t
x t f x t，， u t t
(8-7)
x t0 x0，为简单起见，假设终端时刻 t f 及终端 边界条件为： 状态 x t f 均为自由。控制变量 u t 受有界闭集约束，即
u t U
(8-8)
* 求最优控制 u t 使性能指标


当不受边界限制时，则上式与等效。
⑶ 根据不同的边界情况，x * t 及 * t 满足相应的边界条件及 横截条件，它们与变分法中所应满足的边界条件及横截条 件完全相同。
比较上述极小值原理与变分法所得的结果，可以发现两者的差 别仅在⑵。 极小值原理的严格证明很复杂，下面的证明将重于物理概念的 阐述，尽量避免烦琐的数学推导。 设系统动态方程为：
* J u ， u 0
(8-13)
这说明对 u * t 的任何容许偏离都会引起泛函 J u * 比其足够小 u 要小，故有可能为极小。 的邻区内的值J u*， 下面，根据以上结论来求泛函极小的具体条件。首先，用拉格 朗日乘子法建立增广泛函
f T J x t ， t F x ， u ， t f x ， u ， t x d t a f f t 0
设连续系统动态方程为：
x t fx t，， u t t
(8-1)
边界条件可以固定、自由或受轨线约束，控制变量 u t 属于m维 有界闭集U，即
m ut U R
(8-2)
性能指标为：
J x t t F x t ， u t ， t d t f， f
以上条件应对 t t0，t f 出现的容许 u 都满足，由此可得以下 结论：使指标泛函达极小的最优控制的必要条件是：
* * * * * (8-28) H x t ， u t ， λ t ， t H x t ， u t ， λ t ， t
H u， λ， t u， λ， t x ， H x ， dt t1
* * * * * * * * * * dt H x ， u ， λ ， t H x ， u ， λ ， t t1 t2
t2
(8-29)
0
(8-25)
这里，被积函数为哈密尔顿函数对于控制变分引起的增量的线 性主部。当 u 足够小时，可用它来一次近似代替实际增量，即