随机一致性指标求解

高校学院思想政治教育评估模型分析：大学生思想政治教育越来越受到广泛关注，对于当今社会，独生子女的心里影响，一直是社会头疼的问题，而独生子女占了大学生的大部分，如何能够引导大学生积极乐观进取的生活态度，一直是教育的关键因素。

如果教育出来的学生大多是心里有问题的，那么说明我们的教育是失败的。

教育者如何去做呢？那得有依据，所以我们针对我们学校的思想政治教育情况，做了本次调查，并作出了相应的模型。

由于我校属于边远的民族学校，所以它将适宜这类学校的学生思想政治教育情况。

我们采用层次分析的方法，首先发出问卷调查，再对问卷提取信息，进行数据分析，建立相应的模型。

我们对问卷内容采取两两比较的方式，主要情况有：两者同等重要，两者相比稍微重要、明显重要、强烈重要和绝对重要。

而所用的数值分别为1 ，3,5,7,9,1/3,1/5,1/7,1/9.如果认为两者相比后，在以上各数据之间，则用2,4,6,8,1/2,1/4,1/6,1/8，具体情况详见后面的附表。

我们本次共发出问卷120份，共收回110份，回收率为91.76%，其中教师发出20份，回收10份，回收率为50%；针对全院学生发出100份，回收100份，回收率为100%。

符号说明：A表示一级指标矩阵；1a表示工作理念与工作理念相比较；11a表示工作理念与队伍建设相比较12a表示工作理念与教育管理相比较；13a表示工作理念与咨询服务相比较；14a表示工作理念与工作效果相比较；15a表示队伍建设与教育管理相比较；231224a 表示队伍建设与咨询服务相比较； 25a 表示队伍建设与工作效果相比较； 34a 表示教育管理与咨询服务相比较； 35a 表示教育管理与工作效果相比较； 45a 表示咨询服务与工作效果相比较；21a ，22a ，31a ，32a ，33a ，43a ，54a ，53a 分别与上面相反。

1B 表示二级指标中在工作理念下的矩阵； 12b 表示工作定位与工作思路相比较； 21b 表示工作思路相与工作定位比较；1C 表示二级指标中在队伍建设下的矩阵； 12c 表示专职干部队伍与专业导师队伍相比较； 13c 表示专职干部队伍与学生骨干队伍相比较；23c 表示专业导师队伍与学生骨干队伍相比较； ii c 表示自身与自身相比较； 21c ，31c ，32c 分别与上面相反。

层次分析法1层次分析法首先建立了层次结构模型后，其上下层之间元素的隶属关系就被确定了。

最后需要对每一个层级的所有指标进行两两对比，确定其相对的重要性。

而层次分析通常采用Saaty 标度法来给判断矩阵的元素赋值。

如表1-1所示：表1-1 1~9标度及其含义模糊标度定义 说明1 同等重要 表示两元素相比，同等重要 3 稍微重要 表示两元素相比，前者比后者稍微重要 5 明显重要 表示两元素相对，前者比后者明显重要 7 强烈重要 表示两元素相对，前者比后者强烈重要 9 极端重要表示两元素相对，前者比后者极端重要2、4、6、8表示上述相邻判断的中间值倒数若元素i 和元素j 的重要性之比为ij a ，那么元素j 与元素i 的重要性之比为1/ji ij a a =1.1层次分析法计算步骤依据表1-1我们可以得到要素层与各方案层的两两判断矩阵()ij n nA a ´=，其次通过下列步骤进行权重的计算以及一致性检验。

（1）我们利用方根法求评价因素的权重向量近似值，其计算公式如下：11,(1,2,...,)nni ij j w a i n =⎛⎫== ⎪⎝⎭∏（2）对上述利用方根法求解的权重向量按照下列公式做归一化处理，得到最终的权重为：'1,(1,2,...,)ii nik w w i n w===∑（3）计算判断矩阵的最大特征值m ax λ。

()max 1=nii iAw nw λ=∑（4）一致性检验，由一致性指标：max 1nCI n λ-=-RICI CR =其中，一致性指标CI 越大，这就意味着矩阵的偏离一致性就越大。

反之一致性指标CI 越小，则这就意味着矩阵的偏离一致性就越小。

并且当矩阵的阶数n 越大时，其最大特征值max λ也就会越大，这就可能会导致CI 变得更大，也就意味着矩阵的偏离一致性就越大。

反之，阶数n 越小，最大特征值max λ就会越小，其一致性指标CI 也就越小，则这就意味着矩阵的偏离一致性就越小。

东南大学《数学实验》报告学号姓名成绩实验内容：一实验目的1.掌握matlab基本矩阵编程计算方法2.加深对层次分析法的理解3.掌握矩阵随机一致性指标RI的计算过程二实验思路为了求任意n阶矩阵的随机一致性指标RI的值，我们需要做以下几步工作1.先构造n阶的正互反矩阵2.求正互反矩阵的特征值3.找出最大特征值4.取多个n阶正互反矩阵最大特征值的平均值5.计算相应的RI值三实验内容与要求1.实验代码及说明RI=zeros(1,30); %zeros(m,n)产生m*n的double类零矩阵，zeros(n)产生n*n的全0阵。

%定义了结果输出格式（行向量）for n=3:30 %定义n的范围；3-30times=10000; %任意n阶矩阵产生10000个正互反矩阵enum=[9 8 7 6 5 4 3 2 1 1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9]; %定义一维矩阵enumx=zeros(1,times); %定义最大特征值向量并初始化A=ones(n,n); %先生成n阶幺矩阵，矩阵所有元素都为1for num=1:times %循环for i=1:nfor j=i+1:n %先找到正互反矩阵的上三角A(i,j)=enum(ceil(17*rand(1))); %rand（1）随机生成一个位于区间（0，1）的数%17*rand（1）则随机生成位于区间（0，17）的数，%经ceil函数取整后得到一个1-17之间的整数。

%则A(i，j）的值为矩阵enum中的某一个A(j,i)=1/(A(i,j)); %矩阵的下三角元素是上三角元素的倒数A(i,i)=1; %对角线元素取1%以上五段为构造正互反矩阵endendV=eig(A); %求矩阵的特征值x(num)=max(V); %以最大特征值给x向量赋值endk=sum(x)/times; %最大特征值平均值RI(n)=(k-n)/(n-1); %算出对应RI的值endRI2.实验结果（随机运行两次代码，得到不同的结果）（1）RI =1 至 14 列0 0 0.5258 0.8924 1.1099 1.2507 1.3353 1.40871.4526 1.4876 1.5111 1.5369 1.5550 1.570415 至 28 列1.5834 1.5950 1.6057 1.6159 1.6199 1.6280 1.6355 1.6402 1.6463 1.6508 1.6541 1.6597 1.6633 1.666129 至 30 列1.6700 1.6723（2）RI =1 至 14 列0 0 0.5285 0.8935 1.1077 1.2530 1.3420 1.40261.4539 1.4903 1.5121 1.5346 1.5570 1.571915 至 28 列1.5865 1.5946 1.6055 1.6149 1.6233 1.6292 1.6354 1.6413 1.6462 1.6522 1.6554 1.6593 1.6642 1.666729 至 30 列1.6695 1.67203.结果分析虽然运行两次得到的结果不同，但差距并不是很大，可以大致得到n 阶矩阵对应的RI值的范围。

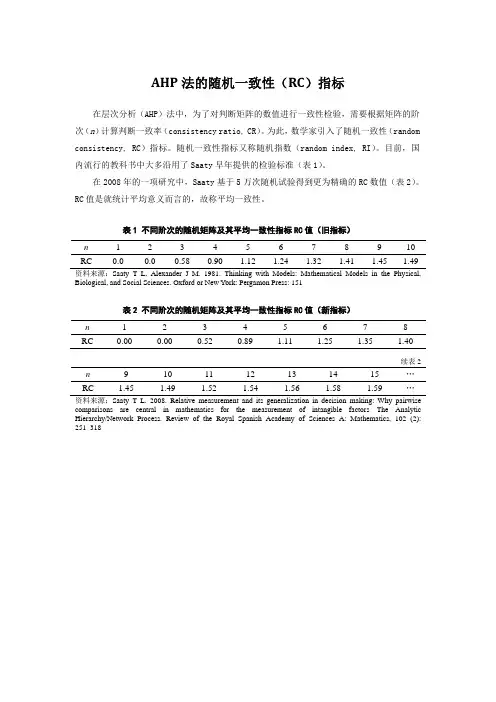
AHP法的随机一致性（RC）指标在层次分析（AHP）法中，为了对判断矩阵的数值进行一致性检验，需要根据矩阵的阶次（n）计算判断一致率（consistency ratio, CR）。

为此，数学家引入了随机一致性（random consistency, RC）指标。

随机一致性指标又称随机指数（random index, RI）。

目前，国内流行的教科书中大多沿用了Saaty早年提供的检验标准（表1）。

在2008年的一项研究中，Saaty基于5万次随机试验得到更为精确的RC数值（表2）。

RC值是就统计平均意义而言的，故称平均一致性。

表1 不同阶次的随机矩阵及其平均一致性指标RC值（旧指标）n 1 2 3 4 5 6 7 8 9 10 RC 0.0 0.0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49资料来源：Saaty T L, Alexander J M. 1981. Thinking with Models: Mathematical Models in the Physical, Biological, and Social Sciences. Oxford or New York: Pergamon Press: 151表2 不同阶次的随机矩阵及其平均一致性指标RC值（新指标）n 1 2 3 4 5 6 7 8 RC 0.00 0.00 0.52 0.89 1.11 1.25 1.35 1.40续表2 n 9 10 11 12 13 14 15 …RC 1.45 1.49 1.52 1.54 1.56 1.58 1.59 …资料来源：Saaty T L. 2008. Relative measurement and its generalization in decision making: Why pairwise comparisons are central in mathematics for the measurement of intangible factors—The Analytic Hierarchy/Network Process. Review of the Royal Spanish Academy of Sciences A: Mathematics, 102 (2):251–318。

权重确定方法归纳多指标综合评价是指人们根据不同的评价目的,选择相应的评价形式据此选择多个因素或指标,并通过一定的评价方法将多个评价因素或指标转化为能反映评价对象总体特征的信息,其中评价指标与权重系数确定将直接影响综合评价的结果;按照权数产生方法的不同多指标综合评价方法可分为主观赋权评价法和客观赋权评价法两大类,其中主观赋权评价法采取定性的方法由专家根据经验进行主观判断而得到权数,然后再对指标进行综合评价,如层次分析法、综合评分法、模糊评价法、指数加权法和功效系数法等;客观赋权评价法则根据指标之间的相关关系或各项指标的变异系数来确定权数进行综合评价,如熵值法、神经网络分析法、TOPSIS法、灰色关联分析法、主成分分析法、变异系数法等;两种赋权方法特点不同,其中主观赋权评价法依据专家经验衡量各指标的相对重要性,有一定的主观随意性,受人为因素的干扰较大,在评价指标较多时难以得到准确的评价;客观赋权评价法综合考虑各指标间的相互关系,根据各指标所提供的初始信息量来确定权数,能够达到评价结果的精确但是当指标较多时,计算量非常大;下面就对当前应用较多的评价方法进行阐述;一、变异系数法一变异系数法简介变异系数法是直接利用各项指标所包含的信息,通过计算得到指标的权重;是一种客观赋权的方法;此方法的基本做法是：在评价指标体系中,指标取值差异越大的指标,也就是越难以实现的指标,这样的指标更能反映被评价单位的差距;例如,在评价各个国家的经济发展状况时,选择人均国民生产总值人均GNP作为评价的标准指标之一,是因为人均GNP不仅能反映各个国家的经济发展水平,还能反映一个国家的现代化程度;如果各个国家的人均GNP没有多大的差别,则这个指标用来衡量现代化程度、经济发展水平就失去了意义;由于评价指标体系中的各项指标的量纲不同,不宜直接比较其差别程度;为了消除各项评价指标的量纲不同的影响,需要用各项指标的变异系数来衡量各项指标取值的差异程度;各项指标的变异系数公式如下：式中：是第项指标的变异系数、也称为标准差系数；是第项指标的标准差；是第项指标的平均数;各项指标的权重为：二案例说明例如,英国社会学家英克尔斯提出了在综合评价一个国家或地区的现代化程度时,其各项指标的权重的确定方法就是采用的变异系数法;案例：利用变异系数法综合评价一个国家现代化程度时的指标体系中的各项指标的权重;数据资料是选取某一年的数据,包括中国在内的中等收入水平以上的近40个国家的10项指标作为评价现代化程度的指标体系,计算这些国家的变异系数,反映出各个国家在这些指标上的差距,并作为确定各项指标权重的依据;其标准差、平均数数据及其计算出的变异系数等见表1-1;i ii x V σ=()n i ,,2,1 =iV i i σi i xi ∑==ni iii VV W 1计算过程如下：1先根据各个国家的指标数据,分别计算这些国家每个指标的平均数和标准差；2根据均值和标准差计算变异系数; 即：这些国家人均GNP 的变异系数为：农业占GDP 比重的变异系数：其他类推;3将各项指标的变异系数加总：4计算构成评价指标体系的这10个指标的权重： 人均GNP 的权重：农业占GDP 比重的权重：其他指标的权重都以此类推; 三变异系数法的优点和缺点当由于评价指标对于评价目标而言比较模糊时,采用变异系数法评价进行评定是比较合适的,适用各个构成要素内部指标权数的确定,在很多实证研究中也多数采用这一方法;缺点在于对指标的具体经济意义重视不够,也会存在一定的误7 966.270.66711 938.4ii iV x σ===782.0352.9316.7===iii x V σ0.6670.7820.2360.560.537 4.59+++++=145.059.4667.01===∑=ni iii VV W 1704.059.4782.01===∑=ni iii VV W差;二、层次分析法一层次分析法概述人们在对社会、经济以及管理领域的问题进行系统分析时,面临的经常是一个由相互关联、相互制约的众多因素构成的复杂系统;层次分析法则为研究这类复杂的系统,提供了一种新的、简洁的、实用的决策方法;层次分析法AHP法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法;该方法将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题;二层次分析法原理层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层供决策的方案、措施等相对于最高层总目标的相对重要权值的确定或相对优劣次序的排定;层次分析法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法;尤其适合于对决策结果难于直接准确计量的场合;三层次分析法的步骤和方法•建立层次结构模型•构造判断（成对比较）矩阵•层次单排序及一致性检验•层次组合排序及一致性检验1. 建立层次结构模型利用层次分析法研究问题时,首先要把与问题有关的各种因素层次化,然后构造出一个树状结构的层次结构模型,称为层次结构图;一般问题的层次结构图分为三层,如图所示;最高层为目标层O ：问题决策的目标或理想结果,只有一个元素;中间层为准则层C ：包括为实现目标所涉及的中间环节各因素,每一因素为一准则,当准则多于9个时可分为若干个子层;最低层为方案层P ：方案层是为实现目标而供选择的各种措施,即为决策方案;一般说来,各层次之间的各因素,有的相关联,有的不一定相关联；各层次的因素个数也未必一定相同．实际中,主要是根据问题的性质和各相关因素的类别来确定;层次分析法所要解决的问题是关于最低层对最高层的相对权重问题,按此相对权重可以对最低层中的各种方案、措施进行排序,从而在不同的方案中作出选择或形成选择方案的原则;2. 构造判断成对比较矩阵构造比较矩阵主要是通过比较同一层次上的各因素对上一层相关因素的影响作用．而不是把所有因素放在一起比较,即将同一层的各因素进行两两对比;比较时采用相对尺度标准度量,尽可能地避免不同性质的因素之间相互比较的困难;同时,要尽量依据实际问题具体情况,减少由于决策人主观因素对结果造成的影响;决策目标o准则1C 1准则2C 2准则m 1C m1子准则1C 11子准则2C 21方案1P 1方案2P 2方案nP n子准则m 2 C m21设要比较n 个因素n C C C ,,,21 对上一层如目标层O 的影响程度,即要确定它在O 中所占的比重;对任意两个因素i C 和j C ,用ij a 表示i C 和j C 对O 的影响程度之比,按1～9的比例标度来度量),,2,1,(n j i a ij =．于是,可得到两两成对比较矩阵n n ij a A ⨯=)(,又称为判断矩阵,显然0>ij a ,),,2,1,(,1,1n j i a a a ii ijji ===因此,又称判断矩阵为正互反矩阵．比例标度的确定：ij a 取1-9的9个等级,ji a 取ij a 的倒数,1-9标度确定如下：ij a = 1,元素i 与元素j 对上一层次因素的重要性相同； ij a = 3,元素i 比元素j 略重要； ij a = 5,元素i 比元素j 重要； ij a = 7, 元素i 比元素j 重要得多； ij a = 9,元素i 比元素j 的极其重要； 2ij a n =,1,2,3,4n =元素i 与j 的重要性介于21ij a n =-与21ij a n =+之间；1ij a n=,1,2,9n =当且仅当ji a n =;由正互反矩阵的性质可知,只要确定A 的上或下三角的2)1(-n n 个元素即可;在特殊情况下,如果判断矩阵A 的元素具有传递性,即满足),,2,1,,(n k j i a a a ij kj ik ==则称A 为一致性矩阵,简称为一致阵． 3. 层次单排序及一致性检验3.1相对权重向量确定 1和积法取判断矩阵n 个列向量归一化后的算术平均值,近似作为权重,即),,2,1(111n i a a n w n j n k kjiji ==∑∑==类似地,也可以对按行求和所得向量作归一化,得到相应的权重向量; 2求根法几何平均法将A 的各列或行向量求几何平均后归一化,可以近似作为权重,即),,2,1(111111n i a a w nj nk nn j kj nij n j i =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=∑∑∏∏====3特征根法设想把一大石头Z 分成n 个小块n c c c ,,,21 ,其重量分别为n w w w ,,,21 ,则将n 块小石头作两两比较,记j i c c ,的相对重量为),,2,1,(n j i w w a jiij ==,于是可得到比较矩阵111122221212n n n n n n w w w w w w w w w w w w A w w w w w w ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦显然,A 为一致性正互反矩阵,记12(,,,)T n W w w w =,即为权重向量．且12111,,,n A W w w w ⎛⎫=⋅ ⎪⎝⎭则12111,,,n A W W W nW w w w ⎛⎫⋅=⋅= ⎪⎝⎭这表明W 为矩阵A 的特征向量,且n 为特征根．事实上：对于一般的判断矩阵A 有max A W W λ⋅=,这里)(max n =λ是A 的最大特征根,W 为m ax λ对应的特征向量．将W 作归一化后可近似地作为A 的权重向量,这种方法称为特征根法; 注：现有软件求得最大特征根与特征向量; 3.2一致性检验通常情况下,由实际得到的判断矩阵不一定是一致的,即不一定满足传递性和一致性．实际中,也不必要求一致性绝对成立,但要求大体上是一致的,即不一致的程度应在容许的范围内．主要考查以下指标： 1一致性指标：1max --=n n CI λ．2随机一致性指标：RI ,通常由实际经验给定的,如表2-1;表2-1 随机一致性指标3一致性比率指标：RICI CR =,当10.0<CR 时,认为判断矩阵的一致性是可以接受的,则m ax λ对应的特征向量可以作为排序的权重向量;此时()1max 111nij jnnj ii i iia wA W nw n w λ===⋅≈=∑∑∑其中(A )i W ⋅表示A W ⋅的第i 个分量; 4.计算组合权重和组合一致性检验 1组合权重向量设第1-k 层上1-k n 个元素对总目标最高层的排序权重向量为()1(1)(1)(1)(1)12,,,k Tk k k k n Wwww-----=第k 层上k n 个元素对上一层1-k 层上第j 个元素的权重向量为()(1)()()()121,,,,1,2,,k Tk k k k jj jn jk P p p pj n --==则矩阵1()()()()12,P ,,P k k k k k n P P -⎡⎤=⎣⎦是1-⨯k k n n 阶矩阵,表示第k 层上的元素对第1-k 层各元素的排序权向量．那么第k 层上的元素对目标层最高层总排序权重向量为()1()()(1)()()()(1)12()()()12,P ,,P ,,,k kk k k k k k k n Tk k k n W P W P W w w w---⎡⎤=⋅=⋅⎣⎦=或k k j n j k ij k in i w p wk ,,2,1,)1(1)()(1==-=∑- 对任意的2>k 有一般公式()()(1)(3)(2)(2)k k k W P P P W k -=⋅⋅⋅⋅>其中(2)W 是第二层上各元素对目标层的总排序向量． 2组合一致性指标设k 层的一致性指标为)()(2)(11,,,k nk k k CI CI CI - ,随机一致性指标为 )()(2)(11,,,k n k k k RI RI RI - 则第k 层对目标层的最高层的组合一致性指标为()1()()()()(1)12,,,k k k k k k n CI CI CI CI W --=⋅ 组合随机一致性指标为()1()()()()(1)12,,,k k k k k k n RI RI RI RI W --=⋅ 组合一致性比率指标为)3()()()1()(≥+=-k RICI CRCRk k k k 当10.0)(<k CR 时,则认为整个层次的比较判断矩阵通过一致性检验．四案例说明实例：人们在日常生活中经常会碰到多目标决策问题,例如假期某人想要出去旅游,现有三个目的地方案：风光绮丽的杭州1P 、迷人的北戴河2P 和山水甲天下的桂林3P ;假如选择的标准和依据行动方案准则有5个景色,费用,饮食,居住和旅途;1.建立层次结构模型目标层 准则层2.构造判断矩阵1234511/2433217551/41/711/21/31/31/52111/31/5311C C A C C C ⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪⎝⎭构造所有相对于不同准则的方案层判断矩阵 1相对于景色O 择旅游地P1桂林C1景色C2费用C3居住C4饮食C5旅途P2黄山P3北戴河12345C C C C C 11231251/2121/51/2`1P B P P ⎛⎫ ⎪= ⎪⎪⎝⎭123P P P2相对于费用3相对于居住4相对于饮食5相对于旅途3. 层次单排序及一致性检验3.1用matlab 求得判断矩阵A 的最大特征根与特征向量：max 5.073λ=,对应于max 5.073λ=的正规化的特征向量为：(2)(0.263,0.475,0.055,0.099,0.110)T W =判断矩阵1B 的最大特征值与特征向量max 3.005λ=(3)10.5950.2770.129W ⎛⎫ ⎪= ⎪ ⎪⎝⎭122311/31/8311/383`1P B P P ⎛⎫ ⎪= ⎪⎪⎝⎭123P P P 132********/31/3`1P B P P ⎛⎫ ⎪= ⎪⎪⎝⎭123P P P 14231341/3111/41`1P B P P ⎛⎫ ⎪= ⎪⎪⎝⎭123P P P 1523111/4111/4441P B P P ⎛⎫ ⎪= ⎪⎪⎝⎭123P P P判断矩阵2B 的最大特征值与特征向量max 3.002λ=(3)20.2360.682W ⎪= ⎪ ⎪⎝⎭判断矩阵3B 的最大特征值与特征向量max 3λ=(3)30.4290.429,0.142W ⎛⎫ ⎪= ⎪ ⎪⎝⎭判断矩阵4B 的最大特征值与特征向量max 3.009λ=(3)40.6330.193,0.175W ⎛⎫⎪= ⎪ ⎪⎝⎭判断矩阵5B 的最大特征值与特征向量max 3λ=(3)50.1660.166.0.668W ⎛⎫ ⎪= ⎪ ⎪⎝⎭4.一致性检验对于判断矩阵A 进行一致性检验：max 5.07350.01825151nCI n λ--===--查表知平均随机一致性指标RI,从而可检验矩阵一致性：0.018250.0162950.11.12CI CR RI ===< 同理,对于第二层次的景色、费用、居住、饮食、旅途五个判断矩阵的一致性检验均通过;利用层次结构图绘出从目标层到方案层的计算结果：5.层次总排序各个方案优先程度的排序向量为：(3)(2)W W W =0.5950.0820.4290.6330.1660.3000.4750.2770.2360.4290.1930.1660.2460.0550.1290.6820.1420.1750.6680.4560.0990.110 ⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭决策结果是首选旅游地为3P 其次为1P ,最后为2P ; 五优点与缺点人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统;层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法;在应用层次分析法研究问题时,遇到的主要困难有两个： i 如何根据实际情况抽象出较为贴切的层次结构；ii 如何将某些定性的量作比较接近实际定量化处理;层次分析法对人们的思维过程进行了加工整理,提出了一套系统分析问题的方法,为科学管理和决策提供了较有说服力的依据;但层次分析法也有其局限性,主要表现在：i 它在很大程度上依赖于人们的经验,主观因素的影响很大,它至多只能排除思维过程中的严重非一致性,却无法排除决策者个人可能存在的严重片面性;ii 当指标量过多时,对于数据的统计量过大,此时的权重难以确定;AHP 至多只能算是一种半定量或定性与定量结合的方法;三、熵值法一熵值法的原理在信息论中,熵是对不确定性的一种度量;信息量越大,不确定性就越小,熵也就越小；信息量越小,不确定性越大,熵也越大;根据熵的特性,我们可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响越大; 二算法实现过程 1.数据矩阵m n nm n m X X X X A ⨯⎪⎪⎪⎭⎫ ⎝⎛=1111其中ij X 为第i 个方案第j 个指标的数值; 2. 数据的非负数化处理由于熵值法计算采用的是各个方案某一指标占同一指标值总和的比值,因此不存在量纲的影响,不需要进行标准化处理,若数据中有负数,就需要对数据进行非负化处理;此外,为了避免求熵值时对数的无意义,需要进行数据平移：对于越大越好的指标：mj n i X X X X X X X X X X X nj j j nj j j nj j j ij ij ,,2,1;,,2,1,1),,,min(),,,max(),,,min(212121' ==+--=对于越小越好的指标：mj n i X X X X X X X X X X X nj j j nj j j ijnj j j ij,,2,1;,,2,1,1),,,min(),,,max(),,,max(212121' ==+--=为了方便起见,仍记非负化处理后的数据为ij X 3.计算第j 项指标下第i 个方案占该指标的比重),2,1(1m j XX P ni ijijij ==∑=4.计算第j 项指标的熵值1e 0,ln 10ln ,0,)log(*1≤≤=≥>-=∑=则一般令有关，与样本数。

$ #!$9"#!*’):"#&!%(9"#$!$"! $ #!!9"#!*’):"#!!)"9"#"(&*’ $ #!%9"#!*’):"#!!)"9"#"(&*’ $ #!&9"#!*’):"#$!!&9"#"%&+) $ #%$9"#$&!+:"#(%)"9"#"+$"% $ #%!9"#$&!+:"#$"&)9"#"$&+( $ #%%9"#$&!+:"#!’*%9"#"%(+!
求得 !7389’#" ， /,9" ； 对于 "! 有：
.! /!$ /!! /!% /!& /!$ $ "#’ "#’ $1% /!! ! $ $ "#’ /!% ! $ $ "#’ /!& % ! ! $ 0 "#&!%( "#!!)" "#!!)" "#$!!&
求得 !7389&#"$"% ， /,9"#""%+ ； 对于 "% 有：
#%!、 #%%。
%
判断矩阵
在 6;< 解题手续中， 判断矩阵的构造及其相关的计算， 是
6;< 问题求解的关键 =+>。

1. 层次分析法（The analytic hierarchy process, 简称AHP）用于解决评价类问题,例如：选择那种方案最好、哪位运动员或者员工表现的更优秀。

评价类问题可以用打分解决。

层次分析法 (The Analytic Hierarchy Process即 AHP)是由美国运筹学家、匹兹堡大学教授T. L. Saaty于20世纪70年代创立的一种系统分析与决策的综合评价方法, 是在充分研究了人类思维过程的基础上提出来的, 它较合理地解决了定性问题定量化的处理过程。

AHP的主要特点是通过建立递阶层次结构, 把人类的判断转化到若干因素两两之间重要度的比较上, 从而把难于量化的定性判断转化为可操作的重要度的比较上面。

在许多情况下, 决策者可以直接使用AHP进行决策, 极大地提高了决策的有效性、可靠性和可行性, 但其本质是一种思维方式, 它把复杂问题分解成多个组成因素, 又将这些因素按支配关系分别形成递阶层次结构, 通过两两比较的方法确定决策方案相对重要度的总排序。

整个过程体现了人类决策思维的基本特征，即分解、判断、综合，克服了其他方法回避决策者主观判断的缺点。

1.1模型介绍1.1.1引例高考结束了，小明该选择华科还是五武大？小明最关心四个方面：学习氛围0.4、就业前景0.3、男女比例0.2、校园景色0.19（权重和为1）（1）学习氛围：经查阅资料查到“学在华工，玩在武大，爱在华师”一句话，因此在学习氛围方面给华科0.7，给武汉大学0.3.（2）就业前景：搜索两所学校就业率差不多，因此在就业前景方面对两所学校均赋予0.5的权重。

（3）男女比例：经查询，华科男女比例2：1，武大1.35：1，因此武大0.7分，华科0.3分（4）校园景色：华科0.25分，武大0.75分整理权重表格：指标权重华科武大学习氛围0.40.70.3就业前景0.30.50.5男女比例0.20.30.7校园景色0.10.250.75华科最终的得分：0.7*0.4+0.5*0.3+0.3*0.2+0.25+*0.1=0.515分武大最终得分：0.3*0.4+0.5*0.3+0.7*0.2+0.75*0.1=0.485分1.1.2 模型1、关键词：打分法、确定评价指标、形成评价体系2、解决评价类问题，首先确定以下三个问题：（1）评价的目标是什么（2）为了达到这个目标有哪几种可选的方案（3）评价的准则或者说指标是什么（我们根据什么东西来评价好坏）。

选拔队员与组队问题摘要：我们通过对每个队员的基本条件进行分析，我们采用了两种方案解决问题。

方案一：考虑队员的个人竞赛技术水平建立模型一，在模型一的基础上，考虑每个对竞赛技术水平建立了非线性优化模型二和模型三。

问题一：通过建立层次模型，计算每个基本条件对队员的竞赛技术水平的权重(0.3649,0.2479,0.1593,0.0999,0.0622,0.0398,0.0261)Tω=，然后得到每个队员的竞赛技术水平并对其排序（见表二），确定被淘汰的队员为H和I。

问题二：通过模型二求得：把G，L，S这三个队员组成一队时，其竞赛技术水平最高值为：9.588150。

问题三：通过模型三我们求得：使整个竞赛技术水平最高的组队方案。

第一队：A，B，L；第二队：E，F，N；第三队：D，J，S；第四队：K，M，R；第五队：G，O，Q；第六队：C，P，T；每个队的竞赛技术水平的值分别为：9.138，8.9618，9.05707，9.36774，9.32846，9.13068。

方案二：考虑每个队的整体竞赛技术水平建立模型四，得到组队方案为第一队：E，F，S；第二队：I，J，K；第三队：B，G，P；第四队：C，N，R；第五队：G，O，Q；第六队：H，L，T；每个队的竞赛技术水平的值分别为：9.133，8.572，9.265，8.844，9.5，9.392。

淘汰的队员为A和O。

在模型四的基础上求解模型二得到：把H，L，G这三个队员组成一队时，其竞赛技术水平最高值为：9.620。

关键字：层次分析法、优化、权重，竞赛技术水平。

Abstract:We have analysed by being in progress to every Y oung Pioneer's main conditions , we have adopt two kinds schemes to solve a problem.Scheme one: Think that Y oung Pioneer's individual contest engineering level builds a model one, think that every has built nonlinearity optimization model two sums models to contest engineering level in the model on one's basis, three.Question one:By the weight building arrangement of ideas model , calculating every main conditions to Y oung Pioneer's contest engineering level,and then, the contest engineering level getting every Y oung Pioneer and Y oung Pioneer who orders the person (be expressed two) , ascertains that to be sifted out are H and I.Question two:By the model, two asks for: When this three Y oung Pioneer are composed of one team with G , L , S, whose maximal contest engineering level value is: 9.588150. Question three:Pass a model three we ask for: Use the team of maximal group of entire contest engineering level scheme. The first team: A , B , L; Second team: E , F , N; Third team: D , J , S; Fourth team: K , M , R; Fifth team: G , O , Q; Sixth team: C , P , T; Every team's contest engineering level value is respectively: 9.138 , 8.9618 , 9.05707 , 9.36774 , 9.32846 , 9.13068.Scheme two:Think that every team's overall contest engineering level builds a model four, are formed the team scheme for the first group: E , F , S; Second team: I , J , K; Third team: B , G , P; Fourth team: C , N , R; Fifth team: G , O , Q; Sixth team: H , L , T; Every team's contest engineering level value is respectively: 9.133 , 8.572 , 9.265 , 8.844 , 9.5 , 9.392. Y oung Pioneer who is sifted out is A and O.Find the solution in the model on four's bases model two: When this three Y oung Pioneer are composed of one team with H , L , G, whose maximal contest engineering level value is: 9.620. Key words:Arrangement of ideas analyses law , optimization , weight , contest engineering level.一问题重述在一年一度的美国MCM和全国大学生竞赛活动中，任何一个参赛院校都会遇到如何选拔队员和科学合理的组队问题。

(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 202011171881.5(22)申请日 2020.10.28(71)申请人 中国兵器科学研究院地址 100089 北京市海淀区车道沟十号院(72)发明人 朱正福　刘英　姬广振　杨春华　李阳　(74)专利代理机构 中国兵器工业集团公司专利中心 11011代理人 刘二格(51)Int.Cl.G06Q 10/06(2012.01)(54)发明名称一种层次分析法平均随机一致性指标RI的计算方法(57)摘要本发明公开了一种层次分析法平均随机一致性指标RI的计算方法，对指数标度法的两两比较重要度进行了约定，构造指数标度法的随机比较矩阵，采用QR方法通过编程求比较矩阵的特征值，并通过多次的特征值计算得到最大特征值的平均值。

本发明给出了指数标度法(e 0/4‑e 8/4)的平均随机一致性指标RI值，该RI值为基于指数标度法的层次分析法的两两比较矩阵是否一致提供了判断依据，为基于指数标度法的层次分析法的应用提供了基础。

权利要求书3页 说明书6页 附图1页CN 112258059 A 2021.01.22C N 112258059A1.一种层次分析法平均随机一致性指标RI的计算方法，其特征在于，包括以下步骤：步骤一，约定指数标度法比较重要度；步骤二，构造随机比较矩阵；步骤三，采用QR方法求比较矩阵A的特征值；步骤四，计算最大特征值的平均值λmax；步骤五，计算随机性指标RI。

2.如权利要求1所述的层次分析法平均随机一致性指标RI的计算方法，其特征在于，所述步骤一中，指数标度法比较重要度为：3.如权利要求2所述的层次分析法平均随机一致性指标RI的计算方法，其特征在于，所述步骤二中，让比较矩阵A中元素的随机地取指数标度(e0/4-e8/4)下的可能值，各对于固定的比较矩阵的阶数n，随机比较矩阵的构造规则为：对于矩阵A的元素a ij，当i<j时，随机地取自e8/4、e7/4、e6/4、e5/4、e4/4、e3/4、e2/4、e1/4、e0/4、1/e1/4、1/e2/4、1/e3/4、1/e4/4、1/e5/4、1/e7/4、1/ e8/4共17个数中的某一个，当i>j时,a ji＝1/a ij，当i＝j时，取1.00。

权重确定方法归纳多指标综合评价是指人们根据不同的评价目的，选择相应的评价形式据此选择多个因素或指标，并通过一定的评价方法将多个评价因素或指标转化为能反映评价对象总体特征的信息，其中评价指标与权重系数确定将直接影响综合评价的结果。

按照权数产生方法的不同多指标综合评价方法可分为主观赋权评价法和客观赋权评价法两大类，其中主观赋权评价法采取定性的方法由专家根据经验进行主观判断而得到权数，然后再对指标进行综合评价，如层次分析法、综合评分法、模糊评价法、指数加权法和成效系数法等。

客观赋权评价法那么根据指标之间的相关关系或各项指标的变异系数来确定权数进行综合评价，如熵值法、神经网络分析法、TOPSIS法、灰色关联分析法、主成分分析法、变异系数法等。

两种赋权方法特点不同，其中主观赋权评价法依据专家经验衡量各指标的相对重要性，有一定的主观随意性，受人为因素的干扰较大，在评价指标较多时难以得到准确的评价。

客观赋权评价法综合考虑各指标间的相互关系，根据各指标所提供的初始信息量来确定权数，能够到达评价结果的精确但是当指标较多时，计算量非常大。

下面就对当前应用较多的评价方法进行阐述。

一、变异系数法〔一〕变异系数法简介变异系数法是直接利用各项指标所包含的信息，通过计算得到指标的权重。

是一种客观赋权的方法。

此方法的根本做法是：在评价指标体系中，指标取值差异越大的指标，也就是越难以实现的指标，这样的指标更能反映被评价单位的差距。

例如，在评价各个国家的经济开展状况时，选择人均国民生产总值(人均GNP)作为评价的标准指标之一，是因为人均GNP不仅能反映各个国家的经济开展水平，还能反映一个国家的现代化程度。

如果各个国家的人均GNP没有多大的差异，那么这个指标用来衡量现代化程度、经济开展水平就失去了意义。

由于评价指标体系中的各项指标的量纲不同，不宜直接比拟其差异程度。

为了消除各项评价指标的量纲不同的影响，需要用各项指标的变异系数来衡量各项指标取值的差异程度。

东南大学《数学实验》报告学号06010314 姓名梅杰成绩实验内容：计算随机一致性指标RI一实验目的计算n=3~30时的n阶矩阵的随机一致性指标RI二预备知识(1)熟悉随机一致性指标的含义及计算方法(2)熟悉eig、rand等Matlab命令三实验内容与要求用MATLAB编制程序，（要求采用和法计算最大特征值），分别计算n=3~30时的n阶矩阵的随机一致性指标RI。

RI=zeros(1,30); %定义结果输出格式并初始化，RI(1)直接赋值为0 for n=3:30 %循环计算阶数3到30的随机正互反矩阵的RI %n=20; %起初以20阶矩阵为例测试times=10000; %10000个子样，应该够多了吧enum=[9 8 7 6 5 4 3 2 1 1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9]; %矩阵元素从enum中取得lamda = zeros(1, times); %最大特征值向量初始化A=ones(n,n); %初始化相应阶数的矩阵for num=1:times %循环for i=1:n %把矩阵A赋值为正互反矩阵for j=i+1:nA(i,j)=enum(ceil(17*rand(1))); %矩阵的上半部分从enum中随机取值A(j,i)=1/A(i,j); %矩阵的下半部分与上半部分成倒数A(i,i)=1; %矩阵对角线为1 endendV=eig(A); %求得A的特征向量lamda(num)=max(V); %以最大特征值给lamda向量赋值endk=sum(lamda)/times; %最大特征值的平均值RI(n)=(k-n)/(n-1); %得出对应的RI(n) endRI %最后输出RI向量，即1－30阶矩阵的平均随机一致性指标四实验心得一开始对matlab命令不熟悉，感觉无从下手，通过查阅matlab 相关资料，进一步了解matlab后，找到门路和方法，由于对程序和函数的不熟悉，又花费了大量时间，不过终有所获。

2
1
1
3 1 1
权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T
一致性指标 CI 5.073 5 0.018 5 1
随机一致性指标 RI=1.12 (查表)
通过一致
一致性比率CR=0.018/1.12=0.016<0.1
性检验
正互反阵最大特征根和特征向量的简化计算
总排序具有满意的一致性，否则需要重新调整那些一致性比 率高的判断矩阵的元素取值。
到此，根据最下层（决策层）的层次总排序做出最后决策。
选择旅游地 记第2层（准则）对第1层（目标）的权向量为
w(2) (0.263, 0.475, 0.055, 0.090, 0.110)T
同样求第3层(方案)对第2层每一元素(准则)的权向量
一致性检验：利用一致性指标和一致性比率<0.1
及随机一致性指标的数值表，对 A进行检验的过程。
“选择旅游地”中 准则层对目标的权 向量及一致性检验
最大特征根=5.073
准则层对目标的成对比较阵
1 1/ 2
2
1
A 1/ 4 1/ 7
1/ 3
1/ 5
1/ 3 1/ 5
4 3 3
7
5
5
1 1/ 2 1/ 3
作业：某公司有一笔资金可用于4种方案 ：投资 房地产，购买股票，投资工业和高技术产业。评 价和选择投资方案的标准是：收益大，风险低和 周转快。试对4种投资方案做出分析和评价。
根据题意建立AHP的多级递阶结构
建立判断矩阵，计算各级要素相对重要度并进行一致性检验
计算综合重要度
结论
对总目标Z的排序为
A1
A2

[V,D]=eig(a);
tbmax=max(D(:));
L=tbmax;
CI=(L-n)/(n-1);
end
CR=CI/0.58;
clear
forn=3
a=[1 1/5 1/3;5 1 3;3 1/3 1];
[V,D]=eig(a);
tbmax=max(D(:));
L=tbmax;
CI=(L-n)/(n-1);
1.6157 1.6245 1.6334 1.6410 1.6480 1.6542 1.6581 14 1.6710 1.6754 1.6779 1.6825 1.6836
（2）建立一个AHP模型，并将结果填入下表
AHP模型
模型解释
现有一学生考虑出国读研，目前可供选择的学校有：学校甲、学校乙，学校丙。
选择最佳的学校为的是获得更好的学习机会，目的都是相同的，因此可以利用层次分析法来建立模型。
准侧：C1学费C2学校实力
C3地理位置
目标层合理选择国外大学
准则层学费学校实力地理位置
方案层学校甲学校乙学校丙
判断矩阵表：
Z C1 C2 C3
C1 1 1/9 1/4
C2 9 1 9
C3 4 1/91
最大特征值为：3.0385
Columns 1 through 8
0 0 0.5246 0.8676 1.0795 1.2227 1.3232 1.3927
Columns 9 through 16
1.4436 1.4853 1.5158 1.5401 1.5610 1.5775 1.5919 1.6067
Columns 17 through 24
fori=1:n
forj=i:n

评价模型评价类数学模型是全国数学建模竞赛中经常出现的一类模型，如2005年全国赛A题长江水质的评价问题，2008年B题高校学费标准评价体系问题等。

主要介绍三种比较常用的评价模型：层次分析模型，模糊综合评价模型，灰色关联分析模型，以期帮助大家了解不同背景下不同评价方法的应用。

层次分析模型层次分析法(AHP)是根据问题的性质和要求，将所包含的因素进行分类，一般按目标层、准则层和子准则层排列，构成一个层次结构，对同层次内诸因素采用两两比较的方法确定出相对于上一层目标的权重，这样层层分析下去，直到最后一层，给出所有因素相对于总目标而言，按重要性程度的一个排序。

其主要特征是，它合理地将定性与定量决策结合起来，按照思维、心理的规律把决策过程层次化、数量化。

运用层次分析法进行决策，可以分为以下四个步骤：步骤1 建立层次分析结构模型深入分析实际问题，将有关因素自上而下分层(目标—准则或指标—方案或对象)，上层受下层影响，而层内各因素基本上相对独立。

步骤2构造成对比较阵对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，借助1~9尺度，构造比较矩阵；步骤3计算权向量并作一致性检验由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验，若通过，则最大特征根对应的特征向量做为权向量。

步骤4计算组合权向量(作组合一致性检验)组合权向量可作为决策的定量依据通过一个具体的例子介绍层次分析模型的应用。

例(选择旅游地决策问题)如何在桂林、黄山、北戴河3个目的地中按照景色、费用、居住条件、饮食、旅途条件等因素进行选择。

步骤1 建立系统的递阶层次结构将决策问题分为3个层次：目标层O，准则层C，方案层P；每层有若干元素，各层元素间的关系用相连的直线表示。

图1 选择旅游地的层次结构步骤2构造比较矩阵元素之间两两对比，对比采用美国运筹学家A.L.Saaty 教授提出的1~9比率标度法(表1)对不同指标进行两两比较，构造判断矩阵。

2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）D题对学生宿舍设计方案的评价学生宿舍事关学生在校期间的生活品质, 直接或间接地影响到学生的生活、学习和健康成长。

学生宿舍的使用面积、布局和设施配置等的设计既要让学生生活舒适，也要方便管理, 同时要考虑成本和收费的平衡, 这些还与所在城市的地域、区位、文化习俗和经济发展水平有关。

因此，学生宿舍的设计必须考虑经济性、舒适性和安全性等问题。

经济性：建设成本、运行成本和收费标准等。

舒适性：人均面积、使用方便、互不干扰、采光和通风等。

安全性：人员疏散和防盗等。

附件是四种比较典型的学生宿舍的设计方案。

请你们用数学建模的方法就它们的经济性、舒适性和安全性作出综合量化评价和比较。

对学生宿舍设计方案的评价摘要本文主要从经济性、舒适性、安全性三个方面对四种学生宿舍的设计方案做出综合量化和比较。

在评价过程中，主要运用了模糊决策和层次分析法，并利用MATLAB 软件进行求解。

由于本问题的许多条件比较模糊，具有隐藏性，我们先对附件中的数据进行预处理，从中提取与评价相关的因素，然后利用层次分析法确定各准则对目标的权重，从而建立学生宿舍设计方案的评价模型。

具体结果为：（1）经济性方面：得出四种学生宿舍设计方案在此方面的的组合权向量为： )1668.0,2265.0,5627.0,0440.0(，根据指标越小，优先选择程度越大的准则得出：方案1是经济性最优的，其次为方案4、方案3，最后为方案2。

（2）舒适性方面：得到组合权向量为：)1999.0,1576.0,5301.0,1124.0(，根据指标越大，优先选择程度越大的准则得出：方案2是舒适度最高的，其次为方案4、方案3，最后为方案1。

（3）安全性方面：得到组合权向量为：)2223.0,2684.0,4158.0,0935.0(，利用和（2）同样的准则，得出了方案2是安全性最强的，其次为方案3、方案4，最后为方案1。

实验报告（一）课程名称数学建模实验项目Matlab基本操作及其实际应用实验环境PC机、Matlab学院/班级学号/姓名指导教师实验日期成绩一、实验名称：随机一致性指标求解二、实验目的：1）掌握用matlab求解随机一致性指标的方法2）加深对随机一致性指标概念的理解三、实验内容：用matlab或C++编写程序分别计算n=3-30时的n阶矩阵的随机一致性检验指标的值RI。

//本组实验随机数产生正互反矩阵,这个数目必须取的相当大（超过1000000，所以此程序跑起来比较费时），才比较接近标准答案#include<iostream>#include<cmath>#include<ctime>#include<cstdlib>#include<iomanip>using namespace std;int getNameta(double a[],int n); //获取当前随机正互反矩阵的最大λvoid createMatrix(double a[],int n); //建立随机正互反矩阵int getMax(double b[],int n); //获取b矩阵中的最大值void Mifa(double a[],double b[],int n); //幂法过程void main(){int n; //矩阵阶数int m = 3000; //建立的随机正互反矩阵个数int all = 0; //所有最大λ的和int tem = 0;int ri = 0; //最终的RI（为了计算方便，将实际的RI扩大了100倍进行计算了）cout << "Please enter the size of the matrix:" << endl;cout << "n = " ;cin >> n;if(n > 2&& n <= 30){for(int i =0;i<m;i++){double *a = new double[n*n]; //声明n*n的随机正互反矩阵for(int j =0;j<n*n;j++){a[j] = 1;}createMatrix(a,n); //建立n*n的随机正互反矩阵all += getNameta(a,n); //获得最大λ}tem = all/m;//计算得RIri = (tem - n*100);ri = ri/(n-1); //计算得到的RI （乘以100后的结果）int baiwei = ri/100;int shiwei = (ri-100*baiwei)/10;int gewei = ri-100*baiwei-10*shiwei;cout << "The RI of the " << n <<" size matrix is " << baiwei << "." << shiwei << gewei<< endl;}else if(n ==1){cout << "The RI of the " << n <<" size matrix is " << 0 << endl;}elsecout << "The size of n you input is wrong" << endl;}void createMatrix(double a[],int n){doublesample[17]={1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,1.0/2.0,1.0/3.0,1.0/4.0,1.0/ 5.0,1.0/6.0,1.0/7.0,1.0/8.0,1.0/9.0};for(int i=0;i<n;i++)for(int j=i;j<n;j++){int t;t = rand()%17;if( j == i){a[n*i+j]=1.0;}else{a[n*i+j] = sample[t];a[n*j+i] = 1.0/sample[t];}}}int getNameta(double a[],int n){int tem=0;double *b=new double[n];for(int i=0;i<n;i++){b[i]=1.0/n;}Mifa(a,b,n);int max=getMax(b,n);while(tem != max){tem = max;for(int d = 0;d<n;d++){b[d] = b[d]*100/max;}Mifa(a,b,n);max = getMax(b,n);}int nameta;nameta = tem;return nameta;}void Mifa(double a[],double b[],int n) {double *c = new double[n];for(int r = 0;r<n;r++){c[r] = 0.0;}for(int i =0;i<n;i++)for(int j = 0 ;j<n;j++){c[i] += a[n*i+j]*b[j];}for(int k =0;k<n;k++){b[k] = c[k];}}int getMax(double b[],int n){int a = 0;for(int i = 0;i<n;i++){if(100*b[i]>a)a = 100*b[i];}int tem;tem = a;return tem;}实验结果：四、实验心得：本实验使用的是C++编制程序，令我更好的理解随机一致性指标RI，进一步掌握了随机一致性指标求解方法以及随机一致性检验的方法。

层次分析法原理及计算过程详解写在前面：层次分析法是一个很早的决策算法了，它能够处理多目标多准则的决策问题，思维方式却很简单。

由于其系统性等优点，后续很多算法都有借鉴，所以这里写一写。

网上关于该方法的讲解很多也很详细，所以本篇都是在前辈的基础上进行整理加工。

文章尽量详细，然后加上一些我自己的理解，希望后面看到的人能够读起来更轻松，更容易接受。

注意：文中说的判断矩阵，又称成对比较阵目录：1.层次分析法概论1.2什么是决策1.3 决策分析法原理2.层次分析法的基本步骤2.1 层次分析法步骤2.2 建立层次结构模型2.3 构造判断矩阵2.4 计算单层权向量并做一致性检验2.5 计算组合权向量(层次总排序)并做一致性检验2.6 层次分析法基本步骤归纳3. 层次分析法的优缺点3.1 层次分析法的优点4.注意事项5.可应用的领域6. 完整例子分析6.1 旅游问题6.2 干部选择问题1.层次分析法概论1.1 什么是层次分析法层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代初期由美国匹兹堡大学运筹学家托马斯·塞蒂（T.L. Saaty）在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”的课题时提出。

它是一种应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。

是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

是对社会、经济以及管理领域的问题进行系统分析时，面临的经常是一个由相互关联、相互制约的众多因素构成的复杂系统。

层次分析法则为研究这类复杂的系统，提供了一种新的、简洁的、实用的决策方法。

是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。

该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。