层次分析法中高阶平均随机一致性指标_RI_的计算

层次分析法在汽车零件供应商评估中的应用本文以某大型汽车制造企业零件供应商选择为例，设计了在汽车零件供应商选择过程中甄选最优者的指标体系，在评估方法上，采取定性与定量相结合的方法，运用层次分析法(AHP)确定了指标权重系数，并通过一致性检验，证明所建立的供应商甄选评估体系是实际可操作的。

标签：层次分析法供应商评价一、汽车零件供应商评价指标设计利用AHP法对汽车零件供应商评估进行分析，可建立三个层次的结构模型，即评估内容层、评估目标层、评估指标层。

评估内容层是指评估所指向的具体对象与范围，它具有相对性。

对于不同的零件供应商评估内容存在差异。

评估内容层中的元素是对汽车零件供应商进行评估的内容。

笔者设计的汽车零件供应商测评内容主要包括:质量、价格、技术、服务、创新。

评估项目层是根据评估内容的要求给出的，是对评估内容的具体规定。

如技术内容，要通过以下评估项目：通用化、模块化、电子及职能化、环保化、轻量化来体现。

而技术只是对评估项目的一个综合说明。

测评项目的选择要通过一定的定量分析方法来实现，不能任意的指定。

一般采用德尔菲咨询、问卷调查与层次分析法、多元分析法进行选择。

评估指标层是评估项目层的可操作化的表现形式。

对于每一个测评指标都必须认真分析研究，给予清楚、准确的表述，使评估各方均能明确评估指标的涵义，不会因对测评指标的不同理解而导致标准不一产生评估结果误差。

选择评估指标时不但要求要具有实际价值，还要是切实可行的，最好是能够量化的。

二、分别构造判断矩阵本文只针对项目层进行讨论，根据表2，对各指标进行两两比较，采用层次分析法，确定其权重，构造出判断矩阵。

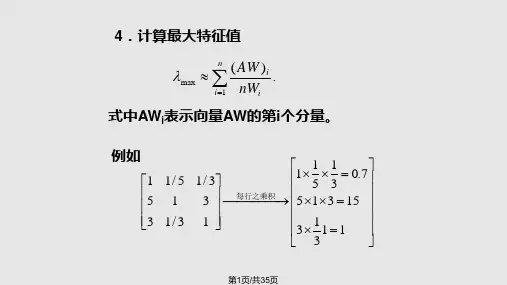
（表3～表4）注:（确定价格、技术、服务、创新等指标评估的判断矩阵及权重方法同上，不再列举）三、确定各指标权重1.首先将判断矩阵的每一列元素作归一化处理，其元素的一般项为:2.将各列归一化后的判断矩阵按行相加3.再将向量归一化，得到得到的W=[W1,W2,…,Wn]T即为所求特征向量。

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。

其中A为判断矩阵，不同的标度和评定A将不同。

m为A的维数RI为判断矩阵的平均随机一致性指标：根据m的不同值不同。

当CR<0.1时符合一致性检验，判断矩阵构造合理。

下面是层次分析法的简介，以及判断矩阵构造方法。

一.层次分析法的含义层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.Saaty）正式提出。

它是一种定性和定量相结合的、系统化、层次化的分析方法。

由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。

它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。

（1）层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。

层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

江苏科技信息February 2012表2判断矩阵摘要：文章介绍了层次分析法确定评价指标权重的过程和计算方法，建立的Excel 计算模板操作简单，方便推广，具有较强的实用性。

关键词：决策分析法；层次分析法；权重；Excel ；计算模板作者简介：曹茂林，扬州市环境监测中心站，高级工程师；研究方向：环境监测技术与环境科技管理。

■曹茂林层次分析法确定评价指标权重及Excel 计算层次分析法（Analytic hierarchy process ，简称AHP 法）是美国运筹学家T.L.Saaty 等人在20世纪70年代中期提出了一种定性和定量相结合的，系统性、层次化的多目标决策分析方法。

在环境科研实践中，AHP 法广泛应用于生态安全[1]、环境规划[2]、区域承载力[3]、化学品环境性能评价[4]等众多领域。

AHP 法的核心是将决策者的经验判断定量化，增强了决策依据的准确性，在目标结构较为复杂且缺乏统计数据的情况下更为实用。

应用AHP 法确定评价指标的权重，就是在建立有序递阶的指标体系的基础上，通过比较同一层次各指标的相对重要性来综合计算指标的权重系数。

具体步骤如下：1.构造判断矩阵同一层次内n 个指标相对重要性的判断由若干位专家完成。

依据心理学研究得出的“人区分信息等级的极限能力为7±2”的结论，AHP 法在对指标的相对重要性进行评判时，引入了九分位的比例标度，见表1。

判断矩阵A 中各元素a ij 为i 行指标相对j 列指标进行重要性两两比较的值。

显然，在判断矩阵A 中，a ij ＞0，a ii ＝1，a ij ＝1/a ji （其中i ，j=1,2,…，n ）。

因此，判断矩阵A 是一个正交矩阵，左上至右下对角线位置上的元素为1，其两侧对称位置上的元素互为倒数。

每次判断时，只需要作n(n-1)/2次比较即可。

表2是一个7阶判断矩阵，本文以此为例介绍应用Excel 计算指标权重并进行一致性检验的方法。

function [w,CR]=mycom(A,m,RI)[x,lumda]=eig(A);r=abs(sum(lumda));n=find(r==max(r));max_lumda_A=lumda(n,n);max_x_A=x(:,n);w=A/sum(A);CR=(max_lumda_A-m)/(m-1)/RI;end本matlab程序用于层次分析法中计算判断矩阵给出的权值已经进行一致性检验。

其中A为判断矩阵，不同的标度和评定A将不同。

m为A的维数RI为判断矩阵的平均随机一致性指标：根据m的不同值不同。

当CR<0.1时符合一致性检验，判断矩阵构造合理。

下面是层次分析法的简介，以及判断矩阵构造方法。

一.层次分析法的含义层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.Saaty）正式提出。

它是一种定性和定量相结合的、系统化、层次化的分析方法。

由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。

它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

二.层次分析法的基本思路与人对一个复杂的决策问题的思维、判断过程大体上是一样的。

（1）层次分析法的原理层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。

层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

AHP法在确定绩效考核指标权重的应用摘要：人力资源绩效评价的选择关键在于权重的确定，如何确定绩效考核指标的权重是建立绩效考核体系过程中一个非常重要的环节。

本文通过介绍绩效考核指标权重以及针对具体实例采用层次分析法确定绩效考核指标的步骤，以期达到运用AHP法来提高绩效考核指标权重确定的科学性和准确性的目的。

关键词：绩效考核；考核指标；权重；层次分析法1．引言现实的员工绩效评价工作中存在许多应当改进的方面，如指标怎样确立才更公平、怎样做到合理量化、权重如何分配更准确等。

本文建立相对完善的评价指标体系，以层次分析法为基础构建矩阵，解决排序问题即权重问题，并通过一致性检验，建立员工绩效综合评价模型以解决实际工作中的难题。

国内企业普遍存在基础管理薄弱，缺乏历史资料的问题，尤其是在非财务指标方面，以前大多没有进行过这些方面的考核，也就没有数据的积累，不具备应用客观赋权法的基础条件。

再者，从心理学角度看，人们对自己承诺的事情会加倍努力去做。

因此，让有代表性的管理者和员工参与到指标权重的制定中来，会比通过复杂的计算而大家根本不了解它是怎么来的要有意义，更能激发员工贯彻绩效考核标准的主动性。

有鉴于此，选择主观赋权法更为合理实用、有效。

本文为提高考评结果的可比性与客观性，针对具体的实例，采用了集定量与定性于一身的层次分析法(AHP法)来确定绩效考核指标权重系数，以期达到提高科学性、客观性和可比性等的目的。

2．绩效考核指标权重及其设置的意义确定完整、合理的绩效考核指标是绩效考核的重要前提，但真正的难点是确定每个指标的权重。

如何确定绩效考核指标的权重是建立绩效考核体系过程中一个非常重要而又值得研究的环节。

权重是绩效指标体系的重要组成部分，通过对每个被评估者职位性质、工作特点及对经营业务的控制和影响等因素的分析，确定每类及每项指标、工作目标设定整体及其中各项在整个指标体系中的重要程度，赋予相应的权重，以达到考核的科学合理。

层次分析法中高阶平均随机一致性指标(RI)的计算
洪志国;李焱;范植华;王勇
【期刊名称】《计算机工程与应用》
【年(卷),期】2002(038)012
【摘要】利用层次分析法分析和解决问题时,要对通过两两比较判断出的矩阵一致性进行检验[1].高阶平均随机一致性指标的值一般无法直接通过查表而得,这一难点阻碍着层次分析法大面积的推广应用[2].文章在深刻剖析层次分析法的基础上,给出根据平均随机一致性指标的定义计算高阶平均随机一致性指标值的算法,并且基于windows环境在delphi6.0下予以程序实现.该算法已成功运用于中国科学院知识创新工程某智能决策系统中.
【总页数】4页(P45-47，150)
【作者】洪志国;李焱;范植华;王勇
【作者单位】中国科学院软件所GSL实验室,北京,100080;中国科学技术大学计算机系,合肥,230027;中国科学院软件所GSL实验室,北京,100080;中国科学院软件所GSL实验室,北京,100080
【正文语种】中文
【中图分类】TP18
【相关文献】
1.关于平均随机一致性指标的新定义方法 [J], 孙水玲
2.层次分析法中平均随机一致性指标的数学软件实现 [J], 陈晓江
3.AHP法中平均随机一致性指标的算法及MATLAB实现 [J], 焦树锋
4.马氏环境中树指标马氏链随机转移概率调和平均的强极限性质 [J], 石志岩;鲍丹;吴佰慧
5.等距数列平均指标计算方法研究——兼评“中位数总是介于算术平均数和众数之间吗?”一文中的一个错误结论 [J], 朱(鱼它)华
因版权原因，仅展示原文概要，查看原文内容请购买。

试论层次分析法（AHP）在公共部门绩效考核指标权重确定中的运用龙朝双 陈志刚董建涛【摘要】公共部门的绩效考核实施起来困难重重，有组织本身的原因，也有方法技术方面的原因。

为应对考核技术的不足，本文试图引入AHP方法来确定考核指标的权重，以增强考核的科学性。

在文章的后面附以层次分析法如何确定公共部门绩效考核指标权重的实例，以资参考。

【关键词】绩效考核 权重 AHP【中文图书分类号】D035 【文献标识号】A1 问题的提出随着全球化的扩张和经济的迅猛发展,传统的官僚制模式之弊端日益凸显,并导致政府面临严重的财政危机、管理危机、信任危机以及合法性危机。

西方各国为了摆脱政府管理的困境,改变过去的政府管理过程导向，加强了对结果的关注。

正是这种转变带来了西方公共部门绩效考核蓬勃发展。

其标志是克莱伦斯·雷德和赫伯特·西蒙的《市政工作衡量:行政管理评估标准的调查》一书。

20世纪70年代初，美国尼克松政府便开始了大规模的公共部门绩效评估，在随后的福特政府、布什政府得到了进一步发展，在国外政府绩效评估热潮的影响和推动下,我国政府和学术界也开始关注和重视政府绩效的评估问题。

2002年厦门思明区政府与厦门大学共同开发了“公共部门绩效评估系统”。

人事部《中国政府绩效评估研究》课题组提出了一套我国地方政府绩效评估指标体系,该评估体系由职能指标、影响指标和潜力指标3个一级指标,11个二级指标以及33个三级指标构成。

在公共部门绩效考核浪潮冲击着传统官僚制政府模式的同时，我们也必须认识到由于公共组织自身的特点以及考核人员方法、技术的不足为考核带来了诸多障碍，其主要包括： 1.1 公共组织特征下的绩效考核困境（1）非市场产出的公共部门的产出大多难以量化政府部门的产品或服务通常是一些非商品性的产出,它们进入市场的交易体系后很难形成一个反映其生产成本的货币价格,从而造成对其进行准确测量的技术上的难度。

政府提供公共物品或服务更具垄断性,这样也不太容易通过横向比较来测度政府部门的绩效。

层次分析法介绍一、首先确定模型的组成此次模型是为了确定物流配送中心的选址问题。

其中物流配送中心的选址是目标层；因素层包括交通条件；经济环境；配套条件；人口条件和生产规模。

方案层分为三个县，每个县拥有不同的条件资源，分别为A县、B县、C县。

假设因素层对目标层的影响：交通条件的影响为1；并以交通条件为基准，经济环境对交通条件的重要性为3；配套条件对交通条件的重要性为1/2；人口条件对交通条件的重要性为1/4；生产规模对交通条件的重要性为5，建立矩阵。

目标-因素交通（Y1）经济（Y2）配套（Y3）人口（Y4）规模（Y5）交通（Y1）15=1/342经济（Y2）=1/51=1/15=4/5=2/5配套（Y3）3151126人口（Y4）=1/4=5/4=1/121=1/2规模（Y5）=1/2=5/2=1/621权向量：Y1=1*5*1/3*4*2=13.3；Y2=0.0053；Y3=3240；Y4=0.013；Y5=0.42。

计算W1= 5Y1=1.68；同理得出：W2=0.35；W3=5.04；W4=0.42；W5=0.84。

对上述W1、W2、W3、W4、W5进行均一化W1=0.2 W2=0.04 W3 =0.61 W4=0.05 W5=0.1特征向量={W1，W2，W3，W4，W5}T；AW=目标因素矩阵*{W1，W2，W3，W4，W5}T；利用Excel软件计算最大特征根。

AW1=（1*0.2+5*0.04+1/3*0.61+4*0.05+2*0.1）/（5*0.2）=1.01AW2=（1/5*0.2+1*0.04+1/15*0.61+4/5*0.05+2/4*0.1）/（5*0.04）=1.01 AW3=（3*0.2+15*0.04+1*0.61+12*0.05+6*0.1）/（5*0.61）=1.01 AW4=（1/4*0.2+5/4*0.04+1/12*0.61+1*0.05+1/2*0.1）/（5*0.05）=1.01 AW5=（1/2*0.2+5/2*0.04+1/6*0.61+2*0.05+1*0.1）/（5*0.1）=1.01λmax=（AW1+AW2+AW3+AW4+AW5+AW6）=5.05一致性检验：CI=（5.05-5）/（5-1）=0.0125；RI查表得知为：1.12；CR=0.0125/1.12=0.011<0.01；由此得出，目标的不一致性在可允许的范围内，目标对影响因素的一致性检验有效。

(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号 (43)申请公布日 (21)申请号 202011171881.5(22)申请日 2020.10.28(71)申请人 中国兵器科学研究院地址 100089 北京市海淀区车道沟十号院(72)发明人 朱正福　刘英　姬广振　杨春华　李阳　(74)专利代理机构 中国兵器工业集团公司专利中心 11011代理人 刘二格(51)Int.Cl.G06Q 10/06(2012.01)(54)发明名称一种层次分析法平均随机一致性指标RI的计算方法(57)摘要本发明公开了一种层次分析法平均随机一致性指标RI的计算方法，对指数标度法的两两比较重要度进行了约定，构造指数标度法的随机比较矩阵，采用QR方法通过编程求比较矩阵的特征值，并通过多次的特征值计算得到最大特征值的平均值。

本发明给出了指数标度法(e 0/4‑e 8/4)的平均随机一致性指标RI值，该RI值为基于指数标度法的层次分析法的两两比较矩阵是否一致提供了判断依据，为基于指数标度法的层次分析法的应用提供了基础。

权利要求书3页 说明书6页 附图1页CN 112258059 A 2021.01.22C N 112258059A1.一种层次分析法平均随机一致性指标RI的计算方法，其特征在于，包括以下步骤：步骤一，约定指数标度法比较重要度；步骤二，构造随机比较矩阵；步骤三，采用QR方法求比较矩阵A的特征值；步骤四，计算最大特征值的平均值λmax；步骤五，计算随机性指标RI。

2.如权利要求1所述的层次分析法平均随机一致性指标RI的计算方法，其特征在于，所述步骤一中，指数标度法比较重要度为：3.如权利要求2所述的层次分析法平均随机一致性指标RI的计算方法，其特征在于，所述步骤二中，让比较矩阵A中元素的随机地取指数标度(e0/4-e8/4)下的可能值，各对于固定的比较矩阵的阶数n，随机比较矩阵的构造规则为：对于矩阵A的元素a ij，当i<j时，随机地取自e8/4、e7/4、e6/4、e5/4、e4/4、e3/4、e2/4、e1/4、e0/4、1/e1/4、1/e2/4、1/e3/4、1/e4/4、1/e5/4、1/e7/4、1/ e8/4共17个数中的某一个，当i>j时,a ji＝1/a ij，当i＝j时，取1.00。

层次分析法一致性检验层次分析法(Analytic Hierarchy Process，简称AHP)是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。

它是美国运筹学家T. L. Saaty 教授于70 年代初期提出的一种简便、灵活而又实用的多准则决策方法。

?1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。

层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

运用层次分析法建模，大体上可按下面四个步骤进行: (i)建立递阶层次结构模型; (ii)构造出各层次中的所有判断矩阵; (iii)层次单排序及一致性检验; (iv)层次总排序及一致性检验。

下面分别说明这四个步骤的实现过程。

1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。

在这个模型下，复杂问题被分解为元素的组成部分。

这些元素又按其属性及关系形成若干层次。

上一层次的元素作为准则对下一层次有关元素起支配作用。

这些层次可以分为三类: (i)最高层:这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。

(ii)中间层:这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包to East for the neijiang-Kunming highway bridge across the River, maming Creek Bridge, pond bridge, bridge, rongzhou bridge, and South Bridge. There are two bridges across the minjiang River: minjiang River Bridge on neikun highway bridge. Inner-city transportation: Shu Nan road, binjiang road, North Road, the minjiang River, the Yangtze River Road, lingang括所需考虑的准则、子准则，因此也称为准则层。

层次分析法在军事情报质量评估中的应用王 海 程立斌作者简介:王 海,男,1977年生,博士研究生,研究方向为情报综合处理;程立斌,男,1977年生,博士研究生,研究方向为情报与指挥自动化。

(合肥电子工程学院 合肥 230037)摘 要 军事情报评估可以及时、全面地发现情报工作中存在的问题,进而能了解组织指挥、装备性能、阵地选择等方面的问题,从而能针对问题采取相应的对策。

因此,军事情报评估是推动情报工作发展的一个重要动力,而层次分析法是定量与定性分析相结合,可对情报进行相对客观评估的一种有效方法。

关键词 军事情报 质量评估 层次分析法层次分析法(Ana1ytic Hierarchy Process,简称AHP 法)是美国运筹学家、匹兹堡大学教授T.L.Saaty 于20世纪70年代提出的一种简便、灵活而又实用的多准则决策方法。

它是一种对较为模糊或较为复杂的决策问题使用定性与定量分析相结合的手段做出决策的简易方法,特别是将决策者的经验判断给予量化,它将人们的思维过程层次化,逐层比较相关因素,逐层检验比较结果的合理性,由此提供较有说服力的依据。

很多决策问题通常表现为一组方案的排序问题,这类问题就可以用AHP 法解决。

近几年来,此法在国内外得到了广泛的应用。

1 军事情报质量评估的意义情报质量评估是指对情报的可靠性、作战价值等进行分析、判断的过程,通过对情报的评估,确定现在需要执行的任务,以及需要做哪些必要的调整;同时,客观的情报评估也有助于激发各情报单位工作的积极性。

军事情报的作用在于削除或减少战场的不确定性,但对于一份具体的军事情报,它是否真正减少了指挥员对战场认识的不确定性?它把战场不确定性减少到何种程度?情报是否可用?使用这份情报会带来多大的风险?这些问题都是指挥员十分关心的问题。

而解决这些问题的途径之一就是通过情报评估的方式。

从原则上说,情报只有通过评估来判定情报是真实、可靠的以后,相关的情报才能使用。

∗收稿日期：2020年12月11日，修回日期：2021年1月23日基金项目：国家社会科学基金军事学项目“陆军战役军团远程机动后勤保障研究”（编号：12GJ003-082）资助。

作者简介：王红旗，男，硕士，副教授，研究方向：军事后勤学。

牟泽龙，男，博士研究生，研究方向：计算机仿真建模。

郭亚子，男，硕士研究生，研究方向：军事后勤学。

1引言随着现代无人机［1］技术的迅速发展与战争形态的升级，许多西方国家正在探索将无人机应用于军事后勤领域。

例如美国在伊拉克战争和阿富汗战争中意识到，常规后勤保障在山区中具有难以行进、易受打击、成本偏高等不利因素，因此美军开始研究更加安全、经济、能重复利用、设计灵活的无人机精确保障手段，并将其列入无人机发展规划中的重点内容之一［2］。

无人机的简易、灵活、低风险等优势使其能有效满足未来战场中后勤精确保障的需求。

任何一种武器装备都需要进行效能评估［3］，这也是现代军事和作战问题研究的一项重要内容。

武器装备的效能评估一般利用建模仿真的方法，考虑装备平时和战时的使用场景，以装备的可用性、可信性、固有能力等作为输入对保障效能进行实时的评价和优化。

对于军用后勤保障无人机，其研发和使用需要巨大的资金投入，为使无人机装备的保障效能得到最大程度的发挥，提升其效能费用比，同时明确我方的实际无人机保障能力，有必要建立一套无人机精确保障效能的评估模型，对无人机进行合理的保障效能评估。

基于此，本文首先根据无人机的使用经验构建无人机精确保障能力的指标体系，接着采用层次分析法［4~5］确定保障能力体系中各项指标的权重系数，然后使用模糊综合评价基于层次分析与模糊综合评价的无人机精确保障效能评估∗王红旗牟泽龙郭亚子（陆军勤务学院重庆401331）摘要无人机精确保障在未来的后勤领域有着广阔的应用空间。

针对无人机精确保障的效能评估，运用层次分析法和模糊综合评价，建立无人机精确保障效能的评价指标体系，确定每项指标的权重，以某机型为例进行量化的具体评价，为精确保障无人机的研制和使用提供了定量的依据。