当前位置：文档之家 › 质点角动量及其守恒定律

质点角动量及其守恒定律

  • 格式：pptx
  • 大小：303.42 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

角动量及其守恒定律

角动量及其守恒定律

m r2 r1 J0
22
因为 1 2， 1 1 2 E k 1 J 1 1 ( J 1 1 ) 1 2 2 相 E k1 E k 2 等 1 1 2 E k 2 J 2 2 ( J 2 2 ) 2 2 2 即系统的机械能不守恒。
23
人双臂收回过程中，内力做功，
J 2
l/2
r dr
2
1 12
l
3
0

1 12
ml
2
如转轴过端点垂直于棒 l 1 2 J r d r ml 2 0 3
例3 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 ， 在盘上取半径为 r ，宽为 d r 的圆环
v M (2 gh )
u l 2
1 2
M

h N
B
l 2 1 12
2
2
把M、N和跷板作为 一个系统, 角动量守恒
mvM l 2 J 2 mu
C l
m l 1 2 1 6 m ( 2 gh )
A l/2
ml
2
解得

mvMl 2 m l
2
2
12 ml
2
2 2 2
质量连续分布刚体的转动惯量
J
m
j
j j
r
2
r dm
2
d m ：质量元
例2 一质量为 m 、长为 l 的均匀细长棒，求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
dr
l 2
r
dr
O´

45--质点的角动量-角动量守恒定律

45--质点的角动量-角动量守恒定律

v0 r0 r1
A
1 2
mv12
1 2
mv02
1 2
mv02
r02 r12
1
6
质点的角动量 角动量守恒定律
1
一.角动量
质点对一固定参考点的
角L动量r：
P
r
mv
L o r m
θ P
p
大小：L＝ r m v sin
方向：右手螺旋定则判定
L
r
p
注意：
a) 必须指明是对谁的角动量；
LP or
b)作圆周运动的质点的角动量 L＝ r m v
c)角动量是描述转动状态的物理量；
d)质点的角动量又称为动量矩。
2
二.质点角动量定理
力对一固定参考点的力矩
M
r
F
r是P点相对于固定点O的位矢。
M or
d
F
θ
p
大小：M＝F r sin
方向：右手螺旋定则判定
M
r
F
将角动量对时间求导，有：
dL dt
ddt(r
mv)
dr dt
mv
r
dmv dt
r
F
得到
M
dL
dt
F
dP
dt
3
将
M
dL
两边同时乘以 dt ，得：
5
例、质量为m的小球系在绳子的一端，绳穿过 光滑水平面上一小孔，使小球限制在水平面上 运动。先使小球以速度v0绕小孔作半径为r0的 圆周运动，然后缓慢向下拉绳使圆周半径减小
为r1，求：（1）小球距管心r1时的速度；（2） 由r0缩短到r1过程中拉绳作的功。
解：角动量守恒

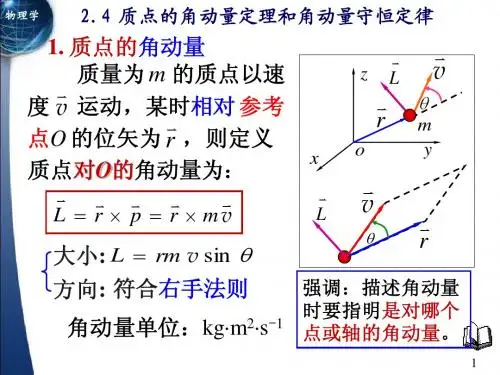
2.4质点的角动量定理和角动量守恒定律

2.4质点的角动量定理和角动量守恒定律

t1
质点的角动量定理：对同一参考点O，质点 所受的冲量矩等于质点角动量的增量.
M 0,
例 2-6
四. 质点的角动量守恒定律
L 恒矢量 （有心力作用）
7
作用于质点的合外力对参考点 O 的力矩，等 于质点对该点 O 的角动量随时间的变化率. 强调：力矩和角动量都是相对同一个参考点的。
6
dL
dm v
dr
物理学
M
dL
t1 dt t2 M d t ：力矩对给定点的冲量，称为冲量矩

t2
M d t L 2 L1
Mi 0
F
F
M i 2r F 0
4

i
Fi 0 ,

i
物理学
三 质点的角动量定理
dp dt F
dL dt
？
5
物理学
d (r mv ) r mv dt dt dt dt dr dL dp v , v mv 0 r rF dt dt dt dL 质点角动量定理 M 的微分形式 dt
物理学
2.4 质点的角动量定理和角动量守恒定律
z
1. 质点的角动量 质量为 m 的质点以速 度 v 运动，某时相对 参考 点O 的位矢为 r ，则定义 质点对O的角动量为： L r p r mv 大小: L rm v sin 方向: 符合右手法则 角动量单位：kg· 2·-1 m s
O
z
F
r
d
*
P
M rF
d : 力臂
M
力矩的方向： （叉乘的方向）

07. 质点角动量与角动量守恒定律

07. 质点角动量与角动量守恒定律

mv2r2 mv1r1
v2r2 v1r1
表明小球对圆心的 角动量保持不变。
例：行星运动的开普勒第二定律。
解：太阳作为力心，行星受到有心引力， 万有引力，行星相对力心（太阳）的角动 量守恒。行星作平面运动，其轨道是以太 阳为焦点的椭圆。
0
r α
L mvr sin r r sin dr mr sin m lim t 0 dt t 2s m lim t 0 t ds 2m dt
显然，上关系中的Ｌ，Ｍ是相对同一参考 点而言。 类似质点的动量定理的讨论，有
dL Mdt
t2 L 2 L 2 Mdt t1
（冲量矩）
上关系用的不多，但基本概念应清楚。 如已知ｔ１～ｔ２的Ｌ变化，求平均力矩。
三、 角动量守恒定律 对某一参考点，若质点受的合外力矩为零， 则质点相对此点的角动量不变， Ｌ＝常矢 即质点相对此点的角动量守恒。 质点角动量守恒定律又表明了运动中存在 的一个不变量。 ∵Ｌ＝ｍｒ×ｖ 其方向也不变，决定了 质点在ｒ与ｖ确定的平面上运动。
§2－7 质点的角动量 角动量定理 一、力矩 角动量 力矩的定义：Ｍ＝ｒ×Ｆ
F M r 0 ｒＯ
α
Ｍ的大小：
Ｍ＝ｒＦｓｉｎα＝ｒ Ｆ ｒ ，力臂，０到力作用线的垂直距离。 Ｍ的方向： 右手螺旋法则。右手四指由ｒ向Ｆ方向 （小于π）转，拇指的方向，显然Ｍ垂直ｒ， Ｆ构成的平面。
Ｏ Ｏ
ＳＩ：ｍＮ（量纲同功，物理量不同。） 力矩的定义与力的三要素（力的大小、方 向、力作用点的位置（坐标）有关。）
ds/dt行星对太阳的位矢在单位时间扫过的面 积，掠面速度。 ∵Ｌ大小不变，ds/dt不变。
行星与太阳的连线在相同时间内扫过相等的面积

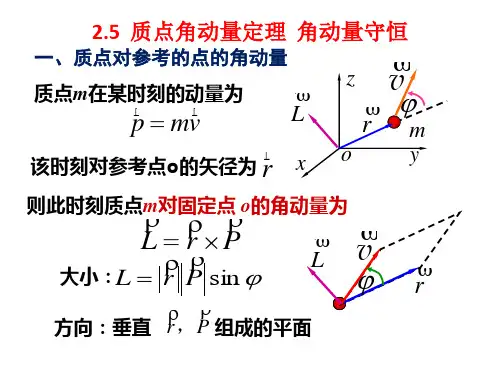
质点角动量定理 角动量守恒

质点角动量定理 角动量守恒

v2
o
v1
4)角动量守恒定律是物理学的基本定律之一。不 仅适用于宏观体系，也适用于微观系统。
2.5 质点角动量定理 角动量守恒
例1 一小球在光滑平面上作圆运动，小球被穿 过中心的线拉住 。开始时绳半径为r1 ，小球速 率为 v1 ；后来，往下拉绳子，使半径变为 r2 ， 小球速率变为 v2 ，求v2 =？
ri fi 0
i
有
dL M外 dt
质点系的角动量定理：质点系对某定点的角 动量的时间变化率等于质点系对该点的合外 力矩。
2.5 质点角动量定理 角动量守恒
结论：
1）内力对定点的力矩之和为零。 2）只有外力矩才能改变系统的总角动量。 3.质点系的对轴的角动量
L Lx i Ly j Lz k
当质点系对某点的合外力矩为零时，则质点 系对该点的角动量保持不变，称为角动量守恒定 律。
角动量守 恒例题
2.5 质点角动量定理 角动量守恒
盘状星系——角动量守恒的结果
质点系对o点的角动量
r2
o
r1
L Li ri Pi
i i
质点系对o点的角动量等于系统中各质点对 同一点角动量的矢量和。
2.5 质点角动量定理 角动量守恒
2.质点系的角动量定理
用 f i 表示第i个质点所受内力之和
用 Fi 表示第i个质点所受外力之和
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt d dt t
由速度定义
dr v v p 0 dt

质点系角动量守恒定律

质点系角动量守恒定律

dL τ ，再考虑诸质点所受惯性力的力矩，即得 dt
dL τ i外 ri (mi ac ) dt 式中惯性力矩又可写作 mi ri dL ( mi ri) ac ( ) mac τ i外 m dt
此即质点系对质心的角动量定理，与惯性系中角动量定理具有完 全相同的形式。是表明质心系特殊和重要性的又一个例子。
第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
当τ iz 0时,
Lz 常量.
§5.4 质点系对质心的角动量定理和 守 恒 定 律
前面给出的角动量定理和角动量守恒定律都相对于惯性系 而言，现在研究质心参考系中质点系角动量的变化规律。如图 （a），C xyz 即质心参考系。C 为质心，x ' , y ' 和 z 坐标轴
与惯性参考系 O xyz 的 x, y 和 z 轴总保持平行，而质心具有 加速度 ac 。 z
四、质点对轴的角动量定理和守恒定律（自阅）
§5.3 质点系的角动量定理及角动量守恒定 律
一、质点系角动量定理
设质点系由 N 个质点组成，对选定的某固定参考点，第 i 个 质 点的角动量定理的表达式为τ dLi

§4.4.1 质点角动量及其守恒定律

z
L
mv
m
(
kg· m2/s
)
o
x

大小：L rmv sin
r
y
方向：依右手定则
☻ L 不仅与质点的 v 有关, 且与原点o的选取有关 。
对圆运动，o点选在圆心。对有心力场的运动， o点
常选在力心上。
·4 ·
Chapter 4. 刚体
§4. 4 质点角动量及其守恒定律
积分形式：对同一参考点o，质点所受的冲量矩等于
·7 ·
Chapter 4. 刚体
§4. 4 质点角动量及其守恒定律
3. 质点角动量守恒定律
dL 若 M 0 ，即 M 0 ，则 L= 常矢量，质点 dt 的角动量守恒。
角动量守恒条件：
F
d 0F F 0
M r F 0
Chapter 4. 刚体
§4. 4 质点角动量及其守恒定律
§4.3 质点角动量及其守恒定律
·1 ·
Chapter 4. 刚体
§4. 4 质点角动量及其守恒定律
v
m
若 v 常数，则：
o
r
动量守恒吗？ p mv 常矢量 但 L r mv 常矢量
·2 ·

o
太阳
rB
B
rAv A rBvB rB rA vB v A
·10 ·
Chapter 4. 刚体
§4. 4 质点角动量及其守恒定律
水平台面上转动的小球角动量守恒
v
o
r F 0
F
rmv 常数
·11 ·
Chapter 4. 刚体

5-2 质点系的角动量定理及角动量守恒定律


若质点系的所有质点均分别在与 z 轴垂直的平 面内运动，且一共同的角速度绕 z 轴作圆周运动， 则质点系对 z 轴的角动量为
Lz ri mi vi mi ri
i i
2
当质点系对轴的角动量守恒时：
ri 变小，则
M z 0 ，Lz 常量
增大；
ri 变大，则
减小.
质点系对轴的角动量定理
质点系对轴的角动量定理
dLz Mz dt
如果在一个过程中，质点系所受的外力 对 z 轴的力矩始终保持为零，则质点系对该 轴的角动量守恒.
M z 0 ，Lz 常量
质点系对轴的角动量守恒定律
当内力矩远大于外力矩时，质点系对轴的角动量 也是守恒的. （例：P170例1）
在直角坐标系中，上式沿三个坐标轴的投影式为
dLy dLx dLz M x M ix , My , Mz . dt dt dt
• 如果只考虑上式中某一个分量，例如 z 分量，则 表现为对轴的特征：即质点系对于 z 轴的角动量对时 间的变化率等于质点系所受一切外力对 z 轴力矩的代 数和，叫做质点系对 z 轴的角动量定理。
ri fij rj f ji (ri rj ) fij 0
ri fij 0
i i j
成对出现的内力对参考点的力矩矢量和为零. 由于系统内力总是成对出现，则系统内力矩的矢量和为零. • 可见，系统的内力矩只能使系统内各质点的角动量改变， 但不能改变质点系总的角动量。
如果在一个过程中，始终无外力矩作用或所受 的外力矩为零，则质点系的总角动量守恒 .
M外 0 ，L 常矢量
质点系对某一固定点的角动量守恒定律

质点的角动量和角动量守恒

第三章运动的守恒定律§3-6 质点的角动量与角动量守恒定律1.角动量(Angular Momentum)rα定义：质点对点的角动量为Oαr()L r p r mv =⨯=⨯ 角动量大小（面积）αsin rmv L =LvLvm角动量方向O行星在公转轨道上的角动量ppϕϕrrd dpd L =ϕsin pr =（1）质点对点的角动量，不但与质点运动有关，且与参考点位置有关。

讨论（2）方向的确定LLαvrLαvrrαOmαrvL（3）做圆周运动时，由于，质点对圆心的角动量大小为v r⊥rmv L =L质点对圆心O 的角动量为恒量大小不变方向不变方向不变方向不变v角动量2. 角动量守恒定律(Conservation law of angular momentum)F1v 2v 2r 1r om1122r v r v =1122r mv r mv =表明小球对圆心的角动量保持不变实验中发现行星绕太阳的运动常量=pd 常矢量=⨯p r表明行星在运动过程中，对太阳的角动量保持不变。

Oppϕϕrrd dL r p=⨯对t 求导d d ()d d L r p t t =⨯ d d d d r pp r t t=⨯+⨯ 0)(d d ,d d =⨯=⨯=v m v p tr v t rF r tp r t L⨯=⨯=∴d d d d 质点的角动量守恒定律：如果作用在质点上的外力对某给定点O 的力矩为零，则质点对O 点的角动量在运动过程中保持不变。

这就叫做角动量守恒定律。

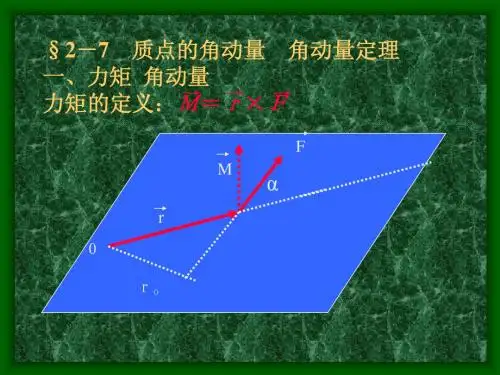
)(F r⨯角动量守恒定律力矩例题用角动量守恒定律证明开普勒第二定律。

解开普勒第二定律：任一行星和太阳之间的连线，在相等的时间间隔内扫过的面积相等。

O1v 1ϕ2ϕ2r 1r 2v 2d θ1d θ12课本例题3-14与之类似，自学。

11111()2θ=d d s r r 在位置1，d t 时间内，矢径转动的角度为，扫过的面积为1r1θd O1v1ϕ2ϕ2r 1r 2v 2d θ1d θ121111sin θϕ=d d r v t 由于所以11111111(sin )22ϕ==⨯d d d s r v t r v t 12=d L t m11111()2θ=d d s r r 在位置1，d t 时间内，矢径转动的角度为，扫过的面积为1r1θd O1v1ϕ2ϕ2r 1r 2v 2d θ1d θ12所以11111111(sin )22ϕ==⨯d d d s r v t r v t 12=d L t m两边都除以d t ，有O1v 1ϕ2ϕ2r 1r 2v2d θ1d θ12112=d d s L t m 11111()2θ=d d s r r 12=L m在位置1，d t 时间内，矢径转动的角度为，扫过的面积为1r1θd 两边都除以d t ，有在位置2，有O1v 1ϕ2ϕ2r 1r 2v2d θ1d θ12因为行星只受万有引力作用，所以相对于太阳的力矩为0。

质点的角动量



i
ri p i ,
对于标号为i的质点，它不仅受到来自系统外的作用力，而且 还受到系统内其它质点的作用力（内力）
fi

j
f ij ,
利用质点的角动量定理 可得
d dt
d Li dt
ri Fi f i ,

i


i
Li

i
ri ( Fi f i )
r1 , 以角速度 1旋转，然后慢慢向下拉 离为 r2时，拉力对质点所做的
v
绳，求质点离圆心距
功。

选小孔为参考点，任意 时刻质点受力矩 M r f 0 , 质点的角动量守恒，因 而有：
o r f
f
mr 1 1 mr 2 2
2 2
根据动能定理，外力做功为
v
O
rห้องสมุดไป่ตู้m
若一个质量为m的粒子在半径为r的圆周上以速 v 运动，则它的动量为 P m v ,相对于圆心的 度 位置矢量 r 与粒子运动速度 v 互相垂直 ，角 动量大小为： L m rv m r 2
是质点运动的角速度
角动量的方向由右手螺旋法则判断，垂直于物体转动 所在的平面
2
1
4、推广到质点系情形
利用牛顿第三定律，我们还可以将质点角动量定律推广到质 点系的情况，得到质点系总角动量的时间变化率与合外力 矩的简单关系，即质点系的角动量定理。 我们定义质点系对给定参考点O的总角动量为系统内所有质 点对选定参考点O的角动量的矢量和，即 ：
L

i
Li
多个外力作用于同一个质点的合力矩等于各 力的力矩的矢量和，即如果
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中，r代表的是从定点指
•
R
r
•
向质点的矢量，而非质点
的位矢 R。不过位移与坐
标系选取无关，所以有：
dR
dr
v
dt dt
2.4.4 质点角动量守恒定律
1. 质点角动量守恒定律
由质点角动量定理的微分形式可知，若 M 0 ，则：
L
r
p
常矢量
这叫质点角动量守恒定律。
2. 有心力作用下质点的运动 若质点始终受到一个指向固定点（称作力心）的作用力，
L
ri
pi
常矢量
i
这叫质点系角动量守恒定律。
必须指出：质点系所受合外力为零时，其角动量未必是守 恒的；反之，若质点系角动量守恒，也不意味着它所受合外 力为零。由此得到一个重要推论：质点系角动量守恒时，其 动量未必守恒；质点系动量守恒时，其角动量也未必守恒。
则称质点受有心力作用。例如，行星绕太阳的运动过程中， 太阳的万有引力就是有心力。
由于有心力始终通过力心，其力矩必然恒等于零，于是受 有心力作用的质点，对力心的角动量必守恒。
例2 — 17
L
r
v
m
L rm dr sin 2m dS 常量
dt
dt
dS 常量 dt
这便是开普勒行星第二运动定律。
2. 质点对定点的角动量
用质点的位置和动量，经过一个矢积运算，就可以构造出
质点对定点的角动量：
L
r
p
r
mv
L rmvsin ph
L
o• h
r
•
p
关于角动量的上述定义，同力矩的定义极为相似。
质点对定点的角动量，反映了质点绕着那个固定点的转动
情况。更几何化一点说，反映的是从定点到质点的那条连线
单位时间扫过的面积（面积速度）。 p
dr dr sin
O•
dS r ຫໍສະໝຸດ dS 1 r dr sin dS 1 r dr sin
2
dt 2 dt
L rm dr sin 2m dS
dt
dt
3. 圆周运动中的角动量 如果质点作圆周运动，则它对圆心的角动量大小为：
L mRv mR2
2.4.3 质点角动量定理
2.4 角动量及其守恒定律
2.4.1 力对定点的力矩
1. 影响物体转动状态的三个因素
•
•
•
分析表明，影响物体转动状态的因素有三个： （1）力的大小； （2）力的方向； （3）力的作用线到转轴的垂直距离（力臂）。
影响物体转动状态的三个因素其实可以用一个物理量来反 映，这就是我们将要介绍的力矩。
2. 力对定点的力矩
2.4.5 质点系角动量定理和角动量守恒定律
1. 质点系角动量定理
质点系对定点的角动量被定义为：
L
Li
ri pi
i
i
dL dt i
ri
dpi dt
i
ri
( Fi
f ji )
j i
容易证明，任何一对内力对同 一个定点的力矩矢量和为零：
ri f ji rj fij 0
ri
O•rj
fij
f ji
所以必有：
ri
f ji
0
i ji
于是质点系角动量定理的微分形式就成为：
dL
dt i
ri Fi
i
Mi M外
质点系角动量定理的积分形式如下：
t2
M外dt L2 L1
t1
2. 质点系角动量守恒定律
由质点系角动量定理的微分形式可知，若 M外 0 ，则：
1. 质点角动量定理的微分形式
dL
d
(r
mv )
r d (mv)
dr
mv
dt dt
dt dt
rF M
M
dL
dt
2. 质点角动量定理的积分形式
t2
Mdt L2 L1
t1
上式左边的积分叫冲量矩。
质点所受合力的冲量矩，等于质点角动量的增量，这叫 质点角动量定理。
有一点需要说明：在推导质点角动量定理微分形式的过程
定义力对定点的力矩：
M
M
r
F
o•
r
F
h
M M rF sin Fh
（1） （2）
M M
的方向垂直于 的大小等于由
F和 F和
rr决所定决的定平的行平四面边；形面积。
2.4.2 质点角动量
1. 对运动状态描述的补充 在质点运动学中我们已经知道，描述质点运动状态，只要
位置 r和动量 p（或速度）就足够了。但要描述质点系的运
动状态，只有位置和动量就不够了。请看下面的例子：
两个圆盘系统的总动量都为零，但它们明显地具有不同的 运动状态。我们必须有新的物理量来区分这两种状态才行。
用来区分上述两种不同状态的物理量叫角动量，也叫动量 矩。虽然从原则上说，描述质点运动状态完全可以不需要角 动量，但我们还是从定义质点角动量出发，然后再将其推广 到质点系（特别是后面要重点介绍的刚体系统）。