第52节质点系的角动量定理及角动量守恒定律
- 格式:pdf
- 大小:212.81 KB
- 文档页数:5




质点系的角动量定理质点系的角动量定理引言角动量是物理学中一个非常重要的概念,它描述了物体围绕某一轴旋转时所具有的特定性质。
在实际应用中,我们经常需要研究由多个质点组成的系统的角动量变化,这就涉及到了质点系的角动量定理。
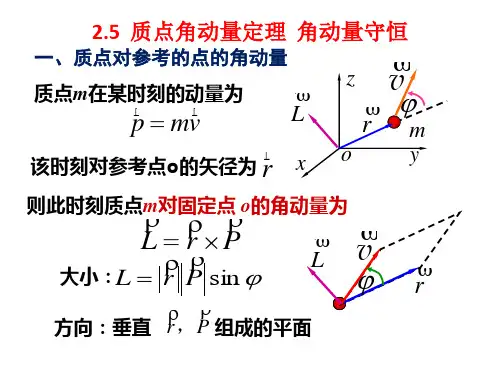
定义首先,我们来回顾一下单个质点的角动量定义:对于一个质量为m、速度为v、距离某一轴距离为r的质点,它的角动量L可以表示为L = mvr sinθ,其中θ是速度方向与轴线方向之间的夹角。
然后再考虑由N个质点组成的系统,每个质点都有自己的速度和位置。
此时,整个系统所具有的总角动量可以表示为L = Σi=1N L_i,即每个质点所具有的角动量之和。
推导接下来我们来推导一下质点系的角动量定理。
假设一个由N个质点组成的系统,在某一瞬间t1时刻它们所具有的总角动量为L1,在另一瞬间t2时刻它们所具有的总角动量为L2。
那么根据牛顿第二定律和牛顿运动定律,我们可以得到以下的式子:F = ma = m(dv/dt) = d(mv)/dt其中F是质点所受的合力,m是质量,v是速度。
将上式两边同时乘以r sinθ,再对所有质点的角动量求和,可以得到:Σi=1N (r_i x F_i) = d/dt (Σi=1N L_i)其中r_i是第i个质点距离某一轴的距离向量,F_i是它所受的合力向量。
右边表示总角动量随时间的变化率。
根据矢量积的性质,r_i x F_i可以表示为m_iv_ir_isinθ_i,其中θ_i是速度方向与轴线方向之间的夹角。
将其代入上式中可得:Σi=1N m_iv_ir_isinθ_i = d/dt (Σi=1N L_i)这就是质点系的角动量定理。
应用利用质点系的角动量定理,我们可以研究各种旋转系统中角动量随时间变化的规律。
例如,在自由陀螺运动中,陀螺在自身重力作用下绕着固定轴线旋转。
由于陀螺具有一定的自旋角速度,它的角动量会随时间变化。
根据质点系的角动量定理,我们可以推导出陀螺的进动和章动规律。




质点系的角动量定理介绍质点系的角动量定理是力学中的一项基本原理,用于描述质点系在外力作用下角动量的变化规律。
本文将全面、详细、完整地探讨质点系的角动量定理。
角动量的定义角动量是描述物体旋转状态的物理量,表示物体围绕某一轴旋转时具有的转动能力。
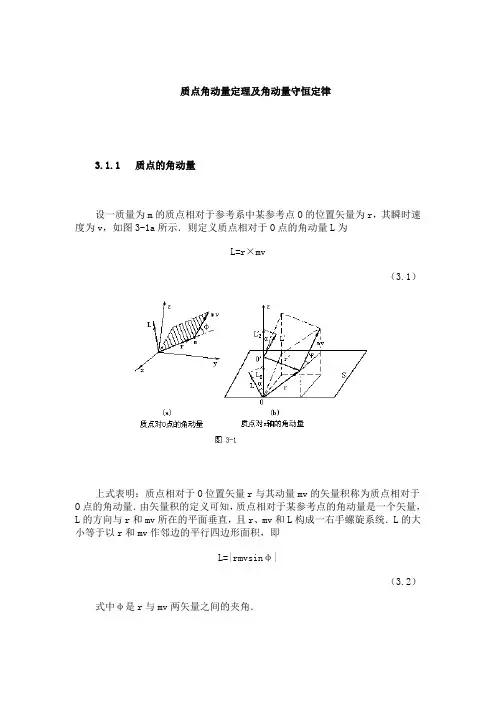
对于一个质点,其角动量可以定义为质点的质量乘以质点的位置矢量与旋转轴之间的叉乘。
角动量的数学表达式为:L=r×p其中,L表示角动量,r表示质点相对于某一轴的位置矢量,p表示质点的动量。
角动量定理的表述质点系的角动量定理可以表示为:dLdt=M其中,dLdt表示角动量的变化率,M表示作用在质点系上的合外力矩。
角动量定理的推导为了推导角动量定理,我们需要使用牛顿第二定律和角动量的定义。
考虑一个质点系,由n个质点组成。
对于其中的第i个质点,根据牛顿第二定律,可以得到:m i d2r idt2=F i其中,m i表示第i个质点的质量,r i表示第i个质点的位置矢量,F i表示作用在第i个质点上的合外力。
将角动量的定义代入上式可得:m i d 2r i dt 2=d dt (r i ×m i dr i dt) 对上式进行展开和简化可以得到:m i d 2r i dt 2=m i dr i dt ×dr i dt +r i ×m i d 2r i dt 2 根据向量恒等式A ×(B ×C )=B (A ⋅C )−C (A ⋅B ),可以得到:m i d 2r i dt 2−r i ×m i d 2r i dt 2=m i dr i dt ×dr i dt将上式对所有质点求和,并利用质点系的总动量定义p =∑m in i=1dr i dt 和质点系的质心位置矢量定义R =1M ∑m i n i=1r i (其中M =∑m i n i=1),可以得到:dp dt=F −R ×F 其中,F 表示质点系的合外力。
质点系统的角动量角动量是物体旋转时所具有的性质,质点系统的角动量是由其中所有质点的角动量之和组成的。
质点系统的角动量具有许多重要的特性和应用,如守恒定律和撞击问题。
本文将探讨质点系统的角动量及其相关概念和应用。
一、质点系统的角动量定义质点系统的角动量是由其中每个质点的质量、速度和与某一旋转轴的距离共同决定的。
对于一个质量为m的质点,其角动量可以用以下公式表示:L = m * r * v * sinθ其中L表示角动量,m表示质点的质量,v表示质点的速度,r表示质点与旋转轴的距离,θ表示速度方向和质点距离旋转轴的夹角。
二、质点系统的角动量守恒定律质点系统的角动量守恒定律是指在没有外力和外力矩作用下,质点系统的总角动量保持不变。
这意味着在系统内部发生作用时,质点系统整体的角动量不会改变。
例如,考虑一个由两个质点组成的系统,当两个质点之间的距离发生变化时,一个质点靠近旋转轴,另一个质点离开旋转轴。
质点的速度会相应改变,但是质点系统的总角动量保持不变。
三、质点系统的角动量守恒的应用质点系统的角动量守恒定律在解决撞击问题时发挥了重要的作用。
当两个物体发生碰撞时,守恒定律可用于计算碰撞前后物体的角动量变化。
考虑一个由两个质点组成的系统,在碰撞前,两个质点的角动量分别为L1和L2。
碰撞发生后,两个质点的角动量分别为L1'和L2'。
根据角动量守恒定律,可以得到:L1 + L2 = L1' + L2'通过对碰撞前后质点的速度和质量进行分析,可以解出碰撞后质点的速度和角动量变化。
四、实际示例:自行车轮转动中的角动量进一步说明质点系统的角动量,我们可以以自行车轮的转动为例。
当自行车轮旋转时,每个质点在轮辐上的角动量会以一定的方式组合成轮子整体的角动量。
当骑行者使自行车轮旋转速度加快时,轮子的角动量也将相应增加。
这可以通过调整骑行者身体的位置来实现。
如果骑行者将身体朝轮子的一个方向倾斜,轮子会产生相反方向的反作用力,从而改变了质点系统的角动量。