当前位置：文档之家 › 质点系角动量定理

质点系角动量定理

  • 格式：ppt
  • 大小：398.50 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

角动量定理.pdf

角动量定理.pdf

A M r o
x2
m
解：在地面参考系中， 在地面参考系中，建立如图 x 坐 标，设滑轮半径为 r 有： B
l = AA′ + AB + BB′ = x1 + x2 + πr
B′
s
s = x1 − x 2
mAA′ m = ⋅ x1 , l
mAB
m = ⋅ πr l
m = ⋅ x2 , l
A′
x1
x
mBB′
µ
m2
ro m
m1
m2 和滑轮为研究对 解：在地面参考系中， 在地面参考系中，选取 m1 、 象，分别运用牛顿定律 分别运用牛顿定律和 牛顿定律和刚体定轴转动定律得 刚体定轴转动定律得：
T1
N
aT2T2o向里+Ny
m1
a
m1 g
µm2 g
m2
m2 g
Nx
T1
列方程如下： 列方程如下：
m 1 g − T1 = m 1 a T2 − µ m 2 g = m 2 a 1 2 T1 r − T 2 r = m r β 2 a = rβ
用隔离法列方程: (以逆时针方向为正) A M r o
CA x2 x1
m
T1
T2 CB . m Bg T1
B
CB
. CA
m Ag
Jr T2
B′
s
A′
m A g − T1 = m A a
x
T2 − mB g = mB a
T1r − T2 r = Jβ 2 2 J = J M + J AB = 1 Mr + m r AB 2
T1
r a1
以向下为正方向

质点系角动量守恒定律

质点系角动量守恒定律

dL τ ，再考虑诸质点所受惯性力的力矩，即得 dt
dL τ i外 ri (mi ac ) dt 式中惯性力矩又可写作 mi ri dL ( mi ri) ac ( ) mac τ i外 m dt
此即质点系对质心的角动量定理，与惯性系中角动量定理具有完 全相同的形式。是表明质心系特殊和重要性的又一个例子。
第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
当τ iz 0时,
Lz 常量.
§5.4 质点系对质心的角动量定理和 守 恒 定 律
前面给出的角动量定理和角动量守恒定律都相对于惯性系 而言，现在研究质心参考系中质点系角动量的变化规律。如图 （a），C xyz 即质心参考系。C 为质心，x ' , y ' 和 z 坐标轴
与惯性参考系 O xyz 的 x, y 和 z 轴总保持平行，而质心具有 加速度 ac 。 z
四、质点对轴的角动量定理和守恒定律（自阅）
§5.3 质点系的角动量定理及角动量守恒定 律
一、质点系角动量定理
设质点系由 N 个质点组成，对选定的某固定参考点，第 i 个 质 点的角动量定理的表达式为τ dLi

2-7 角动量定理 角动量守恒

2-7 角动量定理 角动量守恒
方向

10
三、质点的角动量定理和角动量守恒定理 由 L r p dr d p dL d 有： pr ( r p) dt dt dt dt
v mv r F r F M
11
于是有 或
与固定点有关 与内力矩无关 守恒条件 ri Fi 0
i
25
书59、72页例2-9、16
V0
解: 应用角动量定理
C
B
A
Rm Av0 RmB v0 Rm Av RmB v Rmc v
V0
m A mB mC
2 v v0 3
26
mB m A v B v A ,同时到达
21
例：重解上节例题
解： M：
m：
M合
M合
r T RT
r T RT
h m
m M
M外 0
角动量守恒
v
初始 m M 末时 m
L
m 2ghR
T mg , Mg
2gh
0
m 2gh mv Mv

（中心力）
v
· F r
O

（1） mv r sin =const.， （2）轨道在同一平面内。
13
若 M z 0 ，则 Lz 常量 — 质点对轴的角
动量守恒定律
角动量守恒定律是物理学的基本定律之一， 它不仅适用于宏观体系， 也适用于微观体系， 而且在高速低速范围均适用。
14
例
用角动量守恒定律导出开普勒第二定律 -- 行星单位时间内扫过的面积相等。 O
F引 F向 ， r 就不变了，

质点的角动量定理公式

质点的角动量定理公式

质点的角动量定理公式
质点角动量定理是物理学的一条基本定理，它是由古老的天文学家兼物理学家们在18世纪早期发现的，它说明一个质点的角动量不可能有一个变化。

这条定理一直在物理学中有着重要意义。

它能够解释角动量在物理系统中的变化，以及系统中的角动量保持不变。

质点角动量定理的公式可以用来计算系统的角动量和内部总力的总和。

该公式的表达为：L = Iα + F(r)，其中L表示系统的角动量，Iα表示从力学角动量，而F(r)则是由外部力（或作用）所产生的角动量。

因此，角动量定理可以被用来解释角动量如何在物理学中变化。

它可以让我们看到影响角动量变化的力，也在物理计算中得到应用。

例如，当一个小物体在外力的作用下旋转时，我们可以用它来计算准确的角度变化。

还可以用它来研究外力的效应的大小，以及它们可能影响到系统的初始角动量。

总之，质点角动量定理是一条重要的定理，它可以提供有关角动量变化原理的信息，在物理学中有着重要意义。

它对于研究和理解外力对角动量变化的影响具有重要作用，也能被用于物理学计算中。

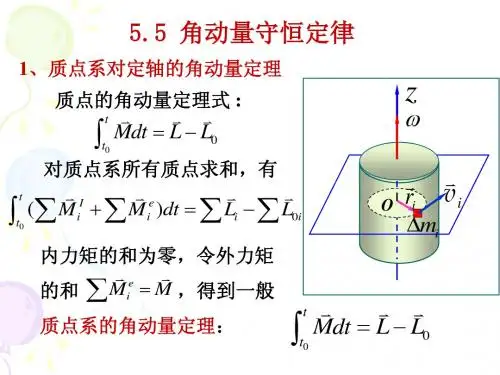
5.5 角动量守恒定律

5.5 角动量守恒定律

例题1 ： 一粒子弹水平射入一静止悬杆的下端，穿出 后速度损失 3 / 4，求子弹穿出后棒的角速度 。已知轴处自由 。
解：以 f 代表杆对子弹的阻力，对子弹有: fdt m(v v0 ) 3mv0 / 4
子弹对杆的冲量矩为：

l f dt J f ldt
若 M 0 ，则
L J 常量
——刚体定轴转动的角动量守恒定律
讨论
内力矩不改变系统的角动量.
在冲击等问题中
M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律. 刚体（或刚体组系统）角动量守恒的三种情况： ①J 不变（刚体），角速度ω的大小和方向均不变 ②J 可变（质点系），ω亦可变，但Jω乘积不变 ③刚体组的角动量守恒
a
v
m
3mva 2 2 m' l 3ma
射入竿后，以子弹、细杆和 地球为系统 ，机械能守恒 .
o
30
a
1 1 2 2 2 ( ml ma ) 2 3 l mga(1 cos 30) mg (1 cos 30) 2
2 2 v g (2 3 )( m l 2ma )( m l 3ma ) 6 ma
质点系的角动量定理：

t
t0
Mdt L L0
质点系的角动量定理：

t
t0
Mdt L L0
O

ri
mi
z
该矢量式向固定转轴（如 z轴） 的投影，得一个标量式，即
vi

t
t0
M z dt Lz L0 z
相对某固定轴，质点系所受的角冲量等于系统 角动量的增量。——质点系对定轴的角动量定理。

质点系角动量定理

质点系角动量定理

质点系角动量定理
质点系的角动量定理有多种形式。

设质点系中第i个质点的质量为m i，位矢为r i，速度为，受的外力为F i，则对静点（惯性系的原点）的角动量定理为
(1)
这是基本形式。

还有对质心的角动量定理：
(2)
其中为质点i相对于质心C的位矢和速度。

质心是动点，但很特殊，因为它是系统的（以质量为权的）平均位置，或者说是质量空间位置分布的一阶原点矩。

式(2)右边的“对质心的角动量”可以视为某种二阶中心矩（如果其中的速度换为矢径的话）。

如果对其他动点P，角动量定理就没这么简单，会多出一项：
(3)
其中为质点i相对于动点P的位矢和速度，而r CP 为质心相对于P点的位矢。

这里多出来的一项是由于动点具有加速度，故而换到非惯性系中时各质点还受到惯性力。

正是这些惯性力力矩之和。

如果动点就是质心，那么r CP=0，惯性力力矩之和为0，式(3)右边第二项就不存在。

对于刚体情形，以上各定理都有更为具体形式，不赘述。

但此时还有一个对瞬心的角动量定理（或转动定律）。

文献[1]从刚体绕瞬心的动能定理
(4)
（P为瞬心，M P为刚体受到的绕瞬心的力矩，I P为刚体绕瞬心的转动惯量，ω为刚体的角速度）出发，得到刚体绕瞬心的转动定律（角动量定理）：。

5-2 质点系的角动量定理及角动量守恒定律


若质点系的所有质点均分别在与 z 轴垂直的平 面内运动，且一共同的角速度绕 z 轴作圆周运动， 则质点系对 z 轴的角动量为
Lz ri mi vi mi ri
i i
2
当质点系对轴的角动量守恒时：
ri 变小，则
M z 0 ，Lz 常量
增大；
ri 变大，则
减小.
质点系对轴的角动量定理
质点系对轴的角动量定理
dLz Mz dt
如果在一个过程中，质点系所受的外力 对 z 轴的力矩始终保持为零，则质点系对该 轴的角动量守恒.
M z 0 ，Lz 常量
质点系对轴的角动量守恒定律
当内力矩远大于外力矩时，质点系对轴的角动量 也是守恒的. （例：P170例1）
在直角坐标系中，上式沿三个坐标轴的投影式为
dLy dLx dLz M x M ix , My , Mz . dt dt dt
• 如果只考虑上式中某一个分量，例如 z 分量，则 表现为对轴的特征：即质点系对于 z 轴的角动量对时 间的变化率等于质点系所受一切外力对 z 轴力矩的代 数和，叫做质点系对 z 轴的角动量定理。
ri fij rj f ji (ri rj ) fij 0
ri fij 0
i i j
成对出现的内力对参考点的力矩矢量和为零. 由于系统内力总是成对出现，则系统内力矩的矢量和为零. • 可见，系统的内力矩只能使系统内各质点的角动量改变， 但不能改变质点系总的角动量。
如果在一个过程中，始终无外力矩作用或所受 的外力矩为零，则质点系的总角动量守恒 .
M外 0 ，L 常矢量
质点系对某一固定点的角动量守恒定律

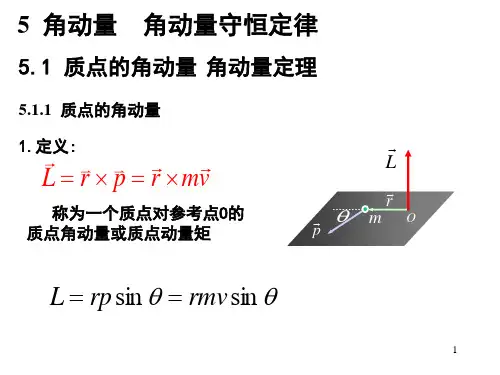
第5章角动量角动量守恒定律

任一行星和太阳之间的联线,在相等 的时间内扫过的面积相等, 即掠面速 度不变.
(2) 说明天体系统的旋转盘状结构.
v
r
O
B S
A r
[证明]
(1) 行星对太阳O的角动量的大小为 L r p rmvsin
其中 是径矢 r 与行星的动量 p 或速度 v 之间的夹角.
用 s 表示 t 时间内行星所走过的弧长, 则有
dt
若 M外 0
则 dL 0 或 L 常矢量
dt
若对某一固定点，质点所受合外力矩为零， 则质点对
该固定点的角动量矢量保持不变。
例：质点做匀速直线运动中，对0点 角动量是否守恒？
Lo r mv
rmvsin
r mv
L
r
O r
A
p mv
6
例 试利用角动量守恒定律:
1) 证明关于行星运动的开普勒定律:
v1
r1
B S
A
O
r1
积, 如图中所示.
其中 d /dt 称为掠面速度.
由于万有引力是有心力, 它对力心O的力矩总是等于零, 所以角动量守恒, L=常量, 行星作平面运动, 而且
d L 常量
dt 2m
这就证明了掠面速度不变, 也就是开普勒第二定律.
8
(2) 角动量守恒说明天体系统的旋转盘状结构
lim L r ms sin
t0 t
lim L
2m 2m d
t0 t
dt
若用 r 表示从O到速度矢量 v 的垂直距离, 则有
r sin s rs 2
7
lim L
2m 2m d
t0 t
dt
C D
其中 是 t时间内行星 v2

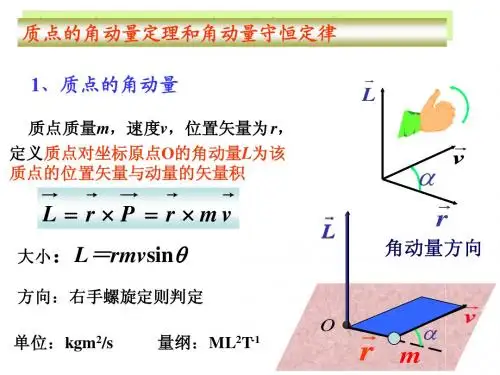
质点的角动量



i
ri p i ,
对于标号为i的质点，它不仅受到来自系统外的作用力，而且 还受到系统内其它质点的作用力（内力）
fi

j
f ij ,
利用质点的角动量定理 可得
d dt
d Li dt
ri Fi f i ,

i


i
Li

i
ri ( Fi f i )
r1 , 以角速度 1旋转，然后慢慢向下拉 离为 r2时，拉力对质点所做的
v
绳，求质点离圆心距
功。

选小孔为参考点，任意 时刻质点受力矩 M r f 0 , 质点的角动量守恒，因 而有：
o r f
f
mr 1 1 mr 2 2
2 2
根据动能定理，外力做功为
v
O
rห้องสมุดไป่ตู้m
若一个质量为m的粒子在半径为r的圆周上以速 v 运动，则它的动量为 P m v ,相对于圆心的 度 位置矢量 r 与粒子运动速度 v 互相垂直 ，角 动量大小为： L m rv m r 2
是质点运动的角速度
角动量的方向由右手螺旋法则判断，垂直于物体转动 所在的平面
2
1
4、推广到质点系情形
利用牛顿第三定律，我们还可以将质点角动量定律推广到质 点系的情况，得到质点系总角动量的时间变化率与合外力 矩的简单关系，即质点系的角动量定理。 我们定义质点系对给定参考点O的总角动量为系统内所有质 点对选定参考点O的角动量的矢量和，即 ：
L

i
Li
多个外力作用于同一个质点的合力矩等于各 力的力矩的矢量和，即如果

5--角动量 角动量守恒定律x


t=0
刚体定轴转动
ω ω
v
v
4. 线量与角量关系
dS = r ⋅ dθ
பைடு நூலகம்r a
切向分量 法向分量
dv dω at = = r = rα dt dt v2 an = = rω2 r
匀变速定轴转动
v v v v =ω×r
z
ω
v
20
r
O
dS
dθ P
匀变速直线运动
dS v= dt dv a= dt
v = v0 + at 1 2 S = v0t + at 2 2 v2 − v0 = 2aS
一对内力的力矩互相抵消 一对内力的力矩互相抵消 力矩
v v v v dL 量 M外 = 0时 = 0 L = ∑Li = 常 dt v M外 = 0 讨论; 不要求系统孤立, 讨论 1) 不要求系统孤立 只要求 v 2) 矢量式有 个分量式 即 M 的某个分量 矢量式有3个分量式 个分量式,即 的某个分量=0, 则相应角 外
v m ri i
∑
∑
角动量守恒说明天体系统的旋转盘状结构
12
猫尾巴的功能
已知：轻绳， 忽略滑轮的质量和轴的摩擦) 已知：轻绳，v10 = v20 =0，(忽略滑轮的质量和轴的摩擦) 问：m1= m2时，(A) m1先到；(B) m2先到；(C) 同时到 先到； 先到；
m1≠ m2时，(A) m1先到；(B) m2先到；(C) 同时到 若m1< m2 先到； 先到；
由角动量定理
r N
以向纸 内为正
O R
M外
dL r (爬) (不爬 mg 不爬) r 不爬 若 m1 > m2 : < 0, ∴ L < 0 m2g 爬 1 dt 轻的升得快； 有 m1v1 − m2 v2 < 0, ∴ v1 < v2 轻的升得快；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
L mvd k
由上例可以看出，并非质点仅在圆周运动时才具有角动量， 质点作直线运动时，对于不在此直线上的参考点也具有角动量。
另外，还可以看出，如果把参考点选在该直线上，则sin 0，
质点对该点的角动量永远等于零。因此，当谈到角动量时，必 须指明是对哪个参考点而言的，否则没有意义。
二、力对一参考点的力矩
轴线的一个分量，下面将给出力矩的一般定义。
如右图所示，O 是空间一点，F 是作
z
F
用力，A 表示受力点，受力点相对于 τ 参考点O 的位置矢量 r 与力 F 矢量的
φ
矢量积τ 叫做力 F 对参考点O的矩，
rA
其数学表达式为τ= r× F
xO
y
由定义可知，同一个力对于不同的参考点有不同的力矩，
因此讲到力矩时必须指明是相对哪一点而言的。当力 F不为零 时，力矩τ仍可能为零，这有两种情况：一是力的作用点就在参 考点 O ，此时位置矢量 r =0；另一种是沿力的方向的延长线通
L
于参考点的位置，故又与参考点的
φ
选择有关。例如，图（b）中对 o点
r
的角动量与对 o点角动量是不相同
O
y
的。
x
（a）
z
Lz L
o r mv s
L Lz r
o （b）
应当指出的是，虽然质点相 对于任一直线（例如 z 轴） 上的不同参考点的角动量是
不相等的，但是这些角动量
在该直线上的投影却是相等 的。如图（b）所示，取 S 平
三、质点对参考点的角动量定理和守恒定律
1
rv
常量
dt
dt
dt
2
因在平面内运动，故 r v 恒矢量 2
● 橡皮筋实验，掠面速度亦为一恒量
● 量）上质，述点能不匀否同速对的直它运线们动运提有动供共，统同对一特线的征外动，任力即一学点描r 掠述v2面？速恒度矢守量恒，（运动学
前两种运动的动量、动能均发生变化， 后一种动量、动能 均守恒。因此，动量和动能都不是对上面现象作出统一描述的
影面积，两者是相同的，故 Lz Lz 上述三个典型例子意味着对选定的参考点的角动量守恒。
我们把质点对 z 轴上任一点的角动量 L 在 z 轴上的投影，叫
做质点对于 z 轴的角动量，用 Lz表示，上面已证明， Lz的数值是
与参考点无关的。
y
[例题] 质量为 m 的质点在 xy
m v
平面内以速度 v 作匀速直线运动，
物理量。研究上述问题总需要选择参考点，对于一矢量，常可 研究它对某参考点的“矩”。 定义：质点对于参考点的位置矢量与其动量的矢积
L r mv r p 称为质点对该参考点的角动量（或
动量矩）。
此时它包含了质量，是一个动力学量！
z
L 含有动量 mv 因子，因此与参考
mv
系有关；L 还含有 r 因子，r 又依赖
过参考点 O ，此时sinφ=0 。如果质点在运动中受到的力始终 指向某个固定的中心，这种力叫做有心力，该固定点称为力
心，上述第二种情况，有心力相对于力心的力矩恒为零。
力对 O 点的力矩τ 在通过 O 点的任一轴线如 z 轴上的分量， 叫做力对轴线 z 的力矩，用 τz 表示，这就是中学物理课中给出 的力矩的定义。正如上面对于角动量的讨论一样，力 F对于轴 线 z 上任一点的力矩τ 在该轴线上的分量的数值 τz 是与所选参 考点无关的。
前言
一、本章的基本内容及研究思路
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角
面与 z 轴垂直，则质点对于o
点及 o点的角动量分别为 L
与 L ，L 和 L 分别等于以 r 及mv 为邻边及以 r及mv为邻边的平 行四边形的面积，L 与 L 在 z 轴上的投影分别是 Lz L cos
和 Lz Lcos(与分别是L与L和z轴间的夹角) ，由图 （b）可见，L 和 L分别是相应的两个平行四边形在 S 面上的投
普遍的定律之一。由于角动量这个物理量，从概念到数学表达， 都比动量要难理解，我们循序渐进逐步深入地来理解。
本章还要触及对称性的概念，尽管经典力学中的对称性没 有在微观领域中那么重要，但是介绍一下与本课水平相当 的对称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义； 2. 掌握质点、质点系的角动量定理； 3. 掌握角动量守恒定律； 4. 理解对称性的概念，了解守恒律与对称性的关系。
O
如图所示，求此质点相对于原点 O 的角动量。
d
r
[解] 根据角动量的定义式 L r mv, O
x
设 k 为沿 z 轴的单位矢量，则质点的角动量为
L r mv rmv sin k 即 L 指向 z 轴负方向。由上图可以看出，r sin 正好等于 O 点
与轨道的垂直距离 d ，因此代入上式得
动量及其规律很容易说明。特别是在有些过程中动量和机械能 都不守恒，却遵从角动量守恒定律，这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态，在近代物理理 论中仍然是表征微观运动状态的重要物理量，例如原子核的角 动量，通常称为原子核的自旋，就是描写原子核特性的。
角动量守恒定律和动量守恒定律一样，是自然界最基本最
三、本章的思考题及练习题
1. 思考题：教材P175，
2. 练习题：5.1.2 5.1.3 5.1.7 5.1.8 5.1.9 5.2.2
§1 质点的角动量
一、质点的角动量
角动量的概念是怎么引出来的？三个重要的例子（教材第 149页）
● 行星绕太阳公转时，掠面速度守恒
ds
1 r dr 2

1 r vdt 2
动量定理说明，引起动量改变的原因是力；下面将看到， 引起角动量改变的原因是力矩。
对于力矩的概念，虽然在中学物理课中已作过初步介绍，
例如，推门时作用力对门轴有力矩，用扳手拧螺帽时作用力对
螺杆的轴有力矩等，但那里讨论的只是物体绕一定轴线转动，
所遇到的力矩总是对轴的力矩，是力矩的一种特殊形式，力矩
的普遍定义是对一定参考点的，对轴的力矩只是对点的力矩沿