由质点系的角动量定理得刚体绕定轴转动的角动量定理

解： 设轴反力为 Nx，Ny。
由转动定律： 由质心运动定律：
O c
得： 讨论： 当 l =2l/3 时， Nx =0 。 l > 2l/3 时，Nx >0 ，l < 2l/3 时， Nx <0 。
[例] 半径为 R1 和 R2、转动惯量为 J1 和 J2 的两个圆柱 体，可绕垂直轴转动，最初大圆柱体的角速度为 0，现将 小圆柱体靠近碰到大圆柱体。由于摩擦，小圆柱体被带着 转动，当相对滑动停止时，两圆柱体各以恒定角速度沿相 反方向转动。求小圆柱的最终角速度多大？
M
m
[例] 一质量为m ，长为 l 的均质细杆，转轴在O点，距A 端 l/3 。今使棒从静止开始由水平位置绕O点转动，求(1) 水平位置的角速度和角加速度。(2)垂直位置时的角速度 和角加速度。 c B A 解： O
(1) 方向：
(2)
A
c
Bபைடு நூலகம்
O

[例] 一半径为R，质量为m的均匀圆盘平放在粗糙的水 平面上。若它的初角速度为0，绕中心o旋转，问经过 多长时间圆盘才停止？（设摩擦系数为）
x
转动平面
2. 刚体的角速度 角加速度
角速度
的方向：
角加速度的方向： 加速转动时，两者同方向，减速转动时，两者反方向。
3. 线量与角量的关系：
j
r
匀角加（减）速转动：
匀加(减)速直线平动：
式中：
是 t =0 时刻的角速度和角位置。
说明：作定轴转动时，刚体内各点具有相同的角量， 但不同位置的质点具有不同的线量。
1
2 得：
[例] 均质细棒：m1、 l ，水平轴O，小球：m2与棒 相碰，碰前 碰后 如图，设碰撞时间很短，棒保 持竖直，求碰后棒的角速度。 O 解： 系统对O轴角动量守恒

第五章 角动量•关于对称性
前言 质点的角动量 质点系的角动量定理及角动量守恒定律 质点系对质心的角动量定理和守恒定律 对称性 • 对称性与守恒律 经典动力学的适用范围
§5.1 前
一、本章的基本内容及研究思路
言
角动量概念的建立和转动有密切联系，在研究物体的运动 时，人们经常可以遇到质点或质点系绕某一确定点或轴线运动 的情况，并且在这类运动中也存在着某些共同的重要规律。例 如，天文观测表明，行星绕日运动遵从开普勒第二定律，在近 日点附近绕行速度较快，远日点速度较慢，这个特点如果用角 动量及其规律很容易说明。特别是在有些过程中动量和机械能
都不守恒，却遵从角动量守恒定律，这就为求解这类运动问题 开辟了新途径。
角动量不但能描述经典力学中的运动状态，在近代物理理 论中仍然是表征微观运动状态的重要物理量，例如原子核的角 动量，通常称为原子核的自旋，就是描写原子核特性的。 角动量守恒定律和动量守恒定律一样，是自然界最基本最
普遍的定律之一。由于角动量这个物理量，从概念到数学表达，
都比动量要难理解，我们循序渐进逐步深入地来理解。 本章还要触及对称性的概念，尽管经典力学中的对称性没
有在微观领域中那么重要，但是介绍一下与本课水平相当的对
称性问题是十分有益的。
二、本章的基本要求
1. 理解质点及质点系角动量的物理意义； 2. 掌握质点、质点系的角动量定理； 3. 掌握角动量守恒定律； 4. 理解对称性的概念，了解守恒律与对称性的关系。
由上（1）式可以看出，在过程中如果外力对参考点的力矩
的矢量和始终为零，则质点系对该点的角动量保持不变，称为 质点系对该点的角动量守恒定律，即
当τi 0时,
L 常量.
由（2）式可以看出，有时外力矩对参考点虽不为零，但 是，外力矩沿某固定的 z 轴分量为零，则质点系对 z 轴的角动 量保持不变，叫做质点系对 z 轴的角动量守恒定律。即

或 Lz = I = 恒量
当刚体相对惯性系中某给定转轴的合外力矩为 零时，该刚体对同一转轴的角动量保持不变。
——对转轴的角动量守恒定律
二、定轴转动中的角动量守恒
说明 1、 关于该守恒定律的条件：
Mz Miz 0
特别地，若每一个力的力矩均为零，即 则
二、定轴转动中的角动量守恒
M iz ri Fi sini 0 的几种情况
10
f
20
O1 R1 A
R2 O2 fB
随堂练习
当两圆柱接触处无相对滑动时，两者转速相反
10
20
O1 R1 A
R2 O2 B
且两者接触点的线速率相等！
二、定轴转动中的角动量守恒
由定轴转动的角动量定理
Mz
dLz dt
若刚体所受对转轴的合外力矩 M z 0，则有
dLz d ( I ) 0
dt
dt
二、定轴转动中的角动量守恒
(3) 对共轴非刚体系（其中各质元到转轴的距离可 变则）系：统的转动惯量可变，此时系统对转轴的角动量守恒，
即：I =恒量
• 特别地，若各质元的 保持一致，
Lz =I =恒量
当 I 增大时， 就减小； 当 I 减小时， 就增大 。
二、定轴转动中的角动量守恒
例如：花样滑冰运动员在冰面上旋转时 运动了角动量守恒定律
（1）
（2）
（3）
二、定轴转动中的角动量守恒
2、对转轴的角动量守恒定律的适用范围： • 不仅适用于刚体， • 也适用于绕同一转轴转动的任意质点系。
二、定轴转动中的角动量守恒
3、对转轴的角动量守恒的几种典型表现 (1) 对定轴刚体：I 不变， 大小和方向均不变；

这个例子表明，对于一个运动质点，在指定参考 系中，相对不同的固定参考点，有不同的角动量。质 点动量的方向不指向参考点时，它具有绕定点转动的 倾向，角动量不为零。如果质点作惯性运动 ( M 0) ， 质点角动量是守恒量。 [例题2] 质点 m 在 z 0平面内以速率 v 绕原点O逆时 针匀速转动。圆周轨道半径为 r ，求它相对于原点O 的角动量。 l 解：质点的动量矢量随时 变化，但它相对于原点O o r 的角动量却是个常矢量。 m v
立即得到
dl M dt
——称为质点的角动量定理
式中 M r F 是合外力相对惯性系中固定参考 点的力矩。
l r mv 是质点 m 相对于同一参考点的角
动量 。
表明相对于同一参考点，质点受到的合(外)力 矩等于质点角动量的时间变化率。
这个定理把质点所受的合外力矩和它角动量的瞬 时变化率联系起来了。 显然，若 M 0 则
r
m
F
在小球与 O点距离缩短的过程中，轨道是缓慢 收缩的螺旋线，径向拉力并不垂直于轨道切线， 正是拉力的切向分量使小球有切向加速度，速率 增加。
小球动能变化
Ek Ek 0 1 2 1 2 1 2 r02 mv mv0 mv0 ( 2 1) 2 2 2 r
小球轨道半径由 r0收缩到 r的过程中，拉力 F 所作的功
i
注意：外力矩与参考点的选择有关。
二、
系统内力性质的小结
⑴ 内力成对出现，所有内力的矢量和为零。 ⑵ 一对内力的功与参考系的选择无关，一对保守 内力的功还与路径无关且等于系统相关势能的减少， 非保守内力的功是系统机械能和其它形式能量转换 的量度。 ⑶ 在任一过程中，所有内力冲量的矢量和为零。 ⑷ 内力不影响系统质心的运动状态，不改变系统 的总动量。内力的冲量使总动量在系统内部重新分 配。 ⑸ 系统内力相对任一固定参考点的力矩矢量和 为零，内力矩不改变系统的总角动量。

典型例子
[例题]如图(a)表示半径为R的放水弧形闸门，可绕图中
左方质点转动，总质量为m,质心在距转轴
7 9
2 处，闸 R 3
门及钢架对质点的总转动惯量为 I mR 2 ,可用钢丝 绳将弧形闸门提起放水，近似认为在开始提升时钢架 部分处于水平，弧形部分的切向加速度为a=0.1g，g为 重力加速度,不计摩擦,不计水浮力.
图(a)
（1）求开始提升时的瞬时，钢丝绳对弧形闸门的拉力 和质点对闸门钢架的支承力. （2）若以同样加速度提升同样重量的平板闸门[图(b)]
需拉力是多少？
FT
W
图(b)
[解]（1）以弧形闸门及钢架 为隔离体，受力如图(a)所示. 建立直角坐标系Oxy， 根据质心运动定理 FT FN W mac 向x及y轴投影得
考虑到
t
12v0 dr g 7lg v cos t cos( t) dt 2 24v0 7l
例：圆盘（R，M），人（m）开始静止，人
走一周，求盘相对地转动的角度.
1 I 2 MR 2 2
解： 系统对转轴 角动量守恒
M=0
I11 () I 22 0
I1 mR
2
人— ，盘— （对地的角位移） d d m 1 2 dt dt

I1d I 2 d
1 2 0
2
1 M 2
I d I d
0
2m 2 2m M
例：
圆盘质量M,半径R,J=MR2/2, 转轴光滑,人的质量m,开始时， 两者静止．求：人在盘上沿边 缘走过一周时，盘对地面转过 的角度．
in ex
角动量守恒定律是自然界的一个基本定律.

l l0
v0
v

20
解：由角动量守恒和机械能守恒可得
mv 0l0 mvl sin
1 mv 2 1 mv 2 1 k (l l ) 2 0 0 2 2 2
∴
l l0
v0
v

2 k ( l l ) 2 0 v v0 4 m s 1 m
v 0 l0 arcsin( ) 30 vl
4
22
已知
m 1.20 10 kg
4
h 100km
u 1.00 10 m s 2 g 1.62m s
4
1
R 1700km 求 所需消耗燃料的质量 m
vB
R
O B
. 解 设飞船在点 A 的 速度 v0 , 月球质量 mM , 由万有引力和牛顿定律
vA
M
m, v0
l
1 v f 4 v0
l f dt J f ldt
因,
ff
由两式得
3mv 0l 9mv 0 1 这里 J Ml 2 4J 4 Ml 3
例 质量很小长度为l 的均匀细杆,可绕过其中心 O 并与纸面垂直的轴在竖直平面内转动.当细杆静止于水平 位置时, 有一只小虫以速率v0 垂直落在距点O为 l/4 处, 并背离点O 向细杆的端点A 爬行.设小虫与细杆的质量均 为m.问:欲使细杆以恒定的角速度转动, 小虫应以多大速 率向细杆端点爬行? 解 小虫与细杆的碰撞视为完全非弹性碰撞，碰撞 前后系统角动量守恒
L Li mi ri 2 mi ri 2 J
i i i
式中
J mi ri
i
2

21
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
例：质量为Ｍ的圆锥摆摆球，以速率 v 运动时， 判断：1）对Ｏ参考点的角动量是否守恒？
2）对Ｃ参考点的角动量是否守恒？
2）以C为参考点。
重力矩：
r M
=
r l
×
mgr
M = lmg sin θ
张力矩：
r M
=
r l
×
r T
=
0
lθ c
16世纪末至17世纪初，开普勒仔细地分析整理了 前人记录下的大量精确的有关行星运动的资料，总 结出行星运动的规律、即开普勒三定律。
rrr
r M
=
rr ×
r F
=
i x
j y
k
r
r
r
z = Mxi + My j + Mzk
Fx Fy Fz
8
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
rrr
r M
=
rr
×
r F
=
i x
j y
k z
Fx Fy Fz
其中：
⎧ ⎪
M
x
=
yFz
−
zFy
⎨M y = zFx − xFz
r
注意：定理中的力矩和角动量都必须是相对于同 一参考点而言的。
说明: 1）冲量矩是质点角动量变化的原因。
2）质点角动量的变化是力矩对时间的积累结果。 17
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
四、质点的角动量守恒定律
当
v M
=
0
,
时，

内
外 外 外 质点系的
内
得
内 质点系所受的
内
外 外
冲量矩 质点系的角动量
矩的矢量和 的时间变化率 若各质点的速度或所受外力与参考点共面，则其角动量或力矩只含正 内力矩在求矢 反两种方向，可设顺时针为正向，用代数和代替矢量和。 量和时成对相消 微分形式 称为
外
角动量增量 质点受外力
刚体转动定律、质点系角动量守恒定律
即：
i j k Mo r F x y z Fx F y Fz i yFz zFy j zFx xFz k xFy yFx




M z xFy yFx
Mz为力对 o 点 的力矩在 z 轴方向的分量
注意. 力矩求和只能对同一参考点（或轴）进行。
另一类常见现象
刚体转动定律、质点系角动量守恒定律 ② J 可变，ω亦可变，但 Jω 乘积不变 茹可夫斯基櫈
张臂
大
用外力矩 启动转盘后 撤除外力矩
收臂 小 大
小
花样滑冰常见例
刚体转动定律、质点系角动量守恒定律 忽略脚底摩擦力矩的作用，角动量守恒 J1 J11 J 22 所以 2 1 J2
在冲击等问题中
M 内力 M外力 L 常量
角动量守恒定律是自然界的一个基本定律，有很多实例
刚体转动定律、质点系角动量守恒定律
角动量守恒现象举例 适用于一切转动问题，大至天体，小至粒子...
茹科夫斯基凳实验 为什么银河系呈旋臂盘形结构？ 为什么直升飞机的尾翼要安装螺旋桨？ 为什么猫从高处落下时总能四脚着地？
1 T1 r T2 r J mr 2 2
T1
r
(3)

称为质点系所受合外力矩 称为质点系所受合外力矩 对i , j 两个质点，内力矩之和为 两个质点，
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
(
)
(r
i
− rj
)
与 f ij 共线， 共线，
Mij + M ji = ri × f ij + r j × f ji = ri − r j × f ij = 0
角动量定理
Fdt = dP
t2 t2
dL M= dt M t = dL d
∫ Fdt =ΔP
t1
∫ Mdt =ΔL
t1
F = 0 P = 常矢量
F P
t2
M = 0 L = 常矢量
M L
t2
力 动量
力矩或角力 角动量 或动量矩
∫ Fdt 合力的冲量
t1
Mdt 合力矩的冲量 或冲量矩 ∫
t1
例
讨论行星运动
1 GMm 1 2 GMm 2 mv0 − = mv − 2 r0 2 R v0r0sinθ v= = 4v0sinθ mv0r0sinθ = mvR R
1 3GM sinθ = 1+ 2 4 2Rv0
1/ 2
3GM v = v01+ 2 2Rv 0
L
3、行星近地点速度大，在远地点速度小 、行星近地点速度大 地点速度小
在近日点与远日点
r ⊥v
v近
m r远
v远 =m r近 v近
v
v远 r远
r近
∴ v远 < v近
的光滑圆环置于竖直平面内.一质量为 例5-1 一半径为 R 的光滑圆环置于竖直平面内 一质量为 m 的小球穿在圆环上 并可在圆环上滑动 小球开始时静 的小球穿在圆环上, 并可在圆环上滑动. 止于圆环上的点 A (该点在通过环心 O 的水平面上 然后 该点在通过环心 的水平面上),然后 点开始下滑.设小球与圆环间的摩擦略去不计 设小球与圆环间的摩擦略去不计.求小球 从 A 点开始下滑 设小球与圆环间的摩擦略去不计 求小球 的角动量和角速度. 滑到点 B 时对环心 O 的角动量和角速度 解 小球受重力和支持力作 支持力的力矩为零,重力 用, 支持力的力矩为零 重力 矩垂直纸面向里

t=0
刚体定轴转动
ω ω
v
v
4. 线量与角量关系
dS = r ⋅ dθ
பைடு நூலகம்r a
切向分量 法向分量
dv dω at = = r = rα dt dt v2 an = = rω2 r
匀变速定轴转动
v v v v =ω×r
z
ω
v
20
r
O
dS
dθ P
匀变速直线运动
dS v= dt dv a= dt
v = v0 + at 1 2 S = v0t + at 2 2 v2 − v0 = 2aS
一对内力的力矩互相抵消 一对内力的力矩互相抵消 力矩
v v v v dL 量 M外 = 0时 = 0 L = ∑Li = 常 dt v M外 = 0 讨论; 不要求系统孤立, 讨论 1) 不要求系统孤立 只要求 v 2) 矢量式有 个分量式 即 M 的某个分量 矢量式有3个分量式 个分量式,即 的某个分量=0, 则相应角 外
v m ri i
∑
∑
角动量守恒说明天体系统的旋转盘状结构
12
猫尾巴的功能
已知：轻绳， 忽略滑轮的质量和轴的摩擦) 已知：轻绳，v10 = v20 =0，(忽略滑轮的质量和轴的摩擦) 问：m1= m2时，(A) m1先到；(B) m2先到；(C) 同时到 先到； 先到；
m1≠ m2时，(A) m1先到；(B) m2先到；(C) 同时到 若m1< m2 先到； 先到；
由角动量定理
r N
以向纸 内为正
O R
M外
dL r (爬) (不爬 mg 不爬) r 不爬 若 m1 > m2 : < 0, ∴ L < 0 m2g 爬 1 dt 轻的升得快； 有 m1v1 − m2 v2 < 0, ∴ v1 < v2 轻的升得快；

四 角动量定理、角动量守恒的应用
练习 电风扇开启电源时，经t1时间达到额定 转速 0 ，关闭电源时经t2时间停止。设电风扇的 转动惯量为 I ，且电机的电磁力矩与摩擦力矩为 恒量。求：电风扇电机的电磁力矩。 解. 风扇开启时，受电磁力矩 M与摩擦力矩 M f 的共同作用，经过时间t1，角速度0由增加 0 ， t 由角动量定理 t Mdt L L0 有
0
(M M f )t1 I0
即
I 0 (M M f ) t1
（ 1）
风扇关闭，受摩擦力矩 M f的共同作用，经过 时间t2，角速度由 0降低至零，由角动量定理有
M f t2 0 I0
即
I 0 Mf t2
（ 2）
由（1）式-(2)式 得
1 1 M I 0 ( ) t1 t 2
Nx
v0
m

例7 摩擦离合器 飞轮1：I1、 摩擦 轮2： I2 静止，两轮沿轴向结合，结合后两 轮达到的共同角速度。
解：两轮对共同转轴的角动量守恒
2 1
试与下例的齿轮啮合过程比较。
例8 两圆盘形齿轮半径r1 、 r2 ，对通过盘心 垂直于盘面转轴的转动惯量为I1 、 I2，开始 1 0 转动，然后两轮正交啮合，求啮合后 轮以 两轮的角速度。 解： 两轮绕不同轴转动，故对 两轴分别用角动量定理：
3-3 刚体定轴转动的角动量定理及其守恒
一、 刚体定轴转动的角动量定理 如前所述：刚体作为质点系的特例，显然应 当服从质点系角动量定理
dLZ 沿固定轴(z轴)的分量式为 M z dt
dL M dt
对于定轴转动的刚体，常常略去下标，即
dLபைடு நூலகம்M dt
称刚体定轴转动的角 动量定理的微分形式

定义：对O点力矩 大小
M r F
M Fr sin Fr 量纲： M ML2T 2 SI Nm

质点的角动量定理
dL M dt
< 180°
质点对某固定点所受的合外力矩等于它对该点角动量的时间变化率
动量定理
t2
Fd t Δ P
dt
?
Mz
Oi
vi
ri mi ri
Fi
Fiz
i
（垂直z轴） roi Fi ri Fi riz Fi
riz
Fi
Mz M iz ri Fi sin i
（垂直z轴） M iz | ri Fi | ri Fi sin i ri Fi
的方向, 这时质点系的角动量守恒
ex ri f i 0
M外 0
例 光滑水平桌面上放着一质量为
M的木块, 木块与一原长为L0, 劲度系数为k的轻弹簧相连, 弹 簧另一端固定于O点.当木块静 止于A处时, 弹簧保持原长, 设 一质量为m的子弹以初速 v0水 平射向M并嵌在木块中. 当木块 运动到 B (OBOA)时, 弹簧的 m 长度为L.
' (rc ri ) Fi i ' rc Fi (ri Fi )
i i
i
' dp dLc rc Fi (ri Fi ) rc dt dt i i
dp dp rc Fi rc F合外力 Fi 由质心运动定理 dt dt i i dLc dLc ' 质心参考系的 即 Mc (ri Fi ) 角动量定理 dt dt i （对质心的合外力矩等于对质心的角动量的时间变化率） 注意： 质心可以是动点，上式对非惯性系也成立！ 前面的角动量定理只对固定点和惯性系才成立 ex 讨论: 1) 若质点所受外力是 有心力, 即 f i 沿着或背着 ri

的质元受阻力矩大，
细杆的质量密度 m
l
质元质量 dm dx
o
xl dm m dx
x
质元受阻力矩：
dM 阻 dmgx
细杆受的阻力矩
m l
M阻
dM
阻
0l
gxdx
1 2
gl 2
1 2
mgl
24
转动中的功和能
一. 力矩的功
设刚体上P点受到外力 F 的作用， z
位移为 d
r,
dW F ds
功为 d
三. 匀变速转动公式
当刚体绕定轴转动的角加速度为恒量时，刚
体做匀变速转动 .
质点匀变速直线运动 刚体绕定轴作匀变速转动
v v0 at
x
x0
v0t
1 2
at 2
0 t
0
0t
1 2
t 2
v2 v02 2a(x x0 )
2 02 2 ( 0 )
5
定轴转动刚体的 转动定律 力矩 角动量 转动惯量
Li
质元mi对转轴Z的角动量为：
x
Liz
Li
cos( π 2
)
mi Riv i
sin
mi ri vi
对组成刚体的所有质元的角动量求和
z
vi
mi
ri Li
Ri
O
y
Lz Liz (rimivi) (miri2)ω
9
Lz Liz miri2 ( miri2 )
i
i
i
令 J miri2
刚体绕OZ轴转动的转动惯量
i
Lz Jω
刚体绕OZ轴转动的角动量
注意：
转动惯量、角动量都是相对量，都必须指明它们是

62钟摆绕o轴转动惯量jo等于杆绕o的转动惯量加上盘绕o的转动惯量63圆环转轴通过中心与盘面垂直常见刚体转动惯量64薄圆盘转轴通过中心与盘面垂直圆柱体转轴通过中心与几何轴垂直12mlmr细棒转轴通过中心与棒垂直12细棒转轴通过端点与棒垂直672r球体转轴沿直径2r球壳转轴沿直径68质点系的角动量定理
可能出现的情况是
（请点击你要选择的项目）
（4）以上结果都不对。
小议分析
质点系 若 T1 T2
系统的末 态角动量 忽略轮、绳质量及轴摩擦 系统受合外力矩为零，角动量守恒。 系统的初 态角动量 不论体力强弱，两人等速上升。
得
若 同高从静态开始 往上爬
系统受合外力矩不为零，角动量不守恒。 可应用质点系角动量定理进行具体分析讨论。
某过程角动量守恒要求整个过程的每个瞬间的系统角动量 保持不变。 角动量守恒条件是合外力矩始终为零，而非冲量矩为零
（只要初末状态角动量相等）
O

m
t2
b
O
t1
M dt L2 L1
以O’为参考点，球运动一周，始末状态角动量 相等，但是这个过程角动量不守恒。
L mvb
π （b与v夹角为 ） 2
( e)
( e)
外力矩：系统所受外力对质点i 的
力矩
量定理
对其中的一个质点i而言：
Li ri Fi ri (Fi (i ) Fi (e) ) Mi (i ) Mi (e)
对整个质点系而言：
(i ) (e) dLi dL (i ) (e) ri ( Fi Fi ) M i M i dt dt i i i i
质点所受合外力的冲量矩等于质点角动量的增量. 这是质点角动量定理的积分形式

本文首先回顾了功、势能、动能等基本概念，以及质点的动能定理，为后续引入角动量概念打下基础。接着，通过讨论绕固定轴转动的圆盘系统总动量为零的问题，指出不宜使用动量来量度转动物体的机械运动量，从而引入了与动量对应的角量——角动量。详阐述了角动量的定义、物理意义及计算方法，包括质点对点的角动量、质点对参考点的角动量等，并讨论了不同运动情况下角动量的变化特性。进一步，本文推导了角动量定理的微分形式和积分形式，揭示了力矩与角动量变化之间的关系。此外，还将角动量定理推广至质点系，得到了质点系角动量定理，并辨析了总外力矩与合外力力矩的区别。最后，本文探讨了刚体定轴转动的角动量，展示了角动量在刚体转动中的应用。通过本文的阐述，读者可以全面深入地理解含角动量的动能定理及其相关概念。

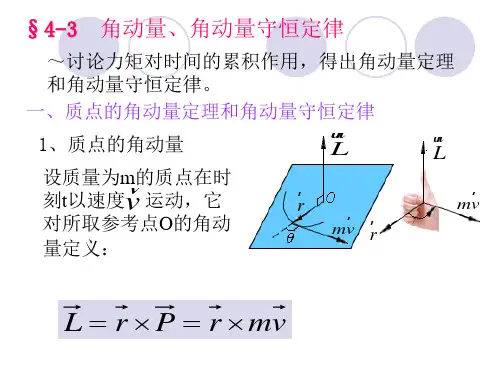
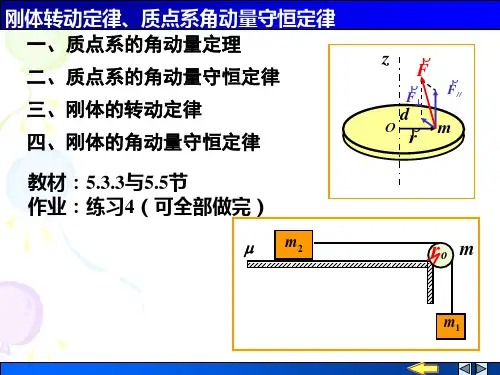
质心系角动量定理是经典力学中的一个重要定理，它表述了质点系在质心参考系中的角动量守恒定律。

这个定理在许多领域都有着广泛的应用，例如行星运动、陀螺仪、碰撞等问题。

首先，让我们了解一下质心系角动量定理的基本概念。

质心系角动量是描述质点系相对于质心转动的物理量，由质点的位置、速度和质心位置决定。

在质心参考系中，质点系的角动量是一个常数，这个常数不随时间变化。

接下来，我们探讨质心系角动量定理的证明过程。

首先，我们选取一个质点系和一个与质心固连的参考系，该参考系的原点即为质心的位置。

然后，我们计算质点系相对于质心参考系的角动量，得到每个质点的位置、速度和质心位置的函数。

由于质心参考系是惯性系，我们可以利用牛顿第二定律分析质点系的动力学行为。

通过对角动量表达式进行微分，我们发现角动量的时间导数为零，从而证明了质心系角动量定理。

最后，我们探讨质心系角动量定理的应用。

首先，在行星运动问题中，行星绕太阳的转动可以看作是一个质点系，太阳的位置即为质心。

应用质心系角动量定理，我们可以得到行星轨道的稳定性，进而研究行星运动的规律。

其次，在陀螺仪问题中，应用质心系角动量定理可以研究陀螺仪的进动和章动问题，进而设计高性能的陀螺仪。

此外，在碰撞问题中，应用质心系角动量定理可以研究碰撞后物体的运动状态，进而分析碰撞的力学性质。

综上所述，质心系角动量定理是经典力学中的一个重要定理，它表述了质点系在质心参考系中的角动量守恒定律。

这个定理在许多领域都有着广泛的应用，例如行星运动、陀螺仪、碰撞等问题。

通过深入理解质心系角动量定理，我们可以更好地掌握经典力学的原理和应用。

M
α
I
有何联系?
13
实验指出,定轴转动的刚体的角加速度 α与刚体所受的合外 力矩 M 成正比,与刚体的转动惯量 I 成反比.
v dω v M = Iα = I dt
v
定轴转动定理
v v F = ma
定轴转动定律在转动问题中的地 位相当于平动时的牛顿第二定律
应用转动定理解题步骤与牛顿第二定律时完全相同.
1 1 2 2 2 Eki = miυi = mi ri ω 2 2
质点质量 整个刚体的动能:
N
圆周运动的速率和半径
1 N 2 2 Ek = ∑Eki = (∑mi ri )ω 2 i=1 i=1
刚体对转轴的转动惯量:I
7
刚体定轴转动动能公式
物体的平动动能(质点动能)
1 2 Ek = Iω 2
角速度 ω 转动惯量 I 物体绕轴的转动惯性
λ :质量线密度 σ :质量面密度 ρ :质量体密度
10
I = ∫ r 2dm
单位: kg m2
转动惯量的大小取决于刚体的质量,质量分布及转轴的位置.
O
O l/2 O′
1 I= ml2 12
O
O O′
1 2 I = ml 3
r
O′
1 I = mr2 4
O′
1 I = mr2 2
11
平行轴
垂直轴
平行轴定理 质量为 m 的刚体,如果对其质心轴的转动惯量为 IC,则对任 一与该轴平行,相距为 d 的转轴的转动惯量:
2 θ 3Rω0 n= = 2π 16π g
26
讨论
用定轴转动的动能定理较之用转动定律求解, 省去了求角加速度,而直接求得,更为简捷.