5.3质点系对质心的角动量定理和守恒定理

椭圆轨道角动量守恒[4篇]以下是网友分享的关于椭圆轨道角动量守恒的资料4篇，希望对您有所帮助，就爱阅读感谢您的支持。

椭圆轨道角动量守恒（一）§5.3角动量守恒定律一、角动量守恒定律研究对象：研究对象：质点系由角动量定理：由角动量定理：当时，M x =0时L x =恒量分量式：分量式：M y =0时L y =恒量M z =0时L z =恒量对定轴转动刚体，对定轴转动刚体，当M=0时，L 轴=恒量角动量守恒定律：角动量守恒定律：当质点系所受外力对某参考点（当质点系所受外力对某参考点（或轴）或轴）的力矩的矢量和为零时，质点系对该参考点（质点系对该参考点（或轴）或轴）的角动量守恒。

的角动量守恒。

r守恒条件：：M 外=0注意1. 守恒条件能否为或rM d t =0外∫M 轴=0不能，不能，后者只能说明初、后者只能说明初、末态角动量相等，末态角动量相等，不能保证过程中每一时刻角动量相同。

不能保证过程中每一时刻角动量相同。

2. 与动量守恒定律对比：与动量守恒定律对比：r当M 外=0时，当F 外=0时，rp =恒矢量rL =恒矢量彼此独立例. 一半径为R 、质量为M 的转台，的转台，可绕通过其中心的竖直轴转动, 竖直轴转动, 质量为, 质量为m 的人站在转台边缘，的人站在转台边缘，最初人和台都静止。

台都静止。

若人沿转台边缘跑一周(不计阻力)不计阻力) ，相对于地面，于地面，人和台各转了多少角度？人和台各转了多少角度？思考：思考：1.台为什么转动1. 台为什么转动？向什么方向转动？台为什么转动？向什么方向转动？2.人相对转台跑一周 2. 人相对转台跑一周，人相对转台跑一周，相对于地面是否也跑了一周？否也跑了一周？3.人和台相对于地面转过的角度之间 3. 人和台相对于地面转过的角度之间有什么关系？有什么关系？解：选地面为参考系，选地面为参考系，设对转轴人：J , ω; 台：J ´, ω´J =mRJ ′=MR22系统对转轴合外力矩为零，系统对转轴合外力矩为零，角动量守恒。

质点动力学的三个基本定律
质点动力学的三个基本定律分别是：牛顿运动定律，动量定理和动量守恒定律，角动量定理和角动量守恒定律。

牛顿运动定律第一定律(惯性定律):任何质点如不受力的作用，则将保持原来静止或匀速直线运动状态。

第二定律:质点的质量与加速度的乘积等于作用于质点的力的大小，加速度的方向与力的方向相同。

第三定律:对应每个作用力必有一个与其大小相等、方向相反且在同一直线上的反作用力。

物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量(用字母I表示)，即力与力作用时间的乘积，数学表达式为：
I=FΔt=Δp=mΔv=mv2-mv1
式中F指物体所受的合外力，mv1与mv2为发生Δt的初末态动量。

该式为矢量式，列式前一定要规定正方向！
动量守恒定律是现代物理学中三大基本守恒定律之一，若一个系统不受外力或所受合外力为零时，该系统的总动量保持不变。

角动量守恒定律是物理学的普遍定律之一，反映质点和质点系围绕一点或一轴运动的普遍规律；反映不受外力作用或所受诸外力对某定点（或定轴）的合力矩始终等于零的质
点和质点系围绕该点（或轴）运动的普遍规律。

角动量守恒定律是对于质点，角动量定理可表述为质点对固定点的角动量对时间的微商，等于作用于该质点上的力对该点的力矩。

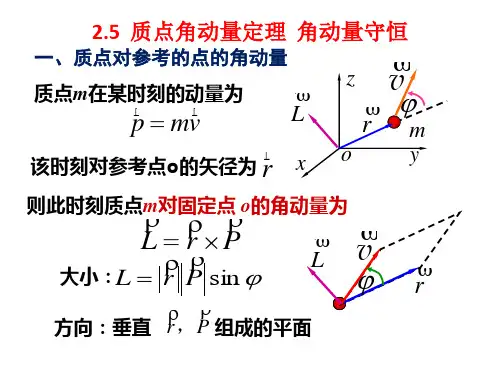
角动量定理1.质点的角动量开普勒描述行星运动时曾谈到行星沿平面轨道运行，若以太阳中心为参考点，其位置矢量在相等时间内扫过的面积相等。

这一描述是以日心恒星坐标系为参考系的。

将行星视为质点，分别用 r 和 v 表示行星的位置矢量和速度， vdt 表示质点在时间 dt 内的位移。

利用矢量矢积概念，dt 内位置矢量扫过面积的大小可用 \left| r×\frac{vdt}{2} \right| 表示，掠面速度大小为 \left| r×\frac{v}{2} \right| .r×\frac{v}{2} 的方向恰好与纸面垂直，它的方向不变可用来表示轨道在一平面内。

于是称矢量r×\frac{v}{2} 为掠面速度，即：r×\frac{v}{2} =常矢量.质点对于参考点的位置矢量与其动量的矢积：L=r×mv=r×p ；称质点对该参考点的角动量(或动量矩)。

受力质点相对于参考点的位置矢量与力的矢积：M=r×F；称力F对参考点的力矩。

2.质点的角动量定理和守恒定律①对参考点：由：\frac{d}{dt}(r×mv)=\frac{dr}{dt}×mv+r×\frac{d}{dt}(mv)=r×\fr ac{d}{dt}(mv)则， \Sigma F_i=\frac{d}{dt}(mv)\Rightarrow r×\SigmaF_i=r×\frac{d}{dt}(mv)\Rightarrow M=\frac{dL}{dt}即质点对参考点的角动量定理。

若M=0，则L=常矢量；即质点对参考点的角动量守恒定律。

②对轴线：在惯性系中取参考点O，过O点取z轴，质点对参考点O的角动量定理在z上的投影为：M_z=\frac{dL_z}{dt} ;质点对z轴的角动量对时间的变化率等于作用于质点的合力对同一轴线的力矩，称为质点对z轴的角动量定理。

质心参考系在力学教学中的重要性研究作者：霍海波范其丽来源：《经营管理者·上旬刊》2016年第04期摘要：在应用物理专业的教学过程中，有的知识点具有连续应用的特点，而这些知识点在定义时如果学生没能很好的掌握，结果就会导致在后续的学习过程中再遇到该类问题时，由于概念及定义掌握不牢固、印象不深，而出现理解上的问题。

久而久之，必定影响学生的学习积极性。

在力学的教学过程中，质心参考系就是这样一个连续应用的例子。

本文给出了质心参考系的定义，并总结了在力学及量子力学中质心参考系的连续应用，通过举例加深理解，以使学生能够很好的掌握关于质心参考系的定义，并能熟练应用。

关键词：质心参考系应用一、质心参考系的定义及相关定理力学是物理专业学生接触的第一门专业课，它有区别于中学物理中的力学，需要用矢量和微积分来处理问题，需要转变分析方法，同时也是后续课程学习的专业基础课，对物理专业的学生来说，地位十分重要。

在力学教学过程中，很多同学由于新接触一些物理概念，理解上会出现困难，结果此概念在后续章节的学习过程中持续出现，导致部分同学理解连续出现问题，影响学习积极性。

如质心参考系就是其中一个在力学教学中连续应用的概念。

由于质心参考系在力学学习中的重要性，在此首先给出质心和质心参考系的定义。

质心参考系示意图如图1所示图1 质心参考系示意图其中o～xyz为惯性参考系，o’～x'y'z’是以质心为坐标原点的质心参考系，设质点组中第i 个质点的质量为，相对于质心C的位矢为，质心坐标定义如下上式所确定的空间点和质点系密切相关，叫做质点系的质量中心，简称质心。

和XC，YC，ZC分别称为质心的位置矢量和质心坐标，它实际上是质点系质量分布的平均坐标。

如果为联系分布的刚体，则上式得求和符号变为积分。

在分析一些问题时，采用质心坐标系可以使问题简化，质心坐标系就是将坐标系变为o’～x'y'z’，一个显著特点是质心在质心坐标系中的位置矢量为零，根据这一特点，质心坐标系具有以下一些特性1.质点系质心运动定理即质点系总质量与质心加速度的乘积总是等于质点系所受外力的矢量和，这一点在我们分析力作用在物体不同位置时产生的复杂运动形式尤为重要，通过分析这些力的矢量和可以确定质心的运动状态，进而使问题简化。

质心系角动量定理是经典力学中的一个重要定理，它表述了质点系在质心参考系中的角动量守恒定律。

这个定理在许多领域都有着广泛的应用，例如行星运动、陀螺仪、碰撞等问题。

首先，让我们了解一下质心系角动量定理的基本概念。

质心系角动量是描述质点系相对于质心转动的物理量，由质点的位置、速度和质心位置决定。

在质心参考系中，质点系的角动量是一个常数，这个常数不随时间变化。

接下来，我们探讨质心系角动量定理的证明过程。

首先，我们选取一个质点系和一个与质心固连的参考系，该参考系的原点即为质心的位置。

然后，我们计算质点系相对于质心参考系的角动量，得到每个质点的位置、速度和质心位置的函数。

由于质心参考系是惯性系，我们可以利用牛顿第二定律分析质点系的动力学行为。

通过对角动量表达式进行微分，我们发现角动量的时间导数为零，从而证明了质心系角动量定理。

最后，我们探讨质心系角动量定理的应用。

首先，在行星运动问题中，行星绕太阳的转动可以看作是一个质点系，太阳的位置即为质心。

应用质心系角动量定理，我们可以得到行星轨道的稳定性，进而研究行星运动的规律。

其次，在陀螺仪问题中，应用质心系角动量定理可以研究陀螺仪的进动和章动问题，进而设计高性能的陀螺仪。

此外，在碰撞问题中，应用质心系角动量定理可以研究碰撞后物体的运动状态，进而分析碰撞的力学性质。

综上所述，质心系角动量定理是经典力学中的一个重要定理，它表述了质点系在质心参考系中的角动量守恒定律。

这个定理在许多领域都有着广泛的应用，例如行星运动、陀螺仪、碰撞等问题。

通过深入理解质心系角动量定理，我们可以更好地掌握经典力学的原理和应用。