当前位置：文档之家 › 第四章 方差分析

第四章 方差分析

  • 格式：ppt
  • 大小：533.00 KB
  • 文档页数：42

下载文档原格式

  / 42

合集下载

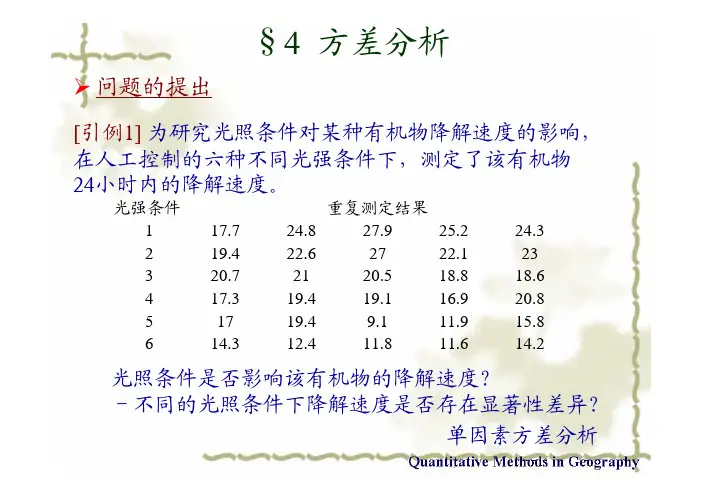
第四章+方差分析

第四章+方差分析

§4 方差分析¾问题的提出[引例1] 为研究光照条件对某种有机物降解速度的影响，在人工控制的六种不同光强条件下，测定了该有机物24小时内的降解速度。

光强条件重复测定结果117.724.827.925.224.3219.422.62722.123320.72120.518.818.6417.319.419.116.920.851719.49.111.915.8614.312.411.811.614.2光照条件是否影响该有机物的降解速度？－不同的光照条件下降解速度是否存在显著性差异？单因素方差分析¾问题的提出[引例2] 为比较3种松树在4个不同地区的生长情况有无差别，在每个地区对每种松树随机地选取5株，测量它们的胸径。

在不同地区松树的胸径是否存在显著性差异？双因素等重复方差分析¾问题的提出[引例3]为研究3种不同作物对污泥中镉吸收能力的差别，选择了4个地块进行栽培试验。

将每一个地块划分成三个小区，三种作物随机地分种在每个地块的三个小区上。

在所有地块上施用同等数量的污泥，作物收获后分别测定了其中镉的积累量（ug/kg)：不同作物对镉的吸收是否有显著性差异？不同地块下作物对镉的吸收是否有显著性差异？双因素无重复方差分析§4 方差分析¾研究论文¾利用t 检验进行2个以上总体均值比较的弊端¾检验过程烦琐¾无统一的试验误差，犯第I类错误的概率增大=2510C ααα−10.4’10＝0.05＝（1-）＝¾方法的提出英国统计学家R.A.Fisher于1923年提出方差分析方法(analysis of variance，ANOVA)。

方差分析的基本思想是：把全部数据关于总均值的离差平方和分解成几部分，每一部分表示某因素诸水平作用所产生的效应，将各部分均方与误差均方相比较，从而确认或否认某些因素或交互作用的重要性。

方差分析可用于多个样本均值的比较、分析多个因素的交互作用、方差的同质性检验、回归方程的显著性检验。

第4章 方差分析(anova)实验设计和分析

第4章 方差分析(anova)实验设计和分析

第4章方差分析（ANOV A）实验设计和分析Catherine Potvin4.1生态学问题弄懂生态学问题需要将各种环境因子的影响分开，生态工作者用实验来解决这个问题。

不论在野外还是在控制环境条件下，可控实验都可以让生态工作者们只变化一个因子来检验其影响。

例如，生长箱能使生物体生长在完全相同的温度而不同的光周期的条件下，或相同的光强而不同温度条件下的实验成为可能。

在控制实验中，通常最希望的情况是环境‘背景’，即所有的影响因子, 不是自由地变化，而是精确地得到控制，这样就能够保证在改变目标变量时，观测的反应不会受到其它因素的影响。

因而控制环境条件, 例如使用生长箱和温室，成为植物生态学的一个常用的方法，如同动物生态学中使用的生长柜和水族槽一样。

本章第一部分，我要讲一下作为实验生态学基本工具的方差分析（ANOV A）。

本章重点放在实验设计上。

虽然人们一般认为生长箱会提供同一环境条件，但不论在一个生长箱内还是生长箱间都存在环境异质性（Lee和Rawlings 1982；Potvin等1990a），因而能够充分处理环境异质性的实验设计将在本章中述及。

尽管我的论述主要是以生长箱实验为基础，其原理在其它类型的控制或野外环境的实验研究中同样适用（第5，15和16章）。

我还要讨论错误实验设计的代价。

本章应视为实验设计的起步点，这个起步点就是要考虑各种影响因素。

实验者通常进行的实验比这里展开的要复杂。

但是一旦懂得了基本原理，讨论各种实验设计就相对简单一些。

更详细的论述请见Cochran & Cox（1957）和Winter（1991）。

4.2 统计问题：环境变化与统计分析正如Underwood(1997)建议的一样，生态实验设计的第一步是建立一个线性模型使研究者能够将感兴趣的变量（因素）独立出来。

由于实验设计支配误差项，建立线性模型取决于所研究的因子以及具体的实验设计。

在任何一个实验开始时，最基本的是要检验空间与时间变化的格局。

第四章协方差分析

第四章协方差分析

MSe
1 n
xi• x•• E XX
2
(4 18)
即：各处理的方差应具备齐性，它们都是从具有 同一方差的正态总体中的来的；个处理的回归系
数i均等于以及反应变量与协变量之间的回归 系数≠0。因此，在对一组数据做协方差分析时，
首先要对以上各个条件做检验。只有以上条件得 到满足时，才能做协方差分析。
yij i (xij x•• ) ij
i 1,2,, a
j
1,2,, n
(4 1)
其中yij是第 i 次处理所得到的反应变量的第 j 次
观察值。cij是相当于yij的协变量值。c··是cij的 平均数，是总平均数，i是第i次处理效应， 是yij在cij上的线性回归系数，ij是随机误差成份。 做协方差分析，需要满足以下几个条件：ij是 服从正态分布的独立随机变量；≠0，即yij与cij
变差来源
平方 和
回归 处理
误差 总和
S2XY／SXX SS’e－SSe＝(SYY－S2XY／SXX)
－(EYY－E2XY／EXX) SSe＝EYY－E2XY／EXX
SYY
自由度 1
a－１
a(n－1)－1 an－1
均方 (SS’e－SSe)／(a－1)
F (SS’e－SSe)／ (a-1)／MSe
MSe＝SSe／[a(n－1)－1]
2
a i1
n j 1
yi2j
y•2• an
SXX
a i 1
n j 1
xij
x••
2
a i 1
n j 1
xi2j
x•2• an
a n
S XY
xij x••
i1 j1
yij y••

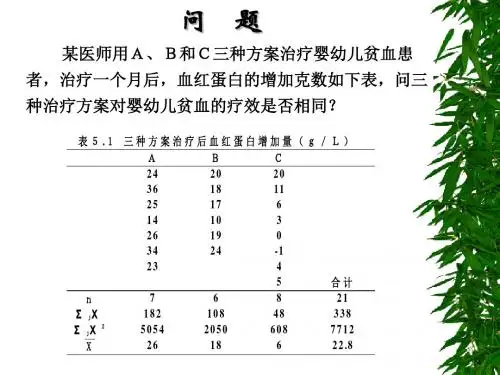
第四章 方差分析课件

第四章 方差分析课件

Ａ
Ｂ
Ｃ
24
20
20
36
18
11
25
17
6
14
10
3
26
19
0
34
24
-1
23
4
5
合计
n
7
6
8
21
Σ jΧ
182
108
48
338
Σ jΧ 2
5054
2050
608
7712
X
26
18
6
22.8
SS组内
(xij xi )2
ij
v组 内nk
组内均方 MS组内= SS组内/ 组内
三者关系：
1. SS总= SS组间＋ SS组内 2. 总 = 组间 ＋组内
4
5
合计
n
7
6
8
21
Σ jΧ
182
108
48
338
Σ jΧ 2
5054
2050
608
7712
X
26
18
6
22.8
表 ５ .１ 三 种 方 案 治 疗 后 血 红 蛋 白 增 加 量 （ ｇ ／ Ｌ ）
Ａ
Ｂ
Ｃ
24
20
20
36
18
11
25
17
6
14
10
3
26
19
0
34
24
-1
23
4
5
合计
n
7
6
8
21
Σ jΧ
6 108
8 48
21 338

第四章方差分析两向分组单因素区组二因素重复值拉丁方

第四章方差分析两向分组单因素区组二因素重复值拉丁方

变异 DF
来源
A因素 a-1
B因素 b-1
误 差
总变 异
(a1)(b-1)
ab-1
SS
MS
b ( yi. y.. )2 Ti.2 / b C
a ( y. j y.. )2
T.
2 j
/
a

C
MS A MS B
( y yi. y. j y.. )2 SST SSA SSB MSe
差异显著性
0.05
0.01
a
A
b
B
b
B
c
C
c
C
c
C
c
C
c
C
c
C
(2)各肥类平均数的比较
SE MSe bn 0.9283 3 0.32(g)
p
SSR 0.05 SSR 0.01 LSR 0.05 LSR 0.01
2
2.97
4.07
0.95
1.30 (dfe = 18)
3
3.12
4.27
F
混合模型EMS
(A固定，B随机)
MS A MS e

2

b
2 A
MS B

2

a
2 B
MS e
2
( yij y.. )2 y2 C
SSt = SSA + SSB DFt = DFA + DFB
注意：这种类型资料，其误差项是误差与 互作的混合项。因此只有AB不存在互作时， 才能正确估计误差。另外，为提高试验的 精确性。误差自由度不能小于12。
Tc
174 177 176 174 181 T=882

统计学第四章多个样本均数比较的方差分析

统计学第四章多个样本均数比较的方差分析
2
72.46
2.98
>0.05
区组间
2376.38
7
339.48
13.96
<0.01
误差
340.54
14
24.32总Βιβλιοθήκη 2861.8423
F0.01（7，14）=4.28， P<0.01。可认为8个区组的小白鼠体重增量有差别，即遗传因素对小白鼠体重增量有影响（但一般更关注处理组间差别的假设检验）。
02
单击此处添加正文，文字是您思想的提炼，请言简意赅地阐述您的观点。
第四章 多个样本均数比较的 方差分析
单击此处添加副标题
202X
方差分析
01.
方差分析的基本思想
单击此处添加正文
03.
随机区组设计的两因素方差分析
单击此处添加正文
05.
多个样本均数间的多重比较
单击此处添加正文
02.
完全随机设计的单因素
阶段
1
2
3
4
5
6
7
8
9
10
11
12
I
B
B
A
B
A
A
A
A
B
B
B
A
3.07
1.33
4.44
1.87
3.20
3.73
4.13
1.07
1.07
2.27
3.47
2.40
II
A
A
B
A
B
B
B
B
A
A
A
B
2.80
1.47
3.73
3.60
2.67
1.60

第四章 方差分析(二)

第四章 方差分析(二)

2.2 双因素方差分析
结果及解释 表4 显示，( 1）第一均衡子集（Subset = l 栏中）包含：
第二组（b = 2 ）、第三组（b = 3 ）和第四组（b = 4 ) ，它们的均数分别为47.67 、48.33 和53.00 。 三组均数比较的概率为0.070 。按0 . 05 检验水准， 接受无效假设，可认为工人2 、工人3 和工人4 日产量 的均数之间无明显差异。 ( 2 ）第二均衡子集（Subset = 2 栏中）包含：第四组 （b = 4 ）、和第一组（b = l ) ，它们的均数分别为 53 . 00 和55 . 00 。三组均数比较的概率为0.335 。 按0.05 检验水准，接受无效假设，可认为工人4 和工 人l 日产量的均数之间无明显差异。 ( 3 ）第一组（b =1）和第二、三、四（b = 2 、3 、 4 ）未列在均衡子集表的同一格子中，可以认为它们均 数并非均衡，而是存在显著差异。
2.2 双因素方差分析
结果及解释 表1显示( 1）分组变量a 有3个水平，即：机器A 、B、C ，每个水平有4例。( 2 ） 分组变量b 有四个水平，即：工人1 、2 、3 、4 ，每个水平有3 例。 表2 显示，( l ）因素a：F ＝均方a 因素／均方残差＝29.102 , P = 0.001 ，按住0.05 检验水准，拒绝无效假设，可认为机器之间差异显著，各机器间的日产量全 不等或不全等。 2 ）因素b：F ＝均方b 因素／均方残差＝6.985 , P = 0. 022 ， 按0.05 检验水准，拒绝无效假设，可认为工人之间差异显著，各工人间的日 产量全不等或不全等。
2.2 双因素方差分析
双因素方差分析的示例-双因素重复试验的方差分析
例4 设A , B , C共3 台机器生产同一产品，4 名工人机器A , B , C 都两天， 得日产量数据如表。

STATA第四章t检验和单因素方差分析命令输出结果说明

STATA第四章t检验和单因素方差分析命令输出结果说明

第四章 t检验和单因素方差分析命令与输出结果说明·单因素方差分析单因素方差分析又称为Oneway ANOVA,用于比较多组样本的均数是否相同，并假定：每组的数据服从正态分布,具有相同的方差，且相互独立，则无效假设。

原假设：H0:各组总体均数相同。

在STATA中可用命令：oneway 观察变量分组变量[, means bonferroni]其中子命令bonferroni是用于多组样本均数的两两比较检验。

例：测定健康男子各年龄组的淋巴细胞转化率(%)，结果见表，问:各组的淋巴细胞转化率的均数之间的差别有无显著性？健康男子各年龄组淋巴细胞转化率(%)的测定结果:11-20 岁组：58 61 61 62 63 68 70 70 74 7841-50 岁组：54 57 57 58 60 60 63 64 6661-75 岁组：43 52 55 56 60用变量x 表示这些淋巴细胞转化率以及用分组变量group=1，2，3分别表示11-20岁组，41-50岁组和61-75岁组,即：数据表示为：x 58 61 61 62 63 68 70 70 74 78 54 57 group 1 1 1 1 1 1 1 1 1 1 2 2x 57 58 60 60 63 64 66 43 52 55 56 60 group 2 2 2 2 2 2 2 3 3 3 3 3则用 STATA 命令：oneway x group, mean bonferroni| Summary of xgroup | Mean ①-------------+------------1 | 66.52 | 59.8888893 | 53.2------+------------Total | 61.25 ②Analysis of VarianceSource SS df MS F Prob > F-------------------------------------------------------------------------------Between groups 616.311111③ 2 ④ 308.155556⑤ 9.77⑥ 0.0010⑦Within groups 662.188889⑧ 21⑨ 31.5328042⑴-------------------------------------------------------------------------------Total 1278.50 23 55.586956（2）Bartlett's test for equal variances:chi2(2) = 2.1977 （3）Prob>chi2=0.333Comparison of x by group(Bonferroni)Row Mean- |Col Mean | 1 2-------------- --|--------------------------------------2 | -6.61111 （4）| 0.054 （5）|3 | -13.3 （6） -6.68889（8）| 0.001 （7） 0.134 （9）①对应三个年龄组的淋巴细胞转化率的均数；②三组合并在一起的总的样本均数；③组间离均差平方和；④组间离均差平方和的自由度；⑤组间均方和(即：⑤=③/④)；⑧组内离均差平方和；⑨组内离均差平方和的自由度；（1）组内均方和(即：（1）=⑧/⑨)；⑥为F 统计值(即为⑤/（1）)；⑦为相应的p值；（2）为方差齐性的Bartlett检验；（3）方差齐性检验相应的p值；（4）第二组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（5）第二和第一组均数差的显著性检验所对应p 值；（6）第三组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（7）第三和第一组均数差的显著性检验所对应的 p 值；（8）第三组的淋巴细胞转化率样本均数—第二组的淋巴细胞转化率的样本均数的差；（9）第三和第二组均数差的显著性检验所对应的p 值。

理学第四章方差分析

理学第四章方差分析

LSR0.01
q0.01
S x
表4 不同品种4个月增重量试验LSR值（q法）
M
2
3
4
q0.05
3.08
3.77
4.20
q0.01
4.32
5.04
5.50
LSR0.05 LSR0.01
4.65 6.52
5.69
6.34
7.61
8.30
3、三种方法的比较
表5 猪品种4个月增重量差异显著性比较表（Duncan法）
记字母法。这种方法首先将全部平均数以大到小依次排 列，然后在最大的平均数上标字母a，将该平均数与以下 各平均数相比，凡相差不显著的（〈 LSD）都标上字母a， 直至某个与之相差显著，则标以字母b。
在以该标有b的平均数为标准，与各个比它大的平均 数比较，凡差异不显著的在字母a的右边加标字母b。然 后再以标b的最大平均数为标准与以下未曾标有字母的平 均数比较，凡差异不显著的继续标以字母b，直至差异显 著的平均数标以字母c，在与上面的平均数比较，如此重 复，直至最小的平均数有了标记字母，并与上面的平均 数比较后为止。
b
A
表7 不同品种4个月增重量差异显著表(LSD检验)
平均数
差异显著性
xi
0.05
0.01
大白
30.9
a
A
沈花
27.9
ab
AB
沈白
25.8
b
AB
沈黑
24.1
b
B
根据上述检验计算，可以看到在跨距M=2时，LSD 法，SSR法和q检验的显著尺度是相同的。当 M 3时， 三种检验的显著尺度便不相同，LSD最低，SSR法次之， q检验法最高。因此，对于精度要求高的试验应用q检验， 一般试验可用SSR法。

第四章多个样本均数比较的方差分析

第四章多个样本均数比较的方差分析

第四章多个样本均数比较的方差分析方差分析的基本思想是通过比较各组或处理的均值差异与各组内的个体间差异来判断是否存在显著差异。

在进行方差分析之前，需要满足一些前提条件，如对总体的抽样是简单随机抽样、各样本之间是独立的等。

这些前提条件的满足保证了方差分析的可靠性。

多个样本的方差分析是通过计算组间离差平方和（SSTr）、组内离差平方和（SSE）和总离差平方和（SST）来比较各组或处理之间的差异。

计算公式为：SSTr = Σni(x̄i - x̄)²SSE = ΣΣ(xij - x̄i)²SST=SSTr+SSE其中，n是每组或处理的样本个数，ni是第i组或处理的样本个数，x̄i是第i组或处理的样本均值，x̄是全部样本的均值，xij是第i组或处理的第j个样本值。

通过计算SSTr和SSE，可以得到均方值（MS）：MStr = SSTr / (r - 1)MSE=SSE/(N-r)其中，r是组或处理的个数，N是总样本个数。

接下来，需要计算F值，用于判断各组或处理均值是否有显著差异：F = MStr / MSE根据F值和自由度，可以查找F表来确定是否存在显著差异。

如果F 计算值大于F临界值，则拒绝原假设，表示均值之间存在显著差异。

方差分析还可以进行多重比较，用于确定具体哪些组或处理之间存在显著差异。

常用的多重比较方法有Tukey的HSD（最大均值差异）和Bonferroni方法。

方差分析的优点是可以同时比较多个样本的均值差异，具有较好的统计效应。

然而，方差分析也存在一些限制，如对正态性和方差齐性的要求较高。

总之，多个样本均数比较的方差分析是一种常用的统计方法，在科学研究和实验设计中得到广泛应用。

它可以帮助研究人员确定不同处理或组之间的差异，为决策提供支持。

正交检验的极差分析和方差分析(教学课堂)

正交检验的极差分析和方差分析(教学课堂)

(Yij i )2
(Yij i )2
i1 j1
令下列各偏导数为零
S 0,
S 0
i
(i=1,2,…,k)
特选课堂
2
第四章 方差分析
4.1 方差分析的基本概念和原理
表 4－1 对6种型号生产线维修时数的调查结果
序号 型号
A型 B型 C型 D型 E型 F型
1
9.5 4.3 6.5 6.1 10.0 9.3
2
8.8 7.8 8.3 7.3 4.8 8.7
特选课堂
3
11.4 3.2 8.6 4.2 5.4 7.2
第四章 方差分析
4.2.1 数学模型和数据结构
其中：
i 纯属Ai作用的结果,称为在Ai条件下Yi的真值(也称为
在Ai条件下Yi的理论平均). i是实验误差(也称为随机误差)。
i ~ N (0, 2 ) （4-2）
Yi ~ N (i , 2 )
其中, 和 都是未知参数(i=1,2,…,k).
i 2
i 1
Mean),它是比
较作用大小的一个基点；
特选课堂
14
第四章 方差分析
4.2.1 数学模型和数据结构
并且称
i i
为第i个水平Ai的效应.它表示水平的真值比一般
水平差多少。满足约束条件
1 2 k 0
(4-6)
可得
Yij i ij ;
i 0
i=1,2,…,k ;j=1,2,…,m
…
Ykj
…
Ykm
特选课堂
合计
T1 T2
…
Ti
…
Tk
平均
Y1 Y2
…
Yi

第4章 方差分析

第4章 方差分析
4/46
浙江科技学院本科课程《化工数据处理》
方差分析基本思想：
方差分析，是按变异的不同来源，将全部观察值总的
离均差平方和和自由度分解为两个或多个部分，除随机误 差外，其余每个部分的变异可由某个因素的作用加以解释， 通过比较不同来源变异的均方（MS），借助F分布做出统 计推断，从而了解该因素对观察指标有无影响。
1 k i , i i k i 1
xij i ij
（4-1）
若令
则（4-1）式可以改写为
xij i ij
（4-2）
其中， 为全试验观测值总体平均数； 显然有
i 是第i个处理的效应，表示处理i对试验结果产生的影响。

i 1
k
1. 假定从第i个总体中抽取一个容量为ni的简单 2.
随机样本，第i个总体的样本均值为该样本的 全部观察值总和除以观察值的个数 计算公式为
xi
x
j 1
ni
ij
ni
(i 1,2,, k )
18/46
式中： ni为第 i 个总体的样本观察值个数 xij 为第 i 个总体的第 j 个观察值
浙江科技学院本科课程《化工数据处理》
12/46
浙江科技学院本科课程《化工数据处理》
三、问题的一般提法
1. 设因素有k个水平，每个水平的均值分别用 1 , 2, , k 表示 2. 要检验k个水平(总体)的均值是否相等，需要提 出如下假设： H0 ： 1 2 … k H1 ： 1 , 2 , ，k 不全相等
2. 3. 4.
差平方和 反映各总体的样本均值之间的差异程度，又称组 间平方和 该平方和既包括随机误差，也包括系统误差 计算公式为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

X 2.79 2.69 3.11 3.47 1.77 2.44 2.83 2.52
g 1 1 1 1 1 1 1 1
表 6.2 资料数据格式 X g X 3.83 2 5.41 3.15 2 3.47 4.70 2 4.92 3.97 2 4.07 2.03 2 2.18 2.87 2 3.13 3.65 2 3.77 5.09 2 4.26
• • • • • • • • • • • • • • • • • • • • • • • •
Data new; Do c=1 to 5; Input n; Do i=1 to n; Input x @@; Output; End; End; Cards; 6 21.5 19.5 20.0 22.0 18.0 20.0 6 16.0 18.5 17.0 15.5 20.0 16.0 5 19.0 17.5 20.0 18.0 17.0 4 21.0 18.5 19.0 20.0 4 15.5 18.0 17.0 16.0 ; Proc anova; Class c; Model x=c; Run;
过程步－－glm过程
proc glm; /*方差分析*/ class g; model x=g; means g/ hovtest snk ； run;
结果解释：
1、三组数据正态性检验作出判断
2、方差齐性检验：F=1.45，P=0.2567 >0.05，方差齐；
3、方差分析：F=4.28，P=0.0275，拒绝H0,差别有统计学 意义，三组小鼠FDP酶活力不全相等。
12.0 8.5 8.5 9.8 10.9 9.2 10.4 8.2 10.0
PROC ANOVA; CLASS a b; MODEL x=a b; RUN;
二.有重复的两因素方差分析
• 【例6.6】为了研究饲料中钙磷含量对幼猪生长发育的影 响，将钙(A)、磷(B)在饲料中的含量各分4个水平进行交 叉分组试验。先用品种、性别、日龄相同，初始体重基本 一致的幼猪48头，随机分成16组，每组3头，用能量、蛋 白质含量相同的饲料在不同钙磷用量搭配下各喂一组猪， 经两月试验，幼猪增重结果(kg)列于表6-29，试分析钙磷 对幼猪生长发育的影响。
棉布
府绸
的确凉
尼龙
2.33 2.00 2.93 2.73 2.33
2.48 2.34 2.68 2.34 2.22
3.06 3.06 3.00 2.66 3.06
4.00 5.13 4.61 2.80 3.60
程序如下：
DATA an; DO i=1 TO 4; DO a=1 TO 5; INPUT x @@; OUTPUT; END; END; CARDS; 2.33 2.00 2.93 2.73 2.33 2.48 2.34 2.68 2.34 2.22 3.06 3.06 3.00 2.66 3.06 4.00 5.13 4.61 2.80 3.60 ; PROC ANOVA; CLASS i; MODEL x=i; RUN;
一、方差分析的基本思想
根据资料的设计类型和研究目的，把全部观察值 的变异（总变异）分解为两个或多个部分，每 部分可以用某因素的作用来解释，将某因素解 释的变异和误差变异进行比较，作出某因素是 否有统计学意义的结论。
完全随机设计的方差分析表
变异来源
组间(处理组间) 组内(误差)
SS SS组间 SS组内
4 、两两比较：可以认为对照与水层RNA组间，对照组 与酚层RNA组间均有差别，而还不能认为水层RNA组与 酚层RNA组间有差别。
单因素方差分析 一.样本含量相等
某劳动卫生教研组研究棉布、府绸、的确凉、 尼龙四种衣料内棉花吸附十硼氢量。每种衣料各做 五次测量，所得数据如表。试检验各种衣料间棉花 吸附十硼氢量有没有显著差别?
Data new; Do c=1 to 5; Do i=1 to 6; Input x @@; Output; End; End; Cards; 21.5 19.5 20.0 16.0 18.5 17.0 19.0 17.5 20.0 21.0 18.5 19.0 15.5 18.0 17.0 ; Proc anova; Class c; Model x=c; Run;
过程步1---正态性检验
proc univariate normal; class g; var x;
run;
过程步2－－方差分析
proc anova; class g; model x=g;
run;
过程步3 －－方差分析同时输出统计表
proc anova;
class g;
model x=g;
DATA an; DO b=1 TO 8; DO a=1 TO 4; INPUT x @@; OUTPUT; END; END; CARDS;
8.4 12.8 9.6 9.4 15.2 9.1 9.8 12.9 11.2 12.2 14.4 9.8
9.8
8.8 8.4 8.6 8.9 7.9
9.9 8.2 9.9 9.0 8.1
受试者编 号 （区组） 1
2 3 4
处理组
1 2 3 4
8.4 12.8 9.6 9.8
9.4 15.2 9.1 8.8
9.8 12.9 11.2 9.9
12.2 14.4 9.8 12.0
5
6
8.4
8.6
8.2
9.9
8.5
9.8
8.5
10.9
7
8
8.9
8.4
9.0
9.4
9.2
9.8
10.4
10.0
二.样本含量不相等
• 5个不同品种猪的育肥试验，后期30天增重(kg)如表 6-16所示。试比较品种间增重有无差异。 • 表6-16 5个品种猪30天增重 • 品种 增 重 • B1 21.5 19.5 20.0 22.0 18.0 20.0 • B2 16.0 18.5 17.0 15.5 20.0 16.0 • B3 19.0 17.5 20.0 18.0 17.0 • B4 21.0 18.5 19.0 20.0 • B5 15.5 18.0 17.0 16.0
常用MODEL语句效应模型如下：
1）主效应模型
MODEL y=a ；（单因素方差分析模型） MODEL y=a b；（二因素方差分析模型） MODEL y=a b c；（三因素方差分析模型） 模型中，a ，b ，c 是主效应，y 是因变量 。
2）交互效应模型
MDOEL y=a b a*b MDOEL y=a b c a*b a*c b*c a*b*c； 模型中， a ，b ，c 是主效应， a*b，a*c ，b*c，a*b*c 是交互效应，y 是因变量。
MS区组/ MS误
差
总
二、 应用条件
独立性: 各样本是相互独立的随机样本 ; 正态性: 各样本来自正态总体; 方差齐性: 各总体方差相等。
不满足条件的处理
（1）轻微
– 允许应用t检验、方差分析来作分析。
（2）严重
– 数据转换
– 非参数统计
五、方差分析所用的过程
ANOVA过程(Analysis Of Variance)
means g；/*关于均数和标准差的统计表
*/
run;
过程步4－－方差分析同时进行方差齐性检验和两两比较
proc anova; class g; model x=g; means g/ snk; run; /*homogeneity of variance*/
过程步（完整）
proc univariate normal; /*正态性检验*/ class g; var x; run; proc anova; /*方差分析*/ class g; model x=g; means g/ hovtest snk ；(HOVTEST选项实现方差齐性检验) run;
表 6.1 对照组 2.79 2.69 3.11 3.47 1.77 2.44 2.83 2.52
三组小鼠的 FDP 酶活力 水层 RNA 组 酚层 RNA 组 3.83 5.41 3.15 3.47 4.70 4.92 3.97 4.07 2.03 2.18 2.87 3.13 3.65 3.77 5.09 4.26
高级生物统计
第四章 方差分析
目的与要求： （一）掌握内容 1. anova和glm过程的格式 2．能对SAS程序的输出结果作出合理解释 （二）熟悉内容 snk、Dunnett、Bonfferoni等多重比较方法 在SAS中的实现
过程简介
方差分析在SAS系统中由SAS/STAT模 块来完成，其中我们常用的有ANOVA过程 和GLM过程。前者运算速度较快，但功能较 为有限；后者运算速度较慢，但功能强大。 本章将首先介绍方差分析所用数据集的建立 技巧，然后重点介绍这两个程序步。
（3） MEANS语句是选择语句，计算并输 出所列的效应对应的因变量均数，若指明了 选择项，则将进行主效应均数间的检验。常 用的选择项如下：
• DUNCAN： 对MEANS语句列出的所有主效应均值进行DUNCAN检验。 • SNK： 对MEANS语句列出的所有主效应均值进行Student-Newman-Keuls检验。 • T | LSD： 对MEANS语句列出的所有主效应均值进行两两t检验，它相当于在样本含 量相同时的LSD检验。 • ALPHA＝ 均值间对比检验的显著水平，缺省值是0.05。当用DUNCAN选项时只能 取0.01、0.05和0.10，对于其它选项，α可取0.0001到0.9999之间的任何值。 • CLDIFF： 在选项T和LSD时，过程将两个均值之差以置信区间的形式输出。 • CLM： 在选项T和LSD时，过程把变量的每一水平均值以置信区间的形式输出。
22.0 15.5 18.0 20.0 .