第四章方差分析
- 格式:ppt
- 大小:6.55 MB
- 文档页数:7
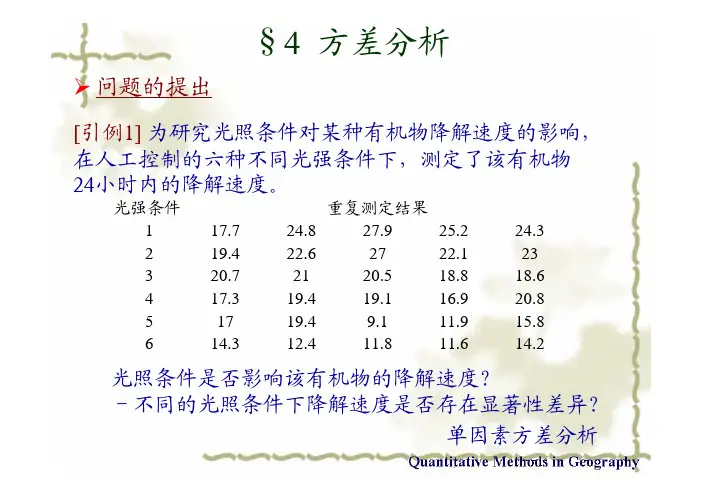
§4 方差分析¾问题的提出[引例1] 为研究光照条件对某种有机物降解速度的影响,在人工控制的六种不同光强条件下,测定了该有机物24小时内的降解速度。
光强条件重复测定结果117.724.827.925.224.3219.422.62722.123320.72120.518.818.6417.319.419.116.920.851719.49.111.915.8614.312.411.811.614.2光照条件是否影响该有机物的降解速度?-不同的光照条件下降解速度是否存在显著性差异?单因素方差分析¾问题的提出[引例2] 为比较3种松树在4个不同地区的生长情况有无差别,在每个地区对每种松树随机地选取5株,测量它们的胸径。
在不同地区松树的胸径是否存在显著性差异?双因素等重复方差分析¾问题的提出[引例3]为研究3种不同作物对污泥中镉吸收能力的差别,选择了4个地块进行栽培试验。
将每一个地块划分成三个小区,三种作物随机地分种在每个地块的三个小区上。
在所有地块上施用同等数量的污泥,作物收获后分别测定了其中镉的积累量(ug/kg):不同作物对镉的吸收是否有显著性差异?不同地块下作物对镉的吸收是否有显著性差异?双因素无重复方差分析§4 方差分析¾研究论文¾利用t 检验进行2个以上总体均值比较的弊端¾检验过程烦琐¾无统一的试验误差,犯第I类错误的概率增大=2510C ααα−10.4’10=0.05=(1-)=¾方法的提出英国统计学家R.A.Fisher于1923年提出方差分析方法(analysis of variance,ANOVA)。
方差分析的基本思想是:把全部数据关于总均值的离差平方和分解成几部分,每一部分表示某因素诸水平作用所产生的效应,将各部分均方与误差均方相比较,从而确认或否认某些因素或交互作用的重要性。
方差分析可用于多个样本均值的比较、分析多个因素的交互作用、方差的同质性检验、回归方程的显著性检验。


第四章⽅差分析第四章⽅差分析⼀、填空题1、⽅差分析就是通过对实验数据进⾏分析,检验⽅差时,各正态总体的是否相等,以判断各因素对试验指标的影响是否相等。
2、单因素⽅差分析的数学模型为。
3、在单因素⽅差分析中,总偏差平⽅和分解公式为。
4、对于具有s 个⽔平的单因素A 实验⽅差分析(⽔平i A 对应的总体为),(2σµi N (i =1,2,…,s ),现取样,设各⽔平下的样本容量之和为n ,以T e A S S S ,,分别表⽰因素A 的效应平⽅和、误差平⽅和、总偏差平⽅和,则(1)T e A S S S ,,之间的关系是___________;(2)在s µµ==...1成⽴的条下,~)/()1/(s n S s S E A --___________;(3)在显著性⽔平α下,假设“s H µµ==...:10,s H µµ,...,:11不全相等”的拒绝域形式是_________4、⽅差分析的⽬的是_______ .解:推断各因素对试验结果影响是否显著.5、在⼀个单因⼦试验中,因⼦A 有4个⽔平,每个⽔平下重复次数分别为:5,7,6,8 那么误差平⽅和的⾃由度,因⼦A 的平⽅和的⾃由度为。
6、单因素试验⽅差分析的数学模型含有的三个基本假定是_______ . 解:正态性、⽅差齐性、独⽴性.⼆、简述题1、简述⽅差分析解决什么问题。
2、单因素⽅差分析的数学模型是什么?3、单因素⽅差分析中的总偏差平⽅和分解公式是什么?4、单因素⽅差分析中,总偏差平⽅和、组间偏差平⽅和(因⼦平⽅和)、组内偏差平⽅和(误差平⽅和)分别是由什么引起的?5、⽅差分析的检验⼀般⽤什么检验法?6、⽅差分析的⽬的及思想(结合单因素)。
三、单选题1、⽅差分析是⼀个()问题。
A 、假设检验B 、参数估计C 、随机试验D 、参数检验2、在⽅差分析中,()反映的是样本数据与其组平均值的差异 A 总离差 B 组间误差 C 组内误差 D A,B,C 全错3、∑∑==-si n j i ij iX X 112)(是()B 组间平⽅和C 总离差平⽅和 D4、单因素⽅差分析中,数据i ij n j r i X ,,2,1;,,2,1, ==可以看作是取⾃()。

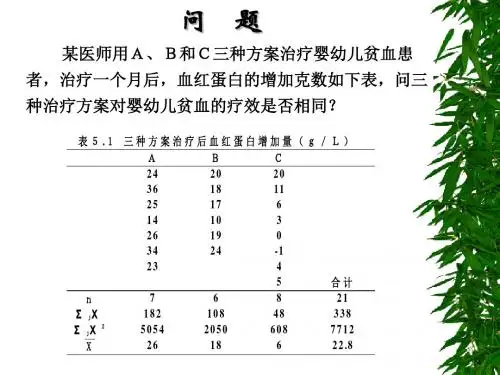




第四章多个样本均数比较的方差分析方差分析的基本思想是通过比较各组或处理的均值差异与各组内的个体间差异来判断是否存在显著差异。
在进行方差分析之前,需要满足一些前提条件,如对总体的抽样是简单随机抽样、各样本之间是独立的等。
这些前提条件的满足保证了方差分析的可靠性。
多个样本的方差分析是通过计算组间离差平方和(SSTr)、组内离差平方和(SSE)和总离差平方和(SST)来比较各组或处理之间的差异。
计算公式为:SSTr = Σni(x̄i - x̄)²SSE = ΣΣ(xij - x̄i)²SST=SSTr+SSE其中,n是每组或处理的样本个数,ni是第i组或处理的样本个数,x̄i是第i组或处理的样本均值,x̄是全部样本的均值,xij是第i组或处理的第j个样本值。
通过计算SSTr和SSE,可以得到均方值(MS):MStr = SSTr / (r - 1)MSE=SSE/(N-r)其中,r是组或处理的个数,N是总样本个数。
接下来,需要计算F值,用于判断各组或处理均值是否有显著差异:F = MStr / MSE根据F值和自由度,可以查找F表来确定是否存在显著差异。
如果F 计算值大于F临界值,则拒绝原假设,表示均值之间存在显著差异。
方差分析还可以进行多重比较,用于确定具体哪些组或处理之间存在显著差异。
常用的多重比较方法有Tukey的HSD(最大均值差异)和Bonferroni方法。
方差分析的优点是可以同时比较多个样本的均值差异,具有较好的统计效应。
然而,方差分析也存在一些限制,如对正态性和方差齐性的要求较高。
总之,多个样本均数比较的方差分析是一种常用的统计方法,在科学研究和实验设计中得到广泛应用。
它可以帮助研究人员确定不同处理或组之间的差异,为决策提供支持。
