湖北省安陆一中2012届高三数学 培优补差(二)

安陆一中2012届高三数学选填题专项训练(四)命题人：张秀平 审题人：董雄伟 2011.10 。

16班级 姓名一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知()1a i i a R i+=∈-，其中i 为虚数单位,则a 等于（ A ）A ．1B ．-1C ．2D ．02．已知角α的终边上一点的坐标为55(sin ,cos )66ππ，则角α的最小正角是（ C ）A ．56πB ．23πC ．53πD ．116π3．函数1()lg 3f x x x=--的零点所在区间为 ( C )A ．(0,1）B ．（1，2）C ．(2,3）D ．（3，+∞） 4．已知{}1||,1|||),(≤≤=Ωy x y x , A 是曲线122y x y x ==与围成的区域，若向区域Ω上随机投一点P ，则点P 落入区域A 的概率为 ( D ）A ．13B ．14C ．18D ．1125．设抛物线212y x =的焦点为F,经过点P （1，0）的直线l 与抛物线交于A ，B 两点,且2BP PA =，则||||AF BF +=（ D )A ．52B ．92C ．8D ．1726. 四棱锥S —ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是（ D )(A) AC ⊥SB （B ） AB ∥平面SCD(C ） SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 （D ）AB 与SC 所成的角等于DC 与SA 所成的角7. 某产品的广告费用x 与销售额y 的统计数据如下表 ( B )根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4，据此模型预报广告费用为6万元时销售额为［来源:Z§xx§k B(9（A ）63。

6万元 (B)65。

5万元 (C ）67。

7万元 (D ）72.0万元 8．已知向量OA ,OB 的夹角为60°，｜OA ｜=|OB ｜=2，若OC =2OA +OB ,则△ABC 为（ C ）A 。

2012届高三培优补差文科数学（七）一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只一项是符合题目要求的。

） 1．设集合{1,2}M =，则满足条件{1,2,3,4}MN =的集合N 的个数是（ ）A ．1B ．3C ．4D ．82．函数3()sin 1(),()2,()f x x x x R f a f a =++∈=-若则=（ ） A ．3B ．0C ．-1D ．-23．“a=1”是“直线(2)01ax a y x ay +-=-=和互相垂直”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4．若复数312a ii++（,a R i ∈为虚数单位）是纯虚数，则实数a = （ ） A ．-2 B ．4 C ．-6 D ．6 5．如图，底面为正方形，侧棱垂直于底面的四棱柱ABCD —A 1B 1C 1D 1中， AA 1=2AB ，则异面直线A 1B 与AD 1所成角的余弦值为 （ ） A ．15 B ．25C ．35D ．456．已知函数s i n ()(0)2y x πϕϕ=+<<的一条对称轴为43x π=，则ϕ值为 （ ）A ．56π-B ．3π C ．23π D ．6π 7．已知向量(1,2),(2,)a bλ=-=，且a b 与的夹角为锐角，则实数λ的取值范围是（ ）A ．(,1)-∞B ．（0，1） C．(1,)+∞D ．(,4)(4,1)-∞--8．若实数x ，y 满足2220350,(1)0,0x y x y x y x y -≤⎧⎪-+≥++⎨⎪>>⎩则的最大值是（ ）A ．B ．8C D 9．若圆C 与y 轴和直线3420x y +-=都相切，且圆心在第二象限，圆半径为2，则圆C 的标准方程为（ ）A ．2216()(2)43x y ++-= B ．229(2)()22x y ++-= C ．223(2)()42x y ++-= D ．229(2)()42x y ++-=10．某几何体的三视图如图所示，根据图中数据，可得该几何体的体积是 （ ）A ． BC ．D ．11．国家规定某行业征税如下：年收入在280万元及以下的税率为p%，超过280万元的部分按（p+2）%征税，有一公司的实际缴税比例为(0.25%)p +，则该公司的年收入是 （ ）A ．560万元B ．420万元C ．350万元D ．320万元12．数列{}n a 是各项均为正数的等比数列，且491,44a a ==，设II n 是数列{}n a 的前n 项积，即*12()n n II a a a n N =⋅∈，则（ ）A ．56II II <B ．56II II =C ．57II II =D ．67II II =二、填空题：（本大题共4小题，每小题4分，共16分，把答案填在相应横线上） 13．已知数列{}n a 是公差为2的等差数列，且125,,a a a 成等比数列，则2a = 。

安陆一中2012届高三数学选填题专项训练(五）命题人：李治国 审题人：徐友成班级 姓名 分数 一、选择题:本大题共10小题,每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 复数212m z -=+i i（m R ∈，i 是虚数单位）在复平面上对应的点不可能位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2。

下列说法错误的是（ )A ．自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系;B ．线性回归方程对应的直线错误!＝错误!x ＋错误!至少经过其样本数据点(x 1，y 1),（x 2,y 2）,…，（x n ，y n )中的一个点;C ．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高;D ．在回归分析中,2R 为0。

98的模型比2R 为0.80的模型拟合的效果好3. 若1sin()34πα-=，则cos(2)3πα+=( ）A ．78B ．14- C ．14D ．78-4。

已知函数()f x 对应关系如表所示，数列{}na 满足：113,(),n na a f a +==则2011a =（ ）A ．3B ．2C ．1D ．不确定5。

一个空间几何体的三视图如图所示,则该几何x 12 3 f （x ） 32 1第6题图第10题图体的表面积为（ )A.48B.32817+ C 。

48817+ D 。

806. 函数()y f x =在定义域3(,3)2-内可导,其图象如图所示，记()y f x =的导函数为'()y f x =，则不等式'()0f x ≤的解集为（ ）A ．31[,][1,2)22- B ．148[1,][,]233-C ．1[,1][2,3)3-D ．3148(,1][,][,3)2233-- 7。

某校在模块考试中约有1000人参加考试，其数学考试成绩2~(90,),N a ξ（0,a >试卷满分150分），统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的35，则此次数学考试成绩不低于110分的学生人数约为（ ）A ．200B ．300C ．400D ．6008. 把座位编号为1、2、3、4、5、6的六张观看《孔子》的电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的票必须是连号，那么不同的分法种数是（ )A ．96B ．144C ．156D ．196 9。

2012届高三培优补差文科数学（九）一． 选择题: (本大题共10小题, 每小题5分, 共50分． 在每小题给出的四个选项中, 只有一项是符合题目要求的)1．集合12{0,log 3,3,1,2}A =-，集合{|2,}xB y R y x A =∈=∈，则AB =A. {1}B.{1，2}C.{-3，1，2}D.{-3，0，1}2. 设集合A ={(,)|46}x y x y +=，{(,)|327},B x y x y =+=则=⋂B A ( ) (A){12}x y ==或 (B) {1,2} (C){(1,2)} (D) (1,2)3．已知向量a 、b 的夹角为60，且2=a ，1=b ，则向量a 与向量a ＋2b 的夹角等于（ ） (A) 150° (B) 90° (C) 60° (D) 30°7.．设集合A=⎪⎭⎫⎢⎣⎡21,0, B=⎥⎦⎤⎢⎣⎡1,21, 函数()1,2()21,,x x A f x x x B ⎧+∈⎪=⎨⎪-∈⎩若0x A ∈, 且0[()]f f x A ∈,则0x 的取值范围是 （ ） A ．⎥⎦⎤ ⎝⎛41,0 B ．⎥⎦⎤⎢⎣⎡83,0 C ．⎪⎭⎫⎝⎛21,41 D ．⎥⎦⎤⎝⎛21,418．在面积为S 的△ABC 内任投一点P ，则△PBC 的面积大于2S的概率是( ) （A ）31 （B ）21 （C ）43 （D ）41 9．方程22||1x x y +=满足的性质为 A ．对应的曲线关于y 轴对称 B ． 对应的曲线关于原点成中心对称 C ． x 可以取任何实数D ．y 可以取任何实数10．设函数252 , -2x 0()()log (5) , 0<x 2x f x g x x x ⎧≤<=⎨-++≤⎩，若()f x 是奇函数，则当x (0,2]∈时， ()g x 的最大值是（ ）A ．14B ．34-C ．34D ．14-二．填空题: （本大题有7小题, 每小题5分, 共35分）11．292925sin cos()tan()634πππ+-+-= 12．当太阳光线与地面成θ（)900︒<<︒θ角时，长为l 的木棍在地面上的影子最长为_____________ 13．已知tan()34πθ+=，则2sin 22cos θθ-＝ .14．已知函数()f x 满足()(4)f x f x =-，且当2x >时，()f x 是增函数，若0.9(1.2)a f =，1.2(0.9)b f =，13(log 9)c f =，则,,a b c 大小关系为 .15．已知向量11(,)a x y =，22(,)b x y =，33(,)c x y =，定义运算“*”的意义为1221(,)a b x y x y *=．则下列命题○1若(1,2),(3,4)a b ==，则(6,4)a b *=○2a b b a *=*○3()()a b c a b c **=**○4()()()a b c a c b c +*=*+*中，正确的是 ．16．如图，测量河对岸A 、B 两点间的距离，沿河岸选取相距40米的C 、D 两点，测得： ∠ACB=60°，∠BCD=45°，∠ADB=60°，∠三. 解答题: （本大题有5小题, 共65分）18. （本题12分）19．（本题13分）20．（本题13分）解关于x的不等式ax2+2x+2 a>021．（本题13分）已知23,03()1(3),3xx f x x f x +⎧≤≤⎪=+⎨⎪>⎩，（1）求函数()f x 的单调区间；（2）若关于x 的方程()0f x a -=恰有一个实数解，求实数a 的取值范围；22．（本题14分）已知函数21()ln 2(0).2f x x ax x a =--<（Ⅰ）若函数()f x 存在单调递减区间，求a 的取值范围；（Ⅱ）若12a =-且关于x 的方程1()2f x x b =-+在[]1,4上恰有两个不相等的实数根，求实数b 的取值范围；2012届高三培优补差文科数学（九）答案1．【答案】B 【解析】解：11{|2,}={1,2,4,,}A B={1,2}83x B y R y x A =∈=∈∴⋂2.【答案】C 【解析】解：解方程组可知4613272解得x y x x y y +==⎧⎧⎨⎨+==⎩⎩故得到一个公共点，则交集为单元素点集，故选C 3．【答案】D4πππ()3sin 22=k ,332k 5π,212k ππππ,0),2[2-,[2+],26322π5π[,],,1212ππ()3sin 2()3sin 2-33的对称轴方程为令对称中心为(递增区间为当k=0时，选项C 满足题意。

2012届高三数学第二次综合试题（文科） 一、选择题(10小题，每小题5分，满分50分) 1. 化简复数得 A. B. C. D. 2. 已知集合，，若，则 A. B. C. 或 D. 或 3. 若曲线在点处的切线方程是，则 A. B. C. D. 4. 已知为不重合的两个平面，直线，那么“”是“”的A. 充要条件B. 必要而不充分条件C. 充分而不必要条件D. 既不充分也不必要条件 5. 将函数的图像向左平移个单位，再向下平移个单位，得到函数的图像，则的解析式为 A. B. C. D. 6. 设是定义在上的周期为的周期函数，如下图表示该函数在区间上的图像，则 A. B. C. D. 7. 某校对高三年级的学生进行体检，现将高三男生的体重（单位：）数据进行整理后分成五组，并绘制频率分布直方图（如上图所示）.根据一般标准，高三男生的体重超过属于偏胖，低于属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为，，，，第二小组的频数为，则该校高三年级的男生总数和体重正常的频率分别为 A. B. C. D. 8. 已知流程图如下图所示，该程序运行后，为使输出的值为，则循环体的判断框内① 处应填的是 A. B. C. D. 9. 已知等差数列前项和，则 A. B. C. D. 10. 定义在区间上的函数的图像如下图所示，记以，， 为顶点的三角形的面积为，则函数的导函数的图像大致是 题号12345678910答案 二、填空题(5小题，每小题5分，满分25分) 11. 已知，，则 . 12. 已知均为正数，且，则的最小值为 . 13. 设数列的前项和为，且，则数列的通项公式是 . 14. 设函数的定义在上的偶函数，且是以为周期的周期函数，当时，，则与的大小关系为 . 15. 一个三角形数阵如下： …… 按照以上排列的规律，第行从左向右的第个数为 . 三、解答题（本大题6小题，满分75分） ，，，向量.（1）若向量与共线，求实数的值；（2）若向量，求实数的取值范围. 17.（12分）某学校共有教职工900人,分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 . 第一批次第二批次第三批次女教职工196xy男教职工204156z （1）求的值；（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名？（3）已知，求第三批次中女教职工比男教职工多的概率.如图，在面体中，平面∥平面，平面，,,∥，且, ． （1）求证：平面平面； （2）求证：∥平面； （3）求三棱锥的体积．的各项均为正数，且前项之和满足，且，，成等比数列.（1）求数列的通项公式；（2）若数列的前项和为，求. 20.（13分）函数．（Ⅰ）若，在处的切线相互垂直，求这两个切线方程（Ⅱ）若单调递增，求的范围．等差数列中，首项，公差，前n项和为，已知数列成等比数列，其中，，．（Ⅰ）求数列，的通项公式；（Ⅱ）令，数列的前n项和为．若存在一个最小正整数M，使得当时，（）恒成立，试求出这个最小正整数M的值．2012届高三数学第二次综合试题（文科）参考答案 一、选择题1. D2. D3. A4. C5. B6. A7. D8. B9. A 10. D 二、填空题 11． 12. 13. 14. 15 . 三、解答题 16. （本小题满分12分） 解：（I） 又 （II） 17. （本小题满分12分） 解: (1)由,解得. (2)第三批次的人数为, 设应在第三批次中抽取名，则，解得. ∴应在第三批次中抽取12名. （3）设第三批次中女教职工比男教职工多的事件为，第三批次女教职工和男教职工数记为数对，由（2）知，则基本事件总数有： ，共9个， 而事件包含的基本事件有：共4个， ∴. 解:（1）∵平面∥平面，平面平面, 平面平面 ., ∴为平行四边形，. 平面,平面， 平面, ∴平面平面. （2）取的中点为，连接、， 则由已知条件易证四边形是平行四边形， ∴，又∵， ∴ ∴四边形是平行四边形，即， 又平面 故 平面. （3）平面∥平面，则F到面ABC的距离为AD. ＝II），公比，所以前项和为 20. （本小题满分13分） 解：（I）, ∴ ∵两曲线在处的切线互相垂直 ∴ ∴ ∴ ∴在 处的切线方程为， 同理，在 处的切线方程为 (II) 由 得 ∵单调递增 ∴恒成立 即 令 令得，令得 ∴∴的范围为 解：（Ⅰ）由，得，解得，， ，又在等比数列中，公比，∴， ，． （Ⅱ）， 则， 两式相减得： ， ∴． ∵， ∴单调递增，∴．又在时单调递增． 且，；，；，；，；…． 故当时，恒成立，则所求最小正整数M的值为3． 第18题图 第10题图 第8题图 第6题图 第7题图。

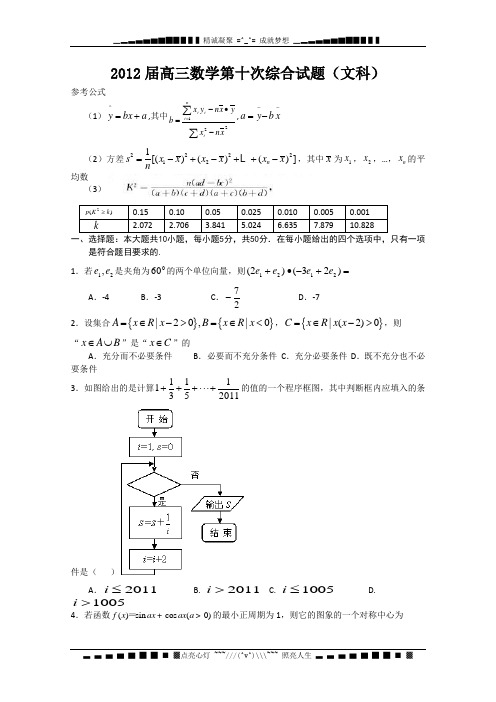
2012届高三数学第十次综合试题（文科）参考公式（1）^y bx a =+,其中∑∑-∙-==221xn xy x n yx b ini ii ,a y b x --=-（2）方差2222121[()()()]n s x x x x x x n=-+-++-，其中x 为1x ，2x ，…，n x 的平均数 （3）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的. 1．若21,e e 是夹角为060的两个单位向量，则=+-∙+)23()2(2121e e e eA ．-4B ．-3C ．27-D ．-72．设集合{}{}|20,|0A x R x B x R x =∈->=∈<，{}|(2)0C x R x x =∈->，则“x A B ∈⋃”是“x C ∈”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件3．如图给出的是计算2011151311+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是（ ）A ．2011≤i B. 2011>i C. 1005≤iD. 1005>i4．若函数()sin cos (0)f x ax ax a +>＝的最小正周期为1，则它的图象的一个对称中心为A ．)0,8(π-B ．（0，0）C ．1(,0)8-D ．1(,0)8 5．《莱茵德纸草书》是世界上最古老的数学著作之一。

书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的71是较小的两份之和，问最小的一份为A ．35B ．310C ．5D ．3206．定义在R 上的偶函数(f x ），当0()2xx f x ≥=时，，则满足()821<-x f 的x 取值范围是A ．(-1,2)B ．(-2,1)C ． [-1,2]D ．(-2,1].7．某四面体三视图为如图所示的三个直角三角形，则该四面体四个面的面积中最大的是A ．B ．C ．10D ．8．为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁~18岁的男生体重（kg ），得到频率分布直方图如下根据上图，可得这100名学生中体重在).,.[564556的学生人数是A ．20B ．40C ．60D ．809．若曲线1C ：0222=-+x y x 与曲线2C ：0)(=--m mx y y 有四个不同的交点，则实数m 的取值范围是A ．)33,33(-B ．)33,0()0,33(⋃-C ．]33,33[-D ．),33()33,(+∞⋃-∞ 10．某工厂产生的废气经过过滤后排放，在过滤过程中，污染物的数量p （单位：毫克/升）不断减少，已知p 与时间t （单位：小时）满足关系：3002)(t p t p -=，其中0p 为t=0时的污染物数量，又测得当t=30时，污染物数量的变化率是2ln 10-，则p(60)=A ．150毫克/升B ．300毫克/升C ．150ln2 毫克/升D ．300ln2毫克/升二、填空题：本大题共7小题，每小题5分，共35分．请将答案填在答题卡中相应的位置 11．复数=-+ii11--------12．已知线性回归方程ˆ129ybx x y b =+===，若，，则------- 13．某班数学兴趣小组有男生和女生各３名，现从中任选２名学生去参加校数学竞赛，则 至少有一名参赛学生是男生的概率为.------------14．已知⎪⎩⎪⎨⎧≤--≥+-≥-+033042022y x y x y x ，则22y x +的取值范围是-----------15．ABC ∆中a 、b 、c 分别为内角A 、B 、C 所对的边，,2,3==b a 且,0)cos(21=++C B 则BC 边上的高等于----------------16．已知曲线C 的方程为1122=-+ky k x ，则当C 为双曲线时，k 的取值范围是;------------- 当C 为焦点在y 轴上的椭圆时，k 的取值范围是.------------------17．已知0,0>>b a 且⎪⎩⎪⎨⎧+=22ba b ah )()(2222b a b a b a ba +>+≤则h 的最大值等于---------三、解答题：本大题共6个小题，共75分．解答应写出文字说明，证明过程或演算步骤 18．（本题满分12分）：设函数)(,sin 22cos sin 622)(2R x x x x x f ∈-+=（I ）对)(x f 的图像作如下变换：先将)(x f 的图像向右平移12π个单位，再将横坐标伸长到原来的2倍，纵坐标不变，得到函数)(x g 的图像，求)(x g 的解析式；（II ）已知ππ<<<<2120x x ，且2)(,526)(21==x g x g ，求)tan(21x x +的值。

2012届高三培优补差文科数学（三）1．已知集合{4,3,2,1,0,1,4}M =----，{3,2,1,0,1,2,3}N =---， 且M ，N 都是全集I 的子集，则图中阴影部分表示的集合为（ ） A ．{-1，-2，-3} B ．{0，1，2，3} C ．{2，3} D ．{0，-1，-2，-3} 2．i 是虚数单位，(3)i i -在复平面上对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知向量m ，n 的夹角为6π，且||3,||2,||m n m n ==-则=（ ） A ．4 B ．3 C ．2 D ．1 4．一个几何体的三视图如图所示，则该几何体的表面积等于（ ） A ．8π B ．9π C ．10π D ．11π5．函数()y f x =的图像如图所示，则函数12log ()y f x =的图像大致是 （ ）6．已知圆22:2440C x y x y +-+-=，直线:34140l x y -+=，则圆C 上的点到直线l 的距离最小值为（ ）A ．2B ．3C．5D ．77．阅读如图所示的程序框图，若输入5,6p q ==，则输出,a i 的值分别为（ ） A ．5,1a i == B ．5,2a i == C ．15,3a i == D ．30,6a i ==8．各项均为正数的等比数列{}n a 的公比2311,,,2q a a a 1≠成等差数列，则34262645a a a a a a a a ++=（ ） A ．512+ B ．512- C ．152- D ．512+ 9．已知直线:230m x y +-=，函数3cos y x x =+的图象与 直线l 相切于P 点，若l m ⊥，则P 点的坐标可能是（ ）A ．3(,)22ππ--B ．3(,)22ππ C ．3(,)22ππ D ．3(,)22ππ-- 10．定义在R 上的函数()y f x =是减函数，且对任意的a R ∈， 都有()()0f a f a -+=，若,x y 满足不等式22(2)(2)0f x x f y y -+-≤，则当14,2x x y ≤≤-时的最大值为（ ）A ．1B ．10C ．5D ．811．若命题“2,20x R ax ax ∀∈--≤”是真命题，则a 的取值范围是 。

2012届高三培优补差文科数学（四）一、选择题。

（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合{|1},{|22},A x x B x x A B =>-=-<<则=（ ）A ．{|2}x x >-B ．{|1}x x >-C ．{|21}x x -<<-D ．{|12}x x -<<2．i 是虚数单位，(1)i i += （ ）A ．1+iB ．-1-iC ．1-iD ．-1+i3．椭圆22413x y +=的离心率为（ ）AB ．34CD ．234．设,,OB xOA yOC x y R =+∈且A 、B 、C 三点共线（该直线不过点O ），则x+y=（ ）A ．-1B ．1C ．0D ．25．函数22cos ()14y x π=--是（ ）A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C ．最小正周期为2π的奇函数 D ．最小正周期为2π的偶函数 6．若圆222x 40x y y +--=的圆心到直线0x y a -+=的距离为2，则a 的值为（ ）A ．-2或2B ．2132或C ．20或D ．-2或07．实数x ，y 满足不等式组00220y x y x y ≥⎧⎪-≥⎨⎪--≤⎩，则11y w x -=+的取值范围是（ ）A ．1[1,]3-B ．11[,]23-C ．1,2⎡⎫+∞⎪⎢⎣⎭D ．1,12⎡⎫-⎪⎢⎣⎭8．给出下列四个命题：①若直线垂直于平面内的两条直线，则这条直线垂直于这个平面；②若直线与平面内的任意一条直线都垂直，则这条直线垂直于这个平面；③互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；④过点P 有且仅有一条直线与异面直线,l m 都垂直。

其中正确命题的个数有（ ）A ．0B ．1C ．2D ．39．设x ，y 为正数，且(1)(1)4,x y --=则（ ）A ．06x y <+≤B ．6x y +≥C ．1x y +≥+D ．01x y <+≤+10．已知定义在R 上的奇函数()f x 满足(4)()f x f x -=-，且在区间[0，2]上是增函数，则（ ） A ．(2)(5)(8)f f f << B ．(5)(8)(2)f f f <<C ．(5)(2)(8)f f f <<D ．(8)(2)(5)f f f <<二、填空题（本大题共5小题，每小题5分，共25分。

(第7题)安陆一中2012届高三数学选填题专题训练一一、选择题：本大题共10小题，每小题5分，共50分。

（1） 已知函数f（x ）＝267,0,100,,x x x x x ++<≥⎧⎪⎨⎪⎩则 f （0)＋f （-1)＝(A) 9 （B ）7110(C) 3 （D ）1110(2) “cos x ＝1”是“sin x ＝0”的(A ） 充分而不必要条件 (B ） 必要而不充分条件 （C ） 充分必要条件 (D ） 既不充分也不必要条件（3） 在等差数列｛a n }中，若a 2＋a 3＝4，a 4＋a 5＝6，则a 9＋a 10＝(A) 9 (B) 10 (C) 11 (D) 12(4） 设U 为全集,对集合X ,Y ，“*”，X *Y ＝(X ∩Y )．对X，Z, Y )*Z ＝（A) (X ∪Y ）∩ Z (B) （X ∩Y )∪ Z （C ） （ X ∪ Y ）∩Z (D ） （ X ∩ Y ）∪Z（5） 在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝2AB ．若E ，F分别为线段A 1D 1,CC 1的中点，则直线EF 与平面ABB 1A 1所成角的余弦值为（A ）3（B ）2(C)3(D ）13(6) 设F 是抛物线C 1：y 2＝2px （p的焦点，22221x y ab-=点A 是抛物线与双曲线C 2：（a ＞0,b ＞0）的一条渐近线的一个公共点，且AF ⊥x 轴，则双曲线的离心率为 (A ）2 （ (C)2(D （7） 运行后输出的S 的值为(A ） 1 （B ） 12(C ） 14(D ）18(8） 下列函数中，在(0,2π)上有零点的函数是(A ） f （x )＝sin x －x （B) f （x ）＝sin x －2πx（C) f （x )＝sin 2x －x (D) f (x ）＝sin 2x －2πx班级 姓名 分数（9）设,2,,2,x y x y z y x y -≥=<⎧⎨⎩若－2≤x ≤2，－2≤y ≤2，则z 的最小值为(A ）－4 (B)－2 (C ）－1 （D ） 0（10)设2010(12)(1)x x ++＝a 0＋a 1x ＋a 2x 2＋…＋a 10x 10＋29129100(1)b b x b x b x x +++++，则a 9＝(A) 0 (B) 410 （C) 10⋅410 (D) 90⋅410二、填空题: 本大题共5小题，每小题5分，共25分。

2012届高三数学第五次综合试题（文科）参考公式：球的表面积公式：24R S π= 棱柱的体积公式：sh V =球的体积公式：334R V π= 其中S 表示柱体的底面积，h 表示柱体的高其中R 表示球的半径台体的体积公式：)(312211S S S S h V ++=锥体体积公式：Sh V 31= 其中21,S S 分别表示棱台的上、下底面积，h 表示其中S 表示锥体的底面积，h 表示 棱台的高 锥体的高第I 卷(选择题 共50分)一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设全集=U R ，集合A =}1{>x x ，=B }032{2≥--x x x ，则()U A C B =I ( ) A ．}1{-≤x x B ．}1{≤x x C ．}11{≤<-x x D ．}31{<<x x 2．“α为锐角”是“0sin >α”成立的 ( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分又不必要条件3．设复数i z -=11，z 是z 的共轭复数，则=+z zA ．21i+ B ．i C ．1- D ．1 4．若变量y x,满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+04300y x y x y x ，则y x 23+的最大值是A ．0 B ．2C ．5D ．65．阅读右面的程序框图，则输出的S 等于A ．40 B ．38 C ．32 D ．206．某几何体的三视图如图所示，则该几何体的体积为( ) A ．6 B ．316 C ．314D ．4 7．非零向量a ，b 的夹角为 601=-( ) A ．41 B ．21C ．23D ．1（第5题） 正视图侧视图俯视图 （第6题）8．函数)(x f =)sin(ϕω+x ∈x (R ))20(πϕω<>,的部分图像如图所示，如果)3,6(,21ππ-∈x x ，且)()(21x f x f =，则=+)(21x x f ( ) A ．21B ．22C ．23D ．19．已知P 是椭圆)0(12222>>=+b a by a x 上的一动点，且P 与椭圆长轴两顶点连线的斜率之积为21-，则椭圆离心率为 ( )A ．23B ．22C ．21 D ．3310．已知函数x xe x f =)(，方程)(01)()(2R ∈=++t x tf x f 有四个实数根，则t 的取值范围为( )A ．),+∞+e e 1(2B ．)12(2e e +,C ．)2,1(2-+-e eD ．)1(2ee +--∞,第Ⅱ卷（非选择题，共100分）二、填空题（本大题共7小题，每小题5分，共35分）11．已知⎩⎨⎧≤+>=0)1(02)(x x f x x f x ，则)1(-f = ．12．已知直线23+=x y l :与圆:O 422=+y x相交于B A ,两点，则AB = ． 13．某班50名学生在一次健康体检中，身高全部介于155cm 与185cm 之间．其身高频率分布直方图如图所示．则该班级中身高在[]185,170之间的学生共有 人． 14．两个袋中各装有编号为1，2，3，4，5的5个小球，分别从每个袋中摸出一个小球，所得两球编号数之和小于5的概率为 ． 15．已知等比数列{}n a 的公比为2，前n 项和为n S ．记数列}{n b 的前n 项和为n T ，且满足12++=n n nn a a a b ，则n n T S = ．16．若不等式xy x y x a 2)2(222+≥+对任意非零实数y x ,恒成立，则实数a 的最小值为 ．17．如图，将菱形ABCD 沿对角线BD 折起，使得C 点至C '，（第13题）cm ）B（第17题） DAC 'EE 点在线段C A '上，若二面角E BD A --与二面角C BDE '--的大小分别为30°和45°，则CE AE'= ．三、解答题（本大题共5小题，共65分。