点线面专题复习课(9)
- 格式:ppt
- 大小:1.31 MB
- 文档页数:23



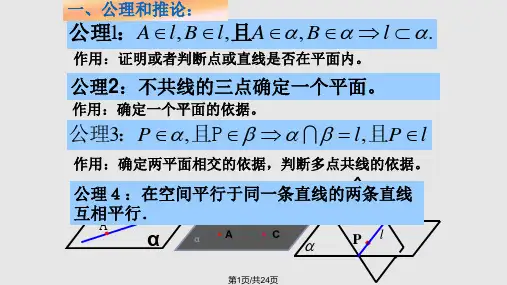
//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法(1)定义法:直线与平面无公共点。
(2)判定定理:(3)其他方法://a αββ⊂2.性质定理://a a bαβαβ⊂⋂=二、平面与平面平行 1.判定方法(1)定义法:两平面无公共点。
(2)判定定理:////a b a b a b Pββαα⊂⊂⋂= //αβ(3)其他方法:a a αβ⊥⊥ //αβ; ////a γβγ//αβ 2.性质定理://a bαβγαγβ⋂=⋂=三、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b ② 判定定理:a ba cb c A b c αα⊥⊥⋂=⊂⊂ a α⊥③ 推论://a a bα⊥ b α⊥ (3)性质 ①a b αα⊥⊂ a b ⊥ ②a b αα⊥⊥四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理a a αβ⊂⊥ αβ⊥ (3)性质①性质定理la a lαβαβα⊥⋂=⊂⊥ αβ⊥② l P P A A αβαβαβ⊥⋂=∈⊥垂足为 A l ∈④ l P PA αβαβαβ⊥⋂=∈⊥ PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角的平面角例1.如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC于D,交SC于E,又SA=AB,SB=BC,求以BD为棱,以BDE和BDC为面的二面角的度数。
●求线面夹角定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。


初中数学专题复习的“点线面”作者:王永恒来源:《新教育时代·教师版》2017年第41期摘要:在初中数学教学工作中,专题复习方面的内容较为重要,教师应当予以足够重视,合理使用“点线面”专题复习方式开展教学工作,以便于培养学生数学知识掌握能力,使其在复习期间,明确重点内容,养成良好的学习习惯,根据中考重点与难点内容等,对各类知识进行复习。
关键词:初中数学专题复习“点线面”初中数学专题复习“点线面”教学方式,主要是教师建立专门的知识模块,在相互关联的情况下,构建先进的结构图,培养学生的数学知识学习能力,在数形结合思想的指导下,自主探究知识,掌握数学内容。
一、遵循以“面”理“线”的教学原则初中数学复习中的专题内容较多,在不同书籍与资料中,会罗列大量的学习内容,在教学期间,教师不能对其进行照搬照抄的讲解,而是根据学生学习特点与需求,制定完善的规划方案,同时,要明确当地中考内容的重点与难点,明确学生基本技能的培养要求,筛选最佳方式,对专题教学问题进行设计,以此提升工作效率,在遵循利导与梳理原则的情况下,提升工作效果。
例如:某地区在2015年中考期间,重点内容为“圆中角度转换结合相似求面积”、“单参抛物线中求点坐标”。
在2016年,中考重点内容为“圆中证角等求角度”、“单参抛物线三角形面积”等。
因此,教师要根据历年中考中重点问题开展设计工作,保证在实际教学期间,结合学生的年龄特点与学习现状,对各类教学内容进行设计,将最值、存在性、运动、函数与几何等综合问题融入专题训练中,以便于开展相关管理工作。
例如:在学生复习最值专题内容的过程中,不能综合考虑各类数学问题,因此,教师在安排专题复习项目的过程中,可以将此类问题融入学生学习内容,以便于开展管理工作。
二、遵循以串“珠”成“链”的教学原则在初中数学专题复习工作中,教师应当保证专题复习内容的科学性与精细化,在合理选择专题内容的基础上,提高教学效率,构建现代化复习教学方案。



高考专题复习:化学中的点、线、面中学化学中的空间想象能力主要是指以观察物质结构的实物模型、空间图式为基础,用三维的、运动的观点对物质的空间结构进行模拟、剖析、综合和计算的能力。
它是近几来高考的重点内容之一。
它主要包括三个方面的问题:①常见物质的键角与分子构型的关系,②晶体结构,③有机物分子共线、共面的问题。
二、晶胞中粒子数的计算方法1、概念:在晶体结构中具有代表性的最小的重复单位称为晶胞。
晶胞在三维空间无限地重复就产生了宏观的晶体,可以说,晶体的性质是由晶胞的大小、形状和质点的种类(分子、原子或离子)以及它们之间的作用力所决定的。
由晶胞构成的晶体其化学式不是表示一个分子中含有多少个原子,而是表示每个晶胞中平均含有各类原子的个数,即各类原子的最简个数比(气态团簇分子除外!)2、晶胞中实际拥有粒子数的计算规则:(1)处于晶胞顶点上的粒子,同时为8个晶胞所共有,每个粒子只有1/8属于该晶胞;(2)处于晶胞棱上的粒子,同时为4个晶胞所共有,每个粒子只有1/4属于该晶胞;(3)处于晶胞面上的粒子,同时为2个晶胞所共有,每个粒子只有1/2属于该晶胞;(4)处于晶胞内部的粒子,完全属于该晶胞。
三、有机物分子共线、共面的问题原子共面共线问题思维的基础:其一是甲烷的正四面体结构;乙烯、苯、萘、蒽的平面结构;乙炔的直线结构,其二是碳碳单键可以旋转,而双键和叁键则不能旋转。
1、烷的正四面体结构在甲烷分子中,一个碳原子和任意两个氢原子可确定一个平面,图1 甲烷的分子结构模型其余两个氢原子分别位于平面的两侧,即甲烷分子中有且只有三原子共面(称为三角形规则)。
当甲烷分子中某氢原子被其他原子或原子团取代时,该代替原子的共面问题,可将它看作是原来氢原子位置。
323CH CH CH 其结构式可写成如图2所示。
左侧甲基和②C 构成“甲烷分子。
此分子中⑤H ,①C ,②C 构成三角形。
中间亚甲基和①C ,③C 构成“甲烷”分子,此分子中①C ,②C ,③C 构成三角形,同理②C ,③C ,④H 构成三角形,即丙烷分子中最多三个碳原子(①C ,②C ,③C)二个氢原子(④H ,⑤H)五原子可能共面。

必修2 点线面复习姓名一、点线面的关系:直线和直线有3种关系:相交、平行、异面;直线和平面有3种关系:相交、平行、在平面内;平面和平面有2种关系:相交、平行;二、平行垂直的判定:线面平行:线平行面内一条直线————线线平行面面平行:相交直线平行面——————线线平行×2线面垂直:线垂直面内两条相交直线——线线垂直×2面面垂直:过面的垂线————————线线垂直×2三、平行垂直的性质:线面平行:线与交线平行面面平行:面面交线平行线面垂直:(1)线垂直于面内任何一直线(2)两垂线平行面面垂直:垂直交线的垂直面典型例题:1、如图,在三棱锥A-BCD中,E、F是棱AB、AD的中点求证:EF∥平面BCD2、在正方体ABCD-A 1B1C1D1中,E为边DD1的中点,O为AC和BD的交点,求证:BD1∥平面AEC3、三棱锥A-BCD中,E、F、G分别是AB、AD、AC的中点求证:平面EFG∥平面BCD4、在正方体ABCD-A1B1C1D1中,E、F为A1D1和BC的中点求证:EF∥平面ABB1A15、三棱锥A-BCD中,AB=1,AD=2,求证:AB⊥平面BCD6、三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD求证:CD⊥平面ABC7、在四棱锥S-ABCD中,SD⊥平面ABCD,底面ABCD是正方形求证:AC⊥平面SBD8、ABCD和DCCD1是两个正方形,平面ABCD⊥平面DCC1D1(1)求证:AD⊥平面DCC1D1(2)求证:D1D⊥平面ABCD(3)CD⊥平面BCC1(4)AC⊥平面BDD19:、(湖北文)如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,点E是线段SD上的任意一点,求证: AC⊥BE10、(江西文)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,M 为PD 上一点,求证:平面ABM ⊥平面A P D11、(10广州一模)如图,正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ,AE ⊥平面CDE ,求证:AB ⊥平面ADE ;12、在四面体ABCD 中,CB=CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点, 求证(I )直线EF D 平面AC ;(II )EFC D ⊥平面平面BC 。
