张量分析答案完整版
- 格式:pdf
- 大小:480.91 KB
- 文档页数:40

一 爱因斯坦求和约定1.1指标变量的集合:n n y y y x x x ,...,,,...,,2121表示为:n j y n i x j i ...,3,2,1,,...,3,2,1,==写在字符右下角的 指标,例如xi 中的i 称为下标。
写在字符右上角的指标,例如yj 中的j 称为上标;使用上标或下标的涵义是不同的。
用作下标或上标的拉丁字母或希腊字母,除非作了说明,一般取从1到n 的所有整数,其中n 称为指标的范围。
1.2求和约定若在一项中,同一个指标字母在上标和下标中重复出现,则表示要对这个指标遍历其范围1,2,3,…n 求和。
这是一个约定,称为求和约定。
例如:333323213123232221211313212111bx A x A x A b x A x A x A bx A x A x A =++=++=++筒写为:ijijbx A =j——哑指标i——自由指标,在每一项中只出现一次,一个公式中必须相同遍历指标的范围求和的重复指标称为“哑标”或“伪标”。
不求和的指标称为自由指标。
1.3 Kronecker-δ符号(克罗内克符号)和置换符号Kronecker-δ符号定义j i ji ij ji ≠=⎩⎨⎧==当当01δδ置换符号ijkijk e e =定义为:⎪⎩⎪⎨⎧-==的任意二个指标任意k j,i,当021)(213,132,3的奇置换3,2,1是k j,i,当112)(123,231,3的偶置换3,2,1是k j,i,当1ijk ijke ei,j,k 的这些排列分别叫做循环排列、逆循环排列和非循环排列。
置换符号主要可用来展开三阶行列式:231231331221233211231231133221332211333231232221131211a a a a a a a a a a a a a a a a a a a a a a a a a a a a ---++==因此有:ijmjimii i i jijAA aa a a a ==++=δδδδδ332211kijjkiijkkjiikjjikijkee e e e e e ==-=-=-=同时有:ijjijij iiiijijijkj ikilkljkijjjiiijijijkjikiie e aa aa a a a aa δδδδδδδδδδδδδδδδδδδ=⋅=++=========++=332211332211331001010100131211232221333231321333222111321321321-=====δδδδδδδδδδδδδδδδδδδδδδδδδδδe e k j i k j i k j i k k k j j j i i i ijk333222111321321321r q p r q p r q p k k k j j j i i i pqr ijke e δδδδδδδδδδδδδδδδδδ⋅=ipp i p i p i p i δδδδδδδδδ==++11332211krkqkpjrjqjpiriqippqrijke e δδδδδδδδδ=jqirjriqjrjqiriqkqrijke e kp δδδδδδδδ-===321321322311332112312213322113312312332211333231232221131211k j i ijkkjiijkaa a e a a a e aa a a a a a a a a a a a a a a a a aaaa a aaa a A ==---++==Kronecker-δ和置换符号符号的关系为:itjsjtiskstkije e δδδδ-=二 张量代数2.1张量的加法(减法)两个同阶、同变异(结构) 的张量可以相加(或相减)。


《连续介质力学》例题和习题第一张、矢量和张量分析第一节 矢量与张量代数一、 矢量代数令 11223A A A =++A e e e 112233B B B =++B e e e 则有 11223A A A αααα=++A e e e 11122233()()()A B A B A B +=+++++A B e ee 1122331122331122()()A A A B B B A B A B A B ∙=++∙++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e 又因为 11⨯=e e 0 123⨯=e e e 132⨯=-e e e 213⨯=-e e e 22⨯=e e 0 231⨯=e e e 312⨯=e e e 321⨯=-e e e 33⨯=e e 0则 2332131132122(_)()()A B A B A B A B A B A B⨯=+-+-A B e e e习题1、证明下列恒等式:1)[]2()()()()⨯∙⨯⨯⨯=∙⨯A B B C C A A B C2) [][]()()()()⨯∙⨯=∙⨯-∙⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关?1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 单位为正交的基矢量。
*补充知识:矩阵及矩阵运算1、定义:[]()111213212223313233,1,2,3ij A A A A A A A i j A AA ⎡⎤⎢⎥⎡⎤===⎣⎦⎢⎥⎢⎥⎣⎦A i 表示行,j 表示列;m 和n 相等表示为方阵,称为m (或n )阶矩阵。





第二章 正交曲线坐标系下的张量分析与场论1、用不同于书上的方法求柱坐标系和球坐标系的拉梅系数及两坐标间的转换关系ij β。
解:①柱坐标系k z j i r++=ϕρϕρs i n c o s ,2222222dz H d H d H ds z ++=ϕρϕρ ()()k dz j d d i d d r d+++-=ϕϕρρϕϕϕρρϕcos sin sin cos()()222222222222222222222222222222c o s s i n s i n c o s c o s s i n 2c o s s i n s i n c o s s i n 2c o s c o s s i n s i n c o s dz d d dz d d d d dz d d d d d d d d dz d d d d r d r d ds ++=++++=+++++-=+++-=⋅=ϕρρϕϕρϕϕρρϕρϕϕρϕϕρϕϕρρϕϕϕρϕρϕϕρρϕϕϕρρϕϕϕρρϕ故:1=ρH ,ρϕ=H ,1=z H ②球坐标系k R j R i R r θφθφθc o s s i n s i n c o s s i n ++=,2222222φθφθd H d H dR H ds R ++=()()()kd R dR j d R d R dR id R d R dR r dθθθφφθθφθφθφφθθφθφθsin cos cos sin sin cos sin sin sin sin cos cos cos sin -++++-+= ()()()2222222222s i n s i n c o s c o s s i n s i n c o s s i n s i ns i n s i n c o s c o s c o s s i n φθθθθθφφθθφθφθφφθθφθφθd R d R dR d R dR d R d R dR d R d R dR r d r d ds ++=-++++-+=⋅=故:1=R H ,R H =θ,θφsin R H = ③两坐标间的转换关系ij βφr re e θe φPθru re e zu ze r(1)圆柱坐标系 (2)球坐标系由球坐标系与直角坐标系的坐标变换矩阵为:sin cos sin sin cos cos cos cos sin sin sin cos 0r e i e j e k θφθφθφθθφθφθφφ⎧⎫⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥=-⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥-⎣⎦⎩⎭⎩⎭注意,圆柱坐标系中的θ和球坐标系的φ相等。

张量分析作业1.2题 证明:()()()()()()()()()()()()()()()()()()()()()()()()()C B AD D B A C D C B A U B A D C B A D C A B U B A U A B B A U A B U BA U AB U B A U B A DC wv u v w u w v u U D C B A D C D C B A ⨯∙-⨯∙=⨯⨯⨯=⨯⨯∙-⨯∙=∙-∙=∙+∙-∙+∙-=⨯⨯-=⨯⨯⨯-∙-∙=⨯⨯=⨯⨯⨯⨯-=⨯⨯⨯令同理可证得:利用点积交换律得:得:,利用公式设1.5 求证:0a b ⨯=⇔,a b 线性相关。
证明: a b ⨯=xy z xy zij ka a ab b b =()()()0y z z y z x x z x y y x a b a b i a b a b j a b a b k -+-+-= ∴i j j i a b a b =即i ji ja a kb b == i i a kb = i j k i j k k k k a i a j a k b i b j b k ∴++=++即k =a b ,a b ∴线性相关 同理可证 当,a b 线性相关时,0a b ⨯= ∴0a b ⨯=⇔,a b 线性相关。
1-7解:c mb a =+ ()1,2,3c =()2,,2mb m m m =- (),,a x y z =22021223x y z m x m y z m +-=+=+=-=解得1320234,,,9999x y z m ====-132023999a i j k =++1.8 试求线元d kx 的长度d k s 。
解:d d d d =d d d k ki k k ki i i x g x x x g r g r r δ=⇒==⇒1.10、解:(1)由公式g 1=g1(g 2×g 3)g 2=g 1(g 3×g 1)g 3=g1(g 1×g 2)又g =[g 1 g 2 g 3]=k ×i ·j ,得g 1=j i k jk i k j i ∙⨯⨯+⨯+⨯g 2=j i k kj k i j i ∙⨯⨯+⨯+⨯g 3=ji k jk k i j i ∙⨯⨯+⨯+⨯(2)g rs =323121g g g g g g g g s r ∙+∙+∙=⨯=()()()()()()j i k i j i k j k i k j +∙+++∙+++∙+ =222j k i ++1-10、解:(1)由公式g 1=g1(g 2×g 3)g 2=g 1(g 3×g 1)g 3=g1(g 1×g 2)又g =[g 1 g 2 g 3]=k ×i ·j ,得g 1=j i k jk i k j i ∙⨯⨯+⨯+⨯g 2=j i k kj k i j i ∙⨯⨯+⨯+⨯g 3=ji k jk k i j i ∙⨯⨯+⨯+⨯(2)g rs =323121g g g g g g g g s r ∙+∙+∙=⨯=()()()()()()j i k i j i k j k i k j +∙+++∙+++∙+ =222j k i ++1.17求:题1.13所示圆柱坐标和球坐标i x ,与笛卡尔坐标j x '的转换系数'i j β与'j i β。

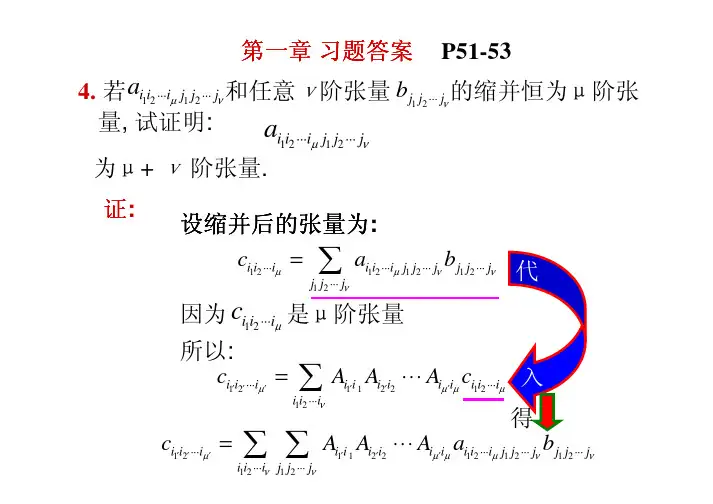
练习题Ⅱ(金属所)1. 用下标符号证明:C B A B C A C B A )()()(⋅-⋅=⨯⨯。
2. 证明nknj ni mk mj mi lklj li lmn ijk δδδδδδδδδ=∈∈3. 证明ijk klm =(δil δjm -δim δjl )4. 证明ijk ikj =-6。
5. 证明ijkmik =-2δjm 。
6. 证明具有中心对称的晶体不具有由奇阶张量描述的物理性质,但由偶阶张量描述的物理性质也具有中心对称的特性。
7. B 为矢量,M 为二阶张量,证明:(div M )⋅B =div(M ⋅B )-{ (B ∇)∶M } 8. 设在P 点的应力张量 σ如下:求法线方向为]221[的面上的正应力。
⎪⎪⎪⎭⎫ ⎝⎛----=211121112)(ij σ9. 设在P 点的应力张量 σ如下:求该处的主应力及主方向。
并验证主方向是相互正交的。
⎪⎪⎪⎭⎫ ⎝⎛=740473037)(ij σ10. 位移场u 在给定坐标系下的分量分别是:u 1= ax 2+bx 3,u 2=ax 1cx 3,u 3= bx 2+cx 3;其中a 、b 、c 皆为常数。
求这个位移场的应变张量Γ。
11. 弹性体的的应变张量场如下所示,这个应变张量场合理吗?⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=32222111216112226226)(x x x x x x x ij ε12. 在立方晶体中承受一均匀应力场,以]101[、]211[和[111]为x 1、x 2和x 3坐标轴的应力分量只有σ13和σ23两项,求以三个晶轴作坐标系的各应力分量σ’ij 。
练习题Ⅱ解答(金属所)1. 用下标符号证明: C B A B C A C B A )()()(⋅-⋅=⨯⨯。
解:CB A BC A e e e e e C B C B A )()()(()()()(⋅-⋅=-==∈∈=∈=∈⨯=∈⨯⨯i i j j j i j i jl im jm il m l j i klm ijk m l j ik m l klm j ijk i k j ijk c b a c b a )δ-δδδc b a c b a c b a a 2. 证明nknj ni mk mj mi lklj li lmn ijk δδδδδδδδδ=∈∈解:a ij 的行列式为333231232221131211det a a a a a a a a a A = 当行列式行与行、列与列对换一次行列式的值就变号一次,任意换行后有A a a a a a a a a a lmn n n n m m m l l l det 321321321=∈ 任意换列后有A a a a a a a a a a ijk kjik j i kj i det 333222111=∈ 因此,任意行与行、列与列交换后有A a a a a a a a a a lmn ijk nkmkninj mj mi nimi li det ∈=∈ 令a ij =δij ,det A =1,则有lmn ijk nknj ni mk mj mi lklj li ∈=∈δδδδδδδδδ 3. 证明ijk klm =(δil δjm -δim δjl ) 解:根据上题的结果,有)()3()3()()(im jl mj li li mj mj li mi lj mj li mi lj jl im li kj mk ki mj lk mi lj kk mj li kk mi lk kj mk lj ki mkmj mi lklj li kkkj ki klm ijk δδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδδ-=++-++=++-++==∈∈4. 证明ijk ikj =-6解:ijk ikj =-ijk kij =-(δii δjj -δij δji )=-(33-δii )=-(9-3)=-65. 证明ijk mik =-2δjm解:ijk mik =ijk kmi =(δim δji -δii δjm )= (δjm -3δjm )=-2δjm6.证明具有中心对称的晶体不具有由奇阶张量描述的物理性质,但由偶阶张量描述的物理性质也具有中心对称的特性。
2.9克里斯托弗尔符号 ij i g j gkk ig j gkrgr gkr ig j g r gkr ijr(2.9.08) (2.9.09)同样地, ijk g kr ijr在基矢量组 g 1 , g 2 , g 3 中把 i g j 按下式分解 igj(4)在直线坐标系中, ijk 0 , ij 0k(2.9.10)k ij ijp gp ij g pp(2.9.01) (2.9.02)p ij事实上,因为在斜角和直角坐标系中基矢量 i i 和 e i 均为常量,故 ijk 0 和 (5)克里斯托弗尔符号可用度量张量表示。
事实上,由于g ij , k gk 0。
ig j 这里分解系数 ijp 和 分别称为第一类和第二类克里斯托弗尔(Christoffel)符号。
在某些文献中, p 第一类和第二类克里斯托弗尔符号分别用 ij , p 和 表示。
ij gigj kgi gj g i k gj kij kji(2.9.11) (2.9.12) (2.9.13)对指标进行轮换,则有jk , i ijk ikj用 g k 和 g 分别点乘式(2.9.01)和式(2.9.02)两边,则得 ijp gpkg ki , j jki jik把式(2.9.12)和式(2.9.13)相加,再减去式(2.9.11),则得 (2.9.03) (2.9.04) 另外, ijk 1 2 g k ijp kp k ijk i g j g kk ij ig j ggkrjk , i g ki , j gji , k(2.9.14)现述克里斯托弗尔符号的性质如下。
补充知识:张量分析1. 指标符号
2.矢量的基本运算
3.坐标变换与张量定义
4.张量的代数运算(1).加减法
(2).矢量与张量的点积(点乘)
(3).矢量与张量的叉积
(4).两个张量的点积
(5).张量的双点积
(6).张量的双叉乘
(7).张量的缩并
(8).指标置换
和(9).对称化和反对称化
5.二阶张量(仿射量)概述
(1).张量的转置B T
(2).张量的逆B-1
(3).对称仿射量的主向和主值
(4).各向同性张量
6.张量分析
概述
(1).哈密尔顿算子(梯度算子)
(2).张量场的微分
(3).散度定理
7.曲线坐标系下的张量分析(1).曲线坐标
(2).局部基矢量
(3).张量对曲线坐标的导数
END。