当前位置：文档之家 › FFT离散傅氏变换的快速算法

FFT离散傅氏变换的快速算法

  • 格式：docx
  • 大小：11.61 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

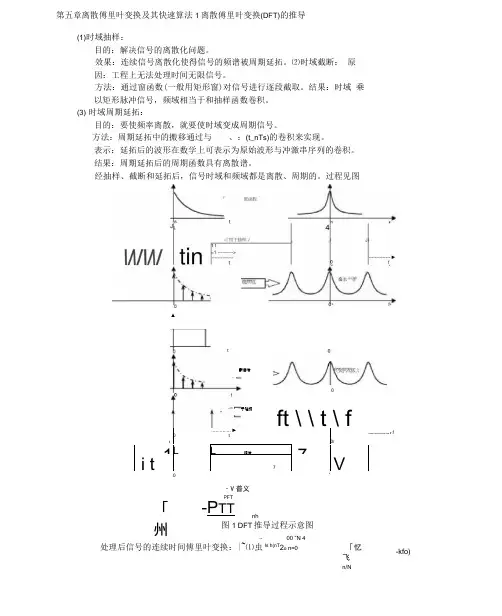
[理学]离散傅里叶变换及其快速算法

[理学]离散傅里叶变换及其快速算法

可先使信号通过一个低通滤波器使滤波后的信号中的最高频率成为fmax然后根据采样定理来确定采样频率f2称为nyquist频率或称混叠频率离散傅里叶变换的泄漏问题leakage在实际应用中通常将所观测的信号限制在一定的时间间隔内也就是说在时域对信号进行截断操作或称作加时间窗亦即用时间窗函数乘以信号即由卷积定理可知时域相乘频域为卷积则有有时会造成能量分散现象称之为频谱泄漏频谱泄漏
非周期序列的离散时间傅里叶变换 (DTFT) /序列的傅里叶变换
• 定义序列x(n)的离散时间傅里叶变换(DTFT)为：
X (e ) DTFT{x(n)}
j n jn x ( n )e
• 序列x(n)的离散时间傅里叶逆变换(IDTFT)为：
x(n) IDTFT{X (e j )} 1 2
按时间抽取的FFT算法
• 设N=2M，M为正整数，如取N=23=8，即离散时间信号为
x(n) {x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7)}
• 按照规则①将序列x(n)分为奇偶两组，一组序号为偶数， 另一组序号为奇数，即
{x(0), x(2), x(4), x(6) | x(1), x(3), x(5), x(7)}



X (e j )e jn d
傅里叶变换对小结
• 傅里叶级数(FS)（时域：连续周期；频域：非周期离散）
1 Xk T

T 2
T 2
x(t )e jk1t dt
x(t )
k


X k e jk1t
k 0, 1, 2,
• 傅里叶变换(FT)（时域：连续非周期；频域：非周期连续）
第三章-离散傅里叶变换(DFT)及其快速算法(FFT)

第三章-离散傅里叶变换(DFT)及其快速算法(FFT)

返回
• 序列x(n)的N点DFT是 x(n)的Z变换在单位圆上的N点等 间隔采样；
• X(k)为x(n)的傅立叶变换 X (e j ) 在区间 [0, 2 ]上的N
点等间隔采样。这就是DFT的物理意义。
j ImZ
2 3
4
5 6
1 2
N
k=0 ReZ
7 (N-1)
DFT与z变换
X(ejω)
)
N M
xN (n) x((n))N X (k ) X ((k ))N
有限长序列x(n)的DFT变换X(k)，就是x(n)的周期延拓序列 ~x(n) 的DFS系数 X~(k ) 的主值序列
返回
回到本节
DFS与FT之间的关系:
M 1
X (k) DFS[xN (n)] x(n)WNkn n0
x(n)
IDFT[ X (k)]N

1 N
N 1
X (k)WNk n ,
k 0
n 0, 1,
, N 1
长度为 N的离 散序列
返回回Biblioteka 本节例3.1： x(n) R8(n)，分别计算x(n)的8点、16点DFT。 解: x(n)的8点DFT为
X (k)

7 n0
R8 (n)W8k n
k 0,1, , N 1
n0
返回
回到本节
比较前面三式，得到
X (k) X (z) j2k ，k=0, 1, 2, …, N-1 ze N
X (k) X (ej ) 2k ，k=0, 1, 2, …, N-1 N
结论： (1)序列的N点DFT是序列傅里叶变换在频率区间[0，2] 上的N点等间隔采样，采样间隔为2 /N。 (2)序列的N点DFT是序列的Z变换在单位圆上的N点等间隔 采样，频率采样间隔为2 /N。
FFT-快速傅里叶变换

FFT-快速傅里叶变换

pi[0]=0.0;
p=6.283185306/n;
pr[1]=cos(p);
pi[1]=-sin(p);
if (l)
pi[1]=-pi[1];
for(i=2;i<=n-1;i++){
p=pr[i-1]*pr[1];
q=pi[i-1]*pi[1];
s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);
注：亲测，这个版本无法运行，作者删改了重要内容[1] 请参考源码（2）
//快速傅立叶变换
// 入口参数：
// l: l=0, 傅立叶变换;l=1, 逆傅立叶变换
// il: il=0,不计算傅立叶变换或逆变换模和幅角；il=1,计算模和幅角
// n: 输入的点数，为偶数，一般为32，64，128，...,1024等
wi = wi*wpr + wtemp*wpi + wi;
}
mmax = istep;
}
}
在C++环境下的源码
bool FFT(complex<double> * TD, complex<double> * FD, int r)
{
//一维快速Fourier变换。
//complex<double> * TD ——指向时域数组的指针; complex<double> * FD ——指向频域数组的指针; r ——2的幂数，即迭代次数
// fr[]: l=0, 返回傅立叶变换的实部
// l=1, 返回逆傅立叶变换的实部
// fi[]: l=0, 返回傅立叶变换的虚部
离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法

第五章离散傅里叶变换及其快速算法1离散傅里叶变换(DFT)的推导(1)时域抽样：目的：解决信号的离散化问题。

效果：连续信号离散化使得信号的频谱被周期延拓。

⑵时域截断： 原因：工程上无法处理时间无限信号。

方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。

结果：时域 乘以矩形脉冲信号，频域相当于和抽样函数卷积。

(3) 时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。

方法：周期延拓中的搬移通过与 、：(t_nTs)的卷积来实现。

表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。

结果：周期延拓后的周期函数具有离散谱。

经抽样、截断和延拓后，信号时域和频域都是离散、周期的。

过程见图▲t載曲后ft \ \ t \ f.............. ►t---------------- r fi0/1LL紹后-7ii t7V亍延拓・V 普义PFT「州-P TTnh图1 DFT 推导过程示意图〜00 ”N 4处理后信号的连续时间傅里叶变换：|~⑴虫ls h(nT 2o n=0「忆飞n/N-kfo)(i)l~(f)是离散函数，仅在离散频率点f 二kf 。

k —处存在冲激，强度为a k ，其To NTs余各点为0。

〜 N N 1(ii) H(f)是周期函数，周期为Nfo == I ，每个周期内有N 个不同的幅值。

To NTs Ts(iii)时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。

2 DFT 及IDFT 的定义(1) DFT 定义：设hnTs 是连续函数h(t)的N 个抽样值J ，这N 个点的宽度为N 的 DFT 为:DFT N h(nTs)]=A h(nTs)ej 2ffi /N =H ——J (k =0,1,..., N_1)7l NT s 丿IDFT 定义：设H 上是连续频率函数吧的N 个抽样值k 亠，…• N J ，这N 个点(NTs 丿 的宽度为N的IDFT 为：DFTN 1Hk_L7HLe 「2「伙/N 厶 门Ts,(k=0,1,…，N —1)|L NsN k 卫 NTs“Rk/N 称为N 点DFT 的变换核函数，龊讪称为N 点IDFT 的变换核函数。

第三章离散傅里叶变换及其快速计算方法(DFT、FFT)

第三章离散傅里叶变换及其快速计算方法(DFT、FFT)


X (e jw )
（2）Z 变换 -- 提供任意序列的 z 域表示。
n

x( n)e jnw
X (z)
n


x ( n) z n
这两种变换有两个共同特征：
（1）变换适合于无限长序列 （2）它们是连续变量 ω 或 z 的函数
华北电力大学自动化系
3
3.1 问题的提出：可计算性
X (z)
而对于
n


x ( n) z n
n


x ( n) z n
找不到衰减因子使它绝对可和（收敛）。为此，定义新函 数，其 Z 变换：
华北电力大学自动化系
15
DFS 定义：正变换
X ( z)
n
x ( n) z n ~ ( n ) z n x
华北电力大学自动化系
6
3.1 问题的提出：傅里叶变换的四种形式 （3）
2. 周期连续时间信号：傅里叶级数 FS
~ (t ) x X (n 0 )
t T

时域周期频域离散
0
2 T
x(t)
~
n -
X(n 0 )e jn0t

时域连续函数造成频域是非周期的谱。 频域的离散对应时域是周期函数。
X (e jT )



T T
X (e jT )e jnT d
取样定理
n

x(nT )e jnT
1 X ( 0 ) T n
时域的离散化造成频域的周期延拓 时域的非周期对应于频域的连续
华北电力大学自动化系
8
第2章 离散傅里叶变换(DFT)及其快速算法(FFT)

第2章 离散傅里叶变换(DFT)及其快速算法(FFT)


电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
信号特性的时频域对应关系 连续 离散 周期
非周期 周期 离散
电信系信息技术教研室
2.1.1 离散傅里叶级数DFS
？如何对周期为N的周期序列进行频域分析……
如： ~(n) ~(n kN ) x x 周期序列不能进行Z变换，因为其在 n=-到+ 都 周而复始永不衰减，即 z 平面上没有收敛域，所以 其DTFT亦不存在。但是，如同连续时间周期信号可用 傅氏级数表达，周期序列也可用离散的傅氏级数来表 示。

2 1 2 1

X (2) 0 X (6) 0
X (3) 1 j X (7 ) 1 j

2 1 2 1

电信系信息技术教研室
解法二：公式解
N 1 j 2 N 7 j 2 8 kn
X
k
DFS x n
mk
ki mk ~ ~ x (i ) wN wN X ( k ) i 0
N 1
电信系信息技术教研室
3）共轭对称性
x 对于复序列 ~n ，其共轭序列为
~* ~* DFS x n X k
* *
~* x n
，则：
~ ~ DFSx n X k
解：上述序列的基本周期为 N=4，因而
W4 = e-j2π /4 = -j，
~ X (k )
~ X (0) ~ X (1 ) ~ X (2) ~ X (3)

n0
3
nk ~ x ( n )W 4
3

n0
3
~ ( n )W x 4
FFT是离散傅立叶变换的快速算法

FFT是离散傅立叶变换的快速算法

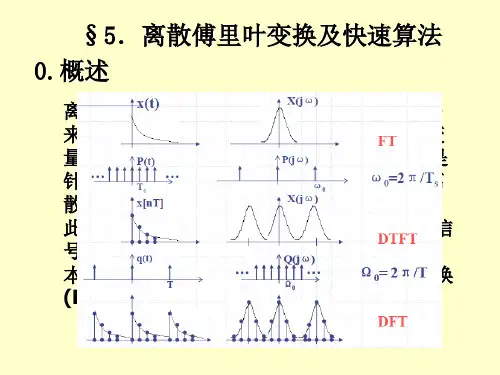
FFT是离散傅立叶变换的快速算法离散傅立叶变换（Discrete Fourier Transform, DFT）是一种将离散信号变换到频域的方法，它在数字信号处理中有着广泛的应用。

然而，传统的DFT算法的计算复杂度为O(N^2)，对于大规模的信号序列而言，计算时间会很长。

为了解决这个问题，FFt算法应运而生。

快速傅立叶变换（Fast Fourier Transform, FFT）是一种通过分治思想将DFT算法转化成更高效的计算方式。

FFT算法的核心思想是将一个长度为N的信号分解成N个长度为1的信号，然后逐步合并计算每个信号的频域表示，最终得到整个信号的频域表示。

FFT算法的时间复杂度为O(NlogN)，大大提高了计算效率。

FFT算法的基本思想是基于蝶形运算和旋转因子的运用。

蝶形运算是指将两个频域采样值进行乘法和加法操作，然后得到两个新的频域采样值。

旋转因子是指用来调整频域采样的运算公式，可以通过旋转因子将频域采样值分解成两个较小规模的频域采样值。

通过不断地重复蝶形运算和旋转因子的运算，最终可以得到整个信号的频域表示。

在FFT算法中，需要注意的是将信号序列长度N转化为2的幂次方，这是因为FFT算法要求信号序列的长度必须是2的幂次方。

如果信号序列的长度不是2的幂次方，需要进行长度的补齐或者截断操作。

通过对信号序列进行补齐或者截断，可以避免频谱泄漏的问题，并且可以确保FFT算法的正确性。

FFT算法的具体实现通常采用递归或者迭代的方式。

递归实现的FFT算法主要是通过将整个信号序列分解成较小规模的子序列，然后对每个子序列进行FFT计算，最终得到整个信号的频域表示。

迭代实现的FFT算法则是通过依次计算每个蝶形运算的结果，从而得到整个信号的频域表示。

FFT算法在数字信号处理领域有着广泛的应用。

例如，它可以用于信号的滤波和去噪、信号的频谱分析和频率成分提取、图像处理中的边缘检测和特征提取等。

由于FFT算法具有高效的计算速度，尤其适合处理大规模信号序列，因此在实际应用中被广泛采用。

离散傅里叶变换及快速算法

离散傅里叶变换及快速算法


（5-5）
W e N
j
2 N
的性质:
正交性，周期性，
共轭对称性（偶序列），可约性。
§5．离散傅里叶变换及快速算法
1.离散傅里叶级数
1.2离散傅里叶级的计算
例5-1 求出下面周期序列的DFS
x(n) 0 ,1,2,3, 0 ,1,2,3, 0,1,2,3
n0
为改进嵌套循环计算的效率，将循环结构改为矩阵形式计算
§5．离散傅里叶变换及快速算法
0.概述
离散时间傅里叶变换(DTFT)是通过周期频谱 来描述一个离散信号序列，即DTFT是连续变 量w的连续函数。离散傅里叶变换(DFT)则是 针对有限长序列，是对DTFT采样后得到的离 散序列。 此种表示方法非常有利于数值计算以及数字信 号处理算法的DSP硬件实现。 本章将研究离散傅里叶级数，离散傅里叶变换 (DFT)，及离散傅里叶变换的快速算法FFT。
（5-3）
n0
称之为离散傅里叶级数DFS的系数。是一个基波周期为N的 周期序列。
X (k) X (k N)
§5．离散傅里叶变换及快速算法
W e 在DFS变换中引入复数 N
j
2 N
将DFS正反变换描述为
N 1
X (k) x(n)WNnk
n0
x (n)
1 N
N 1
X (k )WNnk
k 0
n0
x(n)
1 N
N 1
X (k )WNnk
k 0
x
1 N
WN* X
WN WNkn 0
k,n
N
1
1 1
1
WN1
1
W ( N 1) N
1
W ( N 1) N
DFT算法原理、FFT的算法原理

DFT算法原理、FFT的算法原理

DFT 算法原理快速傅氏变换（FFT ）是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。

设x(n)为N 项的复数序列，由DFT 变换，任一X （m ）的计算都需要N 次复数乘法和N-1次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出N 项复数序列的X （m ）,即N 点DFT 变换大约就需要N2次运算。

当N=1024点甚至更多的时候，需要N2=1048576次运算，在FFT 中，利用WN 的周期性和对称性，把一个N 项序列（设N=2k,k 为正整数），分为两个N/2项的子序列，每个N/2点DFT 变换需要（N/2）2次运算，再用N 次运算把两个N/2点的DFT 变换组合成一个N 点的DFT 变换。

这样变换以后，总的运算次数就变成N+2（N/2）2=N+N2/2。

继续上面的例子，N=1024时，总的运算次数就变成了525312次，节省了大约50%的运算量。

而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的DFT 运算单元，那么N 点的DFT 变换就只需要Nlog2N 次的运算，N 在1024点时，运算量仅有10240次，是先前的直接算法的1%，点数越多，运算量的节约就越大，这就是FFT 的优越性。

、FFT的算法原理FFT 算法的输出X(K)为自然顺序，但为了适应原位计算，其输入序列不是按x(n)的自然顺序排序，这种经过M-1次奇偶抽选后的排序为序列的倒序。

因此，在运算之前应先对序列x(n)进行倒序。

倒序的规律就是把顺序数的二进制位倒置，即可得到倒序值。

倒序数是在M 位二进制数最高位加一，逢2向右进位。

离散傅里叶变换及其快速算法

离散傅里叶变换及其快速算法


ak 也是以 N周期的周期序列，满足 ak
~ X (k ) Nak
ak 。令 ln
（3.5）
将式（3.4）代入，得
N 1 j kn ~ ~ N X ( k ) x ( n )e n 0 2
k
（3.6）
~ X (k ) 式中， 是以N为周期的周期序列，称为
~ x (n) 的离散傅里叶级数，用DFS表示。
~(k )， N 相位为 幅度为 X
~ arg[ X (k )]
。
基波分量的频率为 2 N ，幅度为
~ 为arg[ X (1)]
~ X (1) N
，相位
。
x ( n ) 以 N 8 为周期 n) 【例3-1】设 x(n) R4 (，将
进行周期延拓，得到周期序列 幅频特性。
~ x ( n)
2016-12-8
解：根据定义求解

14 12 e 8e
j
j
2 k 6
10e
j
j
2 2k 6 j 2 5k 6
2 3k 6
6e
2 4k 6
10e
X (0) 60 X (3) 0
X (1) 9 j 3 3 X (4) 3 j 3
X (2) 3 j 3 X (5) 9 j 3 3
x 3(n )
当k取奇数（ k=2m+1 ，m=0，1，…， N/4-1 ）时
N n(2 m 1) X 1(2m 1) x 1(n ) x 1 n 4 W N 2 n 0 N 4 1 N n mn x 1(n ) x 1 n W W N N 4 4 n 0 2
FFT是离散傅立叶变换的快速算法

FFT是离散傅立叶变换的快速算法

FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。

有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。

这就是很多信号分析采用FFT变换的原因。

另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。

现在圈圈就根据实际经验来说说FFT结果的具体物理意义。

一个模拟信号，经过ADC采样之后，就变成了数字信号。

采样定理告诉我们，采样频率要大于信号频率的两倍，这些我就不在此罗嗦了。

采样得到的数字信号，就可以做FFT变换了。

N个采样点，经过FFT之后，就可以得到N个点的FFT结果。

为了方便进行FFT 运算，通常N取2的整数次方。

假设采样频率为Fs，信号频率F，采样点数为N。

那么FFT之后结果就是一个为N点的复数。

每一个点就对应着一个频率点。

这个点的模值，就是该频率值下的幅度特性。

具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。

而第一个点就是直流分量，它的模值就是直流分量的N倍。

而每个点的相位呢，就是在该频率下的信号的相位。

第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。

例如某点n所表示的频率为：Fn=(n-1)*Fs/N。

由上面的公式可以看出，Fn所能分辨到频率为为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。

1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。

FFT是离散傅立叶变换的快速算法

FFT是离散傅立叶变换的快速算法FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。

有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。

这就是很多信号分析采用FFT变换的原因。

另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。

现在圈圈就根据实际经验来说说FFT结果的具体物理意义。

一个模拟信号，经过ADC采样之后，就变成了数字信号。

采样定理告诉我们，采样频率要大于信号频率的两倍，这些我就不在此罗嗦了。

采样得到的数字信号，就可以做FFT变换了。

N个采样点，经过FFT之后，就可以得到N个点的FFT结果。

为了方便进行FFT 运算，通常N取2的整数次方。

假设采样频率为Fs，信号频率F，采样点数为N。

那么FFT 之后结果就是一个为N点的复数。

每一个点就对应着一个频率点。

这个点的模值，就是该频率值下的幅度特性。

具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT 的结果的每个点（除了第一个点直流分量之外）的模值就是A 的N/2倍。

而第一个点就是直流分量，它的模值就是直流分量的N倍。

而每个点的相位呢，就是在该频率下的信号的相位。

第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。

例如某点n所表示的频率为：Fn=(n-1)*Fs/N。

由上面的公式可以看出，Fn所能分辨到频率为为Fs/N。

如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。

1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。

离散傅里叶变换及其快速算法


w nk N
又如
w
N N
/
2
1,
因此
w(kN / 2) N
wNk
利用这些周期性和对称性，使DFT运算中有些项可合并；
2）利用
w
nk N
的周期性和对称性，把长度为N点的大点数的DFT
运算依次分解为若干个小点数的DFT。因为DFT的计算量正比于N2，
N小，计算量也就小。
FFT算法正是基于这样的基本思想发展起来的。它有多种形式，
n0
N / 21
X (2r 1) [x(n) x(n N / 2)]WNn(2r1)
n0
N / 21
[x(n) (n)=x(n)+x(n+N/2) b(n)=[x(n)-x(n+N/2]wnN
这两个序列都是N/2点的序列，将其代入上两式，得
结果仍然储存在同一组存储器中，直到最后 输出，中间无需其它存储器，这叫原位计算 。 每一级运算均可在原位进行，这种原位运算 结构可节省存储单元，降低设备成本，还可 节省寻址的时间。
21
（3）序数重排
对按时间抽取FFT的原位运算结构，当运算完毕
时，正好顺序存放着 X（0），X（1），X（2），
…，X（7），因此可直接按顺序输出，但这种原
但基本上可分为两类：时间抽取法和频率抽取法。
6
2、按时间抽取的FFT（N点DFT运算的分解） 先从一个特殊情况开始，假定N是2的整数次方，
N=2M，M：正整数
首先将序列x（n）分解为两组，一组为偶数项，一组为奇数 项，
x(2r) x1(r) x(2r 1) x2 (r
)
r 0,1,, N/2-1
位运算的输入 x（n）却不能按这种自然顺序存入

快速傅立叶变换(FFT)算法实验

快速傅立叶变换(FFＴ)算法实验实验目得:１、加深对ＤFT 算法原理与基本性质得理解；2、熟悉FFT 得算法原理与FFＴ子程序得算法流程与应用;3、学习用FFT 对连续信号与时域信号进行频谱分析得方法。

程序流程图：傅立叶变换就就是一种将信号从时域到频域得变换形式,就就是声学、语音、电信与信号处理等领域中得一种重要分析工具。

离散傅立叶变换(ＤＦＴ)就就是连续傅立叶变换在离散系统中得表现形式,由于DＦT 得计算量很大,因此在很长时间内其应用受到很大得限制。

快速傅立叶变换（FＦT)就就是离散傅立叶变换得一种高效运算方法。

由于我们在计算DFT 时一次复数乘法需用四次实数乘法与二次实数加法；一次复数加法则需二次实数加法。

运算一个X（k）需要4N 次复数乘法及2N+2(N－１)=2(2N-1)次实数加法。

所以整个DＦＴ运算总共需要４N^2 次实数乘法与N＊2(2N-1)＝2N(2N-１)次实数加法。

如此一来,计算时乘法次数与加法次数都就就是与N^２成正比得，当N 很大时，运算量就就是可观得,因而需要改进对DFT 得算法减少运算速度。

我们可以将DＦT 运算中有些项合并。

我们先设序列长度为N＝2＾L，L为整数。

将N=2^L 得序列x(n)(n=0,1,……,N－１）,按N得奇偶分成两组,也就就就是说我们将一个N 点得DFT 分解成两个N/2点得DFT，她们又重新组合成一个如下式所表达得N 点DＦT:一般来说,输入被假定为连续得。

当输入为纯粹得实数得时候,我们就可以利用左右对称得特性更好得计算ＤFT。

这样得ＲFFＴ优化算法就就是包装算法：首先２N 点实数得连续输入称为“进包”。

其次N 点得ＦＦT被连续运行。

最后作为结果产生得N 点得合成输出就就是“打开”成为最初得与DFT 相符合得２N 点输入。

使用这一思想，我们可以划分FFT得大小,它有一半花费在包装输入Ｏ(N)得操作与打开输出上。

AD原理图源程序#include<matｈ、h>#ｉncluｄe"DSP２833x_Device、h"／/ DSＰ2833x Header "DSP2８33x_Ｅxａmｐｌeｓ、h"／/ ＤSＰ2833x Ｅxamｐles Ｉｎｃlｕｄe Ｆi#incｌude＂m、h"＃inｃlude"i_ｃmｐlx、h"#ｉｎcluｄe＂eｘt_ｉnf、h"/*****＊********＊*＊**＊***＊****＊*******＊＊***＊＊**＊**＊*＊****＊*＊**＊******＊*＊*******＊***/#if (CＰU＿FＲQ＿1５0MHZ) // Dｅfaｕlt － 150 MHｚ SYSCLＫＯUT#ｄefineＡDＣ＿ＭODCＬK ０x３// HSPCLK ＝SＹＳCＬKOUT/2*ADC_MODCLK2 ＝ 150／(2＊３) = 25、0 MHz#endiｆ#if (CPU_ＦＲＱ_1０0ＭHZ）#define ADC_MODCＬK 0x２//ＨSPCLK = ＳYSCLKＯUＴ/２*AＤＣ_MOＤCＬK２ = 100／(２*２) = ２5、0 MＨz#eｎdiｆ#defiｎe ADC_ＣKPS 0x1/／ ADC modulｅｃｌoｃｋ =HSPCＬK/2*ＡDC_CKＰS = 2５、0MHz/(1＊２) = 1２、5MHｚ#dｅfineＡＤC_SＨＣLK0xf /／Ｓ/H ｗｉdtｈin ADＣmｏdule periｏds ＝ 1６ AＤC ｃlｏｃｋs#defineＡVG 1000 // Aｖｅrage sample liｍit#deｆine ZOＦＦSET ０ｘ00 ／/ Average Zerｏ offｓet#defiｎｅ BＵF_SIZＥ16０// Samｐｌｅ buｆfer siｚe/*********＊****＊*****＊****＊*＊********＊＊***＊＊＊***＊＊*＊＊＊******＊＊******＊*************/／/////／/////／／///ｕnｓigneｄiｎｔＳamｐｌeLong;＃ｄefｉne SAMPＬELONG 3//////////／//／/／／///unｓignｅd inｔ Aｄ_datａ[１536]={0｝；unｓigｎeｄiｎt Aｄ_ｄata１[１５36]={0}；uｎsigned int coｎvcｏunt ＝ 0；volatile unsiｇned intａdcoｎvoveｒ =0;///／/////////／／/iｎt m＝0;dｏuｂle n;douｂlｅ p,q;PLEX DDataBufｆｅｒ［51２]={０};Uｉnt3２ moｄ[512］;／/////／／/////／////／／//unsiｇｎedｉnt i；／*＊**＊*************＊****＊*＊*****＊***＊＊**＊**＊**＊*＊**＊＊＊*******＊＊***＊＊*＊****＊＊*＊＊＊＊＊/// Protoｔypｅ statementｓ fｏｒ fｕｎcｔionｓｆoｕnd within this file、iｎteｒrｕptｖoｉｄadc_isr(voiｄ)；/**＊＊**＊***********＊***＊***＊**********＊＊＊＊＊******＊*＊＊*＊*＊＊*＊*****＊***＊**********＊*/void maｉn(void){ﻩ#if SＡＭPLＥLONG==1ﻩSａｍｐleLonｇ =２56;#endif＃ｉf SAMＰLＥLOＮG=＝2ﻩSaｍpleLong=5１2;ﻩ#endif#ifＳAMPLEＬＯＮG==3ﻩＳampleLoｎｇ＝１0２４;ﻩ＃enｄif// Sｔeｐ 1、Initialｉze Systｅｍ Coｎtrol：/／ PLL，ＷatｃhＤog, enaｂｌe Ｐeｒｉphｅrａl Clockｓ//Thｉｓ example fｕnctioｎ iｓｆｏｕnd in thｅ DSP2８33x＿SysCtrl、c ｆilｅ、InｉtSｙsCtrl（)；/／ Step 2、 Initialize GPIＯ：／／ Thiｓｅxample fuｎｃtiｏn is fouｎd in ｔhe DSP283３x＿Gｐｉo、c// iｌlusｔrａtｅs hoｗ to seｔｔhe GPIＯｔｏ iｔ＇ｓ dｅfａulｔ sｔaｔｅ、InitGpｉo（); //Skｉｐｐed for thiｓ exaｍplｅ// Sｔep3、Ｃlｅaｒall interruｐｔs and initiaｌize PＩE ｖeｃtor table://Disａble CＰUｉnteｒruptsDＩＮT;//Inｉtialize the PIEｃontｒol regｉｓters tｏthｅir ｄefaulｔｓｔate、// The dｅfauｌtｓtaｔe is aｌl ＰＩE ｉnｔerruｐｔs dｉsabｌed aｎd flag ｓ// ａre cｌeared、／/ This function iｓfoｕｎｄin the DSＰ２833ｘ_PｉｅＣtｒl、c ｆile、ＩnitPieCtｒl()；／/ Diｓablｅ CPU inｔerrupts and ｃleａr all CPＵｉnｔeｒruｐt ｆlａｇs： IER = 0x０000;IＦR = 0ｘ00０0;/／ Initiａｌize the ＰIE vectｏr tａbｌe wiｔｈ pointers tｏ tｈe shell Int ｅｒｒupt/／ Servｉce Ｒoｕtines (ISR）、/／ Thisｗｉｌl poｐulａtｅｔhe entiｒe tabｌe, eｖen if thｅinｔｅｒｒｕpt/／ is not usedｉn tｈiｓ eｘamｐle、 This is ｕｓeful for debｕg pｕrpose ｓ、//Tｈｅ shell ISR routiｎｅｓ are founｄ in DSP28３3x＿ＤefａuｌtＩｓr、ｃ、// Thisｆｕnｃtiｏｎis fｏund iｎＤSP28３3x＿PieVｅcｔ、c、ＩnitＰieＶectＴaｂｌe();／/Ｉｎｔerrupts thaｔare uｓed iｎｔｈiｓexａmｐle arｅ rｅ-mａｐped tｏ// IＳRｆｕnctionｓ found wｉthin thiｓ file、EALLOＷ; ／／Ｔhis is neeｄeｄｔo wrｉte ｔo EALLOW ｐroteｃtｅd regi ｓｔｅrPieＶectTａble、AＤＣIＮT= &aｄc_ｉsr；EＤIS; // This iｓ neｅded ｔｏ disａble write ｔｏ EALＬOW ｐrｏte ｃteｄ rｅgisteｒs／/ Ｓteｐ 4、 Inｉtialize all ｔｈｅＤeｖicｅ Peｒiphｅralｓ:// Tｈiｓ fｕｎctioｎ is fouｎd in DＳP２833x_InitPeripｈerａls、c// InitPｅｒｉpｈerals();// Noｔrequirｅd ｆｏr thｉs exampleIｎitAdc();/／ For this eｘａmｐle, iｎit thｅ ADC// Steｐ５、Ｕser sｐeciｆic coｄe,ｅｎablｅ iｎterrｕptｓ://Ｅｎable ADCINTｉn ＰIEPiｅCｔrｌReｇs、PIEIER1、ｂit、INTｘ6 = １;ＩER|= M_INT1; ／/Eｎable ＣPU Inteｒrupt1EINＴ；／／ Enable Ｇｌｏｂaｌ intｅｒｒupt ＩＮTＭERTM；/／ EnablｅＧloｂａl reａｌtime intｅrrｕpt DＢGＭＡdｃＲｅgs、ADCＴRL1、ｂit、ACQ_ＰS =ＡDC＿SＨＣLＫ；ＡdcRegs、ＡＤCTRL3、ｂｉt、ＡDＣCLＫＰＳ = ADＣ_CKPＳ；ＡdｃRegs、AＤＣTRL1、bｉｔ、ＳＥQ_ＣASC ＝1; // 0 Nｏn-Ｃas ｃａｄed Mｏde; 1 Ｃａｓcadｅd MoｄeAｄcRegs、AＤCTＲL2、ｂit、INT_EＮA_SEQ１ = 0x1；ＡdcRegs、AＤCTＲＬ2、ｂit、RＳT_ＳEQ1= 0x1;AdcRegs、AＤCＣHＳＥLＳEＱ１、ｂit、CONV00 ＝ 0x6;AdcReｇs、ADCMAＸCＯＮV、ｂit、MAX_ＣONV1 = １5;AdcRｅgs、AＤCTRL2、ｂｉt、SOC_SEQ1 =０x1;for（;;)｛ﻩｉf（ａdconvovｅr=＝1){ﻩﻩﻩfoｒ（i＝0;ｉ＜(SaｍpｌeLong/2)；i＋+）ﻩﻩﻩ｛ﻩﻩDDatａBuffｅｒ[i]、real＝Ad＿daｔa[2*ｉ];//sｈort inｔﻩﻩＤDａtaＢuｆｆeｒ[i]、ｉmag=Ad＿dａta［2*ｉ+１]；//ｓhort iｎｔﻩﻩ｝ﻩﻩswitｃh（SamｐleＬong)ﻩﻩﻩ{ﻩﻩｃaｓe256：/*25６point*/ﻩfft２５6(DDａｔaＢuffeｒ,25６)；m=０;ﻩfoｒ（ｉ=0；i<１2８;i++)ﻩﻩ{ﻩﻩp=ＤDａtａBufｆeｒ［i]、reａl;ﻩｑ=DDatａBufｆeｒ[i］、imag；ﻩﻩﻩﻩn=(long)p*（long)p＋（loｎg)ｑ*(ｌｏｎg)ｑ;mod［m]＝sqrt（n)；ﻩm++;ﻩﻩ}ﻩﻩbreak;ｃase 512: /＊５1２ pｏint*／ﻩ ffｔ51２（DＤataBufｆｅr，512);m=0;ﻩｆor（ｉ=0;i<256;i++)ﻩﻩﻩﻩ{ﻩp=ＤＤataBｕffer[ｉ]、real;ﻩq=DDataBｕffｅr[i］、iｍag;ﻩﻩﻩﻩn=(long）p＊(long）ｐ+(long)q*(ｌｏng)ｑ;ﻩﻩmod[m]=sｑrｔ(n)；ﻩﻩｍ++;ﻩﻩﻩﻩ}ﻩﻩbrｅak;ﻩﻩcaｓｅ 1024：/*1024pｏｉnt*/ﻩﻩfft１024（ＤＤａtaBuｆfer,1024）;ﻩm=0;fｏｒ(i=0;i<５1２;ｉ＋+)ﻩ｛ｐ=DDatａBuffer［ｉ］、reaｌ；ﻩﻩq＝DDataＢｕfｆer[ｉ]、ｉｍaｇ;n=（lｏｎg）p*(ｌonｇ）ｐ+(long)q*(lｏnｇ)q；ﻩﻩﻩｍｏd[m］=sqｒt(n）;ﻩﻩm＋+;}ﻩbrｅak;｝ﻩａdconvoｖeｒ=0;ﻩ cｏnvcounｔ＝0;ﻩﻩﻩﻩ}ﻩ}}intｅrｒuｐt vｏid aｄc_isｒ（void）{/／Iｆ40 cｏnveｒｓioｎｓ haｖe been logged, starｔ overif（cｏnｖcouｎt == ＳａmpleＬong){ａdcoｎvover ＝ 1；｝else｛Ad_data[conｖｃｏunt]= AdcRegs、ＡDCＲESULT0 >>４;coｎｖcouｎｔ++；}／/ Reｉｎiｔialize ｆorｎexｔ ADＣ sequeｎceAdcＲｅgｓ、ADCTRL2、bｉt、RＳT_SEQ1 = 1; //Resｅt SEQ１AdcRegs、ＡDCSＴ、ｂit、INＴ＿SEQ1＿CLR ＝1；／/Clｅar INＴ SEQ1 bitPｉｅCtrlＲｅgs、PIEAＣK、all = PＩＥACK_GROUP1；// Acｋｎoｗｌedge in ｔerruptｔo PIEAdcReｇs、ADCTRL2、ｂit、SＯC_SＥQ1 = 0x1;return;}。

fft计算公式

快速傅里叶变换（FFT）是一种计算离散傅里叶变换（DFT）及其逆变换的高效算法。

FFT的计算公式如下：
X[k] = ∑(n=0 to N-1) x[n] * W[k*n]
其中，X[k]表示离散傅里叶变换的输出，x[n]表示输入的时域信号，N表示输入信号的采样点数，W[k*n]表示复数单位元，即W[k*n] = e^(-2πikn/N)。

对于逆变换，可以使用以下公式：
x[n] = ∑(k=0 to N-1) X[k] * W[-k*n] / N
其中，x[n]表示输入的时域信号，X[k]表示离散傅里叶变换的输出，N表示输入信号的采样点数，W[-k*n]表示复数单位元的逆变换。

这些公式可以根据实际需求进行适当的修改和扩展，例如对于实数信号可以省略虚部，对于对称性可以优化计算等。

离散傅里叶变换及其快速计算方法(DFT、FFT)


0
2 （弧度，数字频率）
0
fs /2
fs f （Hz，模拟频率）
0
s /2
s （弧度/秒，模拟角频率）
25
DFS 定义：几点说明
频率成份
•
直流分量：
当 k=0 时， 号的直流分量（DC
N 1
X%(0) x%(n)WN 0n n0
Component），
N 1
x%(n)
，n此0是时信X%(得号0)到/的N的平傅均里值叶；级数的系数称为信
1
X%(k
)e
j
(
2 N
)km
N k0
变量m替换为n，得
x%(n)
1 N
N
1
X%(
k
)e
j
(
2
N
) kn
k0
1 N
N 1
X%(k )WN kn
k0
21
DFS 定义：反变换
DFS 变换对：时域周期序列与频域周期序列间的关系
N 1
X%(k ) x%(n)WN kn
n0
x%(n)
1 N
N 1
5
3.1 问题的提出：傅里叶变换的四种形式 （2）
1. 连续信号（非周期）的付氏变换
x(t)
X ()
t
x(t) X (),
t
x(t) 1 X ()e jt d
2
X () x(t)e jt dt
时域连续函数造成频域是非周期的谱 时域的非周期造成频域是连续的谱
6
3.1 问题的提出：傅里叶变换的四种形式 （3）
（1）必须是时间限x制(n（) 有 限 时宽0）,
其它
0

离散傅里叶变换及快速算法


序列分解为N个谐波相关的复指数之和。将
j 2N nk
X (k ) x(n)e
, k 0,1,2,
（5-3）
称之为离散傅里叶级数DFS的k次谐波系数。是一个基波周 期为N的周期序列。
X (k ) X ( k N )
§5．离散傅里叶变换及快速算法
在DFS变换中引入复数
k
X ( jk0 )e jk0t
*时域周期为Tp, 频域谱线间隔为2π/Tp
时域信号 连续的 周期的
频域信号
非周期的
离散的
3.离散时间、连续频率的傅立叶变换 – DTFT（离散时间傅立叶 变换） X e 或 X (e ) x(nT) T
j jT
---T 0 T 2T
正 : X (e
WN e
j 2N
将DFS正反变换描述为
nk 正 : X (k ) DFSx (n) X (k ) x (n)WN n 0
N 1
1 N 1 反 : x (n) IDFS X (k ) x (n) X (k )WN nk N k 0


（5-5）
WN
的性质: 1 N 1 ( nm) k 1 n m lN 正交性: WN 0 n m lN N k 0
周期性:
W
k mN N
W
k N
l , m, N / 2, k / 2均为整数
共轭对称性（偶序列）: 可约性：
k N (WN )* WN k
k mk k 2 WN WmN WN // 2
§5．离散傅里叶变换及快速算法
2.离散傅里叶变换（DFT）
但对于数字系统，无论是Z 变换还是序列傅立叶变换的适用方面都存 在一些问题，重要是因为频率变量的连续性性质（DTFT变换出连续频 谱），不便于数字运算和储存。 参考DFS，可以采用类似DFS的分析方法解决以上问题。可以把有限 长非周期序列假设为一无限长周期序列的一个主值周期，即对有限长非 周期序列进行周期延拓，延拓后的序列完全可以采用DFS进行处理，即 采用复指数基频序列和此有限长时间序列取相关，得出每个主值在各频 率上的频谱分量以表示出这个“主值周期”的频谱信息。 由于DFT借用了DFS，这样就假设了序列的周期无限性，但在处理时 又对区间作出限定（主值区间），以符合有限长的特点，这就使DFT带 有了周期性。另外，DFT只是对一周期内的有限个离散频率的表示，所 以它在频率上是离散的，就相当于DTFT变换成连续频谱后再对其采样， 此时采样频率等于序列延拓后的 周期N，即主值序列的个数。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

int n, mmax, m, j, istep, i; double wtemp, wr, wpr, wpi, wi, theta; double tempr, tempi; n = nn << 1; j = 1; for (i = 1; i < n; i += 2) { if (j > i) { tempr = data[j]; data[j] = data[i]; data[i] = tempr; tempr = data[j+1]; data[j+1] = data[i+1]; data[i+1] = tempr; } m = n >> 1; while (m >= 2 && j > m) { j -= m; m >>= 1; } j += m; } mmax = 2; while (n > mmax) { istep = 2*mmax; theta = TWOPI/(isign*mmax); wtemp = sin*theta); wpr = *wtemp*wtemp; wpi = sin(theta); wr = ; wi = ; for (m = 1; m < mmax; m += 2) { for (i = m; i <= n; i += istep) { j =i + mmax; tempr = wr*data[j] - wi*data[j+1]; tempi = wr*data[j+1] + wi*data[j];
相关文档：
• • • • • • • • • •
更多相关文档请访问：
} // 将时域点写入 X1 memcpy(X1, TD, sizeof(complex) * count); // 采用蝶形算法进行快速 Fourier 变换 for(k = 0; k < r; k++) { for(j = 0; j < 1 << k; j++) { bfsize = 1 << (r-k); for(i = 0; i < bfsize / 2; i++) { p = j * bfsize; X2[i + p] = X1[i + p] + X1[i + p + bfsize / 2] * W[i * (1<
FFT(离散傅氏变换的快速算法)
FFT(离散傅氏变换的快速算法) 目录 1 算法简介 2DFT 算法 3 源码表示 4MATLAB 中 FFT 的使用方法 1 算法简介编辑 FFT(Fast Fourier Transformation),即为快速傅氏变换,是离散傅氏变换的快 速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法 进行改进获得的。它对傅氏变换的理论并没有新的 FFT 算法图(Bufferfly 算法) 发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是 进了一大步。 设 x(n)为 N 项的复数序列,由 DFT 变换,任一 X(m)的计算都需要 N 次复数乘 法和 N-1 次复数加法,而一次复数乘法等于四次实数乘法和两次实数加法,一次复数 加法等于两次实数加法,即使把一次复数乘法和一次复数加法定义成一次“运 算”(四次实数乘法和四次实数加法),那么求出 N 项复数序列的 X (m),即 N 点 DFT 变换大约就需要 N^2 次运算。当 N=1024 点甚至更多的时候,需要 N2=1048576 次运算,在 FFT 中,利用 WN 的周期性和对称性,把一个 N 项序列(设 N=2k,k 为正整 数),分为两个 N/2 项的子序列,每个 N/2 点 DFT 变换需要(N/2)2 次运算,再用 N 次 运算把两个 N/2 点的 DFT 变换组合成一个 N 点的 DFT 变换。这样变换以后,总的 运算次数就变成 N+2*(N/2)^2=N+(N^2)/2。继续上面的例子, N=1024 时,总的 运算次数就变成了 525312 次,节省了大约 50%的运算量。而如果我们将这种“一 分为二” 的思想不断进行下去,直到分成两两一组的 DFT 运算单元,那么 N 点的 DFT 变 换就只需要 Nlog2N 次的运算,N 在 1024 点时,运算量仅有 10240 次,是先前的直 接算法的 1%,点数越多,运算量的节约就越大,这就是 FFT 的优越性。 2DFT 算法编辑 For length N input vector x, the DFT is a length N vector X, with elements
data[j] = data[i] - tempr; data[j+1] = data[i+1] - tempi; data[i] += tempr; data[i+1] += tempi; } wr = (wtemp = wr)*wpr - wi*wpi + wr; wi = wi*wpr + wtemp*wpi + wi; } mmax = istep; } } 在 C++环境下的源码 bool FFT(complex * TD, complex * FD, int r) { //一维快速 Fourier 变换。 //complex * TD ——指向时域数组的指针; complex * FD ——指向频域数 组的指针; r ——2 的幂数,即迭代次数 LONG count; // Fourier 变换点数 int i,j,k; // 循环变量 int bfsize,p; // 中间变量 double angle; // 角度 complex *W,*X1,*X2,*X; count = 1 << r; // 计算 Fourier 变换点数为 1 左移 r 位 W = new complex[count / 2]; X1 = new complex[count]; X2 = new complex[count]; // 分配运算所需存储器 // 计算加权系数(旋转因子 w 的 i 次幂表) for(i = 0; i < count / 2; i++) { angle = -i * PI * 2 / count; W[ i ] = complex (cos(angle), sin(angle));
N X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N. n=1 The inverse DFT (computed by IFFT) is given by N x(n) = (1/N) sum X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N. k=1 3 源码表示编辑 在 C 环境下的源码 源码(1): 注:亲测,这个版本无法运行,作者删改了重要内容[1]请参考源码(2) (see pages 507-508 of Numerical Recipes in C) Inputs: data[] : array of complex* data points of size 2*NFFT+1. data[0] is unused, * the n'th complex number x(n), for 0 <= n <= length(x)-1, is stored as: data[2*n+1] = real(x(n)) data[2*n+2] = imag(x(n)) if length(Nx) < NFFT, the remainder of the array must be padded with zeros nn : FFT order NFFT. Thisห้องสมุดไป่ตู้MUST be a power of 2 and >= length(x). isign: if set to 1, computes the forward FFT if set to -1, computes Inverse FFT - in this case the output values have to be manually normalized by multiplying with 1/NFFT. Outputs: data[] : The FFT or IFFT results are stored in data, overwriting the input. */ void four1(double data[], int nn, int isign) {