下载文档原格式
离散傅里叶变换及其快速算法离散傅里叶变换（Discrete Fourier Transform，DFT）是一种将离散信号转换为频域表示的数学工具。
它在信号处理、图像处理、通信等领域有广泛的应用。
而快速傅里叶变换（Fast Fourier Transform，FFT）是一种能够高效计算DFT的算法，大大减少了计算量。
首先，我们来看一下DFT的原理。
给定一个有限长度的离散信号序列x(n)，DFT将其转换为频谱X(k)，其中k为频率索引，取值范围为0到N-1，N为序列的长度。
DFT的定义公式如下：X(k) = Σ x(n) * exp(-j * 2π * nk / N)其中，exp为自然指数函数，j为虚数单位。
DFT将信号分解为了N个复数的和，这些复数代表了不同频率分量在信号中的贡献。
然而，直接计算DFT的时间复杂度非常高，为O(N^2)。
为了提高计算效率，Cooley和Tukey于1965年提出了FFT算法。
FFT算法基于以下性质：若N为2的整数次幂，则DFT可以被分解为两个较小长度的DFT的线性组合。
具体来说，将N个点的DFT拆分为长度为N/2的两个DFT，然后再对这两个子序列进行DFT，最后将两个子序列的结果组合起来。
这个过程可以递归地进行，直到序列长度为1，即可得到最终的DFT结果。
FFT算法的时间复杂度为O(NlogN)，远远小于直接计算DFT的复杂度。
这使得FFT成为了处理大规模数据的首选方法之一、此外，FFT还有其他一些优点，如可并行化计算、对称性质等。
FFT算法可以采用不同的实现方式，最著名的是基于蝶形运算的Cooley-Tukey算法。
这种实现方式将FFT过程分为了两个阶段：置换阶段和蝶形运算阶段。
置换阶段通过将信号重新排序，将原始序列分为奇偶两个子序列，并计算每个子序列的DFT。
这个过程可以递归地应用于子序列，直到长度为1蝶形运算阶段是FFT算法的核心部分。
蝶形运算是指将两个频域上的复数进行运算，得到新的复数。
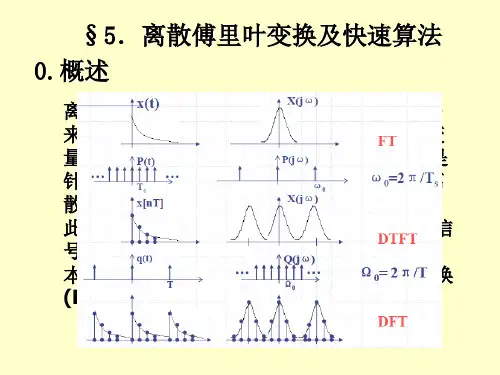
第五章 离散傅里叶变换及其快速算法 1 离散傅里叶变换(DFT)的推导(1) 时域抽样：目的：解决信号的离散化问题。
效果：连续信号离散化使得信号的频谱被周期延拓。
(2) 时域截断：原因：工程上无法处理时间无限信号。
方法：通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果：时域乘以矩形脉冲信号，频域相当于和抽样函数卷积。
(3) 时域周期延拓：目的：要使频率离散，就要使时域变成周期信号。
方法：周期延拓中的搬移通过与)(s nT t -δ的卷积来实现。
表示：延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果：周期延拓后的周期函数具有离散谱。
(4)1。
图1 DFT 推导过程示意图(5) 处理后信号的连续时间傅里叶变换：∑∑∞-∞=-=π--δ⋅⎥⎥⎦⎤⎢⎢⎣⎡=k N n N kn j s kf f e nT h f H )()()(~010/2(i))(~f H 是离散函数，仅在离散频率点SNT k T k kf f ===00处存在冲激，强度为k a ，其余各点为0。
(ii) )(~f H 是周期函数，周期为ss T NT N T N Nf 100===，每个周期内有N 个不同的幅值。
(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT 及IDFT 的定义(1) DFT 定义：设()s nT h 是连续函数)(t h 的N 个抽样值1,,1,0-=N n ，这N 个点的宽度为N 的DFT 为：[])1,...,1,0(,)()(10/2-=⎪⎪⎭⎫⎝⎛==∆-=π-∑N k NTk H enT h nT h DFT s N n Nnk j s s N (2) IDFT 定义：设⎪⎪⎭⎫⎝⎛s NT kH 是连续频率函数)(f H 的N 个抽样值1,,1,0-=N k ， 这N 个点的宽度为N 的IDFT 为：())1,...,1,0(,110/21-==⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛∆-=π--∑N k nT h e NTkH NNT kH DFT s N k N nk j s sN (3) N nk j e /2π-称为N 点DFT 的变换核函数，N nk j e /2π称为N 点IDFT 的变换核函数。
它们互为共轭。
(4) 同样的信号，宽度不同的DFT 会有不同的结果。
DFT 正逆变换的对应关系是唯一的，或者说它们是互逆的。
(5) 引入N j N e W /2π-=(i) 用途：(a) 正逆变换的核函数分别可以表示为nk N W 和nkN W -。
(b) 核函数的正交性可以表示为：())(*10r n N W W krN N k kn N-δ=∑-= (c) DFT 可以表示为：)1,,1,0(,)(10-==⎪⎪⎭⎫ ⎝⎛∑-=N k W nT h NTkH N n nk N s s(d) IDFT 可以表示为：)1,,1,0(,1)(10-=⎪⎪⎭⎫ ⎝⎛=∑-=-N n W NTk H NnT h N k nk N s s(ii) 性质：周期性和对称性：(a) 12==π-j NNe W (b) 12/-==π-j N Ne W (c) r N r N N N r N N W W W W ==+(d) r N r N N N r N N W W W W -=-=+2/2/(e) )(1Z m W mN ∈∀=(f) ),(/2/2Z n m W e eW nN N n j m N m n j m n m N ∈∀===π-π- 3 离散谱的性质(1) 离散谱定义：称)(Z k NT k H H S k ∈⎪⎪⎭⎫⎝⎛=∆为离散序列)0)((N n nTs h <≤的DFT 离散谱，简称离散谱。
(2) 性质：(i) 周期性：序列的N 点的DFT 离散谱是周期为N 的序列。
(ii) 共扼对称性：如果)0)((N n nTs x <≤为实序列，则其N 点的DFT 关于原点和N /2都具有共轭对称性。
即*k k H H =-；*k k N H H =-；*22kNkNH H =±(iii) 幅度对称性：如果)0)((N n nTs x <≤为实序列，则其N 点的DFT 关于原点和N /2都具有幅度对称性。
即k k H H -=；k k N H H =-；kNkNH H 22=±(3) 改写： (i) 简记)(s nT h 为)(n h(ii) 简记⎪⎪⎭⎫⎝⎛s NT k H 为)(k H (iii) DFT 对简记为：)()(k H n h D FT⇔或)()(k H n h ⇔(iv) ()[])1,,1,0(,)()(1-===∑-=∆N k W n h n h DFT k H N n nkN(v)[]())1,,1,0(,1)()(101-===∑-=--∆N n W k H Nk H DFT n h N k nkN4 DFT 总结(1) DFT 的定义是针对任意的离散序列)(nTs x 中的有限个离散抽样)0(N n <≤的，它并不要求该序列具有周期性。
(2) 由DFT 求出的离散谱)()(Z k NT k H H k H S k ∈⎪⎪⎭⎫⎝⎛==∆是离散的周期函数，周期为s s s f T NT N T N Nf ====1/00、离散间隔为0011f T N f NT s s ===。
离散谱关于变元k 的周期为N 。
(3) 如果称离散谱经过IDFT 所得到的序列为重建信号，))(('Z n nTs x ∈，则重建信号是离散的周期函数，周期为001f T NT s ==(对应离散谱的离散间隔的倒数)、离散间隔为001/Nf N T N NT T s s ===(对应离散谱周期的倒数)。
(4) 经IDFT 重建信号的基频就是频域的离散间隔，或时域周期的倒数，为SNT T f 1100==。
(5) 实序列的离散谱关于原点和2N(如果N 是偶数)是共轭对称和幅度对称的。
因此，真正有用的频谱信息可以从0~12-N范围获得，从低频到高频。
(6) 在时域和频域N ~0范围内的N 点分别是各自的主值区间或主值周期。
5 DFT 性质(1) 线性性：对任意常数m a (M m ≤≤1)，有[]∑∑==⇔⎥⎥⎦⎤⎢⎢⎣⎡M m m m M m m m n x DFT a n x a DFT 11)()((2) 奇偶虚实性：(i) DFT 的反褶、平移：先把有限长序列周期延拓，再作相应反褶或平移，最后取主值区间的序列作为最终结果。
(ii) DFT 有如下的奇偶虚实特性：奇⇔奇；偶⇔偶；实偶⇔实偶；实奇⇔虚奇；实 ⇔(实偶) + j(实奇)；实 ⇔(实偶)·EXP(实奇)。
(3) 反褶和共轭性：(4) 对偶性：)()(k Nx n X -⇔(i) 把离散谱序列当成时域序列进行DFT ，结果是原时域序列反褶的N 倍； (ii) 如果原序列具有偶对称性，则DFT 结果是原时域序列的N 倍。
(5) 时移性：kmN W k X m n x )()(⇔-。
序列的时移不影响DFT 离散谱的幅度。
(6) 频移性：)()(l k X W n x nl N -⇔-(7) 时域离散圆卷积定理：)()()()(k Y k X n y n x ⇔⊗(i) 圆卷积：周期均为N 的序列)(n x 与)(n y 之间的圆卷积为∑-=-=⊗1)()()()(N i i n y i x n y n x)()(n y n x ⊗仍是n 的序列，周期为N 。
(ii) 非周期序列之间只可能存在线卷积，不存在圆卷积；周期序列之间存在圆卷积，但不存在线卷积。
(8) 频域离散圆卷积定理：)()(1)()(k Y k X Nn y n x ⊗⇔(9) 时域离散圆相关定理：)()()(*)(k Y k X n R P xy⇔ 周期为N 的序列)(n x 和)(n y 的圆相关：()∑-=∆-==10*)()()()()()(),(N i P xy P n i y i x n R n y n x R是n 的序列，周期为N 。
(10) []{}**)(1)(k H DFT Nn h k =。
其中[]⋅kDFT 表示按k 进行DFT 运算。
(11) 帕斯瓦尔定理： ∑∑-=-==102102)(1)(N k N n k X Nn x6 快速傅里叶变换FFT(1) FFT 不是一种新的变换，而是DFT 的快速算法。
(2) 直接DFT 计算的复杂度：)(2N O计算DFT 需要：2*N N N =次复数乘法；2*N N N =次复数加法。
(3) FFT 算法推导：(i) 第L 次迭代中对偶结点值的计算公式为：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧->>===-⎪⎩⎪⎨⎧-=+=-----))((22)()()()()()(1111L r K BR P N K K W K x K x K x W K x K x K x L r LL L r L L P N L L L L LL P N L L L L L L LL，L K 是循环控制变量。
(ii) 对偶结点的关系如图2所示：图2 FFT 中对偶结点关系图 (iii) 旋转因子：kN W 被称为旋转因子，可预先算好并保存。
(iv) 整序：经过r 次迭代后，得到结果()()b r r k k k x 110- ，实际结果应是()()b r k k k X 011 -，所以流程的最后一步是按下标的正常二进制顺序对结果进行整序。
(4) FFT 算法特点：(rN 2=) (i) 共需r 次迭代；(ii) 第)1(r L L ≤≤次迭代对偶结点的偶距为L L r L L N K K 2/2==--，因此一组结点覆盖的序号个数是12)(2-=-L L L N K K 。
(iii) 第)1(r L L ≤≤次迭代结点的组数为[]12)(2/-=-L L L K K N 。
(iv) LP N W 可以预先计算好，而且L P 的变化范围是12~0-N。
(5) FFT 算法流程：(r N 2=)(i) 初始化：10),()(0-≤≤←N n n x n x ； (ii) 第)1(r L L ≤≤次迭代：(a) 下标控制变量初始化0=L K ； (b) “结点对”的个数初始化0=num ;(c) DO Nnum WHILE L)2(<按对偶结点对的计算公式进行置位运算，得到)(L L K x 和)(L L K x 的值； 1+←L L K K ；1+←num num ；跳过已经计算过的结点(即上面L K 所对应的那些结点)：L L N K 2/=+； 如果N K L <，转到b)继续计算下一组结点；否则结束本次迭代。
