下载文档原格式
C60高强混凝土配合比的优化设计摘要：文章以广州黄埔区凤尾村复建住宅工程为背景，对C60高强混凝土的配合比进行详细研究。
通过科学的原材料选择和配合比设计，确保了混凝土性能的优越表现。
通过我们的实验验证，得到的混凝土不仅在和易性上表现优越，而且在抗压强度等力学性能方面具备出色的表现。
最后针对C60微膨胀混凝土的养护要求，提出了详尽的措施，以确保混凝土充分发挥其膨胀效应，提高其耐久性和抗压强度。
通过本文的研究，对于类似工程的混凝土设计与施工提供了有益的经验和指导。
关键词：C60高强混凝土；配合比设计；实验设计1引言C60高强混凝土，作为混凝土等级的一种，具有卓越的抗压强度、耐久性和工作性能。
其在大跨度桥梁、高层建筑和其他重要工程中的广泛应用，对于提升我国基础设施的整体质量具有积极的意义[1]。
混凝土的性能直接受配合比的影响，而C60高强混凝土的配合比设计则成为提高工程质量和性能的关键环节。
通过精心设计和优化混凝土的组成部分，可以实现对混凝土强度、耐久性和施工性能的综合优化。
广州黄埔区凤尾村复建住宅（ZSCB-C1-1地块）总承包工程作为其中的代表项目，由于施工工艺和混凝土性能的复杂性，对C60高强混凝土的配合比设计提出了更高的要求。
因此，本论文旨在通过深入研究C60高强混凝土的配合比设计，探讨不同原材料及掺合料的选择、水胶比的优化以及添加剂的应用，以实现C60高强混凝土的性能最大化。
2工程概况广州黄埔区凤尾村复建住宅（ZSCB-C1-1地块）总承包工程位于广州市黄埔区中，项目供应混凝土总计70000m³，且C60高强混凝土方量较多，采用现浇混凝土施工工艺。
而与传统预拌混凝土相比，现浇混凝土对坍落度的控制和易性的要求更为严格，对施工流程的合理安排也提出了更高的挑战。
同时也需要我们设计优化C60高强混凝土的配合比来确保凝土到场和易性，控制好混凝土坍落度的损失。
3混凝土技术要求和原材料选择3.1技术要求为保证新拌混凝土具有较好的工作性能，防止产生泌水、分层、离析等问题，提出新拌混凝土坍落度要求为180±20mm且60min内坍落度不大于30mm。
最优化方法-习题解答张彦斌计算机学院2014年10月20日Contents1第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、412第二章线搜索算法-P27习题2、4、643第三章最速下降法和牛顿法P41习题1，2，374第四章共轭梯度法P51习题1，3，6(1)105第五章拟牛顿法P73-2126第六章信赖域方法P86-8147第七章非线性最小二乘问题P98-1，2，6188第八章最优性条件P112-1，2,5,6239第九章罚函数法P132，1-(1)、2-(1)、3-(3),62610第十一章二次规划习题11P178-1（1），5291第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、4 1.验证下列各集合是凸集:(1)S={(x1,x2)|2x1+x2≥1,x1−2x2≥1};需要验证：根据凸集的定义，对任意的x(x1,x2),y(y1,y2)∈S及任意的实数λ∈[0,1],都有λx+(1−λ)y∈S.即,(λx1+(1−λ)y1,λx2+(1−λ)y2)∈S证：由x(x1,x2),y(y1,y2)∈S得到，{2x1+x2≥1,x1−2x2≥12y1+y2≥1,y1−2y2≥1(1)1把(1)中的两个式子对应的左右两部分分别乘以λ和1−λ,然后再相加，即得λ(2x1+x2)+(1−λ)(2y1+y2)≥1,λ(x1−2x2)+(1−λ)(y1−2y2)≥1(2)合并同类项，2(λx1+(1−λ)y1)+(λx2+(1−λ)y2)≥1,(λx1+(1−λ)y1)−2(λx2+(1−λ)y2)≥1(3)证毕.2.判断下列函数为凸（凹）函数或严格凸（凹）函数：(3)f(x)=x21−2x1x2+x22+2x1+3x2首先二阶导数连续可微，根据定理1.5，f在凸集上是（I）凸函数的充分必要条件是∇2f(x)对一切x为半正定；（II）严格凸函数的充分条件是∇2f(x)对一切x为正定。
《食品试验优化设计》习题集第一章绪论一、简答题1、什么是试验设计与统计分析？它在食品科学研究中有何作用？2、统计分析的两个特点是什么？3、食品试验设计与统计分析的主要内容、知识框架结构。
第二章统计资料的整理与分析一、名词解释总体个体样本样本容量随机样本参数统计量随机误差系统误差准确性精确性数量性状资料质量性状资料半定量（等级）资料计数资料计量资料全距（极差）组中值次数分布表次数分布图算术平均数无偏估计几何平均数中位数众数调和平均数标准差方差离均差的平方和（平方和）变异系数二、简答题1、如何提高试验的准确性与精确性？2、如何控制、降低随机误差，避免系统误差？3、资料可以分为哪几类？它们有何区别与联系？4、为什么要对资料进行整理？对于计量资料，整理的基本步骤怎样？5、在对计量资料进行整理时，为什么第一组的组中值以接近或等于资料中的最小值为好？6、统计表与统计图有何用途？常用统计图有哪些？常用统计表有哪些？列统计表、绘统计图时，应注意什么？7、统计中常用的平均数有几种？各在什么情况下应用？8、算术平均数有哪些基本性质？9、标准差有哪些特性？10、为什么变异系数要与平均数、标准差配合使用？三、计算对食品科学专业2004级1班10位同学的体重进行测定，测定结果见表1。
试求其平均数、方差、变异系数、标准差、极差、最大值、最小值等。
表1 10位学生的体重测定结果第三章 理论分布与抽样分布一、名词解释必然现象 随机现象 随机试验 随机事件 概率的统计定义 小概率原理 概率分布 随机变量 离散型随机变量 连续型随机变量 概率分布密度函数 正态分布 标准正态分布 标准正态变量（标准正态离差） 双侧概率（两尾概率） 单侧概率（一尾概率） 贝努利试验 二项分布 波松分布 返置抽样 不返置抽样 标准误 样本平均数的抽样总体 中心极限定理 t 分布 二、简答题1、事件的概率具有那些基本性质？2、离散型随机变量概率分布与连续型随机变量概率分布有何区别？3、正态分布的密度曲线有何特点?4、标准误与标准差有何联系与区别?5、样本平均数抽样总体与原始总体的两个参数间有何联系？6、t 分布与标准正态分布有何区别与联系？ 三、计算题1、已知随机变量u 服从N(0，1)，求P(u ＜-1.4)， P(u ≥1.49)， P （｜u ｜≥2.58）， P(-1.21≤u ＜0.45)，并作图示意。
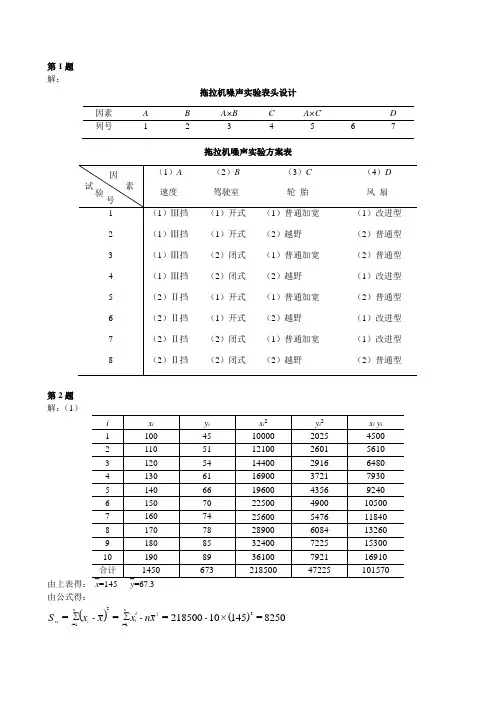
第1题 解：拖拉机噪声实验表头设计因素 A B A×B C A×C D 列号1234567拖拉机噪声实验方案表第2题 解：（1）由上表得：⎺x =145 ⎺y =67.3 由公式得：()()8250=145×10218500=∑=∑=21=21=-x n -x x -x S2ni 2in i ixx()()3985=3.67×145×10101570=•∑=∑=1=1=-y x n -y x y -y x -x S ini iini ixy()()1.1932=3.67×1047225=∑=∑=21=21=-y n -y y -y S 2ni 2ini iyy()47.7=8250×483.01.1932=ˆ=22-S b-SQ xxyye934.0=847.7==ˆ22-n Q σe 735.2=483.0×1453.67=ˆ=ˆ483.0=82503985==ˆ--b x -y aSS bxxxy所以Y 关于x 的一元线性回归方程为：Y=-2.735+0.483x（2）检验假设H 0：b =0，H 1：b ≠0 由（1）中已知的结果及公式xxS σb T ˆˆ=求得：394.45=8250934.0483.0=T又025.0=2α，n -2=8，查出t 0.025(8)=2.306<|T |= 45.394从而|T|在H 0的拒绝域内，故拒绝H 0。
说明回归效果是很显著。
（3）在x 0=145处的预报值为：0y ˆ=Y= 67.2956 t 0.025(8) = 2. 306，⎺x = 145，x 0 -⎺x =0，σˆ=0.9664 又由xx2αS)x -(x n σ-n t x δ02+1+1ˆ)2(=)(，())(+ˆ)(ˆx δyx δ-y 0，得： δ(x 0)=δ(145)=2.306×0.9664101+1= 2.3373预报区间为：(67.2956-2.3373, 67.2956+2.3373)=(64.9583, 69.6329)xy /%散点图xy /%回归线图第3题解：选用正交表L 8(27)()()146=∑908∑90=281=281=i ii i-y --y S 8=8×81=8122jA Δ= S18=12×812= S B5.60=22×812= S C5.4=6×812= S B50=20×812×= S BA误差平方和：S E =S -(S 因+S 交)=146-(8+18+60.5+4.5+50)=5 计算自由度：f =8-1=7 f A = f B = f C = f D =2-1=1 f A × f B =1f E = f –(f 因+f 交)=7-5=2计算均方值：由于各因素和交互作用A ×B 的自由度都是1，因此它们的均方值与它们各自的平方和相等。
