试验优化设计与统计分析作业

5. 泊松分布，≥30 时，用正态分布代替。 51. 抽样分布：统计量的分布概率。
52. 抽样误差：由随机抽样造成的误差。
53. 标准误差（标准误，均数标准误）：样本平均数抽样总体的标准差。反应精确性的高低,x 越大精确度越低。
x
x
n
54. t 分布：在计算 Sx 时,由于采用 S 来代替，使得 t 变量不再服从标准正态分布，而是服从 t 分布。
2) 单个样本平均数的 t 检验：
t 检验：在假设检验中利用 t 分布来进行统计量的概率计算的检验方法。
两个样本平均数的假设检验：由两个样本平均数之差，去判断这两个样本所在的总体平均数有无显著差异。
一、成组资料平均数的假设检验：Biblioteka 1) U 检验1、
如果两个样本资料都服从正态分布，且总体方差
2 1
和
2 2
15. 试样中的误差:随机误差和系统误差。
16. 随机误差（抽样误差）：由许多无法控制的内在和外在偶然因素所造成的误差，不可避免和消除，影响试验
的精确性。
17. 系统误差（片面误差）：由于试验对象相差较大，测量的仪器不准、标准试剂未经校正所引起，可以通过改
进方法、正确试验设计来避免、消除，影响试验准确性。
已知。
2、 总体方差未知，但两个样本都是大样本时，平均数差数的分布呈正态分布。
.
.
2) t 检验
1.
如果两个样本资料都服从正态分布，且
2 1
=
2 2
时，不论是大样本还是小样本，都有下式服从具有
自由度 df=n1+n2-2 的 t 分布： t x1 x2 1 2 。 S x1 x2
.
第二章
5. 总体：根据研究目的确定的研究对象的全体。

《试验设计与数据处理》课程思政探索与实践发布时间：2023-03-16T08:22:04.426Z 来源：《中国科技信息》2022年10月第20期作者：冯振, 陈丰君，陈贺贺[导读] 在深化新时代学校思想政治理论改革创新的背景下，冯振, 陈丰君，陈贺贺河南工学院材料科学与工程学院，河南新乡 453003摘要：在深化新时代学校思想政治理论改革创新的背景下，本文针对我校材料类专业的基础必修课程《试验设计与数据处理》，通过分析本课程的课程思政教学现状，从课程思政建设策略、教学方法、考核方式等方面对本课程的课程思政建设进行探索与实践。

关键词：课程思政；试验设计与数据处理；教学实践；教学改革习近平总书记在全国高校思想政治工作会议上明确指出：“高校立身之本在于立德树人”、“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面”[1]。

《试验设计与数据处理》该学科涉及到化学、数学、统计学、计算机等多门学科，内容涵盖方案的优化、理论公式的推导和计算、试验结果的统计与分析以及计算机软件的应用。

内容多、公式多、计算多等特点，决定了该课程本身的繁杂性[2]。

如何把课程思政教育“立德树人”这一理念融入这门课程的教学工作过程中是个难点，本文针对这一问题进行探索、实践和总结分析。

1 试验设计与数据处理课程思政目标试验设计与数据处理虽然归于数理统计的范畴，但它也属于应用技术学科，具有很强的实用性[3]。

实施试验设计与数据处理课程思政的目的在于：一是使学生掌握试验设计与数据分析的基本原理和基本方法；二是使学生掌握试验设计（正交设计、均匀设计、配方设计）及数据分析（误差分析、直观分析、方差分析、回归分析）等内容，并具备熟练运用Excel进行数据分析的能力；三是要求教师在教学过程中注重提升课程思政意识和职业素养，在传授课程知识的同时，充分挖掘该课程中的思政元素，培养学生树立正确的三观，努力做到“全员育人、全程育人、全方位育人”，提升学生的知识、素质和能力。

食品生物统计附试验设计习题集《食品试验优化设计》习题集第一章绪论一、简答题1、什么是试验设计与统计分析？它在食品科学研究中有何作用？2、统计分析的两个特点是什么？3、食品试验设计与统计分析的主要内容、知识框架结构。

第二章统计资料的整理与分析一、名词解释总体个体样本样本容量随机样本参数统计量随机误差系统误差准确性精确性数量性状资料质量性状资料半定量（等级）资料计数资料计量资料全距（极差）组中值次数分布表次数分布图算术平均数无偏估计几何平均数中位数众数调和平均数标准差方差离均差的平方和（平方和）变异系数二、简答题1、如何提高试验的准确性与精确性？2、如何控制、降低随机误差，避免系统误差？3、资料可以分为哪几类？它们有何区别与联系？4、为什么要对资料进行整理？对于计量资料，整理的基本步骤怎样？5、在对计量资料进行整理时，为什么第一组的组中值以接近或等于资料中的最小值为好？6、统计表与统计图有何用途？常用统计图有哪些？常用统计表有哪些？列统计表、绘统计图时，应注意什么？7、统计中常用的平均数有几种？各在什么情况下应用？ 8、算术平均数有哪些基本性质？ 9、标准差有哪些特性？10、为什么变异系数要与平均数、标准差配合使用？三、计算对食品科学专业2021级1班10位同学的体重进行测定，测定结果见表1。

试求其平均数、方差、变异系数、标准差、极差、最大值、最小值等。

表1 10位学生的体重测定结果1编号体重（kg）1 50.02 52.03 53.54 56.05 58.56 60.07 48.08 51.09 50.510 49.0第三章理论分布与抽样分布一、名词解释必然现象随机现象随机试验随机事件概率的统计定义小概率原理概率分布随机变量离散型随机变量连续型随机变量概率分布密度函数正态分布标准正态分布标准正态变量（标准正态离差）双侧概率（两尾概率）单侧概率（一尾概率）贝努利试验二项分布波松分布返置抽样不返置抽样标准误样本平均数的抽样总体中心极限定理 t分布二、简答题1、事件的概率具有那些基本性质？2、离散型随机变量概率分布与连续型随机变量概率分布有何区别？3、正态分布的密度曲线有何特点?4、标准误与标准差有何联系与区别?5、样本平均数抽样总体与原始总体的两个参数间有何联系？6、t分布与标准正态分布有何区别与联系？三、计算题1、已知随机变量u服从N(0，1)，求P(u＜-1.4)，P(u≥1.49)， P（｜u｜≥2.58）， P(-1.21≤u＜0.45)，并作图示意。

28
单纯形（Simplex）
每个顶点可用对应的坐标表示。如三角形 三个顶点可用坐标（x11, x12）、（x21, x22）、 （x31, x32）来表示。 那么，在试验设计中，每个顶点的坐标可以用 来表示各因素的水平取值；该顶点就表示在该 条件下的一次试验。
如：设有两因素，温度 t，水平为10, 20, 30, … 压力 p，水平为 100, 150, 200, …。则单纯形的 顶点可表示为 (10, 100), (10, 150), (20, 100), …
C 1(1.2) 2(1.5) 3(1.3) 2 3 1 3 1 2 28.3 48.3 40.0 20.0 C2
铁水温度/+1350℃ 15 45 35 40 45 30 40 40 60
通过简单的极差分 析可知，影响因素 从主到次依次为 CAB，最佳条件为 A3B2C2
17
正交试验法的步骤
明确试验目的，确定要考核的试验目标
19
没有合适的正交表时，采用拟水平法。
有交互作用的正交试验设计
交互作用是指因素之间互相影响。
例：某试验田农作物的氮肥、磷肥施用效果
N P
P1=0 200 215
P2=2 225 280
N1=0 N2=3
在实际工作中，交互作用经常遇到，但如果确有把握 认定交互作用的影响很小，则可以忽略不计。
来进行优化
水平：因素在试验中的取值
如用原子吸收分光光度法测定 Cu 时，在选择试验
条件时，若设灯电流分别为 1mA、2mA、3mA、 4mA，狭缝宽度分别为0.1mm、0.2mm、0.4mm， 则灯电流因素有四个水平，狭缝宽度因素有三个水 平。
约束条件：某因素所能取的水平值的变化范围

采用合适的统计分析方法，对实 验结果进行可靠性分析，确保实 验结果真实可信。
06 正交实验设计的发展趋势 和展望
计算机在正交实验设计中的应用
计算机软件
随着计算机技术的发展，越来越多的正 交实验设计软件被开发出来，如Minitab 、SPSS等，这些软件能够快速生成正交 表，进行实验设计和数据分析。
总结词
化学实验设计是正交实验设计的重要应用领域之一，主要用 于探索化学反应条件、优化反应过程和提高产品质量。
详细描述
在化学实验设计中，正交实验设计常常被用于确定最佳的化 学反应条件，如温度、压力、浓度等。通过正交实验，研究 人员可以快速筛选出最佳的反应条件组合，提高实验效率和 准确性。
农业实验设计
实验条件的优化
01
02
03
因素水平选择
根据研究目的和实际情况， 选择合适的因素和水平， 确保实验具有代表性和可 行性。
因素重要程度评估
对各因素进行权重评估， 确定主要影响因素和次要 影响因素。
实验方案制定
根据因素和水平选择，制 定合理的实验方案，确保 实验结果的准确性和可靠 性。
实验误差的控制
实验操作规范
正交表
正交表是一种特殊的表格，用于安排 多因素多水平的实验，具有均衡分散 、整齐可比的特点。
正交表的性质
正交表具有正交性、均匀分散性和代 表性等性质，能够保证实验结果的准 确性和可靠性。
正交实验设计的步骤
选择合适的正交表
根据实验因素和水平数量，选 择合适的正交表，确保实验结 果的准确性和可靠性。
实施实验
确保实验操作规范、准确，减少人为误差。
重复实验
进行重复实验，取平均值，以减小随机误差。
对照实验

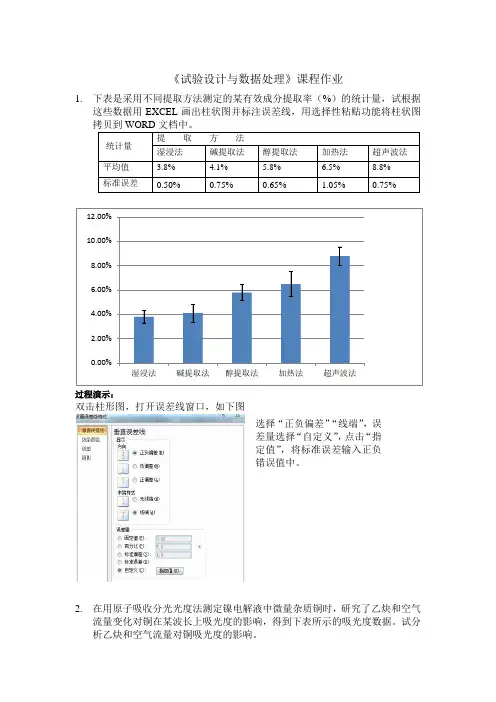
《试验设计与数据处理》课程作业1.下表是采用不同提取方法测定的某有效成分提取率（%）的统计量，试根据这些数据用EXCEL画出柱状图并标注误差线，用选择性粘贴功能将柱状图过程演示：双击柱形图，打开误差线窗口，如下图选择“正负偏差”“线端”，误差量选择“自定义”，点击“指定值”，将标准误差输入正负错误值中。

2.在用原子吸收分光光度法测定镍电解液中微量杂质铜时，研究了乙炔和空气流量变化对铜在某波长上吸光度的影响，得到下表所示的吸光度数据。

试分析乙炔和空气流量对铜吸光度的影响。

实验分析：表中行代表的是乙炔流量，列代表的是空气流量，我们可以看到：F=28.61486>F –crit=3.490295且P-value=9.44E-06<0.01,所以乙炔的流量这个因素对铜的的吸光度的影响非常显著，而在空气流量中F<F-crit且P-value>0.01，所以空气因素对铜吸光度的影响不大。

过程演示：将数据输入Excel表格中，数据分析选择“无重复双因素分析”，具体操作如下图：3.为了研究铝材材质的差异对其在高温水中腐蚀性能的影响，用三种不同的铝材在相同温度的去离子水和自来水中进行了一个月的腐蚀试验，测得的腐蚀程度（μm）如下表所示。

试对铝材材质和水质对腐蚀程度进行方差分析，若显著则分别作多重比较。

方差分析：可重复双因素分析SUMMARY 去离子水自来水总计A1A2A3A4总计实验分析：由方差分析，铝材材质、水源及其交互作用对腐蚀程度均有较大的影响，主次因素从大到小为铝材材质>水源>交互作用。

A已显示同类子集中的组均值。

基于观测到的均值。

a. 使用调和均值样本大小= 6.000。

b. Alpha = .05。

过程演示：4.已知某物质的浓度C与沸点温度T之间关系如下表所示，试绘出散点图，配制出你认为最理想的回归方程式，进行显著性检验并求出该回归方程的标准误差。

SUMMARY OUTPUT：回归统计Multiple R 0.999753R Square 0.999505 Adjusted R Square -1.4标准误差0.089178观测值 1方差分析:df SS MS F回归分析7 80.36881 11.48126 10105.94残差 5 0.039763 0.007953总计12 80.408575.某物质在凝固时放出的热量Y(J/g）与4种化学成分X1、X2、X3、X4有关，试作y与X1、X2、X3、X4的线性回归分析：（1）试求出多元线性回归方程式；（2）对该方程式进行显著性检验，并判定影响热量的化学成分的主次顺序；（3）SUMMARY OUTPUT1234 (2)因P<0.05,故此方程显著。

基于Design-expert的试验设计与统计课程研究生教学改革实践作者：顿国强姜新波来源：《安徽农业科学》2021年第21期摘要为实现农业机械化专业硕士研究生利用课程所学知识解决实际问题能力的培养目标，达到试验设计与统计课程的教学目的，将Design-expert试验设计分析软件引入到试验设计与统计的课程教学中，对教学内容、课程资源、教学模式及考核方式等方面进行了改革实践，提出了翻转课堂+报告+课程论文的教学考核模式。

结果表明，课程改革激发学生学习兴趣，调动学生自主性，降低学习难度，提升了学生使用Design-expert完成试验设计与统计分析应用能力，并锻炼了学生的文献查阅、语言表达、写作技能、科学研究等方面的能力，同时提升了学生的综合素质，显著提高了整体教学质量。

关键词试验设计与统计;design-expert;农业机械化;研究生;教学改革中图分类号 G 642;G 643 文献标识码 A 文章编号 0517-6611（2021）21-0280-03doi：10.3969/j.issn.0517-6611.2021.21.073开放科学（资源服务）标识码（OSID）：The Reform Practice of Test Design and Statistics Courses for Postgraduate Students Based on Design-expertDUN Guo-qiang， JIANG Xin-bo（College of Mechanical and Electrical Engineering，Northeast Forestry University，Harbin，Heilongjiang 150040）Abstract In order to achieve the goal of cultivating the ability of agricultural mechanization postgraduates to solve practical problems by using the knowledge learned in the course， and to achieve the teaching purpose of test design and statistics course， the design-expert test design analysis software was introduced into the teaching of test design and statistics course， reform and practice have been carried out in teaching content， curriculum resources， teaching mode and evaluation mode， the teaching evaluation mode of flipped classroom+report+course paper is put forward，the results show that the curriculum reform stimulates students’ interest in learning，mobilizes students’ autonomy， and reduce the difficulty of learning，it improves the students’ ability of using design-expert to complete the test design and statistical analysis，and exercises students’ literature review， language expression， writing skills and scientific research ability， at the same time， the comprehensive quality of students is improved， and the overall teaching quality is significantly improved.Key words Test design and statistics;Design-expert;Agriculturalmachanization;Postgraduate;Educational reform基金項目东北林业大学教育教学研究项目（DGYYJ2020-2 DGYYJ2021-01）。

试验优化设计与分析(教材)成果总结成果完成人：任露泉，丛茜，杨印生，李建桥，佟金成果完成单位：吉林大学推荐等级建议：二等奖1.立项背景在现代社会实现过程和目标的最优化，已成为解决科学研究、工程设计、生产管理以及其他方面实际问题的一项重要原则。

试验优化技术因其具有设计灵活、计算简便、试验次数少、优化成果多、可靠性高、适用面广等特点，已成为现代设计方法中一个先进的设计方法，成为发达国家企业界人士、工程技术人员、研究人员和管理人员的必备技术，它对于创造利润和提高生产率起着巨大的作用。

因此在我国为了赶超世界先进水平，促进科研、生产和管理事业的发展，编著相关教材，大力推广与应用试验优化技术，不仅具有普遍的实际意义，也具有一定的迫切性。

20世纪80年代初，鉴于国民经济建设实践和科学技术研究中对试验优化技术的广泛需求，为推动教学改革、提高教学质量，任露泉教授对试验优化理论与技术进行了深入系统研究，为本科生开设了“试验设计”课程，为研究生开设了“试验优化技术”课程，并于1987年由机械工业出版社出版了教材《试验优化技术》，产生了很高的学术与技术影响。

2001年任露泉教授在《试验优化技术》一书的基础上编著了《试验优化设计与分析》教材，由吉林科技出版社出版发行。

该教材是对1987年出版的《试验优化技术》的修改、补充和发展。

作者根据对试验优化的教学和科研应用的多年实践与体会，为适应读者学习与使用的实际需要，调整修改了原书中的部分内容和一些方法的设计程式；补充了一些试验优化设计的新方法、新技术；增添了试验优化的一些最新应用实例；并增加了试验优化分析一篇。

本教材2001年获吉林省长白山优秀图书一等奖，2002年被遴选为教育部全国研究生教学用书，再次出版发行，2004年获吉林省教学成果一等奖。

2.教材内容本教材万字，共分三篇二十一章。

第一篇试验设计，除正交设计、干扰控制设计与数据处理等常用技术外,还介绍SN比设计、均匀设计、广义设计、调优运算及稳健设计等正交试验设计技术的拓广应用和现代发展的最新方法；第二篇回归设计，除各种回归的正交设计、旋转设计、饱和设计、多项式设计、还介绍多次变换设计、交互作用搜索设计、混料设计以及D-最优设计等回归设计技术的进一步完善与最新应用技术；在第三篇试验优化技术分析中,介绍了试验数据处理过程中经常遇到的难题及其解决办法，数据分析的最新研究成果及其应用实例。

05
结论
正交试验设计的优势与局限性
高效
通过合理地减少试验次数，提高试验 效率。
全面
能够全面地探索各个因素之间的交互 作用。
正交试验设计的优势与局限性
• 可靠：基于统计理论，结果具有较高的可 靠性。
正交试验设计的优势与局限性
适用范围有限
适用于因素数量和水平数目不太多的情况。
对数据要求较高
需要大量的数据进行分析，且数据质量要高。
促进科学决策
通过正交试验设计和统计分析，能够 为企业或研究机构提供科学依据，促 进科学决策和优化方案制定。
02
正交试验设计的基本原理
正交表的选择与设计
正交表的选择
交互作用和误差控制
根据试验因素的数量、水平数和试验 次数，选择合适的正交表。
考虑因素间的交互作用和误差控制， 确保试验结果的准确性和可靠性。
试验因素和水平的确定
明确试验目的，确定试验因素和水平， 确保试验结果具有实际意义。
Hale Waihona Puke 试验方案的制定试验操作步骤
根据正交表，确定每个试验方案的试验操作步骤。
数据记录
预先设计好数据记录表格，以便准确记录每个试 验方案下的数据。
试验重复
考虑试验的重复性，以提高结果的稳定性和可靠 性。
试验结果的收集
数据整理
方差分析
方差分析的原理
方差分析用于检验各因素对试验指标 的影响是否显著，通过比较各因素的 方差贡献，判断其对试验指标的影响 程度。
方差分析的应用
在正交试验设计中，方差分析可用于 确定显著影响因素，并进一步优化试 验条件。
回归分析
回归分析的原理
回归分析通过建立数学模型描述各因素与试验指标之间的数量关系，并预测不同因素水平下试验指标 的变化趋势。

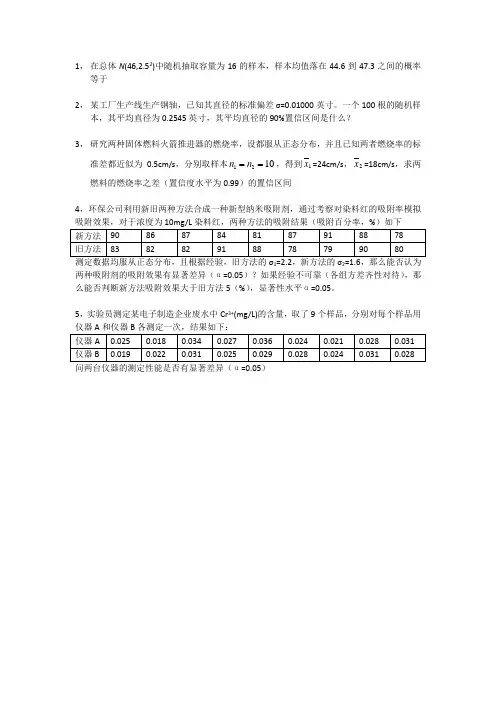
1，在总体N(46,2.52)中随机抽取容量为16的样本，样本均值落在44.6到47.3之间的概率等于
2，某工厂生产线生产钢轴，已知其直径的标准偏差σ=0.01000英寸。

一个100根的随机样本，其平均直径为0.2545英寸，其平均直径的90%置信区间是什么？
3，研究两种固体燃料火箭推进器的燃烧率，设都服从正态分布，并且已知两者燃烧率的标
准差都近似为0.5cm/s，分别取样本
1210
n n
==，得到1x=24cm/s，2x=18cm/s，求两燃料的燃烧率之差（置信度水平为0.99）的置信区间
4，环保公司利用新旧两种方法合成一种新型纳米吸附剂，通过考察对染料红的吸附率模拟吸附效果，对于浓度为10mg/L染料红，两种方法的吸附结果（吸附百分率，%）如下
测定数据均服从正态分布，且根据经验，旧方法的σ1=2.2，新方法的σ2=1.6，那么能否认为两种吸附剂的吸附效果有显著差异（α=0.05）？如果经验不可靠（各组方差齐性对待），那么能否判断新方法吸附效果大于旧方法5（%），显著性水平α=0.05。

5，实验员测定某电子制造企业废水中Cr3+(mg/L)的含量，取了9个样品，分别对每个样品用仪器A和仪器B各测定一次，结果如下：
问两台仪器的测定性能是否有显著差异（α=0.05）。

判别分析
根据已知分类的数据建立判别函数，对未知 分类的数据进行预测和分类。
03
试验设计与统计分析关系
试验设计对统计分析影响
试验设计确定数据收集方式和样本量，直接影响 统计分析的准确性和可靠性。
合理的试验设计可以减少误差，提高统计分析的 精度和效率。
试验设计确定的因素和水平，为统计分析提供了 依据和解释。
加强数据分析和解读
运用适当的统计分析方法对数据进行分析和解读，挖掘数据背后的信 息，为食品科学研究提供有力支持。
强化交叉学科合作
加强与其他相关学科的交流和合作，共同推动食品科学研究的发展。
关注新技术新方法
关注新技术、新方法在试验设计和统计分析中的应用，及时将其引入 食品科学研究中，提高研究的质量和效率。
食品中包含多种成分，其相互作 用和影响难以预测，增加了研究 的难度。
消费者需求多样性
消费者对食品的需求和偏好日益 多样化，要求食品科学研究更加 精细化和个性化。
食品安全与营养问
题
食品安全和营养问题一直是公众 关注的焦点，对食品科学研究提 出了更高的要求。
试验设计与统计分析发展趋势
多因素试验设计
未来试验设计将更加注重多因素、多水平的 试验，以更全面地了解食品成分和加工条件 对食品品质的影响。
因素干扰的情况。
析因设计
研究多个处理因素对试验结果的 影响及其交互作用，适用于处理 因素较多且需要全面考察各因素
及其交互作用的情况。
试验设计在食品科学中应用
配方优化
感官评价
通过试验设计确定最佳原料配比和工艺参 数，优化产品配方和加工工艺，提高产品 质量和降低成本。
运用试验设计原理和方法设计和实施感官 评价试验，对食品感官属性进行客观、准 确的评价。

试验设计应保证： 试验设计应保证：
试验次数尽量少，而试验结果包含的信息尽量多，同时在 进行数据的统计分析时便于提取这些信息。 数据的统计分析方法是由试验的设计方法相应的数学模型 所决定的。 试验设计中的两个基本原理是重复和随机化。
二、试验设计举例
试验名称： “冰冻—机械”干法再生水玻璃旧砂工艺参 数优化
步骤九：输出图片 File Export page
步骤十：图片设置
所得图片：
（3）拟合曲线
软件：originpro Analysis Fit Polynomial
4、正交试验优化工艺参数 正交试验优化工艺参数
多因素多水平试验 对每个因素每个水平的相互搭配进行全面实验，是困难 的甚至是不可能的 四因素三水平，全面实验要进行34=81次 正交试验，均衡搭配，选出代表性较强的少数实验来求 得最优或较优的实验条件
正交试验设计步骤： 明确试验目的 选定因素和水平 选用正交表，做表头设计 按方案进行试验，记录试验结果 结果分析
33单因素试验单因素试验确定再生效果的影响因素确定再生效果的影响因素1旧砂含水量对再生效果的影响共5组试验旧砂含水量对脱膜率的影响冰冻温度40再生转速1000rmin再生时间8min2再生时间对再生效果的影响共4组试验再生时间对脱膜率的影响冰冻温度40旧砂含水量10再生转速1000rmin3再生设备转速对再生效果的影响共5组试验再生转速对脱膜率的影响冰冻温度40旧砂含水量10再生时间8min4旧砂冰冻温度对再生效果的影响共4组试验冰冻温度对脱膜率的影响旧砂含水量10再生转速1000rmin再生时间8min通过18组单因素试验可以确定再生效果的影响因素包括
表4 常温下水玻璃砂样受压过程中各点的应力、应变和弹性模量
（2）制图

6.试验数据的综合分析
（1）单因素试验数据的综合分析
有了单因素试验数据，可得到以下分析结果：
①通过方差分析得到因素对指标影响的显著性。
②通过回归分析得到因素对指标的影响规律。
③利用回归方程可得到最佳的参数水平及其指标值。
三、统计分析问题
（2）双因素试验数据的综合分析 有了双因素试验数据，可得到以下分析结果： ①通过方差分析得到因素及其交互作用对指标影响的 显著性。
“试验设计与统计分析”中的常见问题 四、写论文问题 1.题目要有吸引人眼球的地方 （1）试验手段先进，如：用流化床干燥大枣 （2）研究方法先进，如：用二次通用旋转组合 设计方法进行大枣干燥的研究，或大枣干燥工 艺参数的优化等。 （3）研究内容新颖，即无人进行过研究，如： 狗对牡丹花的看法。
四、写论文问题
“试验设计与统计分析”中的常见问题 三、统计分析问题 常用的统计分析方法有：方差分析，多重比较， 极差分析，回归分析，相关分析等。能得到的 分析结果如下：
三、统计分析问题 1.方差分析
以单因素试验为例，试验结果如下表。
重复次数
因素水平
1
x11 x21 … xi1
2
x12 x22 … …
…
… … … …
②通过方差分析得到因素及其交互作用对指标影响的 显著性。 ③对符合条件的正交试验数据，可进行回归分析。
三、统计分析问题
（4）多指标的参数优化
即找到一组最佳参数组合，使所有指标都较好的过程。
对于正交试验数据，可采用综合平衡法或加权综合评 分法。
对于回归试验数据，可采用加权综合评分法或主目标 优化法。
二、试验设计问题 5.回归试验
回归试验的目的是为了得到好的回归方程。有用的是 得到二次回归方程，可得到最佳参数组合。常采用二 次通用旋转组合设计，其优点是：利用回归方程预报 精度高，试验次数少。因为二次通用旋转组合设计各 因素都取5个水平，且试验点在编码空间分布合理 （分布在距中心点距离不等的3个球面上，且有星号 臂r控制回归方程的精度）。而BOX法设计，各因素 都取3个水平，分布在2个球面上，且无星号臂r控制， 回归成二次方程，不是也得是。因此，若是实际应用， 建议采用二次通用旋转组合设计。

1 Sj = ( y j1 − y j 2 ) 2 aT
（3）重复试验时，总试验误差的偏差平方和Se由两部分组成： 重复试验时，总试验误差的偏差平方和S 由两部分组成：
空列误差 Se1和重复试验误差 Se2，即
Se = Se1 + Se 2
自由度 fe等于 fe1和 fe2之和，即 之和，
fe = fe1 + fe 2
（2）计算各列偏差平方和及其自由度
b Sj = aT 1 = 12
a b
∑
k =1 2
y jk
2
a 1 − (∑ aT i = 1
T
∑
t =1
4 y it ) 2 = 16 × 3
a
∑
k =1
y jk
2
303 2 − 16 × 3
∑
k =1
y jk − 1912 . 69
S A = S1 =
1 ( 3047 . 04 + ... + 6320 . 25 ) − 1912 . 69 = 49 . 99 12
表中无空列，所以 小于S 表中无空列，所以Se1=0。但Sc/fc小于 e2/fe2， 。 因此应将S 归入试验误差的偏差平方和S 因此应将 c归入试验误差的偏差平方和 e， 则Se=Se2+Sc=67.85，fe=fe2+fc=20。对各因素 ， 。 进行显著性检验。结果表明，A、B和D因 进行显著性检验。结果表明， 、 和 因 素都是显著性因素。显然最优组合应取A 素都是显著性因素。显然最优组合应取 3, B2 和D3 ，而对于不显著因素 取适当水平。 而对于不显著因素C取适当水平 取适当水平。 假定从节约出发，选定C 假定从节约出发，选定 3 , 则本试验最优组 合为

第一章食品试验设计1.什么叫试验误差？试验误差的主要来源有哪些？2.如果设计优良，试验误差是可以消灭的。

（〕3.试验误差可计算出来，因而试验的准确度也可以估测。

（）4.试验精确度越高，其准确度亦越高。

（）5.在拟订试验方案时，必须应用唯一差异的原则。

这里的“唯一差异”是指的什么？6.天然色素丹参红色素提取工艺条件的优化试验中，常规提取溶剂酒精浓度为85%，原料固液比（乙醇：丹参粉）为5，提取时间为1小时。

请你设计一个三因素三水平共27个处理的三次重复试验，目的是优化丹参红色素提取工艺。

7.在试验过程中，供试材料不均匀，有差异时，如何安排试验？8.请简述食品试验的基本要求和注意事项？9.试验方案是指_____________________________________________。

10.准确度是指_________________________________________________。

11.精确度是指__________________________________________________。

12.要正确地制定一个试验方案，必须作到研究目的明确，处理水平简明合理，并必须在所比较的处理之间应用（）原则。

A.设立对照B.唯一差异C.全面设施D.相差等距或等比例13.有一加热时间和加热温度对番茄果胶酶活性影响的试验，温度有45、50、55、60℃4个水平，时间有30、60分钟两个水平，试写出处理组合数及各处理组合名称。

14.试验因素对所研究的性状起增进或减少的作用。

称为。

15.试验水平是指__________________________________________________。

16.什么叫试验单元、单位？17.何谓试验因素？作为试验因素须具备哪些条件？18.多因素试验是指________________________________________。

19.试验的水平和处理在所有试验中都是一致的。

课堂内外小学数学教学中作业优化设计策略分析吴文萍（安徽省安庆市岳西县实验小学,安徽 安庆 246600）摘要：优化作业设计是小学数学教学中面临的最重要的问题，受传统教育教学理念的影响，小学数学作业设计一直存在着一些比较明显的问题，如何进一步的完善作业设计策略，提高作业设计的质量和效果，成为目前最为重要的教学任务之一。

本文从传统教育教学理念下的小学数学作业设计存在的问题入手，简要的分析了小学数学作业优化设计策略。

关键词：小学数学；作业优化设计；问题；策略一、传统教育理念下小学数学作业存在的问题首先，从教师方面讲，传统应是教育理念下教师在小学数学作业布置的过程中并没有充分的关注小学生的学习兴趣等客观因素；只是单纯的根据教材内容和课后作业为学生布置相关的课业，没有考虑学生的承受能力；因此会出现一些“重视数量，轻视质量”的作业安排情况。

教师过于重视书本中的“写”作业，而忽略了学生学习能力、实践能力等方面的培养。

此外，传统应试教育理念数学作业设计的形式过于单一，而且很多教师为了提升学生的某些能力，采用比较极端的方式，如单纯的采用“题海”战术来提升学生的计算能力，忽略了课外作业的适度、适量的原则，学生需要用大量的休息时间来“应付”大量的数学作业，此种情况下学生很容易就会产生疲劳感。

这不仅影响了小学生的数学学习兴趣的提升，而且对学生的良好学习习惯和生活习惯的形成也产生了极为不利的影响。

其次，小学生数学作业还有一部分来自于家长；很多家长在没有与教师及时沟通的情况下，盲目的为孩子报课外辅导班，名义上是为了提高学生兴趣，拓展学生学习思维，实则增加了学生的课业负担，而且对学生的健康成长也产生了极为不利的影响。

二、小学数学教学中作业优化设计策略分析《国家中长期教育改革发展规划纲要》中明确指出要将减负落实到教育教学的每一个环节。

尤其是在数学作业设计方面，我们在进行数学作业设计师要从学生的实际出发，遵循数学作业设计的原则，争取能够为学生留出更多的时间去参与一些数学实践活动，在实践中巩固课堂知识，在实践中提升应用能力。