下载文档原格式
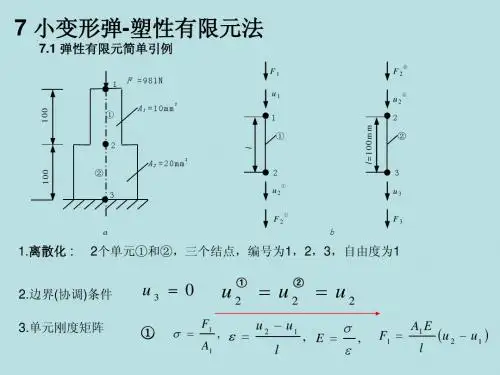
§4.3 弹塑性增量分析的有限元格式 一、弹塑性问题的增量方法材料和结构的弹塑性行为与加载及变形历史有关。
在进行结构的弹塑性分析时，通常将载荷分成若干个增量，然后对于每一载荷增量，将弹塑性方程线性化，从而使弹塑性分析这一非线性问题分解为一系列问题。
假设对于时刻t 的载荷和位移条件的位移t i u ，应变t ij ε和应力t ij σ已经求得。
当时刻过渡到t t + ，载荷和位移有一增量，t tti i iF F F +=+ （在v 内） t tti i i T T T +=+ （在S σ内） （1）t tti i i u u u +=+ （在u S 内）现要求解t t + 时刻的位移，应变和应力t tt i i i u u u +=+t tt ij ij ij εεε+=+ （2）t tt ij ij ij σσσ+=+它们应满足的方程和边界条件是：平衡方程,,0ttij j ij j i i F F σσ+++= （在v 内） （3） 应变和位移关系 ,,,,11()()22t t t ij ij i j j i i j j i u u u u εε+=+++ （在v 内） （4） 应力和应变关系epij ijkl kl D τσε= （t t ττ≤≤+ ） （在v 内） （5）边界条件tti i i i T T T T +=+ （在S σ上） （6） t ti i i i u u u u +=+ （在u S 上） （7）且 t ti ij j T n σ=i ij j T n σ= （8）二、增量有限元格式增量形式的虚位移原理：如果时刻t t + 的应力tij ij σσ+ 和体积载荷ti i F F + 及边界载荷ti i T T + 满足平衡条件，则此力系在满足几何协调条件的虚位移()i u δ [在v 内，,,1()()2ij i j j i u u δεδ=+ ，在u S 上，()i u δ =0]上的总虚功等于0，即()()()()()()0t tt ij ij ij i i i i i i vvS dv F F u dv T T u ds σσσδεδδ+-+-+=⎰⎰⎰ （9）将（5）式代入，可得：()()()()()()ep ijkl kl ij i i i i vvS tttij ij i i i i vvS D dv F u dv T u dsdv F u dv T u dsσστεδεδδσδεδδ--=-++⎰⎰⎰⎰⎰⎰（10）其矩阵形式为：()()()()()()T T T ep vvS t ttT T T vvS D dv u Fdv u Tds dv u Fdv u Tdsσστδεεδδδεσδδ--=-++⎰⎰⎰⎰⎰⎰（11）基于增量形式虚位移原理有限元表达格式的建立步骤和一般全量形式完全相同，eu N a =（12）eB a ε=（13）代入（11）式，并利用虚位移任意性，有ep K a Q τ=（14）ep K τ、a、Q分别是系统的弹塑性刚度矩阵、增量位移矢量和不平衡力矢量。
有限元与数值方法-讲稿19弹塑性增量有限元分析课件第一篇：有限元与数值方法-讲稿19 弹塑性增量有限元分析课件材料非线性问题有限元方法教学要求和内容1.掌握弹塑性本构关系和塑性力学的基本法则；2.掌握弹塑性增量分析的有限元格式；3.学习常用非线性方程组的求解方法：（1）直接迭代法；（2）Newton-Raphson 方法，修正的N－R 方法；（3）增量法等。
请大家预习，争取对相关内容有大概的了解和把握。
弹塑性增量有限元分析一．材料弹塑性行为的描述弹塑性材料进入塑性的特点：存在不可恢复的塑性变形；卸载时：非线性弹性材料按原路径卸载；弹塑性材料按不同的路径卸载，并且有残余应变，称为塑性应变。
1．单向加载1）弹性阶段: 卸载时不留下残余变形;2）初始屈服：σ=σs3）强化阶段：超过初始屈服之后,按弹性规律卸载，再加载弹性范'为相继屈服应力。
围扩大：σ'>σss，σs 4）鲍氏现象（Bauschinger）：二．塑性力学的基本法则1．初始屈服准则：F0(σij,k0)=0已经建立了多种屈服准则：（1）V.Mises 准则：F0(σij,k0)=f(σij)-k0=01(第二应力不变量),k0=(σs0)231偏应力张量：sij=σij-δijσm,平均应力：σm=(σ11+σ22+σ22)31f(σij)=sijsij=J22（2）Tresca准则（最大剪应力准则）：F0(Sij)=τmax-τs=02．流动法则V.Mises 流动法则：dε=dλpij∂F(σij,k0)∂σijpij=dλ∂f(σij)∂σij，dλ>0 待定有限量塑性应变增量 dε沿屈服面当前应力点的法线方向增加。
因此，称为法向流动法则。
3．硬化法则：（1）各向同性硬化：F(σij,k)=f(σij)-k=012p2pppk=σs(ε),ε=⎰dεijdεij等效塑性应变，可由单拉试验确定。
33（2）运动硬化法则：* Prager运动硬化准则；（3）混合硬化法则： Zeigler修正的运动硬化准则。
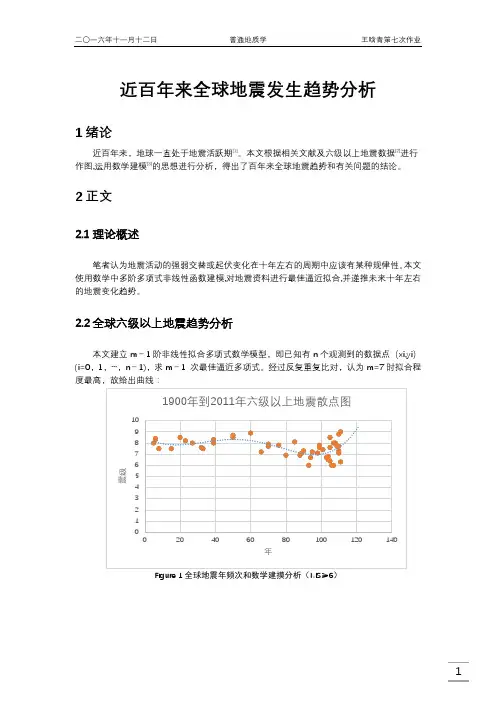
近百年来全球地震发生趋势分析1绪论近百年来，地球一直处于地震活跃期[1]。
本文根据相关文献及六级以上地震数据[2]进行作图,运用数学建模[3]的思想进行分析，得出了百年来全球地震趋势和有关问题的结论。
2正文2.1理论概述笔者认为地震活动的强弱交替或起伏变化在十年左右的周期中应该有某种规律性。
本文使用数学中多阶多项式非线性函数建模,对地震资料进行最佳逼近拟合,并递推未来十年左右的地震变化趋势。
2.2全球六级以上地震趋势分析本文建立m－1阶非线性拟合多项式数学模型，即已知有n个观测到的数据点（xi,yi）(i=0，1，…，n－1)，求m－1 次最佳逼近多项式。
经过反复重复比对，认为m=7时拟合程度最高，故给出曲线：Figure 1全球地震年频次和数学建摸分析（MS≥6）2.3震级与死亡人数的关系分析Figure 2全球地震死亡人数和数学建摸分析（MS≥6）3结论在百年中，地震的震级在时间轴上波动，且波动幅度和周期有增大的趋势，曲线的平衡轴在7.5~8.0级之间。
根据多项式曲线的对称原则，下一个波峰震级在九级左右，在十年内不会出现。
未来十年地震强度会有增大的趋势。
而地震的死亡人数在7.8级出项峰值，所以我们应该重点做好8级地震的抗震工作。
对地震预报可行性的分析1绪论中国邻近环太平洋地震带和地中海—印尼地震带的交界地区[4]，地震频繁。
因此，能否对地震做出预报事关国家人民的生命财产安全。
现阶段的地震预报分为三种：基于前兆现象的经验预报和统计预报，基于物理规律的数值预报[5]，它们对地震的预报由于自身的原理、方法不同导致了预报的范围、准确性都有很大不同。
2对三种预报准确性的分析经验预报是指，根据所观测的物理量化学量可以测量的数据，分析其趋势（如曲线上升、下降、突跳等），综合各种“异常”（宏观异常：动物反应等；微观异常：水温水位，地磁，形变，地倾斜，空气或地下水化学量等等[6]），从而对某个片区进行预报。
统计预报同样是根据前兆观测得到的经验，通过统计检验的方式，得到地震发生的规律，从而对地震进行预报。
三维边坡稳定弹塑性有限元分析与评价边坡的稳定性对环境的稳定性与可持续发展具有重要意义，而三维边坡稳定弹塑性有限元分析与评价技术则可更有效地维护边坡稳定性。
本文重点介绍了三维边坡稳定弹塑性有限元分析与评价，分析其基本原理、数学模型、常见应用等内容，并针对有限元分析技术存在的广泛应用、空间技术局限性等问题，提出若干改进的方法和技术。
一、三维边坡稳定弹塑性有限元分析学术回顾三维边坡稳定弹塑性有限元分析是以数学模型为基础，运用有限元法进行地质边坡稳定性的分析与评价的技术，结合有限元求解，分析边坡的稳定性。
其基本原理是：当地质边坡受力时，其受力状态下的变形可以用位移量、应变量或应力量来描述，而每一点受力状态的变形均可用一组局部坐标表示，当受力后的变形状态下的变形强度比受力前的状态还要低时，就可以判断为无滑移状态，也就是稳定。
三维边坡稳定弹塑性有限元分析迎合了边坡稳定性分析中几何形态复杂、多尺度、考虑材料弹塑性、力学性质复杂等复杂性因素，精确地模拟了边坡稳定性分析过程中的复杂动力学过程。
二、常见应用三维边坡稳定弹塑性有限元分析技术有多种应用，主要应用于岩土体结构的受力数值模拟、岩土体的变形和失稳的有限元模拟和分析、及岩土体稳定性的评价。
在岩土体受力数值模拟方面，三维边坡稳定弹塑性有限元分析技术可以通过计算机化的方法，对边坡受力数值模拟和变形和失稳的有限元模拟分析，分析受力后的位移、变形和强度，从而更好地评价岩土体结构的受力稳定性。
此外，三维边坡稳定弹塑性有限元分析技术可以运用于地质模型结构的有限元模拟，对模型进行受力和变形分析，验证建模中存在的错误，并对工程建设中可能出现的风险进行预测，提出具体意见。
三、改进思路物理模拟的三维边坡稳定弹塑性有限元分析具有计算量大，计算时间较长，技术局限性等缺点，因此，提出若干改进措施可以有效改善这些问题，提高有限元分析技术的精度和应用效果：（1）布置边坡滑移状态时，尽量采用体单元网格布置，而不是采用梯度布置的网格。
基于D-P准则的三维弹塑性有限元增量计算的有效算法A practical3D ela sto2pla stic incremental method in FEMba sed on D-P yield criteria杨 强,陈 新,周维垣(清华大学水利系,北京 100084)摘 要:针对岩土材料常用的D-P准则,提出了一种新的增量分析方法,不用形成弹塑性增量矩阵,直接导出了符合正交流动法则的转移应力的解析解。
该方法无论是对小步长还是大步长加载均有良好的收敛性。
当采用精细的步长划分时,它就是严格意义上的理想弹塑性增量计算。
在大步长情况下,在收敛域内最大载荷低于结构真实的极限承载力;对应的应力场是一个静力容许应力场;同时由于正交流动法则在平均意义下得到满足,收敛域内最大载荷接近结构真实的极限承载力。
按此法所得结果接近真解且偏于安全。
将整个计算模型装入三维非线性有限元程序TFI NE中,对某拱坝进行了超载分析。
关键词:转移应力;极限载荷;点安全度中图分类号:T U452 文献标识码:A 文章编号:1000-4548(2002)01-0016-05作者简介:杨 强(1964-),男,云南人。
1988年在清华大学获硕士学位,1996年在奥地利Innsbruck大学获博士学位,现为清华大学水利系教授。
主要从事水工结构及岩石力学方面的研究工作。
Y ANG Qiang,CHE N X in,ZH OU Wei2yuan(Department of Hydraulic Engineering,Tsinghua University,Beijing100084,China)Abstract:In this paper,focused on popularly used D-P yield criteria in geomaterials,a new incremental method in which the stresses to be trans2 ferred according to normal flow rule are directly derived without forming elasto2plastic increment matrix,was proposed.This method converges for either small load steps or large load steps.When very small load steps are used,the method is equivalent to standard elasto2plastic incremental method.When large load steps are used,the maximum load applied is lower than limit load in structure,the calculated stress field is an static ad2 missible one.As normal flow rule is satisfied in average,the maximum load is close to limit load.The soltion calculated by the method is on the safe side and close to real solution.The method was embedded into a3D nonlinear FEM software named TFINE,and overloading analysis was performed on an arch dam.K ey words:the stresses to be transferred;normal flow rule;limit load1 引 言Ξ岩土材料具有很复杂的本构特性,如各向异性、硬化、软化等,目前描述岩土材料的本构模型非常多。
但在实际工程三维有限元计算分析中,尤其是在岩体工程里,大量使用的仍是最简单D-P准则及理想弹塑性分析。
其主要原因是参数选取不易。
如在二滩高拱坝建设中,做了大量坝肩岩体现场大型抗剪试验,但具体到某一岩级,试验点数仍然很有限,且离散性很大。
很难完全依赖试验确定参数,一般都要进行工程类比,对中、小工程工程类比更是参数确定的主要手段。
最终一般只能给出岩体的抗剪参数f,c值。
在这种情况下,从工程实用角度来说,追求本构关系的精致、完备并无太多实用意义。
相对而言,在岩土工程三维非线性有限元分析里,计算收敛性是一个较大的问题。
弹塑性增量计算要采用精细的步长划分,才能确保计算收敛到正确解。
在岩土工程,尤其是岩体工程里,荷载量级都很大,如高拱坝对水荷载的极限承载力可达上亿吨,而这对两岸高陡边坡所承受的的自重荷载来说,还只是一个小数,又如高地应力区大型地下洞室、高边坡(如三峡船闸高边坡)开挖过程中的释放荷载量级也十分巨大。
若采用精细的步长划分,计算量将很大。
岩体地质构造复杂,三维网格划分时经常会有畸形单元。
由于地址缺陷或加固措施导致相邻单元材料性质差异过大,再加上高水平的荷载,各种因素交互影响,使得在计算过程中,经常出现局部发散现象,使得增量计算难以进行下去,最终结果可信度低,也难以从计算结果判断何时结构丧失稳定性。
而对岩土工程来说,往往更关注结构的稳定性和极限承载力,而非应力和位移分布。
Ξ基金项目:国家自然科学基金资助项目(59879005);清华大学基础研究基金资助项目收稿日期:2001-04-12 第24卷 第1期岩 土 工 程 学 报V ol.24 N o.1 2002年 1月Chinese Journal of G eotechnical Engineering Jan., 2002 本文针对目前三维非线性有限元分析岩土材料常用的D -P 准则,提出了一种新的增量分析方法,它直接导出了符合正交流动法则的转移应力的解析解,不用形成弹塑性增量矩阵。
该方法无论是对小步长还是大步长加载均有良好的收敛性。
当采用精细的步长划分时,它就是严格意义上的理想弹塑性增量计算。
当采用大步长增量计算,所得到是在平均意义上符合正交流动法则的一个静力容许应力场;在收敛域内,所能施加的最大荷载接近极限载荷的下限。
2 转移应力的解析解在三维有限元弹塑性增量分析里,D -P 准则由于简单实用,且和当前地质方面所能提供参数相适应,一直是目前应用最广的岩土材料屈服准则,其形式为f =αI 1+J 2-k ≤0(1)式中 J 2=16[(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2],I 1=σ1+σ2+σ3,其中σ1,σ2,σ3为主应力。
α和k 可通过拟合莫尔-库仑准则而得。
例如,在π平面上,若D -P 准则为库仑六边形的外接园,则α=2sin φ3(3-sin φ),k =6c cos φ3(3-sinφ)(2)式中 φ和c 为材料的摩擦角和粘聚力。
设某一高斯点在某一加载步或迭代步前初始应力为σ0且满足f (σ0)≤0。
对某一个加载步或迭代步,由位移法求得该点应变增量为Δε,它对应于弹性试应力σ1=σ1ij =σ0+D :Δε,这里D 为弹性张量;若f (σ1)>0,则需进行应力调整。
若此加载步或迭代步中塑性应变增量为Δεp,则调整后的应力为σ=σij =σ0+D :(Δε-Δεp)=σ1-D :Δεp。
将正交流动法则d εp=d λ5f 5σ近似写成增量形式Δεp =Δλ5f 5σ,并以σ1确定5f Π5σ的代表值。
则由条件f (σ)=0,σ=σ1-ΔλD :5f 5σσ=σ1(3)即可确定调整后应力σ=σij =(1-n )σ1ij +p δij (4)这里n =wμJ 2,p =-mw +13nI 1,m =α(3λ+2μ),w =f3αm +μ(5)其中J 2,I 1,f 均由σ1确定。
λ,μ为拉梅常数,即λ=E ν(1+ν)(1-2ν),μ=E2(1+ν)(6)式中 E ,ν为杨氏模量和泊松比。
容易证明由式(4)确定的调整后应力σ必在屈服面上,即f (σ)=0。
故对每个增量步或迭代步,应力转移值为Δσ=σ1-σ=n σ1ij -p δij (7) 求得由式(7)确定的转移应力Δσ后,可采用最普通的常刚度迭代进行应力转移计算。
该方法避免了复杂的塑性矩阵的运算,直接求得满足正交流动法则的应力转移值。
显然当采用精细的步长划分时,正交流动法则d εp=d λ(5f Π5σ)得到充分满足,它就是严格意义上的理想弹塑性增量计算。
以σ1确定5f Π5σ对计算收敛起到重要作用,此时转移应力的方向指向屈服锥体的中心线,所以调整后应力总能退回到屈服面上来。
若以σ0确定5f Π5σ,如果σ1和σ0相差较大,则有可能调整后应力无法退回到屈服面上来。
这实际上也是一般弹塑性计算当增量步过大就不收敛的重要原因之一。
一般弹塑性计算也不进行校核。
本文建议的方法在任何步长下都能确保调整后应力在屈服面上。
大量的数值计算表明该方法具有良好的收敛性,所以可以用计算是否收敛来作为整体结构是否失稳的判据。
在大步长情况下求得的应力场与精细的步长划分下的所得是有差异的。
我们可以从极限承载力的角度来探讨一下这个问题。
在比例加载下,结构所能承受的最大荷载为极限承载力。
在精细的步长划分下,理想弹塑性增量计算的最大荷载就是严格意义上的极限承载力。
极限分析的下限定理认为:“一个满足平衡条件并且到处都不破坏材料屈服条件的应力场,是一个静力容许应力场;跟静力容许应力场对应的外荷载是极限荷载的下限;最高的下限便是极限荷载”。
显然,在大步长情况下,在收敛域内最大载荷低于结构真实的极限承载力;对应的应力场是一个静力容许应力场;同时由于正交流动法则在平均意义下得到满足,收敛域内最大载荷接近结构真实的极限承载力。
所以按此法所得的极限承载力接近真解且偏于安全。
3 其他考虑岩土材料为低抗拉材料,故还应考虑抗拉条件:σ1≤σt ,σ2≤σt ,σ3≤σt(8)式中 σt 为材料单轴抗拉强度。
在程序流程上,首先判断抗拉条件是否满足,若不满足,则调整应力满足之;其次再按D -P 准则判断调整应力。
整个计算模型被装入三维非线性有限元程序TFI NE 里。
在TFI NE 里,材料有三种破坏模式Ξ:71Ξ对理想弹塑性模型而言,屈服即为破坏。
第1期杨 强,等1基于D -P 准则的三维弹塑性有限元增量计算的有效算法(1)剪切破坏(相对于D -P 准则,式(1));(2)拉坏(式(8));(3)拉-剪破坏,即材料既拉坏又剪坏。
TFI NE 的塑性屈服区3种图案如图1,分别代表这三种破坏模式。
