角平分线的性质定理及判定定理

4321N M A B O D P P CA B M N M N AB DC P ED A BC 角平分线的性质与判定一、知识梳理：1．角平分线的性质定理：角平分线上的点到角两边的距离相等.2．角平分线的判定定理：角的内角到角两边距离相等的点在这个角的平分线上.3．有角平分线时常常通过下列几种情况构造全等三角形.二、典型例题：例１、如图，已知OD 平分∠AOB ，在OA 、OB 边上截取OA ＝OB ，PM ⊥BD ，PN ⊥AD .求证：PM ＝PN及时练习：1．如图，CP 、BP 分别平分△ABC 的外角∠BCM 、∠CBN .求证：点P 在∠BAC 的平分线上.2．如图，BD 平分∠ABC ，AB ＝BC ，点P 是BD 延长线上的一点，PM ⊥AD ，PN ⊥CD .求证：PM ＝PN例２、如图，已知四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于点E ，且AE ＝12(AB ＋AD )，如果 ∠D ＝120°，求∠B 的度数.及时练习：D CA B D F E BA CD E C A B1．如图，在△ABC 中，CD 平分∠ACB ，AC ＝5，BC ＝3.求ACD CBD S S ∆∆.2．在四边形ABCD 中，已知AB ＝a ，AD ＝b .且BC ＝DC ，对角线AC 平分∠BAD ，问a 与b 的大小符合什么条件时，有∠B ＋∠D ＝180°，请画图并证明你的结论.例3、如图，在△ABC 中，∠BAC ＝90°,AB ＝AC ，BE 平分∠ABC ，CE ⊥BE .求证：CE ＝12BD.及时练习：1．如图，已知AC ∥BD ，EA 、EB 分别平分∠CAB 、∠DBA ，CD 过点E ，求证：AB ＝AC ＋BD .2．如图，在△ABC 中，∠B ＝60°，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F .⑴请你判断FE 和FD 之间的数量关系，并说明理由； ⑵求证：AE ＋CD ＝AC .第1题图D C B A第2题图D B C A E P 第3题图Q S R P B A C 第4题图E F B D A C 第5题图E B C A第6题图F E D P A B C 第7题图P A B C E F 第8题图D A B C E 第9题图E D C AB 第10题图K N M QC B A三、课堂练习：1．如图，在Rt △ABC 中，∠C ＝90°，BD 平分∠ABC 交AC 于D ，若CD ＝n ，AB ＝m ，则△ABD 的面积是（ ） A ．13mn B ．12mn C ． mn D ．2 mn2．如图，已知AB ＝AC ，BE ＝CE ，下面四个结论：①BP ＝CP ；②AD ⊥BC ；③AE 平分∠BAC ；④∠PBC ＝∠PCB .其中正确的结论个数有（ ）个A ． 1B ．2C ．3D ．43．如图，在△ABC 中，P 、Q 分别是BC 、AC 上的点，作PR ⊥AB ，PS ⊥AC ，垂足分别是R 、S .若AQ ＝PQ ，PR ＝PS ，下列结论：①AS ＝AR ；②PQ ∥AR ；③△BRP ≌△CSP .其中正确的是（ ）A ． ①③B ．②③C ．①②D ．①②③4．如图，△ABC 中，AB ＝AC ，AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，则下列四个结论中：①AD 上任意一点到B 、C 的距离相等；②AD 上任意一点到AB 、AC 的距离相等；③AD ⊥BC 且BD ＝CD ；④∠BDE ＝∠CDF .其中正确的是（ ）A ．②③B ．②④C ．②③④D ．①②③④5．如图，在Rt △ABC 中，∠ACB ＝90°，∠CAB ＝30°，∠ACB 的平分线与∠ABC 的外角平分线交于E 点，则∠AEB 的度数为（ ）A ．50°B ．45°C ．40°D ．35°6．如图，P 是△ABC 内一点，PD ⊥AB 于D ，PE ⊥BC 于E ，PF ⊥AC 于F ，且PD ＝PE ＝PF ，给出下列结论：①AD ＝AF ；②AB ＋EC ＝AC ＋BE ；③BC ＋CF ＝AB ＋AF ；④点P 是△ABC 三条角平分线的交点.其中正确的序号是（ ）A ．①②③④B ．①②③C ．①②④D ．②③④7．如图，点P 是△ABC 两个外角平分线的交点，则下列说法中不正确的是（ ）A ．点P 到△ABC 三边的距离相等B ．点P 在∠ABC 的平分线上 C ．∠P 与∠B 的关系是：∠P ＋12∠B ＝90°D ．∠P 与∠B 的关系是：∠B ＝12∠P8．如图，BD 平分∠ABC ，CD 平分∠ACE ，BD 与CD 相交于D .给出下列结论：①点D 到AB 、AC 的距离相等；②∠BAC ＝2∠BDC ；③DA ＝DC ；④DB 平分∠ADC .其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个9．如图，△ABC 中，∠C ＝90°，AD 是△ABC 的角平分线，DE ⊥AB 于E ，下列结论中：①AD 平分∠CDE ；②∠BAC ＝∠BDE ；③ DE 平分∠ADB ；④AB ＝AC ＋BE .其中正确的个数有（ ）A ．3个B ．2个C ．1个D ．4个10．如图，已知BQ 是△ABC 的内角平分线，CQ 是△ACB 的外角平分线，由Q 出发，作点Q 到BC 、AC 和AB 的垂线QM 、QN 和QK ，垂足分别为M 、N 、K ，则QM 、QN 、QK 的关系是_________F B D EC A O F ED A B C l 1l 2l 3第1题图第3题图D C A B P 第4题图F GE P A B C D 第5题图E O D B A C GP F E D C B A 11．如图，AD 是∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，且DB ＝DC .求证：BE ＝CF .12．如图，在△ABC 中，AD 是∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 于点F .求证：AD ⊥EF .四、巩固提高：1．如图，直线l 1、l 2、l 3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有（ ）A ．一处B ．二处C ．三处D ．四处2．已知Rt △ABC 中，∠C ＝90°，AD 平分∠BAC 交BC 于D ，若BC ＝32，且BD :CD ＝9:7，则D 到AB 边的距离为（ ）A ．18B ．16C ．14D ．123．如图，△ABC 中，∠C ＝90°，AD 是△ABC 的平分线，有一个动点P 从A 向B 运动.已知：DC ＝3cm ，DB ＝4cm ，AD ＝8cm .DP 的长为x (cm )，那么x 的范围是__________4．如图，已知AB ∥CD ，PE ⊥AB ，PF ⊥BD ，PG ⊥CD ，垂足分别为E 、F 、G ，且PF ＝PG ＝PE ，则∠BPD ＝__________5．如图，已知AB ∥CD ，O 为∠CAB 、∠ACD 的平分线的交点，OE ⊥AC ，且OE ＝2，则两平行线AB 、CD 间的距离等于__________6．如图，AD 平分∠BAC ，EF ⊥AD ，垂足为P ，EF 的延长线于BC 的延长线相交于点G .求证：∠G ＝12(∠ACB －∠B )QP C B A 7．如图,在△ABC 中,AB ＞AC ,AD 是∠BAC 的平分线,P 为AC 上任意一点.求证:AB －AC ＞P B －P C.8．如图，在△ABC 中，∠BAC ＝60°，∠ACB ＝40°，P 、Q 分别在BC 、AC 上，并且AP 、BQ 分别为∠BAC 、∠ABC 的角平分线上.求证：BQ ＋AQ ＝AB ＋BP。

第一部分：知识点回顾1、角平分线：把一个角平均分为两个相同的角的射线叫该角的平分线；2、角平分线的性质定理：角平分线上的点到角的两边的距离相等：①平分线上的点；②点到边的距离；3、角平分线的判定定理：到角的两边的距离相等的点在角平分线上第二部分：例题剖析例1. 已知：在等腰Rt Rt△△ABC 中，AC=BC AC=BC，，∠C=90°，AD 平分∠平分∠BAC BAC BAC，，DE DE⊥⊥AB 于点E ，AB=15cm AB=15cm，，（1）求证：）求证：BD+DE=AC BD+DE=AC BD+DE=AC．．（2）求△）求△DBE DBE 的周长．的周长．例2. 如图，∠如图，∠B=B=B=∠C=90°，∠C=90°，∠C=90°，M M 是BC 中点，中点，DM DM 平分∠平分∠ADC ADC ADC，求证：，求证：，求证：AM AM 平分∠平分∠DAB DAB DAB．．例3. 如图，已知△如图，已知△ABC ABC 的周长是2222，，OB OB、、OC 分别平分∠分别平分∠ABC ABC 和∠和∠ACB ACB ACB，，OD OD⊥⊥BC 于D ，且OD=3OD=3，△，△，△ABC ABC 的面积是多少？的面积是多少？角平分线的性质定理和判定第三部分：典型例题例1、已知：如图所示，CD ⊥AB 于点D ，BE ⊥AC 于点E ，BE 、CD 交于点O ，且AO 平分∠BAC ，求证：OB=OC ．【变式练习】如图，已知∠1=∠2，如图，已知∠1=∠2，P P 为BN 上的一点，PF⊥BC 于F ，PA=PC PA=PC，求证：∠PCB+∠BAP=180º，求证：∠PCB+∠BAP=180º，求证：∠PCB+∠BAP=180º例2、已知：如图，∠B=∠C=90°，M 是BC 的中点，DM 平分∠ADC ． （1）若连接AM ，则AM 是否平分∠BAD ？请你证明你的结论；？请你证明你的结论； （2）线段DM 与AM 有怎样的位置关系？请说明理由．有怎样的位置关系？请说明理由．（3）CD 、AB 、AD 间？直接写出结果【变式练习】如图，△如图，△ABC ABC 中，中，P P 是角平分线AD AD，，BE 的交点．的交点． 求证：点P 在∠在∠C C 的平分线上．21NPF CBA【变式练习】如图，D 、E 、F 分别是△ABC 的三条边上的点，CE=BF ，△DCE 和△DBF 的面积相等．求证：AD 平分∠BAC ．例3.如图，在△ABC 中，BD 为∠ABC 的平分线，DE ⊥AB 于点E ，且DE=2cm ，AB=9cm ，BC=6cm ，求△ABC 的面积．的面积．第四部分：思维误区第五部分：方法规律第七部分：巩固练习DAD M A B C N P E D B C A E F ADP7．如图，如图，已知在△已知在△ABC 中，90C Ð=，点D 是斜边AB 的中点，2AB BC =，DE AB ^ 交AC 于E ．求证：BE 平分ABC Ð．8、如图，∠B =∠C =90°，M 是BC 的中点，DM 平分∠ADC ，求证：AM 平分∠DAB. 9.如图，在∠AOB 的两边OA ，OB 上分别取OM=ON ，OD=OE ，DN 和EM 相交于点C ． 求证：点C 在∠AOB 的平分线上．上．第八部分：中考体验ＢＤＡＥＣA ． 1B ． 2C ． 3D ． 4A ． 11 B ． 5.5 C ． 7D ． 3.5 3．（2010•鄂州）如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 交AC 于点F ．S △=7，A ． 4B ．3 C ．6 D ．5 间的距离为间的距离为 _________ ．2．（2011•恩施州）如图，AD △ABC DF AB F DE=DG △ADG △AED。

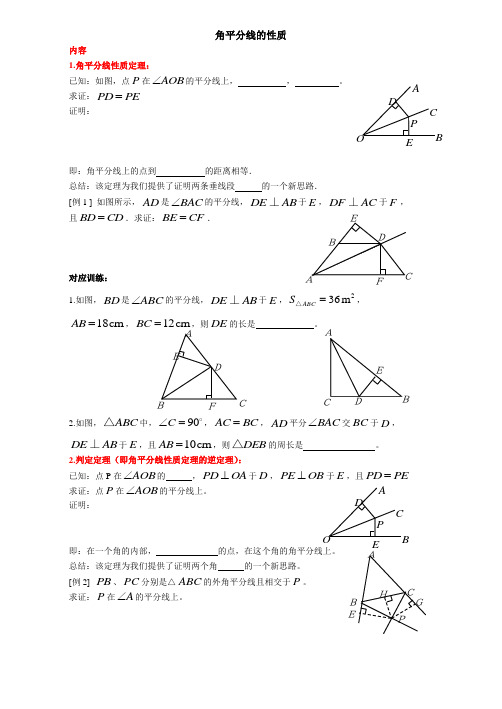
角平分线的性质内容1.角平分线性质定理：已知：如图，点P 在AOB ∠的平分线上， ， 。

求证：PD PE =证明：即：角平分线上的点到 的距离相等．总结：该定理为我们提供了证明两条垂线段 的一个新思路．[例1 ] 如图所示，AD 是BAC ∠的平分线，DE AB ⊥于E ，DF AC ⊥于F，且BD CD =．求证：BE CF =． 对应训练：1.如图，BD 是ABC ∠的平分线，DE AB ⊥于E ，236m ABCS =△，18cm AB =，12cm BC =，则DE 的长是。

2.如图，ABC △中，90C ∠=，AC BC =，AD 平分BAC ∠交BC 于D ，DE AB ⊥于E ，且10cm AB =，则DEB △的周长是。

2.判定定理（即角平分线性质定理的逆定理）： 已知：点P 在AOB ∠的 ，PDOA ⊥于D ，PE OB ⊥于E ，且PD PE =求证：点P 在AOB ∠的平分线上。

证明：即：在一个角的内部， 的点，在这个角的角平分线上。

总结：该定理为我们提供了证明两个角 的一个新思路。

[例2]PB 、PC 分别是△ABC 的外角平分线且相交于P 。

求证：P 在A ∠的平分线上。

A BC DEPOＡＢ ＥＧ Ｃ ＨＰA B CD E PO对应训练： 如图，已知在△ABC 中，90C ∠= ，点D 是斜边AB 的中点，2AB BC =，DE AB ⊥交AC 于E ． 求证：BE 平分ABC ∠．3. 如图5，已知等腰三角形ABC △中，90A ︒∠=，B ∠的平分线交AC 于点D ， 过点C 作BD 的垂线交BD 的延长线于点E ．求证：BD =点拨：“角平分线 + 垂线”构造全等三角形或等腰三角形课堂练习1..如图，在ABC △中，AB AC =，AD 是ABC∠的角平分线，DE AB ⊥，DF AC ⊥，垂足分别是E ，F ，则下列四个结论：①AD 上任意一点到点C ，点B 的距离相等； ②AD 上任意一点到AB ，AC 的距离相等； ③BD CD =，AD BC ⊥； ④BDE CDF ∠=∠．其中，正确的是2.如图，在△ABC 中，∠BAC ，∠BCA 的平分线相交于点O ，过点O 作DE ∥AC ，分别交AB ，BC 于点D ，E ．试猜想线段AD ，CE ，DE 的数量关系， 并说明你的猜想理由。

角平分线的性质和判定一、基础知识回顾。

角平分线的性质： 角平分线的判定：一、分线的判定定理角平分线的判定：到角两边距离相等的点在 。

如图：∵P D ⊥OA,PF ⊥OB ，PD=PE ，∴P 在∠AOB 的平分线上，或（∠AOP=∠BOP ）1、如图，90C ∠=︒，AD 平分CAB ∠，BD=2CD ，BC=9，求点D 到AB 的距离。

D C BA2、如图，求作到三条直线距离相等的所有点。

3、如图，90B C ∠=∠=︒，M 是BC 的中点，DM 平分ADC ∠，求证：AM 平分DAB ∠。

MDCBA4. 如图所示，已知BE ⊥AC 于E ，CF ⊥AB 于F ，BE 、CF 相交于点D ，若BD =CD . 求证：AD 平分∠BAC .5、如图，DE AB ⊥，DF AC ⊥，DE=DF ，求证：GE=GF 。

FGDCBAE6、如图，CD AB ⊥，BE AC ⊥，OB OC =，求证12∠=∠。

O21A B CDE7、如图，90C ∠=︒，AD 是BAC ∠的平分线，DE AB ⊥，BD=DF ，求证：CF=EB 。

FD C BAE8 如图，BE=CF ，BE ⊥AC 于F ，CE ⊥AB 于E,BF 和CE 交于点D ，求证：AD 平分∠BAC.9.如图在△ABC 中，∠B=∠C ,D 是BC 的中点，D E ⊥AB 于E ，DF ⊥AC 于F ，求证：AD 平分∠BACCFABC10.如图BE⊥AC于E，CF⊥AB于F，BE,CF相交于点D，且CE=BF，求证:点D在∠BAC的平分线上11，在Rt△ABC中，∠C=90。

，AC=BC，AD为∠BAC的平分线，AE=BC，DE⊥AB，垂足为E，求证△DBE的周长等于AB.12，在△ABC中，外角∠CBE和∠BCG的平分线相交于点F，求证：点F在∠BAC的平分线上13，已知∠B=∠C=90。

，DM平分∠ADC，AM平分∠DAB，探究线段BM与CM的关系，说明理由。

一、角的平分线性质定理1.角平分线上的点到这个角的两边的距离相等。

2.到一个角的两边距离相等的点在这个角的平分线上。

3.三角形的三条角平分线交于一点，称作内心。

内心到三角形三边的距离相等；4.三角形一个角的平分线，把对边所分成的两条线段与这个角的两邻边对应成比例。

判定：角的内部到角的两边距离相等的点，都在这个角的平分线上。

二、角平分线画法方法11、以点O为圆心，以任意长为半径画弧，两弧交角AOB两边于点M、N。

2、分别以点M、N为圆心，以大于1/2MN的长度为半径画弧，两弧交于点P。

3、作射线OP。

射线OP即为角平分线。

方法21、在两边OA、OB上分别截取OM、OC和ON、OD，使OM=ON，OC=OD。

2、连接CN与DM，相交于P。

3、作射线OP。

射线OP即为角平分线。

三、角平分线定义1、从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线。

2、三角形的一个角的平分线与这个角的对边相交，连结这个角的顶点和与对边交点的线段叫做三角形的角平分线（也叫三角形的内角平分线）。

三角形的角平分线是一条线段。

由于三角形有三个内角，所以三角形有三条角平分线。

三角形的角平分线交点一定在三角形内部。

三角形三条角平分线的交点叫做三角形的内心。

三角形的内心到三边的距离相等，是该三角形内切圆的圆心。

四、角的平分线的定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

1、角的平分线的定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

五、角平分线的性质：角平分线上的点，到角两边的距离相等定理：角平分线上的任意一点，到角两边的距离相等。

垂直于两边为最短距离。

角平分线能得到相同的两个角。

三角形三条角平分线相交于一点，并且这一点到三边的距离相等。

逆定理：到角两边的距离相等的点在角平分线上。