超级画板《动态几何教程》10问题汇编

一 五角星1. 以原点为圆心画圆O ，作出圆O 与y 轴交点A ；2. 同时选择圆O 与点A ，作圆O 的内接正五边形ABCDE ；3. 连接AC 、AD 、BE ，作出AC 与BE 交点F ，AD 与BE 交点G ；4. 构造多边形AFO 、多边形AOG ，分别填充颜色，5. 以点O 位旋转中心，旋转角度为72度，四次旋转后即可得到五角星；6. 隐藏不必要对象。

二 三角形面积公式1. 用智能画笔画出三角形ABC ，分别作出AB ，AC 的中点D ，E ，连接DE ；2. 过点A 向DE 引垂线AF ，F 为垂足；3. 构造多边形ADF ，多边形AFE ；4. 以点D 为旋转中心，t 为旋转角度，旋转多边形ADF ；以点E 为旋转中心，t为旋转角度，旋转多边形AFE ；5. 插入变量t ，范围为0到180；作出t 的动画，动画类型改为“一次运动”，将参数范围的最小值改为0，最大值改为π，点击确定；6. 启动动画即可得到三角形面积公式的推导过程；7. 隐藏不必要对象。

三 平行四边形面积1. 用智能画笔画出平行四边形ABCD ；2. 取AB 上一点E ，作EF 平行于AC 交CD 与F ；3. 过点F 作AB 的垂线FG ，G 为垂足，过点D 作AB 的垂线DH ，H 为垂足；4. 作出点E 在AB 上的一次运动，隐藏线段AB 、AD 、点A ，构造多边形DHBC,多边形EGF ；5. 启动动画即可得到平行四边形的面积演变过程。

四 周长固定20的长方形面积1. 作出坐标点A （a ，0），x 拖动为a ，坐标点B （0,10-a ）；2. 依次选择点B 、O 、A ，做长方形BOAC ；3. 做出曲线)10(x x y -*=，参数范围为0到a ；4.作出点A 的动画，动画类型为一次运动，参数范围为0到10； 5.构造多边形BOAC ，并测量其面积； 6.作出坐标点D （a ，m000），E （5,25） 7. 在点E 的属性对话框填充选项中勾选填充和动态Alpha ，Alpha 通道表达式为255*sign(a ，5)，8. 点E 的纵坐标即为长方形的最大面积，当面积达到最大时显示点E ，点D 的纵坐标即为当前长方形的面积，启动动画，即可得到周长为20的长方形的最大面积。

培优提能10 立体几何中的动态问题立体几何中的“动态问题”是指空间中的某些点、线、面的位置是不确定的或可变的一类开放性问题,解答此类问题应该动静结合、化动为静,找到相应的几何关系,具体有以下几种解决方法:(1)函数法:某些点、线、面的运动,必然导致某些位置关系或一些变量的变化.变量变化时会引发其他变量的变化,从而建立函数关系,将立体几何问题转化为函数问题来解.(2)解析法:我们常利用空间直角坐标系解决立体几何问题,即实现几何问题代数化.因此利用空间直角坐标系将空间图形中的若干元素坐标化后,借助向量进行运算和分析,是解决这类问题的常用方法. (3)等价转换法:动和静是相对的,在运动变化过程中,要善于寻找或构造与之相关的一些不变因素,将一些变化的点、线、面进行合理转换,实现变量与不变量的结合.培优点1 以静制动(旋转问题、射影问题)典例1 正四面体ABCD的棱长为1,棱AB∥平面α(如图),则四面体上的所有点在平面α内的射影构成的图形面积的取值范围是.解析:去掉与问题无关的面,将四面体看成是以AB为棱的二面角C-AB-D(二面角大小一定),用纸折出这个二面角,不妨将AB置于平面α内,将二面角绕AB 转动一周,观察点C,D 在平面α上的射影,可以发现点C,D 在平面α上的射影始终在AB 的射影的中垂线上.当CD ∥平面α时,四边形ABCD 的面积最大,为12(如图1).当CD ⊥平面α时,四边形ABCD 的面积最小,为√24(如图2),转动过程中C,D 在平面α上的射影从C,D 变化到C ′,D ′(如图3),故图形面积的取值范围是[√24,12]. 答案:[√24,12]在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.触类旁通1 如图,直线l ⊥平面α,垂足为O.正方体ABC D −A 1B 1C 1D 1的棱长为2.点A 是直线l 上的动点,点B 1在平面α内,则点O 到线段CD 1的中点P 的距离的最大值为 .解析:从题图中分化出4个点O,A,B1,P,其中△AOB1为直角三角形,固定A,B1,点P的轨迹是在与AB1垂直的平面上且以AB1的中点Q为圆心的圆,从而OP≤OQ+QP=12AB1+2=√2+2,当且仅当OQ⊥AB1,即点O,Q,P共线时,取到等号,此时直线AB1与平面α成45°角.答案:√2+2培优点2 动点轨迹(长度)问题典例2 在棱长为2√2的正方体ABCD-A1B1C1D1中,E,F分别为棱AB,AD 的中点,P为线段C1D上的动点,则直线A1P与平面D1EF的交点Q的轨迹长度为( )A.2√153B.4√33C.2√133D.4√23解析:如图,连接B1D1,因为E,F 分别为棱AB,AD 的中点,所以B 1D 1∥EF,则B 1,D 1,E,F 四点共面.连接A 1C 1,A 1D,设A 1C 1∩B 1D 1=M,A 1D ∩D 1F=N,连接MN,则点Q 的轨迹为线段MN,易得A 1D=√A 1D 12+DD 12=4,△A 1ND 1∽△DNF,且A 1D 1FD=2,所以A 1N=23A 1D=83.易知A 1C 1=C 1D=A 1D=4,所以∠C 1A 1D=60°,又A 1M=2,所以在△A 1MN 中,由余弦定理可得MN 2=A 1N 2+A 1M 2-2A 1N ·A 1Mcos 60°=529,所以MN=2√133,即点Q 的轨迹长度为2√133.故选C.空间中动点轨迹问题变化并不多,一般此类问题可以从三个角度进行分析处理,一是从曲线定义或函数关系出发给出合理解释;二是平面与平面交线得直线或线段;三是平面和曲面(圆锥,圆柱侧面,球面)交线得圆、圆锥曲线.很少有题目会脱离这三个方向.触类旁通2 (多选题)(2022·湖南郴州高三期末)如图,点P 是棱长为2的正方体ABCD-A 1B 1C 1D 1表面上的一个动点,则( AC )A.当点P 在平面BCC 1B 1上运动时,四棱锥P-AA 1D 1D 的体积不变B.当点P 在线段AC 上运动时,D 1P 与A 1C 1所成角的取值范围是[π6,π2]C.当直线AP 与平面ABCD 所成的角为45°时,点P 的轨迹长度为π+4√2D.若F 是A 1B 1的中点,当P 在底面ABCD 上运动,且满足PF ∥平面B 1CD 1时,PF 长度的最小值是 √5解析:当P 在平面BCC 1B 1上运动时,点P 到平面AA 1D 1D 的距离不变,正方形AA 1D 1D 的面积不变,故四棱锥P-AA 1D 1D 的体积不变,故A 正确; 建立如图所示的空间直角坐标系,设P(x,2-x,0),0≤x ≤2,A 1(2,0,2),D 1(0,0,2),C 1(0,2,2),则D 1P →=(x,2-x,-2),A 1C 1→=(-2,2,0),设D 1P 与A 1C 1所成的角为θ(0≤θ≤π2),则cos θ=|cos<D 1P →,A 1C 1→>|=|D 1P →·A 1C 1→||D 1P →||A 1C 1→|=|x -1|√(x -1)2+3,因为0≤|x-1|≤1,当|x-1|=0时,θ=π2,当0<|x-1|≤1时,cos θ=|x -1|√(x -1)2+3=√1+3|x -1|2,0<cos θ≤12,则π3≤θ<π2,综上,π3≤θ≤π2,所以D 1P 与A 1C 1所成角的取值范围是[π3,π2],故B 错误;因为直线AP 与平面ABCD 所成的角为45°,若点P 在平面BCC 1B 1和平面DCC 1D 1内,因为∠B 1AB=45°,∠D 1AD=45°已为最大,不成立,在平面ADD 1A 1内,点P 的轨迹长度是AD 1=2√2,在平面ABB 1A 1内,点P 的轨迹长度是AB 1=2√2, 在平面A 1B 1C 1D 1内,如图所示,作PM ⊥平面ABCD,因为∠PAM=45°,所以PM=AM,又PM=AB,所以AM=AB,则A 1P=AB,所以点P 的轨迹是以A 1为圆心,以2为半径的四分之一圆,所以点P 的轨迹长度为14×2π×2=π,所以点P 的轨迹总长度为π+4√2,故C 正确; 建立如图所示的空间直角坐标系,设P(x,y,0),x,y ∈[0,2],B 1(2,2,2),D 1(0,0,2),C(0,2,0),F(2,1,2),则CB 1→=(2,0,2),CD 1→=(0,-2,2),FP →=(x-2,y-1,-2), 设平面B 1CD 1的法向量为n=(a,b,c),则{CD 1→·n =0,CB 1→·n =0,即{-2b +2c =0,2a +2c =0,令a=1,则n=(1,-1,-1), 因为PF ∥平面B 1CD 1,所以FP →·n=(x-2)-(y-1)+2=0,即y=x+1,所以|FP →|=√(x -2)2+(y -1)2+4=√2x 2-4x +8=√2(x -1)2+6≥√6,当x=1时,等号成立,故D 错误.故选AC.培优点3 翻折问题典例3 如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC 的中心为O.D,E,F 为圆O 上的点,△DBC,△ECA,△FAB 分别是以BC,CA,AB 为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB 为折痕折起△DBC,△ECA,△FAB,使得D,E,F 重合,得到三棱锥.当△ABC 的边长变化时,所得三棱锥体积的最大值为 cm 3.解析:如图,连接OD,交BC于点G,由题意,知OD⊥BC,OG=√3BC.6设OG=x,则BC=2√3x,DG=5-x,×2√3x×3x=3√3x2,三棱锥的高h=√DG2-OG2=√25-10x,S△ABC=12则三棱锥的体积V=1S△ABC·h=√3x2·√25-10x=√3·√25x4-10x5.3),则f′(x)=100x3-50x4.令f′(x)=0,得令f(x)=25x4-10x5,x∈(0,52x=2.当x∈(0,2)时,f′(x)>0,f(x)单调递增;当x∈(2,5)时,f′2(x)<0,f(x)单调递减.故当x=2时,f(x)取得最大值80,则V≤√3×√80=4√15.所以三棱锥体积的最大值为4√15 cm3.答案:4√15在解决立体几何中的“动态”问题时,对于一些很难把握运动模型(规律)的求值问题,可以通过构建某个变量的函数,以数解形.触类旁通3 (1)(多选题)(2022·河北唐山高三期末)如图,四边形ABCD是边长为2的正方形,E为AB的中点,将△AED沿DE所在的直线翻折,使A与A′重合,得到四棱锥A′-BCDE,则在翻折的过程中( AB )A.DE⊥AA′B.存在某个位置,使得A′E⊥CDC.存在某个位置,使得A′B∥DED.存在某个位置,使四棱锥A′-BCDE的体积为1(2)(多选题)(2022·广东罗湖高三期末)在△ABC中,AB⊥BC,且AC=2,BC=1,若将△ABC沿AC边上的中线BD折起,使得平面ABD⊥平面BCD.点E在由此得到的四面体ABCD的棱AC上运动,则下列结论正确的为( BCD )A.∠ADC=π2B.四面体ABCD的体积为18C.存在点E使得△BDE的面积为14D.四面体ABCD外接球的表面积为13π3解析:(1)对于A,如图所示,过A′作A′O⊥DE,垂足为O,延长AO交BC于点F,因为DE⊥AO,且AO∩A′O=O,AO,A′O⊂平面A′AO,所以DE⊥平面A′AO,又因为A′A⊂平面A′AO,所以DE⊥AA′,A正确;对于B,取DC的中点G,连接EG,A′G,当A′在平面ABCD上的射影在直线EG上时,此时DC⊥平面A′EG,从而得到A′E⊥CD,B正确;对于C,连接A′B,因为点E∈平面A′BE,点D∉平面A′BE,所以直线A′B与DE是异面直线,所以不存在某个位置,使得A′B∥DE,C错误;对于D,由VA′BCDE =13×12×(1+2)×2×h=1,解得h=1,由A′O⊥DE,可得A′O=A′E·A′DDE =√5=√5,即此时四棱锥的高h∈(0,√5],此时√5<1,所以不存在某个位置,使四棱锥A′-BCDE的体积为1,D错误.故选AB.(2)对于A,取BD的中点M,连接CM,因为BC=CD=1,所以CM⊥BD,又平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,所以CM⊥平面ABD,则CM⊥AD,若∠ADC=π2,则AD⊥CD,所以AD⊥平面CBD,则AD⊥BD,显然不可能,A错误;对于B,易知△BCD的面积为√34,在平面ABD中,过A作BD的垂线,交BD的延长线于点H,易知AH=√32,因为平面ABD ⊥平面BCD,平面ABD ∩平面BCD=BD,所以AH ⊥平面BCD,即三棱锥A-BCD 的高为AH=√32,所以三棱锥A-BCD 的体积V=13×√34×√32=18,即四面体ABCD 的体积为18,B正确;对于C,显然当AC ⊥平面BDE 时,△BDE 的面积取得最小值,易知CD=1,DH=12,由余弦定理可得CH=√72,所以AC=√AH 2+CH 2=√102, 又四面体ABCD 的体积为18, 所以18=13×S ×√102,即S=3√1040<14, 且△BCD 的面积为√34>14,所以存在点E 使得△BDE 的面积为14,C 正确;对于D,设△BCD 与△ABD 的外心依次为O 1,O 2, 过O 1作平面BCD 的垂线l 1,过O 2作平面ABD 的垂线l 2,则四面体ABCD 的外接球球心O 为直线l 1与l 2的交点,延长CO 1交BD 于点M,则M 为BD 的中点,连接O 2M,则四边形MO 1OO 2为矩形,结合正弦定理可求得O 2M=√32,O 1C=√33, 所以四面体ABCD 的外接球半径为R=OC=√O 1O 2+O 1C 2=√O 2M 2+O 1C 2=√34+13=√1312,则四面体ABCD 外接球的表面积为S=4πR 2=4π×1312=13π3,D 正确.故选BCD.培优点4 动态最值问题典例4 (多选题)(2022·江苏常州高三期末)已知正方体ABCD-A 1B 1C 1D 1的棱长为3a,点M 是棱BC 上的定点,且BM=2CM,点P 是棱C 1D 1上的动点,则( )A.当PC 1=23a 时,△PAM 是直角三角形B.四棱锥A 1-PAM 体积的最小值为32a 3 C.存在点P,使得直线BD 1⊥平面PAM D.任意点P,都有直线BB 1∥平面PAM 解析:由已知及计算可得PC 1=23a,AM=√13a,AP=√2113a,MP=√943a,所以AP 2=MP 2+AM 2,所以△PAM 为直角三角形,A 正确;S △AA 1M =12×3a ×√13a=3√132a 2,当P 与C 1重合时,点P 到平面AA 1M 的距离最小,设点P 到平面AA 1M 的距离为h, 在B 1C 1上取M 1,使B 1M 1=2C 1M 1,sin ∠B 1M 1A 1=√13=ℎmin a,所以h min =√13a,所以V A 1PAM =V PAA 1M =13×S △AA 1M ×h ≥13×3√132a 2×√13a=32a 3,B 正确;因为BD 1⊥平面AB 1C,平面AB 1C 与平面PAM 不平行,所以BD 1与平面PAM 不垂直,C 错误;P 与C 1重合时,平面PAM 为平面C 1AM,BB 1∥CC 1,若BB 1∥平面PAM,则CC 1⊂平面C 1AM,与CC 1⊄平面C 1AM 矛盾,D 错误.故选AB.解决与空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:(1)从问题的几何特征入手,充分利用其几何性质去解决; (2)利用空间几何体的侧面展开图;(3)找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及导数法等.触类旁通4 (多选题)(2022·广东揭阳高三期末)如图所示,已知正方体ABCD-A 1B 1C 1D 1的棱长为2,M,N 分别是AD,CC 1的中点,P 是线段AB 上的动点,则下列说法正确的是( BD )A.平面PMN 截正方体所得的截面可以是四边形、五边形或六边形B.当点P 与A,B 两点不重合时,平面PMN 截正方体所得的截面是五边形C.△MPN 是锐角三角形D.△MPN 面积的最大值是√212解析:如图所示,当点P 与A,B 两点不重合时,将线段MP 向两端延长,分别交CD,CB 的延长线于点O,Q,连接NO,NQ 分别交DD 1,BB 1于R,S 两点,连接RM,SP,此时截面为五边形MPSNR,故B 正确;当点P 与点A 或点B 重合时,截面为四边形,不可能为六边形,故A 错误;考虑△MPN,当点P 与点A 重合时,MN=√6,PM=1,PN=3, 此时因为MN 2+PM 2<PN 2,故∠PMN 为钝角,故C 错误;当点P 与点B 重合时,点P 到直线MN 的距离取到最大值,△MPN 的面积取到最大值,此时MN=√6,BM=BN=√5,则MN 边上的高为√(√5)2-(√62)2=√142,△MPN的面积为12×√142×√6=√212,即最大值为√212,故D正确.故选BD.。

超级画板动态几何的启发作者：安德生来源：《中国信息技术教育》2008年第11期如图1，在平面直角坐标系中，点A、B的坐标分别是（0，5）和（8，0）。

连结AB，得Rt△OAB。

在OB上取一点P（动点），四边形OPMN是Rt△OAB的内接矩形，求矩形面积y与OP长度x之间的函数关系式；并求矩形面积的最大值。

根据图示，由平行线的比例关系，学生不难解答出函数关系式是： y=-—x2+5x，并求出函数最大值为：当x=4时，ymax=10。

但接下来有同学提出这一问题：以点P为顶点的矩形不一定如图示位置，如果过点P作平行于AB且与y轴相交的平行线，然后过点P与这一交点向AB作垂线段，也可以作出内接矩形。

这时会是什么样的呢？这一问题立即引起全班学生的注意，也引起了笔者的兴趣。

于是，笔者决定用超级画板来制作这一新的情况。

课件制作完毕后，笔者和同学们发现一个新大陆：这两个矩形的面积从直觉上看似乎是一样的。

于是我动用测量菜单测量了这两个矩形的面积，结果引起一片哗然：这两个矩形的面积在点P移动过程中竟然保持一致。

于是同学们很容易猜想到：这两种情境下的函数关系式应该是一样的。

有同学通过数学推理计算出第二种情况下的关系式同样是y=-—x2+5x，但是计算过程复杂。

但是笔者想，既然它们的面积是一样的，那么是否可以通过几何法来先证明这两个矩形的面积相等，从而不通过计算得出第二种情况下的函数关系式呢？笔者把这个问题交给学生来思考。

很快，学生通过添加辅助线，验证了这一结论，辅助线添加如图2所示。

如图2，两矩形中△PCM重合，△PCE≌△GAF，△PQM≌△PCM≌△CMN。

因此，欲证两矩形面积相等，需证S矩形OQMD＝S平行四边形GMNA，即OQ×OD=GM×GF（OD=PC=GA）＜＝DM×AG＝GM×GF＜＝△DMG∽△FGA，得证。

对于这一发现，要归功于超级画板对动态作图以及动态中保持数学关系的支持。

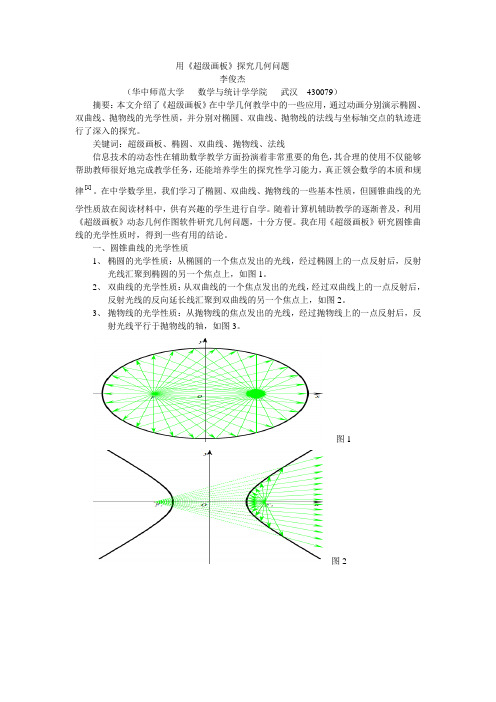
用《超级画板》探究几何问题李俊杰（华中师范大学数学与统计学学院武汉430079）摘要：本文介绍了《超级画板》在中学几何教学中的一些应用，通过动画分别演示椭圆、双曲线、抛物线的光学性质，并分别对椭圆、双曲线、抛物线的法线与坐标轴交点的轨迹进行了深入的探究。

关键词：超级画板、椭圆、双曲线、抛物线、法线信息技术的动态性在辅助数学教学方面扮演着非常重要的角色，其合理的使用不仅能够帮助教师很好地完成教学任务，还能培养学生的探究性学习能力，真正领会数学的本质和规律]1[。

在中学数学里，我们学习了椭圆、双曲线、抛物线的一些基本性质，但圆锥曲线的光学性质放在阅读材料中，供有兴趣的学生进行自学。

随着计算机辅助教学的逐渐普及，利用《超级画板》动态几何作图软件研究几何问题，十分方便。

我在用《超级画板》研究圆锥曲线的光学性质时，得到一些有用的结论。

一、圆锥曲线的光学性质1、椭圆的光学性质：从椭圆的一个焦点发出的光线，经过椭圆上的一点反射后，反射光线汇聚到椭圆的另一个焦点上，如图1。

2、双曲线的光学性质：从双曲线的一个焦点发出的光线，经过双曲线上的一点反射后，反射光线的反向延长线汇聚到双曲线的另一个焦点上，如图2。

3、抛物线的光学性质：从抛物线的焦点发出的光线，经过抛物线上的一点反射后，反射光线平行于抛物线的轴，如图3。

图1图2图3二、用《超级画板》探究法线与坐标轴交点的轨迹 【探究1】：椭圆的法线与坐标轴交点的轨迹先对一个特殊的椭圆1121622=+yx进行研究，用《超级画板》制作如图4所示的动画：点A 为椭圆上任意一点，F 1、F 2为椭圆的焦点，绿色的直线为椭圆在点A 处的法线，法线与x 轴的交点为B,制作点A 的动画，A 为主动点，B 为从动点，对B 进行跟踪，并对B F 2的长度进行测量。

法线是12F AF ∠的角平分线，点B 的轨迹会是怎样的呢？对于这样一个看似简单的问题，起初我们的直觉很可能是点B 在两焦点之间运动，点B 可以跑到线段12F F 上的任意位置，但结果不是这样的。

第二篇平面几何平面几何作为一门系统的学科, 已有两千多年的历史, 其魅力经久不衰。

计算机科技的发展, 推出了动态几何作图软件, 使这门古老的科学焕发青春, 变得更加丰富多彩, 更有吸引力和挑战性。

《超级画板》是由动态几何作图软件发展而来, 平面几何动态作图当然是它的基本功能。

基本功能熟练了, 就有了登堂入室的基础。

这一篇里, 我们将通过一些实例, 学习动态几何作图, 图形的旋转、平移和缩放的操作机制, 图形的测量以及制作控制图形运动和变化的按钮方法。

看了这些例子你会看到, 优秀的作品源于对知识的创造性地运用。

再好的软件也不过是你手中的工具, 不过是圆规直尺铅笔这些古老的工具的发展。

创意永远是最重要的。

首先我们来看看动态几何作图与平时我们在纸上、黑板上作图有什么区别。

（一）共点的三个圆大家一起来试一试, 画出过同一点的三个圆。

合上书本, 自己动手。

完成后, 看看你的制作结果是不是与图中的图形相似？有三个圆, 六个点。

请大家随意拉动几个点试试, 看这三个圆是否还能“过同一点”？拖动结果可能如图2-1所示：图2-1为什么图形会“散架”, 可能作图过程是这样的（图5-2列出了最典型的初学者“画共点的三个圆”的步骤, 受到了传统作图方式如黑板上的绘图或一般绘图软件的影响）。

图2-2在拖动过程中, 动态几何作图能够保持所有给定的几何关系, 因为它就是根据几何关系来设计的！那么, 你思考一下, 上述方法在画圆时, 到底给定了什么样的几何关系？我们知道, 圆是由两个点来决定的, 双击鼠标按下去的点即为圆心, 松开鼠标的点即为圆上的一点。

改变这两个点中的任意一点都可以改变圆。

而在我们刚才的操作中, 我们所给的几何关系是：每个圆都是由两个完全自由的点来决定的（请大家观察一下, 图中共三个圆, 六个自由点）。

根据这样的几何关系, 每个圆都可以随意地改变。

这就表明：在超级画板中, 不能再象在黑板上那样, 随手画出图来, 而每时每刻都得考虑几何关系。

超级几何画板动态作图教程是几何，那就少不了图形，不然何以体现其意，因此作图就是随之而来的非常重要的一方面了，然而通常我们所作的图都是静态的，很多时候不足以令我们满意，那么动态作图怎么说都将是你的“肱股”。

动态作图是本智能软件的重要功能之一，也是本软件的“精彩”之处，当然这个“精彩”是建立在你灵活使用的基础上。

灵活运用动态作图的有关操作以及这些操作的有效组合不但可以按要求准确地画出几何图形，而且具有动态显示功能。

用鼠标拖动点可以改变图形的位置和形状，同时保持几何对象间的几何关系不变（简单地说这就是动态的含义）。

这样可以形象的反映出点与点、点与线、点与面、线与线、线与面以及面与面之间的关系。

借此可以观察出一些重要的几何原理。

在叙述动态作图之前，我们有必要先了解一些基本操作（当然如果你不想的话可以跳过，不过最好是循序渐进，算是“先走后跑”吧）：点的选取：单击“对象选取工具”使其处于被选中状态，然后单击要选取的点。

直线的选取：在“对象选取工具”处于被选中状态时单击要选取的直线，当然你也可以按下Ctrl键，然后依次选取确定直线的两个点来代替选中直线。

平面的选取：在“对象选取工具”处于被选中状态时，依次选中确定平面的三个点多个对象的选取：有时需要将一个以上的几何元素同时处于选中状态，其实现操作是：依次选取所要求的对象；另外的一个方法就是在工作区中连续的选取（单击对象名），同样可以同时选取多个对象，而不需要按下Ctrl键，当然需要记住的是连续选取，不要把鼠标点到作图区中去了；或者使用连选功能。

对象选取中的其他问题：相同对象（例如同是三个点）的选取先后次序不同其实现的意义也往往不同；当误选中某对象时（例如当你选取点B时却不小心误选了点A），你可以再次选取该对象（比如这里的点A），消除其选中状态，然后继续后面的步骤，当然也可以放开Ctrl键消除所有选取动作，再重新选取。

关于作图中的逻辑顺序点：一般在我们作图过程中作点、画线会有先后顺序，点的命名也有一般规则：点的名字按照作点的顺序依次获得在字母表中的字母……，同样，本软件在作图过程中亦是严格遵守此项规则。

动态几何问题的解题技巧解这类问题的基本策略是：1．动中觅静：这里的“静”就是问题中的不变量、不变关系．．．．．．．．，动中觅静就是在运动变化中探索问题中的不变性．．．．2．动静互化：“静”只是“动”的瞬间，是运动的一种特殊形式，动静互化就是抓住“静”的瞬间，使一般情形转化为特殊问题．．．．．．．．．．．，从而找到“动”与“静”的关系．3．以动制动：以动制动就是建立图形中两个变量的函数关系．．．．．．．．．，通过研究运动函数，用联系发展的观点来研究变动元素的关系．总之，解决动态几何问题的关键是要善于运用运动与变化的眼光去观察和研究图形，把握图形运动与变化的全过程，抓住变化中的不变，以不变应万变．．．．．．．．．．．．．。

这类问题与函数相结合时，注意使用分类讨论的思想，运用方程的思想、数形结合思想、转化的思想等。

1、在△ABC中，∠C=90°，AC=BC=2，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC、CB与点D、点E，图①，②，③是旋转得到的三种图形。

（1）观察线段PD和PE之间的有怎样的大小关系，并以图②为例，加以说明；（2）△PBE是否构成等腰三角形？若能，指出所有的情况（即求出△PBE为等腰三角形时CE的长，直接写出结果）；若不能请说明理由。

2、如图，等腰Rt△ABC(∠ACB＝90°)的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，(1)求y 与x 之间的函数关系式；(2)当△ABC 与正方形DEFG 重合部分的面积为32时，求CD 的长． 3、在平面直角坐标系中，直线1l 过点A(2，0)且与轴y 平行，直线2l 过点B(0，1)且与轴x 平行，直线1l 与2l 相交于点P 。

动态几何_广州大学中国大学mooc课后章节答案期末考试题库2023年1.用菜单作变量尺，如果作4个，要操作（）次。

答案:42.要作两个点的定比分点，在方便面中用（）命令。

答案:dbfd3.井田问题中，中间一块小四边形形的面积是整个大四边形面积的（）答案:1/44.函数y=a*sin(b*x+c)中的c表示（）答案:周期5.下面哪一个是直线的截距式方程？答案:x/a+y/b=16.空间坐标系中，哪一个卦限的坐标全为负值？答案:77.超级画板中，下列哪个对象不能被跟踪？答案:文本8.在对象列表中选定跟踪对象后，怎样打开它的属性对话框？答案:单击鼠标右键9.2的128次方的最后一位数字是（）答案:610.在程序区输入：Complex(1);(3+2*i)*(1+i);运行后得到的结果是（）答案:1 + 5*i11.在超级画板中，对圆可以测量它的（）。

答案:周长半径面积12.超级画板其课件演示的特点是（）答案:大屏幕、全屏幕加按钮、设窗口多文档、多页面可预设、可实时13.方便面命令的构成规律主要有（）。

答案:考虑到三个字母有重码可能，对个别函数的命名不是完全按照以上两条原则，如为了区分“圆锥焦点yzjd(C)”和“圆锥顶点yzdd(C)”，就采用了4个字母。

汉字命令不超过3个字时，取拼音的第一个字母组成英文命令。

例如：函数表就是hsb,旋转就是xz,平移就是py。

与测量有关的函数命令，前面统一加c代表测量的意思。

汉字命令长度超过3个字时，取前面2个字和最后一个字的拼音的第一个字母组成英文命令。

例如：函数曲线就是hsx, 极坐标曲线就是jzx, 圆内接正n边形就是ynx。

14.超级画板中，调节参数的方式有（）答案:作包含参数的坐标点,设置好拖动参数作参数的动画作参数的变量尺15.空间到平面平行投影画法的关键是（）答案:平行的线段的比不变平行关系不变共线关系不变16.下列属于时序动画的是（）答案:Flash动画动画片电影17.逻辑动画的特点有（）答案:占用的空间少制作过程简单适合用于说明事物变化规律能够较准确地表达数量位置逻辑关系18.动画运动的类型有（）答案:重复运动一次运动往返运动19.超级画板中，符号函数sign(a,b)返回的值可能是（）答案:120.动态几何中可以动态实现以下哪些功能？答案:写、画推、算测、变编、演21.超级画板的方便面是方便的空白页面的简称。

利用几何画板解决动态几何问题本文从三个方面谈谈动态几何问题的解题思路.一、动点问题动点问题是探索某个儿何图形上，一个或儿个点在运动变化过程中形成的数量关系、图形状态、图形之间的特殊关系等.解决此类问题，须关注点的运动方向、范围和速度，以便确定是否需要分类讨论.例1 已知直角坐标系中，菱形ABCD的位置如图1, C、D两点的坐标分别为(4,0), (0, 3),线段BE是菱形的高.现在有两个动点P, Q分别从A, C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.(1)求菱形ABCD的边长和它的而积及BE的长；(2)探究下列问题：①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA 上时，求AAPQ的面积S关于t的函数关系式，以及S的最大值；②若点P的速度为每秒1个单位，点Q的速度为每秒k个单位.在运动过程中，任何时刻都有相应的聶值，使得AAPQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形.探究(=4秒的情形，并求出k的值.解析问题(1)比较简单，利用勾股定理就能求出菱形的边长和面积及BE的长；问题(2)的第①小题中，由于点P、Q都在运动，AAQP的大小在变化，点P、Q的运动吋间范围都不知道，因此求AAQP的血积的函数关系式及血积的最大值感觉无从下手，那么，如何才能解决问题呢？利用儿何画板作图1观察：①点击鼠标使点P、Q同时运动，观察点P、Q停止运动的时刻，找出运动时间范围；②观察AAQP大小随时间变化而变化，并在不同时刻作出它的高，找出AAQP的面积最大时刻；③观察这些三角形的高有什么位置关系？它们与线段BE有什么关系？④利用三角形相似，可以求出厶AQP的高.这样，它的面积为：242 24- ------- 1 + —t25 524/= -25('-y) +&0 < t < 5,・•・当“•时,S = 6.问题(2)的第②小题中，由于等腰三角形AQP并没有指定它的两腰，所以结论必须分情况讨论.利用几何画板作图2观察：点击鼠标使点P、Q同时运动，观察点Q的位置随着时间变化而变化，当点Q分别在边AB或边BC±时，来讨论AQAP三边之间的关系.图2（i ） 当点Q 在边BC 上时,PQNBE>PA, 只存在点Q,使QA = QP.•・• ACQM s MFM,・些二坐co _丝…CQ _ AF 1 V — 5，妣 22 i 114k = = 10；（ii ） 当点Q 在AB 上时，存在两点分别使 AP = AQ.AP = PQ.若AP = AQ （如图3）,则必=10 - 4 = 6,jt = y;若PA = PQ （如图4）,通过点P 作PF 丄 AQ,垂足为F ・由空—陛田 AP 一 AS'综合上所述，当t=4秒，以所得的等腰三角形APQ 沿底边翻折，翻折后得到菱形的k 值为耳，或丄，或2Z.10 2 50点评此题是以点的运动为背景，难度较大的一道综合题.抓住动点Q 与定点A,与得P ，譽二% AF = - P 尸25 9偿） AQ = 2AF = g. 于是，必=10 -誇 19425，97502825 9P构成等腰三角形是关键，再分类讨论，综合分析得出结论.二、动线问题动线问题是探索某个几何图形上，某线段在运动变化过程中形成的数量关系、图形的状态、图形之间的特殊关系等.例2 已知如图5,等边三角形ABC的边长为4厘米，长为1厘米的线段““在厶ABC的边上沿AB方向以1厘米/秒的速度向B点运动(运动开始时，点M与点A重合, 点IV到达B 点时运动终止).过点M、N分别作AB的垂线，与AABC的其它边交于P、Q两点，线段MN 运动的时间为t秒.(1)线段MN在运动的过程中，t为何值时，四边形MNQP恰为矩形？并求出该矩形的面积;(2)线段MN在运动的过程中，四边形MNQP的面积为S,运动的时间为t,求四边形MNQP的面积S随运动时间t的变化的函数关系式，并写出自变量t的取值.图5 图6解析在题(1)中，可利用几何画板作图6,点击鼠标使线段MN运动，观察四边形MPQN 的形状，当四边形MPQN为矩形时使运动停止，分析可知此时AACB的高是线段MN的垂直平分线，问题也就迎刃而解了.题(2)中的关键问题是，随着时间变化，四边形MPQN不但形状变化而旦大小也在变化.对此，可利用儿何画板作图7、图8、图9,用鼠标点击，使线段肘IV运动，观察四边形MPQN 的形状可以知道，在不同的时间段，四边形MPQN的形状大小都在变化，须分别讨论.⑴线段MN在点D的左侧，四边形MNQP是梯形，如图7. t的取值范围是OWtWl.(ii) 线段MN 在D 点的两侧，四边形MNQP 是梯形，如图8. t 的取值范围是 lWtv2・ (iii) 线段MN 在点D 的右侧，四边形MNQP 是梯形，如图9. t 的取值范圉是253.四边形PMNQ 的面积点评 线段MN 在AB 上运动，本质是相距1厘米的两动点M 、N 在线段AB 上运动, 将线段化为两端点的运动，抓住动点或动线的特点与规律，注意变化中图形的性质和特征, 进而求解.三、动面问题动面问题是探索在某个几何图形上，面在运动变化过程中形成的数量关系、图形的特 殊状态、图形Z 间的特殊关系等.A MN DB 图7A M "幵B 图8 • A D M N B图9-^31 + •事(2 < t < 3).2例3 如图10,在AABC 屮，ZC=45° , BC=10，高AD = 8.矩形EFPQ 的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H.(1)求证:(2)设EF=x,当x为何值时，矩形EFPQ的面积最大？并求其最大值;(3)当矩形EFPQ的而积最人时，该矩形EFPQ以每秒1个单位的速度沿着射线QC匀速运动(当点Q与点G重合时停止运动).设运动时间为t秒，矩形EFPQ与AABC重壳部分的面积为S,求S与t的两数关系式.图10解析问题⑴⑵根据三角形相似就能解决；对问题(3),难度在于矩形QEFP随着时间的变化与AABC重叠部分的形状不断变化, 可利用几何画板作图，点击鼠标使矩形QEFP运动，观察可以知道在不同的时间段，矩形QEFP与AABC重叠部分的形状大小都在变化，须分吋间段讨论.(i)当0Wl<4时，矩形与ZXABC重程的部分为五边形EQ】PNM(如图11)；(ii)当4^1<5时，矩形与AABC重輕部分而积为直角梯形(如图12)；(iii)当5WtW9时，矩形与AABC重叠部分面积是等腰直角三角形(如图13).A图13则S与t的函数关系式为:-斗2 +20(0 W £ < 4),S =--4r +28(4 w t < 5),*(9 7)2(5 WtW9)・・点评本题第(3)问的难点是：由t的变化，矩形EFPQ被线段AB所截与AABC重叠部分将依次为五边形、四边形、三角形，最后消失.它蕴含着分类讨论的思想方法，须先确定t 的变化范围，再求面积S.。