当前位置：文档之家 › 四探针法测电阻率实验原理

四探针法测电阻率实验原理

  • 格式：docx
  • 大小：140.80 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

【优秀资料】四探针方法测电阻率原理公式推导PPT

【优秀资料】四探针方法测电阻率原理公式推导PPT

（a）块状和棒状样品体电阻率测量： 由于块状和棒状样品外形尺寸与探针间距 比较，合乎于半无限大的边界条件，电阻 率值可以直接由（１）、（２）式求出。
（b）簿片电阻率测量 簿片样品因为其厚度与探针间距比较， 不能忽略，测量时要提供样品的厚度形 状和测量位置的修正系数。
电阻率值可由下面公式得出：
C V IG (W S)D (d S)0G (W S)D (d S)
• 测量电阻时，可以按表所示的电压电流量程进 行选择。
电流 / 电阻 / 电压 0.2mV 2mV
20mV
200m V
在半导体材料断面测量时：直径范围 Φ15~100mm，其高度为400mm，如果要对大 于400mm长单晶的断面测量，可以将座体的 V型槽有机玻璃板取下，座体设有一个腰形 孔，用户可以根据需要增设支衬垫块使晶体 长度向台下延伸，以满足测量长单晶需求， 测试架有专门的屏蔽导线插头与电气箱联结。
<四> 实验步骤
式中：ρ0 为块状体电阻率测量值； W：为样品厚度（um）；S：探针间距（mm）； G(W/S)为样品厚度修正函数，可由附录IA或附录 1B查得； D(d/S)为样品形状和测量位置的修正函数，可由附 录２查得。W/S＜0.5时，实用。 当圆形硅片的厚度满足W/S＜0.5时，电阻率为：
0W S2l1n2D(dS)
R ( )4.53 S：探针间距（mm）；
0
ln2 I I 5、仪器在中断测量时应将工作选择开关置于“短路”；
当半导体薄层尺寸满足于半无限大时：
3、方块电阻测量，电流调节在4.
2、打开电源并预热１小时。
S：探针间距（mm）；
3、方块电阻测量，电流调节在4.
若取I ＝ 4.53 I ，I 为该电流量程满度值， 当半导体薄层尺寸满足于半无限大时：

四探针方法测电阻率 原理公式推导

四探针方法测电阻率 原理公式推导
式中：ρ0 为块状体电阻率测量值； W：为样品厚度（um）；S：探针间距（mm）； G(W/S)为样品厚度修正函数，可由附录IA或附录 1B查得； D(d/S)为样品形状和测量位置的修正函数，可由附 录２查得。W/S＜0.5时，实用。 当圆形硅片的厚度满足W/S＜0.5时，电阻率为：
0W S2l1n2D(dS)
探针方法测量半导体的电阻率
〈一〉实验目的 〈二〉实验原理 〈三〉仪器结构特征 〈四〉操作步骤 〈五〉注意事项 〈六〉技术参数
<一> 实验目的
1、理解四探针方法测量半导体电阻率的原理； 2、学会用四探针方法测量半导体电阻率。
<二> 实验原理
1、体电阻率测量：
当１、２、３、４四根 金属探针排成一直线时， 并以一定压力压在半导体 材料上，在１、４两处探 针间通过电流I，则２、３ 探针间产生电位差V。
四探针法测量原理图Βιβλιοθήκη 材料电阻率 VC(1)
I
探针系数
C 11
20π 1
1
(2)
S1 S2 S1S2 S2S3
式中：S1、S2、S3分别为探针１与２，２与３，３ 与４之间距，用cm为单位时的值，S1=S2=S3=1mm. 每个探头都有自己的系数。C6.280.05单位cm。
若电流取I = C 时，则ρ＝V，可由数字电压表直 接读出。
4、将工作选择档置于“自校”，使电流显示出 “１９９＊”，各量程数值误差为４字。
5、将工作选择档置于“调节”，电流调节在I ＝6.28=C，C为探针几何修正系数。
1.显示板 2、单位显示灯 3、电流量程开关 4、工作选择开关 （短路、测量、调节、自校选择）5、电压量程开关6、输入插 座7、调零细调8、调零粗调9、电流调节10、电源开关11、电 流选择开关 12、极性开关

四探针法测量电阻率

四探针法测量电阻率
实验二 四探针法测量电阻率
一、引言 电阻率是反映半导体材料导电性能的重要参数之一.虽然测量电阻率的方法很多, 但由于四探针法设备简单、操作方便、精确度高、测量范围广，而且对样品形状无严 格要求，不仅能测量大块材料的电阻率，也能测量异形层、扩散层、离子注入层及外 延层的电阻率，因此在科学研究及实际生产中得到广泛利用。 本实验是用四探针法测量硅单晶材料的电阻率及 pn 结扩散层的方块电阻。通过 实验，掌握四探针法测量电阻率的基本原理和方法以及对具有各种几何形状样品的修 正，并了解影响测量结果的各种因素。 二、原理 1、 四探针法测量单晶材料的电阻率 最常用的四探针法是将四根金属探针的针尖排在同一直线上的直线型四探针法，如 图 2.1 所示。当四根探针同时压在一块相对于探针间距可视为半无穷大的半导体平坦表 面上时，如果探针接触处的材料是均匀的，并可忽略电流在探针处的少子注入，则当电 流 I 由探针流入样品时，可视为点电流源，在半无穷大的均匀样品中所产生的电力线具 有球面对称性，即等势面为一系列以点电流源为中心的半球面。样品中距离点电源 r 处 的电流密度 j，电场ε和电位 V 分别为
0
式中 q 为电子电荷，u 为扩散层中多数载流子的迁移率。因此，可引入扩散层平均电阻 率 ，可以证明，
R X j C 0
三、实验装置
V23 X j ............(15) I
实验装置主要由三部分组成：四探针头、电流调节装置、电压测试仪。 1、 四探针头 四根探针头要等距离地排列在一直线上，探针间距要固定（通常约为 1mm 左右） ， 游移度要小。探针头地曲率半径约为 50um 左右，探针之间的电绝缘性能要好。为了 使探针和样品形成较好的欧姆接触，要求探针与待测材料有较低的接触电势差，而且 探针和样品之间要加一定的压力（每根探针压力为 100－200g） 。因此，探针要用导电 性能好的硬质、耐磨金属制成，通常采用钨、碳化钨、锇铱合金、合金钢等。 2、 电流调节装置 四探针法的测试电路如图 2.2 所示。

四探针法测电阻率共14页

四探针法测电阻率共14页

实验四探针法测电阻率1．实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2．实验内容①硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

②薄层电阻率的测量：对不同尺寸的单面扩散片和双面扩散片的薄层电阻率进行测量。

改变条件进行测量（与①相同），对结果进行比较。

3．实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法，四探针法，单探针扩展电阻法，范德堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

所谓四探针法，就是用针间距约1毫米的四根金属探针同时压在被测样品的平整表面上如图1a所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用高输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算出样品的电阻率［１］式中，C为四探针的修正系数，单位为厘米，C的大小取决于四探针的排列方法和针距，探针的位置和间距确定以后，探针系数C 就是一个常数；V 23为2、3两探针之间的电压，单位为伏特；I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相关，下面我们分两种情况来进行讨论。

⑴ 半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻率的装置；(b)为半无穷大样品上探针电流的分布及等势面图形；(c)和(d)分别为正方形排列及直线排列的四探针图形。

因为四探针对半导体表面的接触均为点接触，所以，对图１（b ）所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位面为图中虚线所示的半球面。

于是，样品电阻率为ρ，半径为r ，间距为dr 的两个半球等位面间的电阻为 它们之间的电位差为 dr r IIdR dV 22πρ==。

四探针法的基本原理

四探针法的基本原理

四探针法的基本原理
四探针法是一种常用的测量电阻的方法，它的基本原理是利用四个电极探针同时接触待测物体的表面，通过测量电流和电压，计算出物体的电阻值。

四探针法主要利用了电流通过导体时会引起电压降的原理。

在该测量方法中，有一个固定电流源，将一定大小的电流通过待测物体的表面，同时四个探针分别接触物体的四个不同位置。

这四个探针中的两个被用作电流引入，另外两个则用于电压测量。

当电流流过物体时，会在物体内产生电流流向相反的电势差，即电压降。

在探针中测量到的电压值，正是由于电流通过导体时所引起的电压降。

通过测量探针之间的电压差和流经物体的电流值，可以利用欧姆定律计算出物体的电阻值。

与其他电阻测量方法相比，四探针法能够有效消除探针和待测物体之间的接触电阻和电流分布的影响，从而提高测量的准确性。

此外，四探针法还能够测量较小尺寸的样品，因为它不需要通过样品中心点进行电流引入。

总之，四探针法是通过测量电压和电流，利用欧姆定律计算出物体的电阻值的一种测量方法，它消除了探针接触电阻和电流分布对测量结果的影响，具有较高的测量精度和适用范围。

四探针法测量材料的电阻率和电导率

四探针法测量材料的电阻率和电导率

实验七：四探针法测量材料的电阻率和电导率ID:20110010020［实验目的］:1、了解四探针电阻率测试仪的基本原理；2、了解的四探针电阻率测试仪组成、原理和使用方法；3、能对给定的物质进行实验，并对实验结果进行分析、处理［实验原理］:单晶硅体电阻率的测量测试原理：直流四探针法测试原理简介如下:当1、2、3、4根金属探针排成直线时，并以一定的压力压在半导体材料上，在1、4两处探针间通过电流I,则2、3探针间产生电位差V。

材料的电阻率尸/Ss）（1>式中C为探针系数，由探针几何位置、样品厚度和尺寸决定，通常表示为C=F（D/S）・F（W/S）,E乎，W⑵式中：F（WS）F（D/S>Fsp分别样品厚度修正因子、直径修正因子、探针间距修正系数（四探针头合格证上的F值）。

W:片厚，D:片径，S:探针间距。

［实验装置］:使用RTS-4型四探针测试仪1、电气部分：过DC-DC变换器将直流电转换成高频电流，由恒流源电路产生的高频稳定恒定直流电流其量程为0.1mA、1mA、10mA、100mA;数值连续可调，输送到1、4探针上，在样品上产生电位差，此直流电压信号由2、3探针输送到电气箱内。

再由高灵敏，高输入阻抗的直流放大器中将直流信号放大（放大量程有0.763、7.63、76.3）。

放大倍数可自动也可人工选择，放大结果通过A/D转换送入计算机显示出来。

RTS-例四探针测试仪框图如下所示。

国2四探」期试M电气刍分原理方也:2。

测试架探头及压力传动机构、样品台构成，见图3所示，探头采用精密加工，内有弹簧加力装置，测试需要对基片厚度进行测量，以便对探头升降高度进行限制。

图3测试架结构图［实验内容］:一、测试准备：将220V电源插入电源插座，开机后等十分钟在进行测量。

1 .利用标样学习测试参数确定：进入系统，打开主界面。

Q选择参数：选择测试类别（如薄圆片还是棒材电阻率等）；酬入参数：片厚（mm）；直径；选择电流量程。

半导体物理实验——四探针法测半导体材料电阻

半导体物理实验——四探针法测半导体材料电阻四探针法的原理是将四个探针分别接触到半导体材料的表面，在一个恒定的电流下测量电压的变化，从而计算出材料的电阻。

与传统的两探针法相比，四探针法排除了接触电阻对电阻测量的干扰，从而得到更为准确的结果。

在进行实验之前，需要准备好以下器材和器件：半导体样品、四探针测试仪、示波器、多用途电源等。

首先，将半导体样品放置在四探针测试台上，保证样品表面平整。

接下来，使用四个探针将样品分别接触，确保四个探针之间的距离尽量相等，并且垂直于样品表面切面。

在接触探针的过程中，需要注意避免对样品造成损伤。

接触完四个探针后，将示波器和多用途电源连接到四探针测试仪上。

示波器用于测量电压的变化，而多用途电源则提供恒定的电流。

通过调节多用途电源的参数，可以使得流过样品的电流保持恒定。

开始实验之前，需要对四探针测试仪进行校准。

校准的目的是消除探针接触电阻的影响，确保测量结果的准确性。

校准时，将四个探针分别接触到一个已知电阻的样品上，通过测量电压和电流的变化来确定校准系数。

校准完成后，开始进行实际的测量。

首先，通过调节多用途电源的参数使得电流稳定在预定的数值。

然后，使用示波器测量电压的变化，并记录下来。

在测量过程中，可以逐渐调节电流的数值，以获得多组测量数据，从而提高测量结果的可靠性。

测量完成后，可以根据测得的电流和电压数据，计算出半导体样品的电阻。

根据四探针法的原理，可以得到以下公式：电阻率ρ = (π/ln2) × (d/U) × (U/I)其中，d是四个探针之间的距离，U是电压的变化值，I是电流的恒定值。

除了电阻率，四探针法还可以用来计算半导体材料的载流子浓度。

载流子浓度是半导体材料性能的重要指标之一，在半导体器件研发和生产过程中有着广泛的应用。

通过四探针法测量半导体材料的电阻，可以得到材料的电学性质信息，为半导体器件的设计和制造提供重要的依据。

实验人员可以根据实验结果，进一步探究半导体材料的物理特性，并优化材料的制备工艺，提高器件的性能。

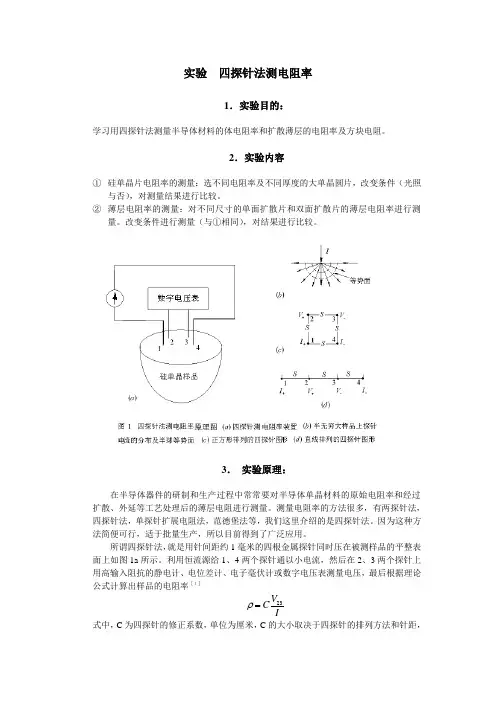
四探针法测电阻率实验原理

实验 四探针法测电阻率1．实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2．实验内容① 硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

② 薄层电阻率的测量：对不同尺寸的单面扩散片和双面扩散片的薄层电阻率进行测量。

改变条件进行测量（与①相同），对结果进行比较。

3． 实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法，四探针法，单探针扩展电阻法，范德堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

所谓四探针法，就是用针间距约1毫米的四根金属探针同时压在被测样品的平整表面上如图1a 所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用高输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算出样品的电阻率［１］IV C23=ρ 式中，C 为四探针的修正系数，单位为厘米，C 的大小取决于四探针的排列方法和针距，探针的位置和间距确定以后，探针系数C 就是一个常数；V 23为2、3两探针之间的电压，单位为伏特；I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相关，下面我们分两种情况来进行讨论。

⑴ 半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻率的装置；(b)为半无穷大样品上探针电流的分布及等势面图形；(c)和(d)分别为正方形排列及直线排列的四探针图形。

因为四探针对半导体表面的接触均为点接触，所以，对图１（b ）所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位面为图中虚线所示的半球面。

于是，样品电阻率为ρ，半径为r ，间距为dr 的两个半球等位面间的电阻为dr r dR 22πρ=， 它们之间的电位差为 dr r IIdR dV 22πρ==。

四探针方法测电阻率(原理公式推导) PPT

4、薄片电阻率测量：当薄片厚度>0.5mm时， 按公式（3）进行；当薄片厚度<0.5mm时， 按公式（4）进行。
5、仪器在中断测量时应将工作选择开关置于 “短路”；电流开关置于弹出断开位置。
电阻率值可由下面公式得出：
C V IG (W S)D (d S)0G (W S)D (d S)
式中：ρ0 为块状体电阻率测量值； W：为样品厚度（um）；S：探针间距（mm）； G(W/S)为样品厚度修正函数，可由附录IA或附录 1B查得； D(d/S)为样品形状和测量位置的修正函数，可由附 录２查得。W/S＜0.5时，实用。 当圆形硅片的厚度满足W/S＜0.5时，电阻率为：
0W S2l1n2D(dS)
2、带扩散层的方块电阻测量 当半导体薄层尺寸满足于半无限大时：
V
V
R0
( )4.53
ln2 I
I
若取I ＝ 4.53 I0，I0为该电流量程满度值， 则R0值可由数字表中直接读出的数乘上10 后得到。
<三> 仪器结构特征
• 数字式四探针测试仪主体部分由高灵敏 度直流数字电压表、恒流源、电源、DCDC电源变换器组成。为了扩大仪器功能 及方便使用，还设立了单位、小数点自 动显示电路、电流调节、自校电路和调 零电路。
• 温度影响电阻率,从面影响电阻
• p=p1(1+aT),p1为该材料0摄氏度时的电阻 率, a叫电阻的温度系数,不同材料的电阻 温度系数不同
• 由R=p*l/s p=p1(1+aT),得
• R=R1(1+aT) 同理,R1为0摄氏度时的电阻
• R=p*l/s(p—电阻率查表求；l—电阻长度 ；s—与电流垂直的电阻截面面
• 为克服测试时探针与样品接触时产生的接触 电势和整流效应的影响。本仪器设立有“粗 调”、“细调”调零电路能产生一个恒定的 电势来补偿附加电势的影响。

四探针法的基本原理

四探针法的基本原理
四探针法是一种在金属材料表面进行电导率测试的方法。

它的基本原理是通过四个电极（即四个探针）同时接触到被测试材料的表面，其中两个电极作为输入端，在它们之间施加一个恒定的电流；另外两个电极作为输出端，测量输入电流通过材料时的电压差。

根据欧姆定律，电导率与电阻之间有一定的关系，电导率越高，电阻越低。

所以通过测量输入电流的电压差，可以计算出材料的电阻。

进而通过该电阻值，就可以推算出材料的电导率。

四探针法的特点是能够消除探针电阻和触点对测量结果的影响，提高测量的精确度。

同时，由于采用了四个探针，可以减小探针导线与被测材料的接触电阻，进一步提高测量的准确性。

总结起来，四探针法的基本原理是通过在被测试材料表面施加一定电流，测量电压差，并根据欧姆定律计算出材料的电阻，从而推算出材料的电导率。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验四探针法测电阻率1.实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2.实验内容①硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

②薄层电阻率的测量：对不同尺寸的单而扩散片和双而扩散片的薄层电阻率进行测量。

改变条件进行测疑（与①相同），对结果进行比较。

1 2 3 4你 E恒）图1四按针法測电磴車煉建图0｝四慄計測倒F且奉装貫Q）半无筲犬祥品上探针帧的分布炭半球等势面k）正方形排列的四探针爲直线枠列的四探针圏形3.实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法, 四探针法，单探针扩展电阻法，范徳堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

所谓四探针法，就是用针间距约1亳米的四根金属探针同时压在被测样品的平整表面上如图la所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用髙输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算岀样品的电阻率m式中，C为四探针的修正系数，单位为厘米，C的大小取决于四探针的排列方法和针距,探针的位巻和间距确泄以后，探针系数C 就是一个常数：V23为2、3两探针之间的电 压，单位为伏特：I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相 关，下面我们分两种情况来进行讨论。

(1)半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻 率的装置：(b)为半无穷大样品上探针电流的分布及等势而图形；(c)和(d)分别为正方形 排列及直线排列的四探针图形。

因为四探针对半导体表而的接触均为点接触，所以，对 图1(b)所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位而为图中虚线所示的半球面。

于是，样品电阻率为P,半 径为r,间距为dr 的两个半球等位而间的电阻为dR = -^dr,它们之间的电位差为dV = IdR = ^dr°2加「考虑样品为半无限大，在r-8处的电位为0,所以图1流经探针4的电流•与流经探针1的电流方向相反，所以流经探针4的电流I 在探针2、于是流经探针1、 4之间的电流在探针2、 3之间形成的电位差为由此可得样品的电阻率为p=^\--丄-丄+丄『(1)/1人2 斤3r42r43 )上式就是四探针法测半无限大样品电阻率的普遍公式。

在采用四探针测量电阻率时通常使用图1(C)的正方形结构(简称方形结构)和 图1 (d)的等间距直线形结构，假设方形四探针和直线四探针的探针间距均为S, 则对于直线四探针有金=知=S,斤厂=r 42=2S⑵对于方形四探针有金=金=S, 6 = 742=^52於 厶(a)中流经探针1的电流I 在r 点形成的电位为讣4歸流经探针1的电流在2、3两探针间形成的电位差为3之间引起的电位差为（2）无限薄层样品情形当样品的横向尺寸无限大，而其厚度t 又比探针间距S 小得多的时候，我们称这种 样品为无限薄层样品。

图2给出了用四探针测量无限薄层样品电阻率的示意图。

图中被 测样品为在p 型半导体衬底上扩散有n 型薄层的无限大硅单晶薄片，1、2、3、4为 四个探针在硅片表面的接触点，探 针间距为S, n 型扩散薄层的厚度为 t.并且t«S, 1+表示电流从探针1 流入硅片，L 表示电流从探针4流岀 硅片。

与半无限大样品不同的是， 这里探针电流在n 型薄层内近似为 平而放射状，其等位而可近似为圆 柱面。

类似前而的分析，对于任意 排列的四探针，探针1的电流I 在 样品中r 处形成的电位为式中P 为n 型薄层的平均电阻率。

于是探针1的电流I 在2.3探针间所引起的电位差为 2刃D2加 公同理, 探针4的电流I 在2、 3探针间所引起的电位差为所以探针1和探针4的电流I 在2、 3探针之间所引起的电位差是于是得到四探针法测无限薄层样品电阻率的普遍公式为对于直线四探针，利用G = ro = S, ^ = ^ = 25可得卩沖2舒对于方形四探针，利用= y]2S 可得（6）在对半导体扩散薄层的实际测量中常常釆用与扩散层杂质总疑有关的方块电阻Rs ，它 与扩散薄层电阻率有如下关系:R s =丄=—— ------ = —1—甸2无限溥层样品电阻率3Xj NdX这里Xj为扩散所形成的pn结的结深。

这样对于无限薄层样品，方块电阻可以表示如下: 直线四探针：壬字（7）S3单面扩敬和双面扩敌的薄层（3）单面扩豹旳薄层・（b）或朗扩散的理层方形四探针: 在实际测量中，被测试的样品往往不满足上述的无限大条件,样品的形状也不一肚相同, 因此常常要引入不同的修正系数。

实际测量中的扩散样片可能有两种情况：单而扩散片和双而扩散片，如图3所示。

这两种样品的修正系数分别列于附录中的表。

图4 SZT-2A四探针测试仪4.实验装置及注意事项（1）实验装置实验装置如图4所示。

电路中的恒流源所提供的电流是连续可调的，电压表采用电位差讣或数字电压表。

实验所用的探针通常釆用耐磨的导电硬质合金材料，如铸、碳化铸等。

探针要求等间距配置，并使其具有很小的游移误差©在探针上需加上适当的压力,以减小探针与半导体材料之间的接触电阻。

⑵注意事项①半无限大样品是指样品厚度及任意一根探针距样品最近边界的距离远大于探针间距，如果这一条件不能得到满足则必需进行修正。

②为了避免探针处的少数载流子注入，提高表而复合速度，待测样品的表而需经粗砂打磨或喷砂处理。

③在测量高阻材料及光敏材料时需在暗室或屏蔽盒内进行。

④因为电场太大会使载流子的迁移率下降，导致电阻率测量值增大，故须在电场强度E<lV/cm的弱场下进行测量。

⑤为了避免大电流下的热效应，测试电流应尽可能低，但须保证电压的测试精度。

不同电阻率样品的电流选择大致为12)⑥为了满足探针与半导体的接触为欧姆接触，探针上须加上一立的压力。

对于体材料，一般取l~2kg：对于薄层材料或外延材料选取200g。

⑦当室温有较大波动时，最好将电阻率折算到23°C时的电阻率。

因为半导体的电阻率对温度很敏感。

如果有必要考虑温度对电阻率的影响，可用下而的公式进行计算。

歩右=Q平均［1 一G (丁一心考)」⑼式中为修正到某一参考温度(例如23°C)下的样品电阻率；P作为测试温度下样品的平均电阻率：G•为温度系数，它随电阻率变化的曲线示于图5；T为测试温度: T冬勺为某一指定的参考温度。

图5 H-Si(a)和P£i(b)的电阻率温度系数随电阻率的变化5.附录附录1A 样品厚度修正系数G （首）w样品厚度较薄：M 二0.001“见表5W ：样品厚度（um ）： S ：探针间距（mm ）0.21210」51 」52」53 .154」54 」55 」56 」57 」57」58W/S W 0 0.00 0 .000 0.01 10 .007 0.02 20 .014 0.03 30 .022 0.04 40 .029 0.05 50 .036 0.06 60 •043 0.07 70 .051 0.08 80 .058 0.09 90 .065 0.10 100 .072 0.11 110 .079 0.12 120 .087 0.13 130 .0940.14 140 」01 0.15 150 」08 0.16 160 」15 0.17 170 」23 0.18 180 」30 0.19 190 」370.20 200 • 1441 2 3 .001 .001 .002 .008 .009 .009 .015 .016 .017 .022 .023 .024 .030 .030 .031 .037 .038 .038 .044 .045 .045 .051 .052 .053 .058 .059 .060 .066 .066 .067 .073 .074 .074 .080 .081 .082 .087 .088 .089 .095.095 .096」02 .102 」03 」09.110 」10 .116.117 」18」23.124.125 .131 」31.132 .138.139 .139」45 .145」464 5 6 .003 .004 .004 .010 .011 .012 .017 .018 .019 .025 .025 .026 .032 .032 .033 .039 .040 .040 .046 .047 .048 .053 .054 .055 .061 .061 .062 .068 .069 .069 .075 .076 .077 .082 .083 .084 .089 .090 .091 .097 .097 .098 .104 .105 .105 .111.112 .113 」18.119 .120.126 .126 」27.133 .133 .134.140 .141 」41.147 .148.1497 8 9 .005 .006 .006 .012 .013 .014 .019 .020 .021 .027 .027 .028 .034 .035 .035 .041 .042 .043 .048 .049 .050 .056 .056 .057 .063 .063 .064 .070 .071 .071 .077 .078 .079 .084 .085 .086 .092 .092.093.099 」00」00 .106 .107 」07.113 .114.115.120」21」22 」28.128 」29 .135 .136 」36 .142 .143 」44 .149 .150」510.22 220 .159 .159 .160 .161 .162 .162 .163 .164 .164 .1650.23 230 .166 .167 .167 .168 .169 .170 .170 .171 .172 」72w/s W 0 1 2 3 4 5 6 7 8 90.24 240 .173 」74 .175 .175 .176 .177 .177 .178 .197 」800.25 250 ・180 .181 .182 .183 .183 .184 .185 .185 .186 」870.26 260 .188 .188 .189 .190 .190 .191 .192 .193 .193 」940.27 270 .195 .195 」9 .197 .198 .199 .199 .200 .201 .2010.28 280 3202 .203 .203 .204 .205 .205 .206 .207 .208 .2080.29 290 ・209 .210 .211 .211 .212 .213 .214 .214 .215 .2160.30 300 .216 .217 .218 .219 .219 .220 .221 .221 .222 .2230.31 310 .224 .224 .225 .226 .227 .227 .228 .229 .229 .2300.32 320 .231 .232 .232 .233 .234 .234 .235 .236 .237 .2370.33 330 .238 .239 .239 .240 .241 .242 .242 .243 .244 .2450.34 340 .245 .246 .247 .247 .248 .249 .250 .250 .251 .2520.35 350 .252 .253 .254 .255 .255 .256 .257 .257 .258 .2590.36 360 .260 .260 .261 .262 .263 .263 .264 .265 .265 .2660.37 370 .267 .268 .268 .269 .270 .270 .271 .272 .273 .2730.38 380 .274 .275 .275 .276 .277 .278 .278 .279 .280 .2810.39 390 .281 .282 .283 .283 .284 .285 .286 .286 .287 .2890.40 400 .288 .289 .290 .291 .291 .292 .293 .293 .294 .2950.41 410 .296 .296 .297 .298 .298 .299 .300 .301 .301 .3020.42 420 .303 .303 .304 .305 .306 .306 .307 .308 .308 .3090.43 430 .310 .311 .311 .312 .313 .314 .314 .315 .316 .3160.44 440 .317 .318 .319 .319 .320 .321 .321 .323 .323 .3240.45 450 .324 .325 .326 .326 .327 .328 .329 .329 .330 .3310.46 460 .331 .332 .333 .333 .334 .335 .336 .336 .337 .3380.47 470 .338 .339 .340 .341 .341 .342 .343 .343 .344 .3450.48 480 .346 .346 .347 .348 .348 .349 .350 .351 .351 .352 0.49 490 .353 .353 .354 .355 .355 .356 .357 .358 .358 .3590.50 500 .360 .360 .361 .362 .363 .363 .364 .365 .365 3.68W/S W 0 1 2 3 4 5 6 7 8 90.51 510 .367 .368 .368 .369 .370 .370 .371 372 372 .3730.52 520 .374 .375 .375 .376 .377 .377 .378 .379 .379 .3800.53 530 .381 .382 .382 .383 384 .384 .385 .386 .386 .3870.54 540 .388 .389 .389 .390 .391 .391 .392 .393 .393 .3940.55 550 .395 .396 .396 .397 .398 .398 .399 .400 .400 .401056 560 .402 .402 .403 .404 .405 .405 .406 .407 .407 .4080.57 570 .409 .409 .410 .411 .411 .412 .413 .414 .414 .4150.58 580 .416 .416 .417 .418 .418 .419 .420 .420 .421 .4220.59 590 .422 .423 .424 .425 .425 .426 .427 .427 .428 .4290.60 600 .429 .430 .431 .431 •432.433 .433 .434 .435 .4350.61 610 •436.437 .437 .438 .439 .439 .440 .441 .442 .4420.62 620 .443 .444 .444 .445 .446 .446 .447 448 .448 .4490.63 630 .450 .450 .451 .452 .452 .453 .454 454 .455 .4560.64 640 .456 .457 .458 .458 .459 .460 .460 461. .462 .4620.65 650 .463 .464 .464 .465 .466 .466 .467 468 .468 .4690.66 660 .470 .470 .471 .472 .472 .473 .474 .474 .475 .4760.67 670 .476 .477 .477 .478 .479 .479 .480 .481 .481 .4820.68 680 .483 .483 .484 .485 .485 .486 .487 .488 .488 .4890.69 690 .489 .490 .491 .491 .492 .492 .493 .494 .494 .4950.70 700 .496 .496 .497 .498 •498.499 .500 .500 .501 .5010.71 710 .502 .503 .503 .504 .505 .505 .506 .507 .507 .5080.72 720 .508 .509 .510 .510 .511 .512 .512 .513 .514 .5140.73 730 .515 .516 .516 .517 .517 .518 .519 .519 .520 .5200.74 740 .521 .522 .522 .523 .524 524 .525 .525 .526 .5270.75 750 .527 .528 .529 .529 .530 .530 .531 .532 .532 .533 0.76 760 .533 .534 .535 .535 .536 .537 .537 .538 .538 .539w样品厚度较厚：M =0.01-3.49见表W：样品厚度(um)： S：探针间距(mm)W/S0.00 0.01 0.020.03 0.040.00 0.0000 0.0072 0.0144 0.0216 0.0289 0.10 0.0721 0.0794 0.0866 0.0938 0.1010 0.20 0」443 0.1515 0.1587 0.1659 0.1731 0.30 0.2164 0.2236 0.2308 0.2380 0.2452 0.40 0.2884 0.2956 0.3027 0.3099 0.3171 0.50 0.3597 0.3668 0.3738 0.3808 0.3878 0.60 0.4293 0.4361 0.4429 0.4496 0.4563 0.70 0.4957 0.5021 0.5085 0.5148 0.5210 0.80 0.5576 0.5635 0.5694 0.5751 0.58090.90 0.6141 0.6194 0.6247 0.6299 0.63511.00 0.6647 0.6694 0.6741 0.6787 0.6833 1.10 0.7093 0.7134 0.7175 0.7215 0.7255 1.20 0.7482 0.7518 0.7553 0.7589 0.7622 1.30 0.7817 0.7848 0.7879 0.7908 0.79381.400.81060.8132 0.8158 0.8184 0.82091.50 0.8352 0.8375 0.8397 0.8419 0.8441 1.60 0.8563 0.8382 0.8601 0.8620 0.8639 1.70 0.8743 0.8760 0.8776 0.8792 0.8808 0.05 0.06 0.07 0.08 0.09 0.0361 0.0433 0.0505 0.0577 0.0649 0.1082 0.1154 0.1226 0.1298 0.13710.1803 0.1875 0.1948 0.2020 0.2092 0.2524 0.2596 0.2668 0.2740 0.2812 0.3242 0.3313 0.3385 0.3456 0.3526 0.3948 0.4018 0.4087 0.4156 0.4224 0.4630 0.4696 0.4762 0.4827 0.4892 0.5273 0.5334 0.5396 0.5456 0.5516 0.5866 0.5922 0.5978 0.6033 0.6087 0.6402 0.6452 0.6501 0.6551 0.6599 0.6877 0.6922 0.6965 0.7009 0.7051 0.7294 0.7333 0.7371 0.7408 0.7445 0.7666 0.7689 0.7122 0.7754 0.7786 0.7967 0.7996 0.8024 0.8052 0.80790.8234 0.82580.82820.8306 0.83290.8462 0.8483 0.8503 0.8524 0.8544 0.8657 0.8675 0.8692 0.8709 0.8726 0.8823 0.8838 0.8853 0.8868 0.88831.80 0.8897 0.8911 0.8925 0.8939 0.8952 0.8965 0.8978 0.8991 0.9004 0.90161.90 0.9029 0.9041 0.9053 0.9064 0.9076 0.9087 0.9099 0.9110 0.9121 0.9131w/s 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.092.00 0.9142 0.9152 0.9162 0.9172 0.9182 0.9192 0.9202 0.9211 0.9221 0.9230 2.10 0.9239 0.9248 0.9257 0.9266 0.9274 0.9283 0.9291 0.9299 0.9307 0.9315 2.20 0.9323 0.9331 0.9338 0.9346 0.9353 0.9361 0.9368 0.9375 0.9382 0.9389 2.30 0.9396 0.9402 0.9409 0.9415 0.9422 0.9428 0.9435 0.9441 0.9447 0.9453 2.40 0.9459 0.9402 0.9470 0.9476 0.9482 0.9487 0.9493 0.9498 0.9503 0.9509 2.50 0.9514 0.9519 0.9524 0.9529 0.9534 0.9538 0.9543 0.9548 0.9553 0.9557 2.60 0.9562 0.9566 0.9571 0.9575 0.9579 0.9583 0.9588 0.9592 0.9596 0.9600 2.70 0.9604 0.9608 0.9612 0.9616 0.9619 0.9623 0.9627 0.9630 0.9634 0.9637 2.80 0.9641 0.9644 0.9648 0.9652 0.9655 0.9658 0.9661 0.9664 0.9667 0.96712.90 0.9674 0.96 力0.9680 0.9683 0.9686 0.9689 0.9692 0.9694 0.9697 0.97003.00 0.9703 0.9705 0.9708 0.9711 0.9713 0.9716 0.9718 0.9721 0.9724 0.9726 3.10 0.9728 0.9731 0.9733 0.9736 0.9738 0.9740 0.9742 0.9745 0.9747 0.9749 3.20 0.9751 0.9753 0.9756 0.9758 0.9760 0.9762 0.9764 0.9766 0.9768 0.97703.30 0.9772 0.9774 0.9776 0.9778 0.9779 0.9781 0.9783 0.9785 0.9787 0.9788 3.40 0.9790 0.9792 0.9794 0.9795 0.9797 0.9799 0.9800 0.9802 0.9803 0.9805如需所测值更精确，请查下表附录2样品形状和测量位置的修正系数D (£ )(1)圆形薄片探针位置旦栓d 距圆心位置距边缘位置0mm 1/4 d 5 mm 4 mm 3 mm 2 mm20 0.9788 0.9633 0.9633 0.9508 0.9263 0.870223 0.9839 0.9719 0.9662 0.9538 0.9295 0.873925 0.9863 0.9761 0.9677 0.9553 0.9312 0.875827 0.9882 0.9794 0.9688 0.9565 0.9325 0.877330 0.9904 0.9832 0.9702 0.9580 0.9342 0.879332 0.9916 0.9852 0.9709 0.9588 0.9351 0.880435 0.9929 0.9876 0.9718 0.9598 0.9362 0.881738 0.9940 0.9894 0.9725 0.9606 0.9371 0.882940 0.9946 0.9904 0.9729 0.9610 0.9377 0.883542 0.9951 0.9913 0.9733 0.9614 0.9382 0.884145 0.9957 0.9924 0.9738 0.9620 0.9488 0.884950 0.9965 0.9938 0.9744 0.9627 0.9497 0.885955 0.9971 0.9919 0.9749 0.9633 0.9403 0.886857 0.9973 0.9952 0.9751 0.9635 0.9406 0.887160 0.9976 0.9957 0.9752 0.9638 0.9409 0.887563 0.9978 0.9961 0.9755 0.9640 0.9412 0.887965 0.9979 0.9963 0.9757 0.9641 0.9414 0.888170 0.9982 0.9968 0.9760 0.9645 0.9418 0.888675 0.9985 0.9972 0.9762 0.9648 0.9421 0.889180 0.9986 0.9976 0.9764 0.9650 0.9424 0.889590 0.9989 0.9981 0.9768 0.9654 0.9429 0.8901100 0.9991 0.9984 0.9770 0.9657 0.9433 0.8904（2）矩形薄片正方形矩形d/s a/d=l a/d=2 a/d=3 a/d$41.0 0.2204 0.22051.25 0.2751 0.27021.5 0.3263 0.3286 0.32861.75 0.3794 0.3803 0.38032.0 0.4301 0.4297 0.42972.5 0.5192 0.5194 0.51943.0 0.5422 0.5957 0.5958 0.59584.0 0.6870 0.7115 0.7115 0.71155.0 0.7744 0.7887 0.7888 0.78887.5 0.8846 0.8905 0.8905 0.890510.0 0.9312 0.9345 0.9345 0.934515.0 0.9682 0.9696 0.9696 0.969620.0 0.9788 0.9830 0.9860 0.983040.0 0.9955 0.9957 0.9957 0.9957100 1.0000 1.0000 1.0000 1.0000 d:短边长度a：长边长度S：探针间距提醒：每次开机启动，仪器会有一个自动校正和自动预热过程，初测试偶有5 到10次测试数值不精确视为正常情况。