当前位置：文档之家 › 最新四探针法测电阻率

最新四探针法测电阻率

  • 格式：doc
  • 大小：3.62 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

四探针法测电阻率

四探针法测电阻率

实验 四探针法测电阻率1．实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2．实验内容① 硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

② 薄层电阻率的测量：对不同尺寸的单面扩散片和双面扩散片的薄层电阻率进行测量。

改变条件进行测量（与①相同），对结果进行比较。

3． 实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法，四探针法，单探针扩展电阻法，范德堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

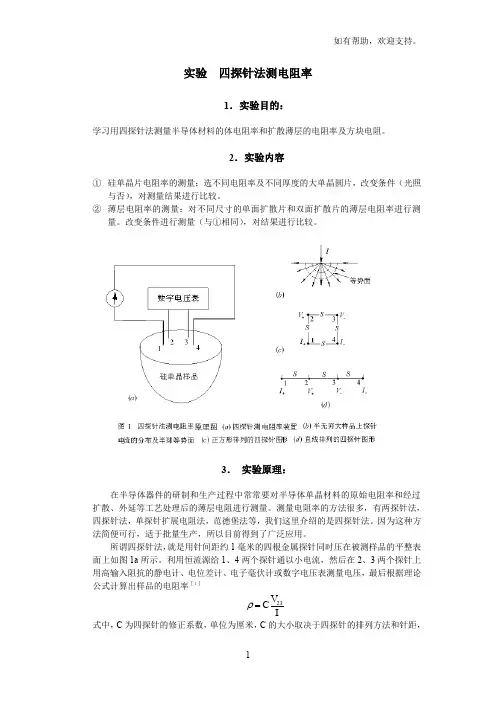
所谓四探针法，就是用针间距约1毫米的四根金属探针同时压在被测样品的平整表面上如图1a 所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用高输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算出样品的电阻率［１］IV C23=ρ 式中，C 为四探针的修正系数，单位为厘米，C 的大小取决于四探针的排列方法和针距，探针的位置和间距确定以后，探针系数C 就是一个常数；V 23为2、3两探针之间的电压，单位为伏特；I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相关，下面我们分两种情况来进行讨论。

⑴ 半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻率的装置；(b)为半无穷大样品上探针电流的分布及等势面图形；(c)和(d)分别为正方形排列及直线排列的四探针图形。

因为四探针对半导体表面的接触均为点接触，所以，对图１（b ）所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位面为图中虚线所示的半球面。

于是，样品电阻率为ρ，半径为r ，间距为dr 的两个半球等位面间的电阻为dr r dR 22πρ=， 它们之间的电位差为 dr r IIdR dV 22πρ==。

四探针测试电阻率实验指导

四探针测试电阻率实验指导
V( r ) I ………………………(2) 2 r
可以看到，探针 2 处的电势 V2 是处于探针点电流源+I 和处于探针 4 处的点
电流源-I 贡献之和，因此： I 1 1 V2 ( ) ………………… (3) 2 s 2s 同理，探针 3 处的电势 V3 为
V3 I 1 1 ( ) …………………… (4) 2 2s s
图 1 测量方阻的四探针法原理
对半无穷大均匀电阻率的样品， 若样品的电阻率为 ， 点电流源的电流为 I， 则当电流由探针流入样品时，在 r 处形成的电势 V( r ) 为
V( r ) I ………………………(1) 2 r
同理，当电流由探针流出样品时，在 r 处形成的电势 V( r ) 为
R 单位为 / 。可见， R 阻值大小与正方形的边长无关，故取名为方块电
阻，仅仅与薄膜的厚度有关。用等距直线排列的四探针法，测量薄层厚度 d 远小 于探针间距 s 的无穷大薄层样品，得到的电阻称之为薄层电阻。
图 2 薄层电阻示意图 在用四探针法测量半导体的电阻率时， 要求探头边缘到材料边缘的距离远远 大于探针间距，一般要求 10 倍以上；要在无振动的条件下进行，要根据被测对 象给予探针一定的压力， 否则探针振动会引起接触电阻变化。光电导和光电压效 应严重影响电阻率测量， 因此要在无强光直射的条件下进行测量。半导体有明显 的电阻率温度系数， 过大的电流会导致电阻加热，所以测量要尽可能在小电流条 件下进行。 高频讯号会引入寄生电流，所以测量设备要远离高频讯号发生器或者 有足够的屏蔽，实现无高频干扰。
实验名称：四探针法测量半导体的电阻率和方块电阻
一、 实验目的:
1．掌握四探针法测量半导体材料电阻率和方块电阻的基本原理。 2．掌握半导体电阻率和方块电阻的测量方法。 3. 掌握半导体电阻率和方块电阻的换算。 4．了解和控制各种影响测量结果的不利因素。

四探针测试仪测量薄膜电阻率

四探针测试仪测量薄膜电阻率

四探针测试仪测量薄膜的电阻率一、 实验目的1、掌握四探针法测量电阻率和薄层电阻的原理及测量方法；2、了解影响电阻率测量的各种因素及改进措施。

二、实验仪器采用SDY-5型双电测四探针测试仪（含：直流数字电压表、恒流源、电源、DC-DC 电源变换器）。

三、实验原理电阻率的测量是半导体材料常规参数测量项目之一。

测量电阻率的方法很多，如三探针法、电容---电压法、扩展电阻法等。

四探针法则是一种广泛采用的标准方法，在半导体工艺中最为常用。

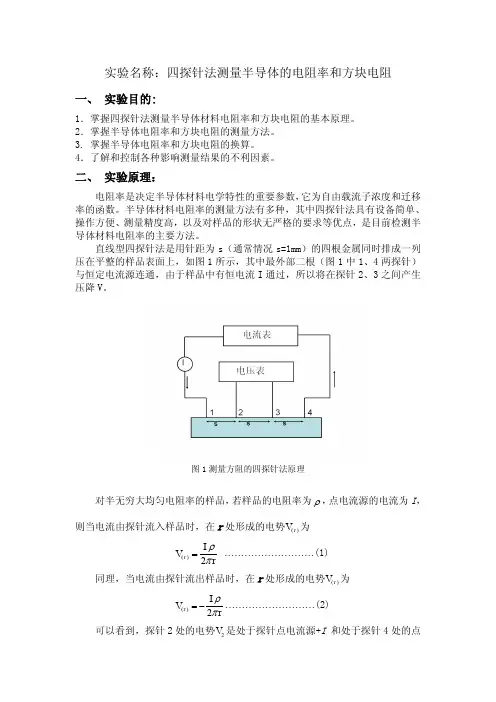
1、半导体材料体电阻率测量原理在半无穷大样品上的点电流源， 若样品的电阻率ρ均匀， 引入点电流源的探针其电流强度为I ，则所产生的电场具有球面的对称性， 即等位面为一系列以点电流为中心的半球面，如图1所示。

在以ｒ为半径的半球面上，电流密度ｊ的分布是均匀的：若E 为ｒ处的电场强度， 则：由电场强度和电位梯度以及球面对称关系， 则：取ｒ为无穷远处的电位为零， 则：（1）dr d E ψ-=dr r I Edr d 22πρψ-=-=⎰⎰⎰∞∞I -=-=)(022r rr r dr Edr d ψπρψr l r πρψ2)(=图3 四探针法测量原理图上式就是半无穷大均匀样品上离开点电流源距离为ｒ的点的电位与探针流过的电流和样品电阻率的关系式，它代表了一个点电流源对距离ｒ处的点的电势的贡献。

对图2所示的情形，四根探针位于样品中央，电流从探针1流入，从探针4流出， 则可将1和4探针认为是点电流源，由1式可知，2和3探针的电位为：2、3探针的电位差为： 此可得出样品的电阻率为：上式就是利用直流四探针法测量电阻率的普遍公式。

我们只需测出流过1、4 探针的电流I 以及2、3 探针间的电位差V 23，代入四根探针的间距， 就可以求出该样品的电阻率ρ。

实际测量中， 最常用的是直线型四探针（如图3所示），即四根探针的针尖位于同一直线上，并且间距相等， 设r 12=r 23=r 34=S ，则有：S IV πρ223= 需要指出的是： 这一公式是在半无限大样品的基础上导出的，实用中必需满足样品厚度及边缘与探针之间的最近距离大于四倍探针间距，这样才能使该式具有足够的精确度。

四探针法测量电阻率

四探针法测量电阻率
实验二 四探针法测量电阻率
一、引言 电阻率是反映半导体材料导电性能的重要参数之一.虽然测量电阻率的方法很多, 但由于四探针法设备简单、操作方便、精确度高、测量范围广，而且对样品形状无严 格要求，不仅能测量大块材料的电阻率，也能测量异形层、扩散层、离子注入层及外 延层的电阻率，因此在科学研究及实际生产中得到广泛利用。 本实验是用四探针法测量硅单晶材料的电阻率及 pn 结扩散层的方块电阻。通过 实验，掌握四探针法测量电阻率的基本原理和方法以及对具有各种几何形状样品的修 正，并了解影响测量结果的各种因素。 二、原理 1、 四探针法测量单晶材料的电阻率 最常用的四探针法是将四根金属探针的针尖排在同一直线上的直线型四探针法，如 图 2.1 所示。当四根探针同时压在一块相对于探针间距可视为半无穷大的半导体平坦表 面上时，如果探针接触处的材料是均匀的，并可忽略电流在探针处的少子注入，则当电 流 I 由探针流入样品时，可视为点电流源，在半无穷大的均匀样品中所产生的电力线具 有球面对称性，即等势面为一系列以点电流源为中心的半球面。样品中距离点电源 r 处 的电流密度 j，电场ε和电位 V 分别为
0
式中 q 为电子电荷，u 为扩散层中多数载流子的迁移率。因此，可引入扩散层平均电阻 率 ，可以证明，
R X j C 0
三、实验装置
V23 X j ............(15) I
实验装置主要由三部分组成：四探针头、电流调节装置、电压测试仪。 1、 四探针头 四根探针头要等距离地排列在一直线上，探针间距要固定（通常约为 1mm 左右） ， 游移度要小。探针头地曲率半径约为 50um 左右，探针之间的电绝缘性能要好。为了 使探针和样品形成较好的欧姆接触，要求探针与待测材料有较低的接触电势差，而且 探针和样品之间要加一定的压力（每根探针压力为 100－200g） 。因此，探针要用导电 性能好的硬质、耐磨金属制成，通常采用钨、碳化钨、锇铱合金、合金钢等。 2、 电流调节装置 四探针法的测试电路如图 2.2 所示。

四探针法测电阻率原理

四探针法测电阻率原理

四探针法测电阻率原理四探针法是一种常用的测量材料电阻率的方法，它通过在材料表面使用四根探针进行电阻率测量，可以得到较为准确的电阻率数值。

四探针法的原理相对简单，但是在实际操作中需要注意一些细节，下面将详细介绍四探针法测电阻率的原理及其操作步骤。

首先，让我们来了解一下四探针法的原理。

四探针法是利用四个电极进行电阻率测量的方法，其中两个电极用于加电流，而另外两个电极则用于测量电压。

通过这种方式，可以消除电极接触电阻对测量结果的影响，从而得到较为准确的电阻率数值。

在进行测量时，需要保持电流电极之间的距离小于电压电极之间的距离，以确保电流在电压电极之间均匀分布，从而避免测量误差。

在实际操作中，四探针法的测量步骤如下，首先，将四个探针分别插入待测材料表面，其中两个探针用于加电流，另外两个探针则用于测量电压。

接下来，通过外部电源向电流探针施加一定电流，同时使用电压表测量电压探针之间的电压。

根据欧姆定律，通过测量得到的电流和电压值，可以计算出材料的电阻率。

四探针法测量电阻率的优点在于可以消除电极接触电阻对测量结果的影响，从而得到较为准确的电阻率数值。

此外，四探针法适用于各种材料的电阻率测量，包括金属、半导体和导体等材料。

因此，四探针法在科研和工程领域中得到了广泛的应用。

总之，四探针法是一种常用的测量材料电阻率的方法，通过在材料表面使用四个探针进行电阻率测量，可以得到较为准确的电阻率数值。

在实际操作中，需要注意保持电流电极之间的距离小于电压电极之间的距离，以确保电流在电压电极之间均匀分布，从而避免测量误差。

四探针法测量电阻率的优点在于可以消除电极接触电阻对测量结果的影响，适用于各种材料的电阻率测量，因此在科研和工程领域中得到了广泛的应用。

四探针法测电阻率共14页

四探针法测电阻率共14页

实验四探针法测电阻率1．实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2．实验内容①硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

②薄层电阻率的测量：对不同尺寸的单面扩散片和双面扩散片的薄层电阻率进行测量。

改变条件进行测量（与①相同），对结果进行比较。

3．实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法，四探针法，单探针扩展电阻法，范德堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

所谓四探针法，就是用针间距约1毫米的四根金属探针同时压在被测样品的平整表面上如图1a所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用高输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算出样品的电阻率［１］式中，C为四探针的修正系数，单位为厘米，C的大小取决于四探针的排列方法和针距，探针的位置和间距确定以后，探针系数C 就是一个常数；V 23为2、3两探针之间的电压，单位为伏特；I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相关，下面我们分两种情况来进行讨论。

⑴ 半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻率的装置；(b)为半无穷大样品上探针电流的分布及等势面图形；(c)和(d)分别为正方形排列及直线排列的四探针图形。

因为四探针对半导体表面的接触均为点接触，所以，对图１（b ）所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位面为图中虚线所示的半球面。

于是，样品电阻率为ρ，半径为r ，间距为dr 的两个半球等位面间的电阻为 它们之间的电位差为 dr r IIdR dV 22πρ==。

四探针法测量半导体电阻率及薄层电阻

四探针法测量半导体电阻率及薄层电阻

在半无穷大样品上的点电流源， 若样品的电阻率ρ均匀， 引入点电流源的探针其电流
强度为 I，则所产生的电力线具有球面的对称性， 即等位面为一系列以点电流为中心的半
球面，如图 2-1 所示。在以ｒ为半径的半球面上，电流密度ｊ的分布是均匀的：
j= I 2πr 2
（2-1）
若 E 为ｒ处的电场强度， 则
E = jρ = Iρ 2πr2
2
r12
1 r13
3
r34
4
r24
ss s
12
3
4
图 2-2 任意位置的四探针
图 2-3 直线型四探针
ρ = V23 2πS I
（2-9）
2-9 式就是常见的直流四探针 (等间距) 测量电阻率的公式， 也是本实验要用的测量公式之 一。需要指出的是： 这一公式是在半无限大样品的基础上导出的，实用中必需满足样品厚度 及边缘与探针之间的最近距离大于四倍探针间距， 这样才能使该式具有足够的精确度。
包围。同样需要注意的是当片状样品不满足极薄样品的条件时，仍需按式(2.10)计算电阻
率P。其修正系数Bo列在表 2.3 中。
2. 扩散层的薄层电阻
半导体工艺中普遍采用四探针法测量扩散层的薄层电阻，由于反向 pn 结的隔离作
用，扩散层下的衬底可视为绝缘层，对于扩散层厚度(即结深 Xj)远小于探针间距 S，而横
向尺寸无限大的样品，则薄层电阻率为：
s d
d 2d
ρ = 2π s × V
B0
I
s d
B0
s d
0.1
1.0009
0.6
B0
s d
1.1512
1.2
B0 1.7329
0.2

四探针测试方块电阻或电阻率的实验步骤

四探针测试方块电阻或电阻率的实验步骤

半导体物理四探针测试方块电阻或电阻率的实验步骤
1．打开背后电源，预热30min
2．操作面板“恒流源”按钮按下，选择电阻率/方阻正测/反测电流选择1 0mA档
3．放上样品，注意不要碰上样品表面，避免沾污
4．调节测试架下旋旋钮使探针轻按在样品上，听到响声，表示针和样品已经接触上
电阻率测试：电阻率灯亮
5．根据样品厚度，找到对应电流值，调节粗调，细调使得电流表读数为表上具体厚度所对应的电流值。

6．选择合适的“电流选择”0.1mA 1mA 10mA/100mA,使得电压表有效值为3位，即为测试的电阻率
方块电阻测试：方块电阻灯亮
7．电流值为45.32mA，选择合适的“电流选择”0.1mA 1mA 10mA/100mA,使得电压表有效值为3位，即为测试的方块电阻。

利用直流四探针法测量半导体的电阻率

利用直流四探针法测量半导体的电阻率

利用直流四探针法测量半导体的电阻率一、测试原理：当四根金属探针排成一条直线，并以一定压力压在半导体材料上时，在1,4两根探针间通过电流Ｉ，则2,3探针间产生电位差Ｖ（如图所示）。

根据公式可计算出材料的电阻率：其中，C 为四探针的探针系数（cm ），它的大小取决于四根探针的排列方法和针距。

二、仪器操作：（一）测试前的准备：1、将电源插头插入仪器背面的电源插座，电源开关置于断开位置；2、工作方式开关置于“短路”位置，电流开关处于弹出位置；3、将手动测试架的屏蔽线插头与电气箱的输入插座连接好；4、对测试样品进行一定的处理（如喷沙、清洁等）；5、调节室内温度及湿度使之达到测试要求。

（二）测试：首先将电源开关置于开启位置，测量选择开关置于“短路”，出现数字显示，通电预热半小时。

1、放好样品，压下探头，将测量选择开关置于“测量”位置，极性开关置于开关上方；2、选择适当的电压量程和电流量程，数字显示基本为“0000”，若末位有数字，可旋转调零调节旋钮使之显示为“0000”；3、将工作方式开关置于“I 调节”，按下电流开关，旋动电流调节旋钮，使数字显示为“1000”，该值为各电流量程的满量程值；4、再将极性开关压下，使数显也为1000±1，退出电流开关，将工作方式开关置于1或6.28处（探头间距为1.59mm 时置于1位置，间距为1mm 时置于6.28位置）；（调节电流后，上述步骤在以后的测量中可不必重复；只要调节好后，按下电流开关，可由数显直接读出测量值。

）5、若数显熄灭，仅剩“1”，表示超出该量程电压值，可将电压量程开关拨到更高档；IV C 3,2=ρ6、读数后，将极性开关拨至另一方，可读出负极性时的测量值，将两次测量值取平均数即为样品在该处的电阻率值。

三、注意事项：1、压下探头时，压力要适中，以免损坏探针；2、由于样品表面电阻可能分布不均，测量时应对一个样品多测几个点，然后取平均值；3、样品的实际电阻率还与其厚度有关，还需查附录中的厚度修正系数，进行修正。

四探针法测电阻率原理

四探针法测电阻率原理

四探针法测电阻率原理
四探针法测电阻率是一种常用的电学测量方法，它可以准确测量材料的电阻率。

该方法利用四个电极分别组成的探针来接触被测物质表面，通过施加电流和测量电压来计算电阻率。

该方法的原理基于欧姆定律，即电流通过导体时，电流与电压成正比，比例常数为电阻。

测量时，我们使用两个电流探针在被测物质上施加电流，而另外两个电压探针则用于测量电压。

根据欧姆定律，电流与电压之间的比值即可得到电阻。

为了提高测量的准确性和稳定性，四个电极的排列方式很重要。

通常，两个电流探针之间应隔有一定距离，以避免电流从一个探针跳过直接到另一个探针而影响测量结果。

同样，两个电压探针之间也应保持一定距离，以避免电压的变化受到相邻电极的影响。

在测量过程中，我们需要保持恒定的电流，并测量对应的电压。

通过改变施加的电流大小，我们可以获得多组电流-电压的测
量数据。

然后，根据这些数据，可以绘制出电流-电压的关系
曲线。

该曲线的斜率即为被测物质的电阻率。

通过四探针法测电阻率，我们可以得到材料的电阻率值，这对于研究材料的电性质、导电性等具有重要意义。

四探针测试半导体的电阻率

四探针测试半导体的电阻率

四探针法测量半导体的电阻率一、实验目的1、了解四探针电阻率测试仪的基本原理；2、了解的四探针电阻率测试仪组成、原理和使用方法；3、能对给定的物质进行实验，并对实验结果进行分析、处理。

二、实验原理1.电阻的测量电性能是材料的重要物理性能之一，材料导电性的测量就是测量试样的电阻或电阻率。

电阻的测量方法很多，若精度要求不高，常用兆欧表、万用表、欧姆表及伏安法等测量；若精度要求比较高或阻值在10-6～102Ω的材料电阻（如金属或合金的阻值）测量时，需采用更精密的测量方法。

常用的几种方法如下：①双臂电桥法：根据被测量与已知量在直流桥式线路上进行比较而得出测量结果，其精确测量电阻范围为10-6～10-3Ω，误差为0.2～0.3%。

缺点：受环境温度影响较大。

②直流电位计测量法：一种比较法测量电动势，通过“串联电路中电压与电阻成正比”计算得出电阻。

其可测量10-7V微小电动势。

优点：导线和引线电阻不影响测试结果。

③直流四探针法：主要用于半导体或超导体等低电阻率的精确测量。

④冲击检流计法：主要用于绝缘体电阻的测量，将待测电阻与电容器串联，用冲击检流计测量电容器极板上的电量。

通过检流计的偏移量来计算待测电阻，可测得绝缘体电阻率高达1015～1016Ω·cm。

2.电阻率的测量电阻率是用来表示各种物质电阻特性的物理量，某种材料制成的长1米、横截面积是1平方毫米的在常温下（20℃时）导线的电阻，叫做这种材料的电阻率。

它反映物质对电流阻碍作用。

电阻率是半导体材料的重要电学参数之一，硅单晶的电阻率与半导体器件的性能有密切联系。

因此电阻率的测量是半导体材料常规参数测量项目之一。

测量电阻率的方法很多，如二探针法、扩展电阻法等。

而四探针法则是目前检测半导体电阻率的一种广泛采用的标准方法。

它具有设备简单、操作方便、精度较高、对样品的几何形状无严格要求等优点。

3.直流四探针法测试原理①体电阻率测量：当1、2、3、4根金属探针排成直线时，并以一定的压力压在半导体材料上，在1、4两处探针间通过电流I，则2、3探针间产生电位差V。

四探针法测量电阻率

四探针法测量电阻率

实验二 四探针法测量电阻率一、引言电阻率是反映半导体材料导电性能的重要参数之一.虽然测量电阻率的方法很多,但由于四探针法设备简单、操作方便、精确度高、测量范围广，而且对样品形状无严格要求，不仅能测量大块材料的电阻率，也能测量异形层、扩散层、离子注入层及外延层的电阻率，因此在科学研究及实际生产中得到广泛利用。

本实验是用四探针法测量硅单晶材料的电阻率及pn 结扩散层的方块电阻。

通过实验，掌握四探针法测量电阻率的基本原理和方法以及对具有各种几何形状样品的修正，并了解影响测量结果的各种因素。

二、原理1、 四探针法测量单晶材料的电阻率最常用的四探针法是将四根金属探针的针尖排在同一直线上的直线型四探针法，如图2.1所示。

当四根探针同时压在一块相对于探针间距可视为半无穷大的半导体平坦表面上时，如果探针接触处的材料是均匀的，并可忽略电流在探针处的少子注入，则当电流I 由探针流入样品时，可视为点电流源，在半无穷大的均匀样品中所产生的电力线具有球面对称性，即等势面为一系列以点电流源为中心的半球面。

样品中距离点电源r 处的电流密度j，电场ε和电位V 分别为)3........(..........2)2.........(2)1.......(. (22)2r I V r I j r Ij πρπρσεπ====其中，σ和ρ分别是样品的电导率和电阻率。

若电流由探针流出样品，则有)4........(..........2rI V πρ=因此，当电流由探针1流入样品，自探针4流出样品时，根据电位叠加原理，在探针2处的电位为)5.....(. (12123)212S S I S I V +⋅-⋅=πρπρ 在探针3处的电位为)6.....(. (12123)213S I S S I V ⋅-+⋅=πρπρ 式中的S 1是探针1和2之间的距离，S2是探针2和3之间的距离，S3是探针3和4之间的距离。

所以探针2、3之间的电位为)7......(S 1S S 1S S 1S 1(2I V V V 3213213223++-+-⋅πρ=-= 由此可求出样品的电阻率为)8.....(..........)S 1S S 1S S 1S 1(I V 2132132123-++-+-π=ρ 当S1＝S2＝S3＝S 时，（8）式简化为)9.....(. (223)IV Sπρ= （9）式就是利用直线型四探针测量电阻率的公式。

四探针法测量半导体电阻率及薄层电阻

四探针法测量半导体电阻率及薄层电阻

四探针法测量半导体电阻率及薄层电阻【实验目的】1、掌握四探针测量半导体材料电阻率和薄层电阻的测量原理及方法；2、针对不同几何形状的样品，掌握其修正方法；3、测试给定的三块不同规格样品数据，使用EXCEL软件对样品的数据进行计算和处理，如电阻率、方块电阻、标准差、不均匀度，画出电阻率波动图【实验原理】1. 半导体材料的电阻率在半无穷大样品上的点电流源，若样品的电阻率ρ均匀，引入点电流源的探针其电流强度为I，则所产生的电力线具有球面的对称性，即等位面为一系列以点电流为中心的半球面，如图1所示。

在以ｒ为半径的半球面上，电流密度ｊ的分布是均匀的：(1)图1 半无穷大样品点电流源的半球等位面若E为ｒ处的电场强度，则（2）由电场强度和电位梯度以及球面对称关系，则（3）(4)取ｒ为无穷远处的电位为零，则(5)(6)上式就是半无穷大均匀样品上离开点电流源距离为ｒ的点的电位与探针流过的电流和样品电阻率的关系式，它代表了一个点电流源对距离ｒ处点的电势的贡献。

对于图2所示的情形，四根探针位于样品中央，电流从探针1流入，从探针4流出，则可将1和4探针认为是点电流源，由(6)式可知，2和3探针的电位为1、3探针的电位差为：(7)由此可得出样品的电阻率为：(8)(8)式就是利用直流四探针法测量电阻率的普遍公式。

我们只需测出流过1 4 探针的电流I 以及2 3 探针间的电位差V 2 3，代入四根探针的间距，就可以求出该样品的电阻率ρ。

实际测量中，最常用的是直线型四探针， 即四根探针的针尖位于同一直线上，并且间距相等，如图3所示。

设 r 12 = r 23 = r 34 = S ，则有：(9)图2 任意位置的四探针 图3 直线型四探针（9）式就是常见的直流四探针 (等间距) 测量电阻率的公式， 也是本实验要用的测量公式之一。

需要指出的是： 这一公式是在半无限大样品的基础上导出的，实用中必需满足样品厚度及边缘与探针之间的最近距离大于四倍探针间距， 这样才能使该式具有足够的精确度。

四探针方法测电阻率

四探针方法测电阻率

的测量，如电导率、迁移率等，为材料科学和电子学等领域的研究提供
更多有价值的数据。
THANKS
感谢观看
导线
用于连接测试设备和样品，需选用低 阻抗导线。
实验环境与条件
01
02
03
实验室环境
保持实验室温度、湿度和 清洁度等环境因素稳定， 以保证测量结果的准确性。
电源条件
确保电源电压稳定，避免 电压波动对测量结果的影 响。
安全措施
实验操作过程中需注意安 全，遵守实验室安全规定， 确保实验人员和设备的安 全。
07
结论与展望
研究结论
1 2
电阻率测量精ቤተ መጻሕፍቲ ባይዱ高
四探针方法通过四个探针同时接触样品，能够有 效地减小接触电阻和测量误差，从而获得更高的 电阻率测量精度。
适用范围广
四探针方法适用于各种不同类型和规格的样品， 如金属、半导体、陶瓷等，具有较广的适用范围。
3
操作简便
四探针方法不需要对样品进行特殊处理或制备， 只需将探针放置在样品上即可进行测量，操作简 便易行。
随着科技的发展，四探针方法的应用领域不断拓展，不仅局限于半导体和金属材料检测。
在新能源领域，如太阳能电池和燃料电池的生产过程中，四探针方法可用于检测材料的电阻 率，提高电池性能和稳定性。
在环境监测领域，四探针方法可应用于土壤电阻率的测量，为土壤污染治理和土地资源管理 提供依据。此外，在地质勘探、生物医学和食品检测等领域，四探针方法也展现出广阔的应 用前景。
的测量。
四探针的优点与局限性
优点
四探针法具有较高的测量精度和稳定 性，适用于各种形状和尺寸的样品， 且操作简便、快速。
局限性
四探针法需要与被测材料直接接触， 可能会对材料表面造成损伤或污染； 同时对于导电性较差或不均匀的材料 ，测量结果可能存在误差。

四探针法测电阻率

四探针法测电阻率

实验一 四探针法测电阻率引言电阻率是反映半导体材料导电性能的重要参数之一。

测量电阻串的方法很多，四探针法是一种广泛采用的标准方法。

它的优点是设备简屯操作方便，精确度向，对样品的形状无严格要求。

本实验的目的是：掌握四探针测试电阻率的原理、方法和关于样品几何尺寸的修正，并了解影响测试结果的因素。

原理在一块相对于探针间距可视力半无穷大的均匀电阻率的样品上，有两个点电流源1、4。

电流由1流入，从4流出。

2、3是样品上另外两个探针的位置，它们相对于1、4两点的距离分别为、、、，如图1所示。

在半无穷大的均匀样品上点电流源所产生的电力线具有球面对称性，即等势面为一系列以点电流源为中心的半球面，如图2所示。

12r 42r 13r 43r图1 位置任意的是探针 图2 半无穷大样品上点电流源的半球等势面 若样品电阻率为ρ，样品电流为I ，则在离点电流源距离为r 处的电流密度J 为：22r I J π=（1） 又根据ρε=J （2）其中，ε为r 处的电场强度，有（1）、（2）式得22rI πρε= （3） 根据电场强度和电势梯度得关系及球面对称性可得 drdV −=ε 取r 为无穷远处得电势V 为零，则有 ∫∫∞−=r r V dr dV ε)(0r I r V 12)(πρ= （4）式（4）代表一个点电流源对距r 处点的点势的贡献。

在图1的情况，2、3两点的电势应为1、4两个相反极性的电电流源的共同贡献，即：11(242122r r I V −=πρ （5） )11(243133r r I V −=πρ （6）2、3两点的电势差为)1111(2431342122r r r r I V +−−=πρ 由此可以得出样品的电阻率为：1111(24313421223r r r r I V +−−=πρ （7）这就是利用四探针法测量电阻率的普遍公式。

只需测出流过1、4探针的电流；2、3探针间的电势差以及四根探针之间的距离，就可利用（7）式求出样品的电阻率。

四探针法测电阻率原理

四探针法测电阻率原理

四探针法测电阻率原理
四探针法是一种用来测量材料电阻率的方法，它可以准确地测量材料的电阻率，并且不受接触电阻的影响。

四探针法的原理是利用四个探针分别施加电流和测量电压，通过测量电流和电压的关系来计算材料的电阻率。

首先，我们来了解一下四探针法的原理。

四探针法利用四个探针，其中两个探针用来施加电流，另外两个探针用来测量电压。

这样可以避免接触电阻对测量结果的影响，提高了测量的准确性。

当电流通过材料时，会在材料内部产生电压梯度，通过测量这个电压梯度和电流的关系，可以计算出材料的电阻率。

其次，四探针法的测量步骤包括，首先，将四个探针分别插入材料表面，两个探针用来施加电流，另外两个探针用来测量电压。

然后，施加一个稳定的电流，并测量两个测量探针之间的电压。

根据欧姆定律，电阻率可以通过电流和电压的比值来计算得出。

四探针法的优点是可以准确地测量材料的电阻率，而且不受接触电阻的影响。

这种方法适用于各种材料，包括金属、半导体和绝缘体。

而且，由于四探针法可以避免接触电阻的影响，所以可以测
量非常小的电阻率，提高了测量的灵敏度。

总之，四探针法是一种准确测量材料电阻率的方法，它可以避免接触电阻的影响，提高了测量的准确性和灵敏度。

这种方法适用于各种材料，是一种非常重要的电学测量方法。

四探针方法测电阻率(原理公式推导)

四探针方法测电阻率(原理公式推导)
探针方法测量半导体的电阻率
〈一〉实验目的
〈二〉实验原理
〈三〉仪器结构特征
〈四〉操作步骤
〈五〉注意事项
〈六〉技术参数
<一> 实验目的
1、理解四探针方法测量半导体电阻率的原理； 2、学会用四探针方法测量半导体电阻率。
<二> 实验原理
1、体电阻率测量：
当１、２、３、４四根 金属探针排成一直线时， 并以一定压力压在半导体 材料上，在１、４两处探 针间通过电流I，则２、３
• 为克服测试时探针与样品接触时产生的接触
电势和整流效应的影响。本仪器设立有“粗 调”、“细调”调零电路能产生一个恒定的 电势来补偿附加电势的影响。 • 仪器自较电路中备有精度为0.02％、阻值为 19.96的标准电阻,作为自校电路的基础，通 过自校电路可以方便地对数字电压表精度和 恒流源进行校准。
在半导体材料断面测量时：直径范围
Φ15~100mm，其高度为400mm，如果要对大
于400mm长单晶的断面测量，可以将座体的
V型槽有机玻璃板取下，座体设有一个腰形
孔，用户可以根据需要增设支衬垫块使晶体
长度向台下延伸，以满足测量长单晶需求，
测试架有专门的屏蔽导线插头与电气箱联结。
<四> 实验步骤
1、测试准备：电源开关置于断开位置，工作 选择置于“短路”，电流开关处于弹出切断 位置。将测试样品放在样品架上，调节高度 手轮，使探针能与其表面保持良好接触。
• 温度影响电阻率,从面影响电阻 • p=p1(1+aT),p1为该材料0摄氏度时的电阻 率, a叫电阻的温度系数,不同材料的电阻 温度系数不同 • 由R=p*l/s p=p1(1+aT),得 • R=R1(1+aT) 同理,R1为0摄氏度时的电阻 • R=p*l/s(p—电阻率查表求；l—电阻长度 ；s—与电流垂直的电阻截面面

四探针方法测电阻率(原理公式推导)

四探针方法测电阻率(原理公式推导)
若电流取I = C 时，则ρ＝V，可由数字电压表直 接读出。
Page 5
温度影响电阻率,从面影响电阻 p=p1(1+aT),p1为该材料0摄氏度时的电阻率, a叫电阻
的温度系数,不同材料的电阻温度系数不同 由R=p*l/s p=p1(1+aT),得 R=R1(1+aT) 同理,R1为0摄氏度时的电阻 R=p*l/s(p—电阻率查表求；l—电阻长度；s—与电流
4、将工作选择档置于“自校”，使电流显示出“１９９＊”， 各量程数值误差为４字。
5、将工作选择档置于“调节”，电流调节在I＝6.28=C，C为 探针几何修正系数。
Page 16
1.显示板 2、单位显示灯 3、电流量程开关 4、工作选择开关 （短路、测量、调节、自校选择）5、电压量程开关6、输入插 座7、调零细调8、调零粗调9、电流调节10、电源开关11、电 流选择开关 12、极性开关
<三> 仪器结构特征
数字式四探针测试仪主体部分由高灵敏度直流数字电 压表、恒流源、电源、DC-DC电源变换器组成。为了 扩大仪器功能及方便使用，还设立了单位、小数点自 动显示电路、电流调节、自校电路和调零电路。
Page 11
仪器电源经过DC-DC变换器，由恒流源电路产生一个高稳定 恒定直流电流，其量程为10μA、100μA、1mA、10mA、 100mA，数值连续可调，输送到１、４探针上，在样品上 产生一个电位差，此直流电压信号由２、３探针输送到电气 箱内。具有高灵敏度、高输入阻抗的直流放大器中将直流信 号放大（放大量程有0.2mV、2mV、20mV 、200mV、 2V），再经过双积分A/D变换将模拟量变换为数字量，经由 计数器、单位、小数点自动转换电路显示出测量结果。
当圆形硅片的厚度满足W/S＜0.5时，电阻率为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

四探针法测电阻率实验四探针法测电阻率1．实验目的：学习用四探针法测量半导体材料的体电阻率和扩散薄层的电阻率及方块电阻。

2．实验内容①硅单晶片电阻率的测量：选不同电阻率及不同厚度的大单晶圆片，改变条件（光照与否），对测量结果进行比较。

②薄层电阻率的测量：对不同尺寸的单面扩散片和双面扩散片的薄层电阻率进行测量。

改变条件进行测量（与①相同），对结果进行比较。

3．实验原理：在半导体器件的研制和生产过程中常常要对半导体单晶材料的原始电阻率和经过扩散、外延等工艺处理后的薄层电阻进行测量。

测量电阻率的方法很多，有两探针法，四探针法，单探针扩展电阻法，范德堡法等，我们这里介绍的是四探针法。

因为这种方法简便可行，适于批量生产，所以目前得到了广泛应用。

所谓四探针法，就是用针间距约1毫米的四根金属探针同时压在被测样品的平整表面上如图1a 所示。

利用恒流源给1、4两个探针通以小电流，然后在2、3两个探针上用高输入阻抗的静电计、电位差计、电子毫伏计或数字电压表测量电压，最后根据理论公式计算出样品的电阻率［１］IV C23=ρ 式中，C 为四探针的修正系数，单位为厘米，C 的大小取决于四探针的排列方法和针距，探针的位置和间距确定以后，探针系数C 就是一个常数；V 23为2、3两探针之间的电压，单位为伏特；I 为通过样品的电流，单位为安培。

半导体材料的体电阻率和薄层电阻率的测量结果往往与式样的形状和尺寸密切相关，下面我们分两种情况来进行讨论。

⑴ 半无限大样品情形图1给出了四探针法测半无穷大样品电阻率的原理图，图中(a)为四探针测量电阻率的装置；(b)为半无穷大样品上探针电流的分布及等势面图形；(c)和(d)分别为正方形排列及直线排列的四探针图形。

因为四探针对半导体表面的接触均为点接触，所以，对图１（b ）所示的半无穷大样品，电流I 是以探针尖为圆心呈径向放射状流入体内的。

因而电流在体内所形成的等位面为图中虚线所示的半球面。

于是，样品电阻率为ρ，半径为r ，间距为dr 的两个半球等位面间的电阻为dr rdR 22πρ=， 它们之间的电位差为 dr r IIdR dV 22πρ==。

考虑样品为半无限大，在r →∞处的电位为0，所以图１（a ）中流经探针１的电流I 在r 点形成的电位为 ()rIdr r I V rr πρπρ2221==⎰∞。

流经探针１的电流在２、３两探针间形成的电位差为()⎪⎪⎭⎫⎝⎛-=1312123112r r I V πρ； 流经探针４的电流与流经探针１的电流方向相反，所以流经探针４的电流I 在探针２、３之间引起的电位差为()⎪⎪⎭⎫⎝⎛--=4342423112r r I V πρ。

于是流经探针１、４之间的电流在探针２、３之间形成的电位差为⎪⎪⎭⎫⎝⎛+--=4342131********r r r r I V πρ。

由此可得样品的电阻率为()11111214342131223-⎪⎪⎭⎫⎝⎛+--=r r r r I V πρ上式就是四探针法测半无限大样品电阻率的普遍公式。

在采用四探针测量电阻率时通常使用图１（c ）的正方形结构（简称方形结构）和图１（d ）的等间距直线形结构，假设方形四探针和直线四探针的探针间距均为S ，则对于直线四探针有 S r r S r r 2,42134312====()2223IV S ⋅=∴πρ对于方形四探针有 S r r S r r 2,42134312====⑵ 无限薄层样品情形()322223IV S ⋅-=∴πρ当样品的横向尺寸无限大，而其厚度t 又比探针间距S 小得多的时候，我们称这种样品为无限薄层样品。

图２给出了用四探针测量无限薄层样品电阻率的示意图。

图中被测样品为在p 型半导体衬底上扩散有n 型薄层的无限大硅单晶薄片，１、２、３、４为四个探针在硅片表面的接触点，探针间距为S ，n 型扩散薄层的厚度为t ，并且t<<S ，I +表示电流从探针１流入硅片，I -表示电流从探针４流出硅片。

与半无限大样品不同的是，这里探针电流在n 型薄层内近似为平面放射状，其等位面可近似为圆柱面。

类似前面的分析，对于任意排列的四探针，探针１的电流I 在样品中r 处形成的电位为()r tI dr rt I V rr ln 221πρπρ-==⎰∞式中ρ为n 型薄层的平均电阻率。

于是探针１的电流I 在２、３探针间所引起的电位差为()12131312123ln 2ln2r r t I r r tIV πρπρ=-= 同理，探针４的电流I 在２、３探针间所引起的电位差为()4342423ln 2r r t I V πρ=所以探针１和探针４的电流I 在２、３探针之间所引起的电位差是1243134223ln 2r r r r t I V ⋅⋅=πρ 于是得到四探针法测无限薄层样品电阻率的普遍公式为()4ln 21243134223r r rr I tV ⋅⋅=πρ对于直线四探针，利用S r rS r r 2,42134312====可得()52ln 2ln 222323IV t I tV ⋅==ππρ对于方形四探针，利用S r r S r r 2,42134312====可得()62ln 223IV t ⋅=πρ在对半导体扩散薄层的实际测量中常常采用与扩散层杂质总量有关的方块电阻R S ，它与扩散薄层电阻率有如下关系：jXjS NX q NdXq X R jμμρ110===⎰这里X j 为扩散所形成的pn 结的结深。

这样对于无限薄层样品，方块电阻可以表示如下： 直线四探针：()72ln 23IV X R jS πρ==方形四探针：()82ln 223IV X R jS πρ==在实际测量中，被测试的样品往往不满足上述的无限大条件，样品的形状也不一定相同，因此常常要引入不同的修正系数。

实际测量中的扩散样片可能有两种情况：单面扩散片和双面扩散片，如图3所示。

这两种样品的修正系数分别列于附录中的表。

图4 SZT-2A四探针测试仪4．实验装置及注意事项⑴实验装置实验装置如图4所示。

电路中的恒流源所提供的电流是连续可调的，电压表采用电位差计或数字电压表。

实验所用的探针通常采用耐磨的导电硬质合金材料，如钨、碳化钨等。

探针要求等间距配置，并使其具有很小的游移误差。

在探针上需加上适当的压力，以减小探针与半导体材料之间的接触电阻。

⑵注意事项①半无限大样品是指样品厚度及任意一根探针距样品最近边界的距离远大于探针间距，如果这一条件不能得到满足则必需进行修正。

②为了避免探针处的少数载流子注入，提高表面复合速度，待测样品的表面需经粗砂打磨或喷砂处理。

③在测量高阻材料及光敏材料时需在暗室或屏蔽盒内进行。

④因为电场太大会使载流子的迁移率下降，导致电阻率测量值增大，故须在电场强度E<1V/cm的弱场下进行测量。

⑤ 为了避免大电流下的热效应，测试电流应尽可能低，但须保证电压的测试精度。

不同电阻率样品的电流选择大致为[2]电阻率范围（Ω· cm ） 测量电流（mA ）<0.012 100 0.08~0.6 10 0.4~60 1 40~1200 0.1 >8000.01⑥ 为了满足探针与半导体的接触为欧姆接触，探针上须加上一定的压力。

对于体材料，一般取1~2kg ；对于薄层材料或外延材料选取200g 。

⑦ 当室温有较大波动时，最好将电阻率折算到23℃时的电阻率。

因为半导体的电阻率对温度很敏感。

如果有必要考虑温度对电阻率的影响，可用下面的公式进行计算()[]()91参考平均参考T T C T --=ρρ式中ρ参考为修正到某一参考温度(例如23℃)下的样品电阻率; ρ平均为测试温度下样品的平均电阻率；C T 为温度系数，它随电阻率变化的曲线示于图5；T 为测试温度；T 参考为某一指定的参考温度。

5．附录附录1A 样品厚度修正系数G （WS）样品厚度较薄：WS =0.001~1 见表5W ：样品厚度（μm ）：S ：探针间距（mm ）W/S W 0 1 2 3 4 5 6 7 8 9 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.190 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190.000 .007 .014 .022 .029 .036 .043 .051 .058 .065 .072 .079 .087 .094 .101 .108 .115 .123 .130 .137.001 .008 .015 .022 .030 .037 .044 .051 .058 .066 .073 .080 .087 .095 .102 .109 .116 .123 .131 .138.001 .009 .016 .023 .030 .038 .045 .052 .059 .066 .074 .081 .088 .095 .102 .110 .117 .124 .131 .139.002 .009 .017 .024 .031 .038 .045 .053 .060 .067 .074 .082 .089 .096 .103 .110 .118 .125 .132 .139.003 .010 .017 .025 .032 .039 .046 .053 .061 .068 .075 .082 .089 .097 .104 .111 .118 .126 .133 .140.004 .011 .018 .025 .032 .040 .047 .054 .061 .069 .076 .083 .090 .097 .105 .112 .119 .126 .133 .141.004 .012 .019 .026 .033 .040 .048 .055 .062 .069 .077 .084 .091 .098 .105 .113 .120 .127 .134 .141.005 .012 .019 .027 .034 .041 .048 .056 .063 .070 .077 .084 .092 .099 .106 .113 .120 .128 .135 .142.006 .013 .020 .027 .035 .042 .049 .056 .063 .071 .078 .085 .092 .100 .107 .114 .121 .128 .136 .143.006 .014 .021 .028 .035 .043 .050 .057 .064 .071 .079 .086 .093 .100 .107 .115 .122 .129 .136 .1440.20 0.21 0.22 0.23 200210220230.144.151.159.166.145.152.159.167.145.153.160.167.146.154.161.168.147.154.162.169.148.155.162.170.149.156.163.170.149.157.164.171.150.157.164.172.151.158.165.172W/S W 0 1 2 3 4 5 6 7 8 90.24 0.25 0.26 0.27 0.28 0.29 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42 0.43 0.44 0.45 0.46 0.47 240250260270280290300310320330340350360370380390400410420430440450460470.173.180.188.1953202.209.216.224.231.238.245.252.260.267.274.281.288.296.303.310.317.324.331.338.174.181.188.195.203.210.217.224.232.239.246.253.260.268.275.282.289.296.303.311.318.325.332.339.175.182.189.19.203.211.218.225.232.239.247.254.261.268.275.283.290.297.304.311.319.326.333.340.175.183.190.197.204.211.219.226.233.240.247.255.262.269.276.283.291.298.305.312.319.326.333.341.176.183.190.198.205.212.219.227.234.241.248.255.263.270.277.284.291.298.306.313.320.327.334.341.177.184.191.199.205.213.220.227.234.242.249.256.263.270.278.285.292.299.306.314.321.328.335.342.177.185.192.199.206.214.221.228.235.242.250.257.264.271.278.286.293.300.307.314.321.329.336.343.178.185.193.200.207.214.221.229.236.243.250.257.265.272.279.286.293.301.308.315.323.329.336.343.197.186.193.201.208.215.222.229.237.244.251.258.265.273.280.287.294.301.308.316.323.330.337.344.180.187.194.201.208.216.223.230.237.245.252.259.266.273.281.289.295.302.309.316.324.331.338.3450.48 0.49 0.50 480490500.346.353.360.346.353.360.347.354.361.348.355.362.348.355.363.349.356.363.350.357.364.351.358.365.351.358.365.352.3593.68W/S W 0 1 2 3 4 5 6 7 8 90.51 0.52 0.53 0.54 0.55 056 0.57 0.58 0.59 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70 0.71 0.72 0.73 0.74 510520530540550560570580590600610620630640650660670680690700710720730740.367.374.381.388.395.402.409.416.422.429.436.443.450.456.463.470.476.483.489.496.502.508.515.521.368.375.382.389.396.402.409.416.423.430.437.444.450.457.464.470.477.483.490.496.503.509.516.522.368.375.382.389.396.403.410.417.424.431.437.444.451.458.464.471.477.484.491.497.503.510.516.522.369.376.383.390.397.404.411.418.425.431.438.445.452.458.465.472.478.485.491.498.504.510.517.523.370.377.384.391.398.405.411.418.425.432.439.446.452.459.466.472.479.485.492.498.505.511.517.524.370.377.384.391.398.405.412.419.426.433.439.446.453.460.466.473.479.486.492.499.505.512.518524.371.378.385.392.399.406.413.420.427.433.440.447.454.460.467.474.480.487.493.500.506.512.519.525372.379.386.393.400.407.414.420.427.434.441448454461.468.474.481.488.494.500.507.513.519.525372.379.386.393.400.407.414.421.428.435.442.448.455.462.468.475.481.488.494.501.507.514.520.526.373.380.387.394.401.408.415.422.429.435.442.449.456.462.469.476.482.489.495.501.508.514.520.5270.75 0.76 0.77 750760770.527.533.540.528.534.540.529.535.541.529.535.541.530.536.542.530.537.543.531.537.543.532.538.544.532.538.544.533.539.545W/S W 0 1 2 3 4 5 6 7 8 90.78 0.79 0.80 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89 0.90 0.91 0.92 0.93 0.94 0.95 0.96 0.97 0.980.991.00 7807908008108208308408508608708808909009109209309409509609709809901000.546.552.558.564.569.575.581.587.592.598.603.609.614.619.625.630.635.640.645.650.655.660.665.546.552.558.564.570.576.581.587.593.598.604.609.615.620.625.630.636..641.646.651.656.660.547.553.559.565.571.576.582.588.593.599.604.610.615.621.626631.636.641.646.651.656.661.547.553.559.565.571.577.583.588.594.599.605.610.616.621.626.631.637.642.647.652.657.661.548.554.560.565.572.577.583.589.594.600.605.611.616.622.627.632.637.642.647.652.657.662..549.555.561.567.573.579.584590.596.601.607.612.617.623.628.633.638.643.648.653.658.663.549.555.561.567.573.579.584.590.596.601.607.612.617.623.628.633.638.643.648.653.658.663.550.556.562.568.573.579.585.591.596.602.607.613.618.623.628.634.639.644.649.654.658.663.550.556.562.568.574.580.585.591.597.602.608.613.618.624.629.634.639.644.649.654.658.664.551.557.563.569.575.580.586.592.597.603.608.614.619.624.629.635.640.645.650.655.659.664附录1B 样品厚度修正系数G （WS）样品厚度较厚：WS =0.01~3.49 见表W ：样品厚度（μm ）：S ：探针间距（mm ） W/S 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.090.00 0.10 0.20 0.30 0.400.50 0.60 0.70 0.80 0.901.00 1.10 1.20 1.30 1.401.50 1.600.0000 0.0721 0.1443 0.2164 0.28840.3597 0.4293 0.4957 0.5576 0.61410.6647 0.7093 0.7482 0.7817 0.81060.8352 0.85630.0072 0.0794 0.1515 0.2236 0.29560.3668 0.4361 0.5021 0.5635 0.61940.6694 0.7134 0.7518 0.7848 0.81320.8375 0.83820.0144 0.0866 0.1587 0.2308 0.30270.3738 0.4429 0.5085 0.5694 0.62470.6741 0.7175 0.7553 0.7879 0.81580.8397 0.86010.0216 0.0938 0.1659 0.2380 0.30990.3808 0.4496 0.5148 0.5751 0.62990.6787 0.7215 0.7589 0.7908 0.81840.8419 0.86200.0289 0.1010 0.1731 0.2452 0.31710.3878 0.4563 0.5210 0.5809 0.63510.6833 0.7255 0.7622 0.7938 0.82090.8441 0.86390.0361 0.1082 0.1803 0.2524 0.32420.3948 0.4630 0.5273 0.5866 0.64020.6877 0.7294 0.7666 0.7967 0.82340.8462 0.86570.0433 0.1154 0.1875 0.2596 0.33130.4018 0.4696 0.5334 0.5922 0.64520.6922 0.7333 0.7689 0.7996 0.82580.8483 0.86750.0505 0.1226 0.1948 0.2668 0.33850.4087 0.4762 0.5396 0.5978 0.65010.6965 0.7371 0.7122 0.8024 0.82820.8503 0.86920.0577 0.1298 0.2020 0.2740 0.34560.4156 0.4827 0.5456 0.6033 0.65510.7009 0.7408 0.7754 0.8052 0.83060.8524 0.87090.0649 0.1371 0.2092 0.2812 0.35260.4224 0.4892 0.5516 0.6087 0.65990.7051 0.7445 0.7786 0.8079 0.83290.8544 0.87261.70 1.80 1.90 0.87430.88970.90290.87600.89110.90410.87760.89250.90530.87920.89390.90640.88080.89520.90760.88230.89650.90870.88380.89780.90990.88530.89910.91100.88680.90040.91210.88830.90160.9131W/S 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.092.00 2.10 2.20 2.30 2.402.50 2.60 2.70 2.80 2.903.00 3.10 3.20 3.30 3.40 0.91420.92390.93230.93960.94590.95140.95620.96040.96410.96740.97030.97280.97510.97720.97900.91520.92480.93310.94020.94020.95190.95660.96080.96440.96770.97050.97310.97530.97740.97920.91620.92570.93380.94090.94700.95240.95710.96120.96480.96800.97080.97330.97560.97760.97940.91720.92660.93460.94150.94760.95290.95750.96160.96520.96830.97110.97360.97580.97780.97950.91820.92740.93530.94220.94820.95340.95790.96190.96550.96860.97130.97380.97600.97790.97970.91920.92830.93610.94280.94870.95380.95830.96230.96580.96890.97160.97400.97620.97810.97990.92020.92910.93680.94350.94930.95430.95880.96270.96610.96920.97180.97420.97640.97830.98000.92110.92990.93750.94410.94980.95480.95920.96300.96640.96940.97210.97450.97660.97850.98020.92210.93070.93820.94470.95030.95530.95960.96340.96670.96970.97240.97470.97680.97870.98030.92300.93150.93890.94530.95090.95570.96000.96370.96710.97000.97260.97490.97700.97880.9805如需所测值更精确，请查下表附录2样品形状和测量位置的修正系数D（d s）（1）圆形薄片直径d (mm)探针位置距圆心位置距边缘位置0mm 1/4 d 5 mm 4 mm 3 mm 2 mm20 23 25 27 30 32 35 38 40 42 45 50 55 57 60 63 65 0.97880.98390.98630.98820.99040.99160.99290.99400.99460.99510.99570.99650.99710.99730.99760.99780.99790.96330.97190.97610.97940.98320.98520.98760.98940.99040.99130.99240.99380.99190.99520.99570.99610.99630.96330.96620.96770.96880.97020.97090.97180.97250.97290.97330.97380.97440.97490.97510.97520.97550.97570.95080.95380.95530.95650.95800.95880.95980.96060.96100.96140.96200.96270.96330.96350.96380.96400.96410.92630.92950.93120.93250.93420.93510.93620.93710.93770.93820.94880.94970.94030.94060.94090.94120.94140.87020.87390.87580.87730.87930.88040.88170.88290.88350.88410.88490.88590.88680.88710.88750.88790.888170 75 80 90 100 0.99820.99850.99860.99890.99910.99680.99720.99760.99810.99840.97600.97620.97640.97680.97700.96450.96480.96500.96540.96570.94180.94210.94240.94290.94330.88860.88910.88950.89010.8904（2）矩形薄片正方形矩形d/s a/d=1 a/d=2 a/d=3 a/d≥41.0 0.2204 0.22051.25 0.2751 0.27021.5 0.3263 0.3286 0.32861.75 0.3794 0.3803 0.38032.0 0.4301 0.4297 0.42972.5 0.5192 0.5194 0.51943.0 0.5422 0.5957 0.5958 0.59584.0 0.6870 0.7115 0.7115 0.71155.0 0.7744 0.7887 0.7888 0.78887.5 0.8846 0.8905 0.8905 0.890510.0 0.9312 0.9345 0.9345 0.934515.0 0.9682 0.9696 0.9696 0.969620.0 0.9788 0.9830 0.9860 0.983040.0 0.9955 0.9957 0.9957 0.9957100 1.0000 1.0000 1.0000 1.0000d：短边长度a：长边长度s：探针间距提醒：每次开机启动，仪器会有一个自动校正和自动预热过程，初测试偶有5到10次测试数值不精确视为正常情况。