相对论动力学基础
- 格式:pdf
- 大小:816.72 KB
- 文档页数:8







理论力学动力学知识点总结理论力学动力学是物理学的一个重要分支,研究物体的运动与力的关系。
从牛顿的力学开始到现代相对论力学和量子力学,动力学一直在不断发展和完善。
动力学的核心是牛顿运动定律,它描述了物体受力时的运动规律。
以下是关于理论力学动力学的一些重要知识点总结。
1.牛顿第一定律牛顿第一定律也称为惯性定律,它描述了一个物体在没有外力作用下将保持匀速直线运动或保持静止的状态。
即物体有惯性,需要外力才能改变它的状态。
2.牛顿第二定律牛顿第二定律描述了物体受力时的加速度与作用力的关系。
根据牛顿第二定律可以得到F=ma的公式,其中F是作用力,m是物体的质量,a是物体的加速度。
牛顿第二定律也可以表示为力的矢量形式:F=dp/dt,其中p是物体的动量,t是时间。
3.牛顿第三定律牛顿第三定律也称为作用与反作用定律,它指出任何两个物体之间的相互作用力均有相等大小但方向相反的反作用力。
即作用力和反作用力是相互作用的两个力,它们的大小相等,方向相反。
4.动量动量是描述物体运动状态的物理量,定义为物体的质量乘以速度,表示为p=mv,其中p是动量,m是质量,v是速度。
根据牛顿第二定律可以得到动量定理:F=dp/dt,即力是动量随时间的变化率。
5.动能动能是描述物体运动能量的物理量,定义为物体的动量的平方与质量的乘积的一半,表示为K=(1/2)mv^2,其中K是动能,m是质量,v是速度。
动能定理描述了力对物体做功时动能的变化:W=ΔK,即功等于动能的变化。
6.势能势能是描述物体位置能量的物理量,表示为U。
重力势能是物体在重力场中的位置能量,定义为U=mgh,其中m是质量,g是重力加速度,h 是高度。
弹性势能是弹簧或弹性体储存的能量,定义为U=(1/2)kx^2,其中k是弹性系数,x是弹性体的变形量。
7.动能和势能的转换根据机械能守恒定律,当物体在没有外力做功的情况下,动能和势能可以互相转换,但总机械能保持不变。
例如,自由落体过程中,重力势能转化为动能,而摆动过程中,动能转化为重力势能。


物理学中的动力学理论动力学是物理学中一个重要的分支,其研究的是物体运动的规律和动力学定律。
在牛顿力学中,动力学被赋予了重要的地位,牛顿的三大定律正是动力学的基础。
而在现代物理学中,动力学依然占据着重要的地位,成为了现代科学和技术发展的重要基础。
一、牛顿动力学牛顿动力学是经典的动力学理论,是现代物理学的基础之一。
牛顿三大定律是牛顿动力学的重要内容,这三大定律描述了物体运动的基本规律。
牛顿第一定律:一个物体将保持原有的匀速直线运动状态,直到有外力作用使其改变状态。
牛顿第二定律:物体所受合力等于物体的质量乘以加速度。
牛顿第三定律:对于任何相互作用的物体,作用力总是相等而反向的。
即对于物体A对物体B施加了一个力,那么物体B对物体A也会施加一个大小相同,但方向相反的力。
基于这三大定律,牛顿动力学可以描述物体在不同的运动状态下所受到的力的作用,进而推导出物体的运动规律。
二、量子力学中的动力学理论量子力学是20世纪最重要的科学之一,是现代物理学的基础。
在量子力学中,动力学的研究对象是微观粒子的运动规律和动力学定律。
量子力学中的动力学理论受到波动力学的影响。
在波动力学中,粒子的行为可以被描述为波动函数,波动函数可以用薛定谔方程来描述。
在薛定谔方程中,波动函数的演化规律可以被描述为哈密顿量作用下的时间演化。
动力学定律在量子力学中同样适用,其中包括牛顿第二定律。
但是,由于量子力学中的粒子具有波粒二象性,因此动力学中的某些概念和原则需要重新考虑。
三、相对论中的动力学理论相对论是现代物理学的另一重要分支,主要研究物体在高速运动状态下的特性和运动规律。
在相对论中,动力学理论不再适用牛顿的三大定律,而是采用了爱因斯坦的相对论动力学。
相对论动力学基于爱因斯坦的质能关系式 E=mc²,当物体的速度接近光速时,其质量将增加,从而导致牛顿定律不再适用。
相对论动力学中的定律包括:守恒定律,质点运动规律和速度叠加原理等。
在相对论中,动力学定律的推导依赖于洛伦兹变换和洛伦兹因子等概念。

⼤学物理相对论复习资料狭义相对论基本内容⼀、狭义相对论的基本原理1. 迈克⽿逊实验迈克⽿逊莫雷实验的⽬的是测定地球相对以太的速度,实验结果:地球相对以太的速度为零,当时的物理理论不能解释该实验结果。
2. 爱因斯坦狭义相对论的基本假设相对性原理:物理学定律在所有的惯性系中形势都是相同的,即⼀切惯性系都是等价的。
光速不变原理:在所有的惯性系中,真空中(⾃由空间)光速具有相同的量值c 。
⼆、狭义相对论时空观1. 洛仑兹变换⼀个事件在惯性系S 中的时空坐标为(x, y, z, t),在沿x 轴以速度v 匀速运动的另⼀惯性系S '中的时空坐标为()x ,y ,z ,t ''''(0t t '==时刻两惯性系原点重合且相应轴重合),则该事件的时空坐标的变换关系称为洛仑兹变换:=-===-2'('''(x x vt y y z z v t t x c或?=+=??==+??2('''('x x vt y y z z v t t x c2. 同时是相对的两个事件在⼀个惯性系中同时同地发⽣,在⼀切惯性系中该两事件必同时同地发⽣;两个事件在⼀个惯性系中不同地点同时发⽣,在其它惯性系中该两事件不⼀定同时发⽣。
3. 时钟变慢(时间变缓)在⼀个惯性系中同⼀地点先后发⽣的两事件,在该惯性系静⽌的时钟测得的时间间隔为固有时间0τ,在另⼀相对该惯性系以速度v 匀速运动的时钟测得的时间间隔为t ?,两者的关系为?γττ==0t 。
4. 尺缩短(长度收缩)观测者与尺相对静⽌时测得尺长称固有长度0L ,观测者沿尺长⽅向以速度v 匀速运动时测得尺长为L ,两者关系为=L L 观察者垂直于尺长⽅向以速度v 匀速运动时测得尺长为L ',0L L '=。
5. 狭义相对论时空观与经典时空观的⽐较当v c 时在x ≯ct 的时空范围内洛仑兹变换转化为伽利略变换,经典时空观是上述条件下狭义相对论时空观的极限。
推导相对论动力学的基本公式相对论是现代物理学的重要分支之一,其基本理论是由爱因斯坦在20世纪初提出的。
相对论动力学是相对论的一个重要组成部分,研究物体在相对论条件下的运动规律。
本文将从牛顿力学出发,逐步推导相对论动力学的基本公式。
1. 牛顿力学的基本原理牛顿力学是经典物理学的基石,以牛顿三定律为基础。
第一定律指出物体在没有外力作用下保持匀速直线运动或静止;第二定律表明物体的加速度与作用力成正比,与物体质量成反比;第三定律指出任何两个物体之间都存在相互作用力,且大小相等、方向相反。
2. 光速不变原理相对论的核心概念之一是光速不变原理。
根据这一原理,光在任何惯性参考系中的速度都是不变的,即与观察者的运动状态无关。
这一原理的提出打破了牛顿力学中绝对时空观的桎梏,为相对论的发展奠定了基础。
3. 相对论速度叠加原理在推导相对论动力学的过程中,我们需要引入相对论速度叠加原理。
根据这一原理,两个相对运动的物体的速度不是简单地相加,而是通过洛伦兹变换来计算。
这是因为相对论中存在时空的扭曲效应,导致速度叠加规则与牛顿力学有所不同。
4. 相对论动量和能量的定义在相对论中,动量和能量也需要重新定义。
根据相对论动力学的推导,动量与速度之间的关系为p = mv/√(1 - v^2/c^2),其中m为物体的质量,v为物体的速度,c为光速。
相对论能量的定义为E = mc^2/√(1 - v^2/c^2),其中E为能量。
5. 相对论质能关系相对论动力学的一个重要结果是质能关系,即E = mc^2。
这个公式表明质量和能量之间存在等价关系,质量可以转化为能量,而能量也可以转化为质量。
这一公式在核能反应和粒子物理学中有着重要的应用。
6. 相对论动力学的运动方程根据相对论动力学的推导,物体在相对论条件下的运动方程为F = dp/dt,其中F为物体所受的力,p为物体的动量,t为时间。
这个运动方程与牛顿第二定律非常相似,但其中的动量和力的定义与牛顿力学有所不同。
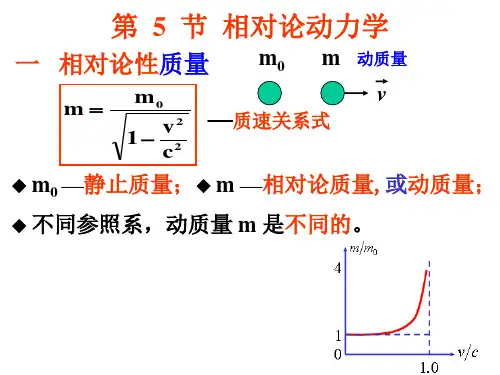
相对论相对论动力学的基本方程Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】第五十讲: § 相对论动力学基础一、 相对论质速关系式——揭示了质量和能量是不可分割的,这个公式建立了这两个属性在量值上的关系,它表示具有一定质量的物体客体也必具有和这质量相当的能量。
注意:自从质能关系发现以后,有些物理学家错误地解释了这个公式的本质。
他们把物质和质量混为一谈,把能量和物质分开,从而认为质量会转变为能量,也就表示物质会变成能量。
结果是物质消灭了,流下来的只是转化着的能量。
其实,这些论点是完全站不住脚的。
因为第一,质量仅仅是物质的属性之一,决不能把物质和它们的属性等同起来;第二, 质量和能量在量值上的联系,决不等同于这两个量可以相互转变。
事实上,在一切过程中,这两个量是分别守恒的,能量转化和守恒定律是一条普遍规律,质量守恒定律也是一条普遍规律,并没有发生什么能量向质量转变或质量向能量转变的情况。
举例:32年美国,加州理工学院对电子进行加速,c 999999.90=υ0900m m =⇒ ; 后对质子进行加速,0300m m =⇒☆相对论的动量:2201c m m P υ-==二、相对论动力学的基础方程⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-==2201c m dt d dt d υυ ()υυυdtdmdt d m m dt d +==c →υ ∞→m0→dtd υ这说明,无论使用多大的力,力持续的时间有多长,都不可能把物体加速≥光速。
只能是无限趋近。
三、相对论动能202E cm mc k -=当c υ 221E υm k =四、静能、总能和质能关系1、质能关系式;2mcE ∆=∆一千克物质折合成能量,一度电买一美分,值2500万美元; 一吨物质折合成能量,值250亿美元; 2、静能:物体静止的能量200c m E =3、总能:物体静止的能量和动能之和k E c m mc E +==202五、能量和动量的关系420222E cm c p +=习题1:某核电站年发电量为 100亿度,它等于36×1015 J的能量,如果这是由核材料的全部静止能转化产生的,则需要消耗的核材料的质量为 (A) √ kg. (B) kg.(C) (1/12)×107 kg. (D) 12×107kg.[]习题2:一个电子运动速度v = ,它的动能是:(电子的静止能量为 MeV) (A) . (B) MeV.(C) √ MeV. (D) MeV.[]习题3:狭义相对论中,一质点的质量m与速度v的关系式为______________;其动能的表达式为______________.答案:20)/(1c m m v -=2分202c m mc E K -= 2分习题4:质子在加速器中被加速,当其动能为静止能量的3倍时,其质量为静止质量的________倍.答案: 4 3分小结: 作业:P 预习:§。