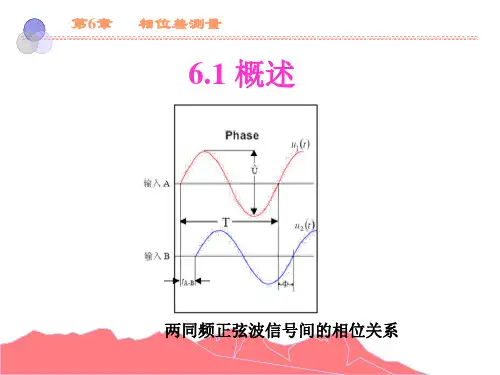
正弦信号相位测量
- 格式:docx
- 大小:33.41 KB
- 文档页数:2
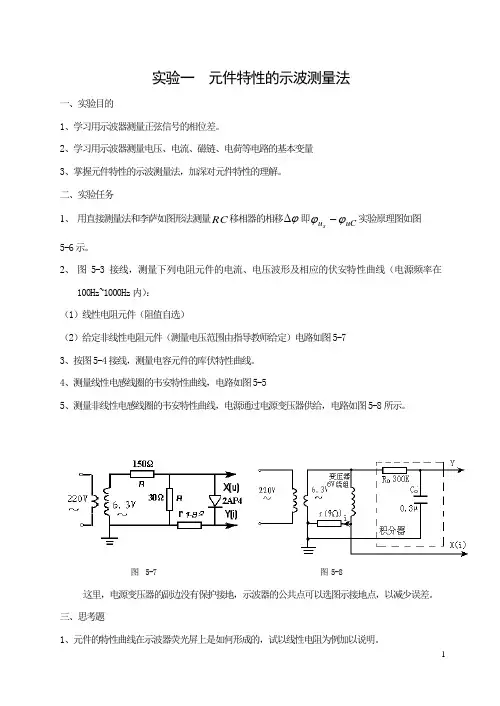
实验一 元件特性的示波测量法一、实验目的1、学习用示波器测量正弦信号的相位差。
2、学习用示波器测量电压、电流、磁链、电荷等电路的基本变量3、掌握元件特性的示波测量法,加深对元件特性的理解。
二、实验任务1、 用直接测量法和李萨如图形法测量RC 移相器的相移ϕ∆即uC u sϕϕ-实验原理图如图5-6示。
2、 图5-3接线,测量下列电阻元件的电流、电压波形及相应的伏安特性曲线(电源频率在100Hz~1000Hz 内): (1)线性电阻元件(阻值自选)(2)给定非线性电阻元件(测量电压范围由指导教师给定)电路如图5-7 3、按图5-4接线,测量电容元件的库伏特性曲线。
4、测量线性电感线圈的韦安特性曲线,电路如图5-55、测量非线性电感线圈的韦安特性曲线,电源通过电源变压器供给,电路如图5-8所示。
图 5-7 图 5-8这里,电源变压器的副边没有保护接地,示波器的公共点可以选图示接地点,以减少误差。
三、思考题1、元件的特性曲线在示波器荧光屏上是如何形成的,试以线性电阻为例加以说明。
答:利用示波器的X-Y方式,此时锯齿波信号被切断,X轴输入电阻的电流信号,经放大后加至水平偏转板。
Y轴输入电阻两端的电压信号经放大后加至垂直偏转板,荧屏上呈现的是u x,u Y的合成的图形。
即电流电压的伏安特性曲线。
3、为什么用示波器测量电路中电流要加取样电阻r,说明对r的阻值有何要求?答:因为示波器不识别电流信号,只识别电压信号。
所以要把电流信号转化为电压信号,而电阻上的电流、电压信号是同相的,只相差r倍。
r的阻值尽可能小,减少对电路的影响。
一般取1-9Ω。
四、实验结果1.电阻元件输入输出波形及伏安特性2.二极管元件输入输出波形及伏安特性实验二 基尔霍夫定律、叠加定理的验证 和线性有源一端口网络等效参数的测定一、实验目的1、加深对基尔霍夫定律、叠加定理和戴维南定理的内容和使用范围的理解。
2、学习线性有源一端口网络等效电路参数的测量方法3、学习自拟实验方案,合理设计电路和正确选用元件、设备、提高分析问题和解决问题的能力 二、实验原理 1、基尔霍夫定律:基尔霍夫定律是电路普遍适用的基本定律。

正弦波相位采样电路
正弦波相位采样电路是一种能够检测正弦波信号的相位信息的电路。
在采样过程中,通过将正弦波信号转换为相应的电平信号,并利用数字信号处理技术对采样数据进行处理,可以获得正弦波信号的相位信息。
下面是一个简单的正弦波相位采样电路的实现方案:
1.模拟-数字转换器(ADC):将正弦波信号转换为数字信号,用于后续的数字信号处理。
2.采样保持电路(S/H):用于在采样期间保持正弦波信号的幅度不变,以便于ADC进行准确的采样。
3.数字信号处理器(DSP):用于对ADC输出的数字信号进行处理,包括滤波、频谱分析和相位检测等。
4.相位检测算法:用于从数字信号中提取相位信息。
可以采用多种算法,如互相关法、自相关法、基于FFT的算法等。
在具体实现时,需要根据实际情况选择合适的ADC、DSP和相位检测算法,并设计合适的采样保持电路,以保证采样的准确性和可靠性。
此外,还需要注意采样频率、采样点数等参数的选择,以满足实际应用的需求。





基于LabVIEW 的正弦信号频率与相位测量1. 前言信号频率与相位的测量具有重要的实际意义。
本文调研了频率与相位的多种测量算法,并借助LabVIEW 编程实现。
在此基础上,对各种算法进行了比较研究,且提出了行之有效的改进措施。
2. 采样定理与误差分析2.1 采样定理时域信号()f t 的频谱若只占据有限频率区间m m ωω(-,),则信号可以用等间隔的采样值唯一表示,而最低采样频率为m 2f 。
采样定理表明:信号最大变化速度决定了信号所包含的最高频率分量,要使采样信号能够不失真地反映原信号,必须满足在最高频率分量的一个周期内至少采样两个点。
2.2 误差分析对连续周期信号()a x t 进行采样得离散序列()d x n ,如果满足采样定理,则离散序列()d x n 的傅里叶级数()dg X k 是连续信号()a x t 的傅里叶级数1()ag X k ω的周期延拓,否则会出现两种形式的误差。
2.2.1 泄漏误差在连续信号()a x t 一个周期1T 内采样1N 个点,如果正好满足11s N T T =(s T 为采样间隔),则是完整周期采样,采样结果()d x n 仍为周期序列,周期为1N 。
基于()d x n 一个周期1N 个点计算离散傅里叶级数()dg X k ,由()dg X k 可以准确得到连续信号()a x t 的傅里叶级数1()ag X k ω。
如果在连续信号()a x t 的M 个周期时间内采样整数1N 个点,即11s N T MT =,也是完整周期采样。
在此情况下,采样结果()d x n 仍为周期序列,周期为1N ,但()d x n 的一个周期对应于()a x t 的M 个周期,由离散序列()d x n 仍然可以准确得到连续信号()a x t 的频谱。
如果以上两种情况都不满足,则为不完整周期抽样,()d x n 也不再是周期序列。
如果取()d x n 近似周期的1N 个点计算傅立叶级数,则产生误差,此误差称为泄漏误差。

同频正弦信号间相位差测量的设计[导读]介绍了以单片机为核心,通过倍频电路实现的两同频正弦信号相位差测量的设计,并对该系统的硬、软件作了比较详尽的阐述。
关键词:信号介绍了以单片机为核心,通过倍频电路实现的两同频正弦信号相位差测量的设计,并对该系统的硬、软件作了比较详尽的阐述。
关键词:单片机,倍频电路,相位差1 引言本设计目的在于测量出任意两相同频率正弦信号之间的相位差,并将测量结果以数字形式显示出来。
具体实现方法为:先通过比较电路将两路同频信号分别转换为相应的脉冲信号,然后将其中的一路信号通过反相器取反后与另一路信号相与,得到一等脉宽的脉冲波形,此脉冲波形的脉宽t,即表示两信号的相位差。
将原信号对应的任意一路脉冲信号(周期为T)倍频后,作为单片机计数器的计数脉冲,并对相位差脉冲记数,得记数值为W。
设倍频电路的倍频系数为A,则记数脉冲周期为T/A,可得到两信号相位差角计算公式如下:其中N=360/A,N为常数,是相位测量系统的最小精确度。
经过单片机系统编程即可实现此简单运算式,并将运算结果Q送LED显示。
原理框图如图1所示。
2 系统硬件电路原理分析与设计整个系统硬件电路由比较整形电路、倍频电路、单片机AT89C51及显示电路组成。
2.1 比较整形电路电路采用电压比较器LM339。
LM339内有4个电压比较器,取其中的两个比较器即可。
两路信号分别接两个比较器同相输入端,将反相输入端接地,即构成过零比较电路。
两比较器输出即转换为脉冲信号。
将其中一路脉冲通过反相器CC4069取反后与另一路信号通过与门CC4081相与,可得一等脉宽的脉冲信号,此脉宽即记载着两输入信号之间的相位差,我们称之为相位差脉宽。
转换过程见图2。
2.2 倍频电路由相位差计算公式可知,倍频系数A越大,测量精度就越高,测量越准确。
本电路采用A=720的倍频电路,因此相位测量精度为N=360/720=0.5°,可以满足实际需要。
倍频电路由锁相环集成电路CC4046和双BCD(Binary-Coded DecimalNotation)同步加法计数器CC4518组成。

在电路测试实验中,相位差测量(简称相位测量)的应用很广泛。
例如测量各种滤波器移相器和放大器等双口网络的频率特性时,就需要对它们的输入信号与输出信号之间的相位差进行测量,也就是测量不同频率的正弦信号在通过双口网络时所产生的相位移。
用示波器来进行相位差的测量,能测量的最小相角可达5-10度。
双踪示波器测量相位差时,可采用直接显示波形的方法。
设有两个频率的正弦信号电压
U1=Vm1sin(ωt+φ1)
U2 =Vm2sin(ωt+φ2)
它们之间的相位差为Δφ=(ωt+φ1)-(ωt+φ2)=φ1-φ2 上式中φ1为电压U1的初相,φ2为电压U2的初相,由上式可知,两个同频率的正弦电压的相位差与时间无关。
将这两个被测的正弦信号分别输入到双踪示波器的CHA和CHB两通道内,如图C 所示,此时示波器X轴的线性锯齿波电压同时对两个被测信号进行扫描,调节两条扫描线(即时基线)使之重合,于是在示波器的荧光屏上就可以同时显示出两个信号的波形,如图 D所示。
根据荧光屏上显示的U1和U2两个信号的波形,量出它们的一个周期在示波器时间基线上所占的格数(所对应的相位为360度)和两个波形相位点在时间基线上间距的格数m,从而求得相位差
Δφ=(n/m)*360度
为了读数和计算方便,测量时可以适当调节示波器面板上的相关旋钮,使荧光屏上显示的信号的一个周期恰好为X轴上坐标刻度的九格(或八格),这样X轴上的刻度值每格就代表360度/9=40度(360度/8=45度)。

测试正弦波电信号的相位差时,
怎样正确选择公共参考点?
所谓相位差,是指同频率的两个正弦波信号初始角之间的角度差,因此,必须要有公共参考点,才能进行角度比较;而且,必须正确选择参考点,才能进行准确的相位测试。
例如,用数字相位计测量旋转变压器的输出相位差(也称相位移),应将旋转变压器的励磁绕组D1、D2和输绕组Z1、Z2的同名端D1、Z2挡在一起作为公共参考点(相位计参考输入与被测输入“地端”接通),励磁作为相位计参考信号,输出作为相位计被测信号,便可准确测出输出对励磁的相位差。
如果两者的异名端D2、Z1接在一起作为公共参考点,则测出的相位差将反180°。
如前者测出为7°,后者测出则为173°。
如果两者没有公共参考点(相位计两信号输入“地端”未接通),相位计将显示浮动的,不稳定的角度值,相位差无法测得。
检测正弦信号相位差算法的研究程捷(中国计量学院信息工程系, 杭州310034摘要本文基于最小二乘原理和FFT 的选频特性, 讨论了二种测量正弦信号相位差的方法。
该算法适用于短信号序列的相位测量。
实验结果表明这二种算法具有数据处理量少, 准确度高的特点。
关键词相位检测FFT 最小二乘法一、引言有直读法, 本文基于最小二乘原理和快速傅里叶变换(FFT 的选频特性, 提出了用最小二乘法和FFT 检测正弦信号相位差的算法。
影响算法的主要因素是采样点数。
利用最小二乘法数据处理量少, 准确度高, 而利用FFT 来检测相位差, 算法过程简捷。
二、算法的理论分析11最小二乘相位测量的算法假设有两正弦信号v 1(t 、v 2(t 被采样频率f s 采样, 得到一组M 个采样点。
待处理的信号如下式所示:v 1(t =V 1sin (Ξt +Υ1 v 2(t =V 2sin (Ξt +Υ2 (1展开上式可得v 1(t =C 0sin Ξt +C 1co s Ξt v 2(t =D 0sin Ξt +D 1co s Ξt (2其中: C 0=V 1co s Υ1, C 1=V 1sin Υ1D 0=V 2co s Υ2, D 1=V 2sin Υ2故有V1C 2+C 21, Υ1=arc tg C 0 +〔1-sgn (C 0 2V 2D 20+D 21,2tg D 0 2(3 , C j 、D j 参数(j =0,1 。
为此, 需要应用最小二乘法。
根据C j 、D j 参数总的测量残差平方和最小, 用求偏导数的方法得到C j 、D j 参数的最小二乘估计。
假设信号频率为f =50H z , 采样频率为f s , 选取一定量的采样数据(取决于周期数K 的值 , 则M =I N T (Kf s f =I N T (KN , 这里, I N T 表示取整。
采样间隔为∃=1 f s , 对连续的正弦信号按一定的时间间隔∃进行采样, 得到v i (n ∃ (i =1, 2, ; n =1, 2, …M 。
用光信号实现同步的相位测量方法
通过群体的光信号实现的同步的相位测量方法,具体可以分为以下几步:
1、两个节点点对点发射光信号,其中第一个节点发射出一个正弦波,第二个节点发射出的一个正弦波;
2、接收机1接收第一个节点发出的正弦波,接收机2接收第二节点发出的振动波;
3、第一个接收机将第一个节点发出的正弦波拉伸到与第二个节点发出的正弦波同样的时间跨度;
4、两个衰减的信号加权求和,计算两者之间的相位偏移;
5、基于计算出的相位偏移,使用选择性衰减技术来抵消相位偏移,调节光脉冲的宽度或者偏移角野;
6、将实现同步测量方法所需要的光信号分发给所有节点。
关于正弦信号相位测量
这次湖北省电子竞赛有一题是多功能计数器,要求测量10到100K的正弦信号的相位,我们的学生做了该题,方案是这样的
1、将两路同频率有相位差的正弦信号整形成方波;(用比较器或者施密特触发器)
2、两路信号二分频后异或得到高电平脉宽与相位(0到360度)成正比的PWM信号(不二分频只能测得0到180度);
3、用等精度测量原理计数测量高低电平时间比,计算相位,需要高稳定度的有源晶振,我们用的是66M的有源晶振,如果器件支持100M的,精度更高。
图中:
f0为高频基准时钟
fA为第一路相位差信号
fA为第二路相位差信号
start为微处理器启动停止测量控制信号
clr为微处理器启动前复位清零信号
state为反馈信号,让微处理器检测测量过程是否开始或结束
hq、lq为计数器,反映高低电平的时间比,处理器测得结果可计算出相位差。
相位差:0x3ec/(0x3ec+0x3e8)=0.5就是360*0.5=180度。