检测正弦信号相位差算法的研究(精)

文章标题：深度解析STM32计算两个正弦函数的相位差计算函数在现代电子领域，STM32芯片因其高性能、低功耗和丰富的外设资源而备受青睐。

在STM32的开发中，经常遇到需要计算两个正弦函数的相位差的情况，这对于很多实时控制系统和信号处理应用来说是至关重要的。

本文将深度分析STM32计算两个正弦函数的相位差计算函数的原理和实现方法，帮助读者更好地理解和应用这一函数。

1. 相位差计算函数的重要性在很多电子控制系统和通信系统中，需要计算两个正弦函数之间的相位差。

相位差是指两个正弦函数的波形图像在时间轴上的偏移量，它在信号处理、通信调制解调、数字滤波等领域都有着重要的应用。

在STM32的开发中，我们经常需要计算两路传感器信号或者通信信号的相位差，以实现精确的控制和通信。

2. 理论基础要计算两个正弦函数的相位差，需要用到信号处理中的相关知识，比如傅里叶变换、相位谱分析等。

在STM32的开发中，通常会采用离散时间傅里叶变换（DFT）来进行相位差的计算。

DFT可以将时域信号转换到频域，进而得到信号的幅度和相位信息。

对于两路正弦函数来说，我们可以先通过DFT得到它们的幅度和相位谱，然后计算相位谱的差值即可得到它们的相位差。

3. STM32中的相位差计算函数在STM32的标准库中，通常会提供相位差计算函数的库函数。

这些库函数通常基于DFT算法实现，能够高效地计算两个正弦函数的相位差。

在实际应用中，我们只需要调用这些库函数，传入两路正弦函数的数据，即可得到它们的相位差。

这极大地简化了相位差计算的复杂性，有效提升了开发效率。

4. 个人观点和总结通过本文的深度解析，相信读者对STM32计算两个正弦函数的相位差计算函数有了更深入的理解。

相位差计算函数在实际应用中扮演着重要的角色，它是实现精确控制和通信的关键。

我个人认为，在STM32开发中，我们更应该注重对相位差计算函数的细节理解和实际应用，才能更好地发挥其作用。

希望本文能为读者在STM32开发中的相位差计算提供一些借鉴和帮助。

stm32计算两个正弦函数的相位差计算函数摘要：一、引言二、stm32 介绍三、计算两个正弦函数的相位差原理四、stm32 实现相位差计算的方法五、实验结果与分析六、总结正文：一、引言在信号处理、通信系统中，计算两个正弦函数的相位差是一项重要的任务。

基于stm32 的嵌入式系统具有高性能、低功耗的特点，是实现该功能的理想平台。

本文将介绍如何使用stm32 计算两个正弦函数的相位差。

二、stm32 介绍STM32（意法半导体公司的一款基于ARM Cortex-M 内核的32 位微控制器）是一种广泛应用于嵌入式系统的芯片。

它具有高性能、低功耗、丰富的外设接口等特点，使得开发者能够方便地实现各种功能。

三、计算两个正弦函数的相位差原理在计算两个正弦函数的相位差时，通常采用以下原理：相位差= arcsin( (A * sin(ωt) - B * sin(ωt + φ)) / (A * cos(ωt) + B * cos(ωt + φ)))其中，A 和B 分别为两个正弦函数的振幅，ω为角频率，t 为时间，φ为相位差。

四、stm32 实现相位差计算的方法1.搭建stm32 开发环境，包括硬件、软件和调试工具。

2.配置stm32 的时钟、外设等资源。

3.使用ADC（模数转换器）采集正弦函数的模拟信号，并将其转换为数字信号。

4.使用定时器产生精确的时间基准，对数字信号进行采样。

5.在stm32 的内存中存储采样数据，进行相位差计算。

6.将计算结果通过串口、显示器等途径输出。

五、实验结果与分析通过实际实验，证实了基于stm32 的嵌入式系统能够正确计算两个正弦函数的相位差。

实验结果与理论预测相符，表明该方法具有一定的准确性和实用性。

六、总结本文介绍了如何使用stm32 计算两个正弦函数的相位差。

通过搭建stm32 开发环境，配置时钟、外设等资源，实现对正弦函数信号的采样、相位差计算及结果输出。

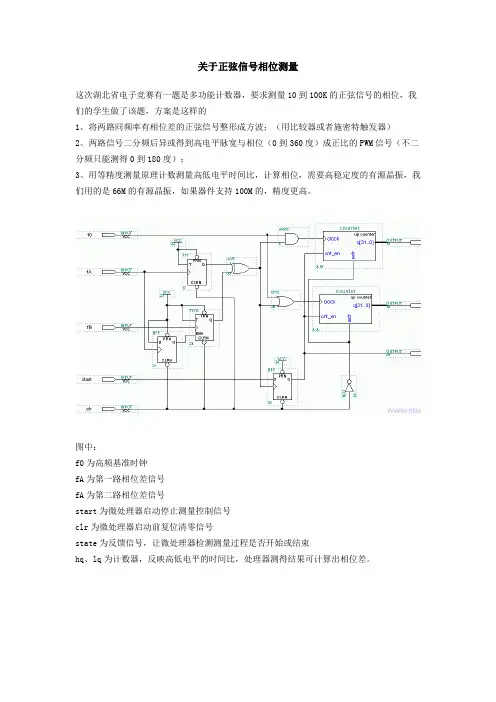
关于正弦信号相位测量
这次湖北省电子竞赛有一题是多功能计数器，要求测量10到100K的正弦信号的相位，我们的学生做了该题，方案是这样的
1、将两路同频率有相位差的正弦信号整形成方波；（用比较器或者施密特触发器）
2、两路信号二分频后异或得到高电平脉宽与相位（0到360度）成正比的PWM信号（不二分频只能测得0到180度）；
3、用等精度测量原理计数测量高低电平时间比，计算相位，需要高稳定度的有源晶振，我们用的是66M的有源晶振，如果器件支持100M的，精度更高。

图中：
f0为高频基准时钟
fA为第一路相位差信号
fA为第二路相位差信号
start为微处理器启动停止测量控制信号
clr为微处理器启动前复位清零信号
state为反馈信号，让微处理器检测测量过程是否开始或结束
hq、lq为计数器，反映高低电平的时间比，处理器测得结果可计算出相位差。

相位差：0x3ec/(0x3ec+0x3e8)=0.5就是360*0.5=180度。

同频正弦信号间相位差测量的设计[导读]介绍了以单片机为核心，通过倍频电路实现的两同频正弦信号相位差测量的设计，并对该系统的硬、软件作了比较详尽的阐述。

关键词：信号介绍了以单片机为核心，通过倍频电路实现的两同频正弦信号相位差测量的设计，并对该系统的硬、软件作了比较详尽的阐述。

关键词：单片机，倍频电路，相位差1 引言本设计目的在于测量出任意两相同频率正弦信号之间的相位差，并将测量结果以数字形式显示出来。

具体实现方法为：先通过比较电路将两路同频信号分别转换为相应的脉冲信号，然后将其中的一路信号通过反相器取反后与另一路信号相与，得到一等脉宽的脉冲波形，此脉冲波形的脉宽t，即表示两信号的相位差。

将原信号对应的任意一路脉冲信号（周期为T）倍频后，作为单片机计数器的计数脉冲，并对相位差脉冲记数，得记数值为W。

设倍频电路的倍频系数为A，则记数脉冲周期为T／A，可得到两信号相位差角计算公式如下：其中N＝360／A，N为常数，是相位测量系统的最小精确度。

经过单片机系统编程即可实现此简单运算式，并将运算结果Q送LED显示。

原理框图如图1所示。

2 系统硬件电路原理分析与设计整个系统硬件电路由比较整形电路、倍频电路、单片机AT89C51及显示电路组成。

2．1 比较整形电路电路采用电压比较器LM339。

LM339内有4个电压比较器，取其中的两个比较器即可。

两路信号分别接两个比较器同相输入端，将反相输入端接地，即构成过零比较电路。

两比较器输出即转换为脉冲信号。

将其中一路脉冲通过反相器CC4069取反后与另一路信号通过与门CC4081相与，可得一等脉宽的脉冲信号，此脉宽即记载着两输入信号之间的相位差，我们称之为相位差脉宽。

转换过程见图2。

2．2 倍频电路由相位差计算公式可知，倍频系数A越大，测量精度就越高，测量越准确。

本电路采用A＝720的倍频电路，因此相位测量精度为N＝360／720＝0．5°，可以满足实际需要。

倍频电路由锁相环集成电路CC4046和双BCD（Binary－Coded DecimalNotation）同步加法计数器CC4518组成。

测量相位差的实验方法标题：测量相位差的实验方法导言：相位差是物理学中一个重要的概念，它描述了两个波之间的时间差或相位延迟。

准确地测量相位差对于许多领域的研究与应用至关重要，如信号处理、光学、电子工程等。

本文将介绍一种实验方法来测量相位差，帮助读者更好地理解这一概念。

一、仪器准备1. 示波器：用于显示波形，测量波的幅度和相位。

2. 信号发生器：产生待测的两个信号。

3. 两个探头：用于将信号连接到示波器和信号发生器上。

二、实验步骤1. 连接示波器和信号发生器：(1) 将信号发生器的输出连接到示波器的通道一，用探头连接信号发生器和示波器。

(2) 将信号发生器的输出连接到示波器的通道二，用探头连接信号发生器和示波器。

2. 设置信号发生器：(1) 调节信号发生器的频率和振幅，使其适合实验需求。

(2) 分别设置两个信号发生器的相位差。

可以选择从0到360度的任意相位差。

3. 设置示波器：(1) 调节示波器的时间和电压刻度，使波形清晰可见。

(2) 将示波器设置为XY模式，以便观察相位差。

4. 观察示波器的显示：(1) 分别观察示波器的通道一和通道二的波形显示。

(2) 如果两个信号的相位差为0度，它们的波形将完全重合。

(3) 如果相位差不为0度，波形将出现相对位移。

5. 测量相位差：(1) 使用示波器的测量功能，测量两个波形之间的时间差或相位延迟。

(2) 示波器通常提供测量功能，如峰值差、周期差等。

(3) 根据实验需求选择合适的测量方法。

6. 记录测量结果：(1) 将测量得到的相位差记录下来。

(2) 可以尝试不同相位差下的测量，以获得更多数据。

三、实验结果与讨论1. 实验结果：(1) 在不同相位差下，测量得到的相位差值可以用图表或数据表格表示。

(2) 可以观察到相位差随着设置相位差的增加而改变。

2. 实验讨论：(1) 这个实验方法可以帮助我们直观地观察和测量相位差。

(2) 实验结果可以验证相位差的概念，并可用于进一步的研究和应用。

正弦信号的相频正弦信号的相频正弦信号是周期性的信号，可以用一个正弦函数来描述。

正弦信号的相频是指该信号波形相对于时间轴的相位变化速率。

下面将详细探讨正弦信号的相频。

一、正弦信号的基本概念正弦信号是一种周期性信号，是指在一定时间范围内，信号波形完全重复出现的现象。

正弦信号可以用如下的公式来表示：f(t) = A * sin(ωt+θ)其中，A表示振幅，ω为角频率，θ为相位。

当ω为定值时，f(t)就代表一种特定频率的正弦信号。

其波形特点为周期性、连续变化，显现出一定的振幅和相位特征。

二、相位和相频相位是指同一频率的正弦信号中，在任意时刻与某一参考时刻之间的时间差。

相频指的是，该信号波形相对于时间轴的相位变化速率。

相频值越大，则相位随时间的变化就越快，相频的单位一般为弧度/秒。

相频是描述正弦信号的重要指标之一，对于信号的处理、调制和识别都有着十分重要的意义。

在一些通信系统中，相频也被用来表达一些复杂信号的特征。

三、相频的计算方法1. 傅里叶变换法傅里叶变换方法可以将正弦信号转换为频域信号，从而求出相频。

具体方法是通过对信号进行傅里叶变换，将原信号从时域转换到频域。

然后在频域中进行相位差的计算，最终求出相频。

2. 相位差法相位差法最为简单易行，只需要通过对信号进行频域分析，求出两个信号的相位，然后计算其相位差，就能得到相频。

四、相频的应用正弦信号的相频在通信、电子等领域得到了广泛的应用。

通过正弦信号的相频，可以进行信号的调制、解调、信号分析等处理。

同时，对于一些特定类型的信号，如宽带调制信号等，其相位变化较为复杂，需要对其相位进行较为精细的分析和处理，以满足能够正确识别和提取转调信号的需求。

总之，正弦信号的相频是一项重要指标，对于信号处理、识别和分析都有着极为重要的意义。

随着技术的发展和应用场景的不断拓展，相频的应用也将得到更加广泛的开发和应用。

测量相位差的方法一、前言相位差是指两个波形之间的时间差，它在信号处理、通信系统、电路设计等领域中都有着广泛的应用。

测量相位差的方法也因此成为了一个重要的研究领域。

本文将介绍几种常见的测量相位差的方法及其原理。

二、比较法比较法是一种基于频率计算器和计数器的测量方法。

它通过将两个信号输入到频率计算器中，然后再将其输出到计数器中进行计数，最后通过比较两个信号的计数值来得到相位差。

具体步骤如下：1. 将待测信号和参考信号输入到频率计算器中，并设置好对应的频率范围。

2. 将频率计算器输出的脉冲信号输入到计数器中，并设置好对应的时间窗口。

3. 计算出待测信号和参考信号分别在时间窗口内产生了多少个脉冲。

4. 比较待测信号和参考信号产生脉冲数之间的差值，即可得到相位差。

三、插值法插值法是一种基于数字化信号处理技术的测量方法。

它通过将待测信号和参考信号进行数字化处理，并将其插值到同一采样率下，然后再通过计算两个信号之间的差值来得到相位差。

具体步骤如下：1. 将待测信号和参考信号进行采样，并将其转换为数字信号。

2. 对待测信号和参考信号进行插值处理，使它们在同一采样率下。

3. 计算出待测信号和参考信号在同一时间点上的数值差值。

4. 将数值差值转换为相位差，即可得到最终结果。

四、FFT法FFT法是一种基于傅里叶变换的测量方法。

它通过将待测信号和参考信号进行傅里叶变换，并将其转换为频域表示，然后再通过计算两个信号之间的相位角度来得到相位差。

具体步骤如下：1. 将待测信号和参考信号进行傅里叶变换，并将其转换为频域表示。

2. 计算出待测信号和参考信号在对应频率上的相位角度。

3. 将相位角度转换为时间上的相位差，即可得到最终结果。

五、小结以上三种方法都有各自的优缺点。

比较法的优点是简单易行，但精度受到频率计算器和计数器的限制；插值法的优点是精度高，但需要进行数字化信号处理；FFT法的优点是能够处理多个频率分量，但需要进行傅里叶变换。

正弦信号检测⏹幅度未知的正弦信号检测⏹幅度、相位未知的正弦信号检测⏹幅度、相位、频率未知的正弦信号检测⏹幅度、相位、频率、到达时间未知的正弦信号检测0:[][]H z n w n =10:[]cos(2)[]H z n A f n w n πφ=++0,1,...,1n N =-2[]~(0,)w n N σ高斯白噪声中确定性信号检测0[]cos(2)s n f n =π+φ2211000()[][][]cos(2)N N n n T z n s n z n f n --==⎛⎫⎛⎫==π+φ>γ⎪ ⎪⎝⎭⎝⎭∑∑z A 未知2211000()[][][]cos(2)N N n n T z n s n z n f n --==⎛⎫⎛⎫==π+φ>γ⎪ ⎪⎝⎭⎝⎭∑∑z ⊗[]z n 0cos(2)f n π+φ1N n -=∑()2()T z 1H H γ><H 0H 1未知幅度信号的正弦信号检测结构1002ˆ[]cos(2)N mln A z n f n N -==π+φ∑()()1212(/2)(/2)D F F P Q Q P dQ QP d--=-++024681012141618200.10.20.30.40.50.60.70.80.91pfa=0.1pfa=0.01pfa=0.001pfa=0.0001pfa=0.00001P d检测性能：221010log /2NA σ222/2d NA =σ0:[][]H z n w n =10:[]cos(2)[]H z n A f n w n πφ=++高斯白噪声中确定性信号检测0,1,...,1n N =-2[]~(0,)w n N σA ，φ未知且A>02212ˆˆˆml A =α+α21ˆˆarctan ˆml⎛⎫-αφ= ⎪α⎝⎭11002ˆ[]cos 2N n z n f n N -=α=π∑12002ˆ[]sin 2N n z n f n N -=α=π∑1cos A α=φ2sin A α=φ10ˆˆ(|,,)()(|)p A H p H φΛ=>ηz z z 22122ˆˆln ()()4N Λ=α+ασz ⊗[]z n 0cos 2f n π1N n -=∑()21N1H H γ><H 0H 1⊗0sin 2f nπ1N n -=∑∑++()21N未知幅度、相位正弦信号的正交形式检测22122ˆˆln ()()4N Λ=α+ασz 212212000414ˆˆ[]exp(2)()N n z n f n I f N NN -=α+α=-π=∑20()ln I f >ση=γ1H 周期图⊗0exp(2)j f n -π1N n -=∑21N10H H γ><H 0H 1[]z n 未知幅度、相位正弦信号的周期图形式检测0()I f检测性能：1101[]cos 2N n z n f nN-=ξ=π∑1201[]sin 2N n z n f nN-=ξ=π∑212200121()[]exp(2)N n I f z n f n N -==-π=ξ+ξ>γ∑201221(,),2cos ~2,,2sin 2N H N A N H N A ⎧σ⎪⎪ξ⎪⎛⎫⎡⎤⎡⎤φ=⎨ ⎪⎢⎥⎢⎥ξσ⎣⎦⎪ ⎪⎢⎥⎪ ⎪⎢⎥φ⎪ ⎪⎢⎥⎣⎦⎝⎭⎩0I ξI 为真为真{}220000222()2Pr ()|Pr |/2/2F I f P I f H H Q χγγ⎧⎫⎛⎫=>γ=>=⎨⎬ ⎪σσσ⎝⎭⎩⎭0.20.42=n 1=n 4=n 8=n 16=n 2χ2 4 6 8 10 12 14 1622()p χχ{}220000222()2Pr ()|Pr |/2/2F I f P I f H H Q χγγ⎧⎫⎛⎫=>γ=>=⎨⎬ ⎪σσσ⎝⎭⎩⎭{}22001122()()1Pr ()|Pr |2ln /2/2D F I f P I f H H Q P χλ⎛⎫γ⎧⎫=>γ=>=⎨⎬ ⎪σσ⎩⎭⎝⎭2222/2cos /2sin 2/2/2N A N A NA ⎛⎫⎛⎫φφλ=+= ⎪ ⎪ ⎪ ⎪σσσ⎝⎭⎝⎭2.幅度、相位未知的正弦信号检测22()12ln D F P Q P χλ⎛⎫= ⎪⎝⎭024681012141618200.10.20.30.40.50.60.70.80.91P Dpfa=0.1pfa=0.01pfa=0.001pfa=0.0001pfa=0.00001pfa=0.000001pfa=0.0000001221010log /2NA σP d说明：对于低虚警率，与未知幅度情况相比，能噪比损失小于1dB0:[][]H z n w n =10:[]cos(2)[]H z n A f n w n πφ=++高斯白噪声中确定性信号检测0,1,...,1n N =-2[]~(0,)w n N σA ，φ，f 0未知且A>00010100ˆˆˆˆˆ(|,,,)(|,,,)max (|)(|)f p A f H p A f H p H p H φφ>η⇒>ηz z z z 00max ()f I f >γ判决式：0max ()f I f >γ判决式：21001()[]exp(2)N n I f z n f n N-==-π∑⊗00exp(2),01/2j f n f -π<<1N n -=∑21N1H H γ><H 0H 1[]z n 未知幅度、相位、频率正弦信号检测0()I f 选择最大值22()/212ln D F N P Q P χλ⎛⎫-= ⎪⎝⎭0246810121416182000.10.20.30.40.50.60.70.80.91pfa=0.0001Known f0N1=256N2=512N3=1024P d 0.0001F P =222NA λ=σ221010log /2NA σ0:[][]H z n w n =100:[]cos[2()][]H z n A f n n w n πφ=-++高斯白噪声中确定性信号检测0,1,...,1n N =-2[]~(0,)w n N σA ，φ，f 0，n 0未知且A>0010ˆˆˆˆ(|,,,,)(|)p A f n H p H φ>ηz z 判决式：0000,max ()n n f I f >γ判决式：00021001()[]exp(2)n M n n n I f z n f n M+-==-π∑⊗000exp(2),01/20j f n f n N M-π<<≤≤-1N n -=∑21N10H H γ><H 0H 1[]z n 未知幅度、相位、频率、到达时间正弦信号检测00()n I f 选择最大值000,max ()n n f I f >γ短时周期图或谱图0.20.41002003004000510152025Frequency ，f0Sample num ，n0S p e c t r o g r a m I (n 0,f 0）00.10.20.30.40.550100150200250300350Frequency ，f0S a m p l e n u m ，n 0参数：A=1,M=128N=512,n 0=128f 0=0.25,φ=0σ2=0.5谱图举例检测性能：22()(/21)2ln D F N M M P Q P χλ⎛⎫- ⎪= ⎪ ⎪⎝⎭222MAλ=σ22()/212ln D F N P Q P χλ⎛⎫-= ⎪⎝⎭22()12ln D F P Q P χλ⎛⎫= ⎪⎝⎭()()1212(/2)(/2)D F F P Q Q P d Q QP d--=-++幅度未知：幅度、相位未知：幅度、相位、频率未知：小结：本讲以正弦信号检测为例，分析了幅度未知，幅度、相位未知，幅度、相位、频率未知以及幅度、相位、频率、到达时间未知四种情况下的检测器结构及检测性能。

检测正弦信号相位差算法的研究程捷(中国计量学院信息工程系, 杭州310034摘要本文基于最小二乘原理和FFT 的选频特性, 讨论了二种测量正弦信号相位差的方法。

该算法适用于短信号序列的相位测量。

实验结果表明这二种算法具有数据处理量少, 准确度高的特点。

关键词相位检测FFT 最小二乘法一、引言有直读法, 本文基于最小二乘原理和快速傅里叶变换(FFT 的选频特性, 提出了用最小二乘法和FFT 检测正弦信号相位差的算法。

影响算法的主要因素是采样点数。

利用最小二乘法数据处理量少, 准确度高, 而利用FFT 来检测相位差, 算法过程简捷。

二、算法的理论分析11最小二乘相位测量的算法假设有两正弦信号v 1(t 、v 2(t 被采样频率f s 采样, 得到一组M 个采样点。

待处理的信号如下式所示:v 1(t =V 1sin (Ξt +Υ1 v 2(t =V 2sin (Ξt +Υ2 (1展开上式可得v 1(t =C 0sin Ξt +C 1co s Ξt v 2(t =D 0sin Ξt +D 1co s Ξt (2其中: C 0=V 1co s Υ1, C 1=V 1sin Υ1D 0=V 2co s Υ2, D 1=V 2sin Υ2故有V1C 2+C 21, Υ1=arc tg C 0 +〔1-sgn (C 0 2V 2D 20+D 21,2tg D 0 2(3 , C j 、D j 参数(j =0,1 。

为此, 需要应用最小二乘法。

根据C j 、D j 参数总的测量残差平方和最小, 用求偏导数的方法得到C j 、D j 参数的最小二乘估计。

假设信号频率为f =50H z , 采样频率为f s , 选取一定量的采样数据(取决于周期数K 的值 , 则M =I N T (Kf s f =I N T (KN , 这里, I N T 表示取整。

采样间隔为∃=1 f s , 对连续的正弦信号按一定的时间间隔∃进行采样, 得到v i (n ∃ (i =1, 2, ; n =1, 2, …M 。

如何用李萨如图法测同频正弦信号的相位差
将一个正弦波电压加到荧光屏垂直偏转板，把另一个正弦波电压加到水平偏转板。

这样，在荧光屏上出现的图形为一个椭圆，由它能很容易求出两电压之间的相［位］差。

其原理如下：
设加在垂直偏转板上的电压为，加在水平偏转板上的电压为
，则两正弦电压间的相［位］差为φ。

当ωt＝0时，
，。

由此可求出U
x
在x轴上的截距
，式中M
x
为示波器的放大器在水平方向上的偏转灵敏度。

设水平方向的最大偏移为b则有b＝M
x U
x
因
故
从图4．38－4可见，两个交流电压的相[位]差，可以由它们形成的李萨如图形在x轴方向上的截距和最大位移之比求出。

同频率的两个交流电在荧光屏上的图形，由两电压的相[位]差确定，如图4．38－5所示。

如果两个交流电的最大值U
x 和U
y
相同，且示波器的放大器在水平与竖直方
向的偏转灵敏度相同，根据振动的合成规律很容易知道，当两电压的相[位]差φ＝0°或φ＝180°时，图形是一条与x轴夹角为45°或135°的直线；当φ＝90°或270°时，图形为一个圆。

若两电压的频率成整数倍，屏上可得到比较复杂的稳定图形。

若两电压的频率不成整数倍，屏上将出现复杂的变化图形，这种情况无法观测，我们就不讨论了。