基于次态卡诺图的J、K激励函数最小化方法及时序逻辑电路自启动解读
- 格式:doc
- 大小:27.00 KB
- 文档页数:12






环型计数器的自启动设计马敬敏【摘要】分析环形计数器的结构特征及状态转换过程,给出了在环形计数器闭合反馈环路任何一位的位置断开环路,在次态函数卡诺图上进行激励函数逻辑修改实现环形计数器自启动设计的技术,目的是探索环型计数器自启动设计的逻辑修改技术,改进了目前的在保持右移移位寄存器内部结构不变的基础上只求解第1位触发器的激励函数的局限性设计方法,结果是简化了环形计数器的设计过程,从而使环形计数器自启动设计方法具有普遍适用性。
%Analysis of ring counter in the structure characteristics and state conversion process, given the in ring counter closed feedback loop any a disconnect position loop. In the next state Karnaugh map of incentive logic function modification technology to achieve ring counter design of self-correction, It's aimed to explore the logic function modification of self-correction in ring counters improved the current while maintaining the right shift shift register the same internal structure based on only solving the 1 bit flip-flop excitation functions for the limitation of design method, gesign progress of ring counter is simplified,so that the ring counter design of self-correction;method has general applicability.【期刊名称】《电子设计工程》【年(卷),期】2016(024)023【总页数】3页(P177-179)【关键词】环形计数器;自启动;次态卡诺图;逻辑修改;激励函数【作者】马敬敏【作者单位】渤海大学实验管理中心,辽宁锦州 121000【正文语种】中文【中图分类】TN702环形计数器是存在大量冗余无效状态的移位寄存器型计数器,自启动设计问题一直受到人们的关注。


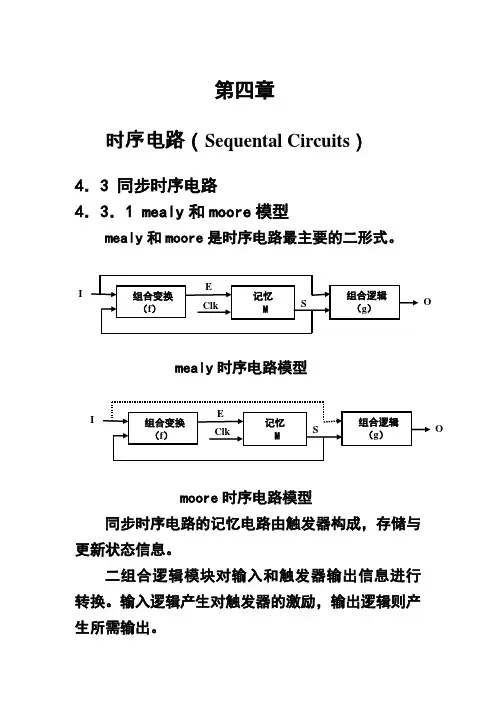
第四章时序电路(Sequental Circuits )4.3 同步时序电路4.3.1 mealy 和moore 模型mealy 和moore 是时序电路最主要的二形式。
mealy 时序电路模型moore 时序电路模型同步时序电路的记忆电路由触发器构成,存储与更新状态信息。
二组合逻辑模块对输入和触发器输出信息进行转换。
输入逻辑产生对触发器的激励,输出逻辑则产生所需输出。
OI OImealy 时序电路的输出是I 、S 的函数。
Moore 时序电路的输出仅是S 的函数。
4.3.2 时序电路的表述。
逻辑图,术语,状态图,符号状态表,代码状态表,激励表,激励方程,定时波形图。
时序电路状态机制中所用变量术语:输入变量:所有进入时序电路的外部变量。
输出变量:所有从时序电路发出的变量。
状态变量:触发器的输出,亦即时序电路的状态。
激励变量:触发器之输入。
因其“激励”触发器改变而得名。
激励变量就是触发器的J 、K 、R 、S 、D 、T 端,由输入组合逻辑对输入变量和状态变量逻辑运算产生。
状态变量是激励变量的函数。
状态:触发器的内容及输出。
时序电路的每个状态都必须是唯一的和不相互模糊。
时序电路的可能状态数 Y =2X (X :触发器数)。
时序电路的当前态(PS:Present state )、下态(NS: Next state)。
S t -1S tSt -1tClkt +1S t +1触发器所表示的时序电路状态只在时钟沿改变,所以以时钟沿分割状态。
现态(当前态)PS:在t时段的状态变量值。
下态(次态)NS:相对于t时段,时钟沿后t+1时段的状态值。
例:简单状态表。
时序电路状态图(state diagram)用抽象符号表示状态及其转换情况。
mealy型时序状态表示:例:X:输入变量。
Y:输出变量。
A、B:表示不同状态。
X/Z:表示输入/输出。
Moore 型时序状态表示:例:JK 触发器moore 型状态图表示。

数字电路中卡诺图的灵活应用刘玲【摘要】卡诺图是一种体现逻辑相邻关系的几何图形,多用于逻辑函数的表示和化简.通过实例,展示了卡诺图在求解逻辑函数的反函数、判断竞争冒险现象以及组合逻辑电路和时序逻辑电路设计中的应用.灵活运用卡诺图,将大大简化数字电路的分析和设计过程,起到事半功倍的效果.【期刊名称】《数字技术与应用》【年(卷),期】2016(000)005【总页数】2页(P51-52)【关键词】卡诺图;数字电路;逻辑函数;应用【作者】刘玲【作者单位】四川工商学院四川成都 611745【正文语种】中文【中图分类】TN79卡诺图是由2n个方格组成的、并能体现最小项逻辑相邻关系的几何图形。
从卡诺图上能直观地找出具有相邻关系的最小项并将其合并化简,这种方法无需特殊的技巧和熟记公式,只要按照正确的步骤和一定的化简原则就能容易地得到最简结果,因此卡诺图在逻辑函数化简中得以广泛的应用。
事实上,卡诺图除了可以化简逻辑函数,还有很多其他的用途,只要灵活运用,即可大大化简数字电路的分析和设计过程。
本文通过实例,阐述了卡诺图在逻辑函数化简之外的几点巧妙应用。
2.1 利用卡诺图求逻辑函数的反函数利用反演规则可以比较容易地求出逻辑函数的反函数,但得到的表达式并一定最简。
如果利用卡诺图,对逻辑函数表达式中没有出现的最小项之和进行化简,即采用包围0的方法,得到的表达式即为逻辑函数反函数的最简与或式。
例1:求逻辑函数的反函数。
解:画出逻辑函数的卡诺图(如图1),在卡诺图中对0加包围圈,可求出反函数的最简与或式,即得2.2 利用卡诺图分析组合逻辑电路中的竞争冒险在组合逻辑电路中,门电路的两个不同电平输入信号同时向相反方向转换的现象称为竞争,由竞争而可能产生输出干扰脉冲的现象称为冒险。
为保证电路正常工作,设计时需注意判断和消除竞争卡诺图法的步骤是:先画出逻辑函数的卡诺图,然后在卡诺图上画出与表达式中的乘积项相对应的包围圈,如果圈与圈之间出现相切,且相切处没有被其他圈包围,即可判断出现竞争冒险现象。

基于动态卡诺图的电路设计虞剑波(杭州师范大学信息工程学院,浙江杭州310018)应用科技日商要】在时序逻辑电路中,主要描述电路的工作状态,也就是触发器的状态转换,动态卡诺图就是为了适应这种工作状况从一般卡诺图引申出来的。
利用动态卡诺圈化简可以能够更简捷的求出触发器所需的数值,并且设计出更为简单的电路。
通过蕾文,能够更为详细的了解利用动态卡诺图设计时序逻辑电潞这一具体方法。
c关键词]逻辑函数;动态卡诺图;M A X pl usR1逻辑函数的卡诺图表示法1.1逻辑函数数字电路中,常常对逻辑函数进行化简。
那么什么是逻辑函数呢?如果以逻辑变量为输入,以运算结果为输出,那么当输入变量的取值确定之后,输出的取值便随之而定,因此,输出与输入之间是一种函数关系。
这种函数关系称为逻辑函数,写作Y=F(A,B,C,K)。
由于变最和输出(函数)的取值只有O和1两种状态,所以逻辑函数都是二值。
根据卡谱图的特性,逻辑函数可以由卡诺图进行表示。
12用卡诺图化简逻辑函数将n变量多的全部最小项各用一个小方块表示,并使具有逻辑相邻性的最小项在几l可_位置上也相邻地排列起来,所得到的图形叫做n变量最,J颂的卡诺图。
因为这种卡诺图是由美国工程师卡诺首先提出的,所以这种图形叫做卡诺图。
既然任何—个逻辑函数都能表示成若干最小项之和的形式,那么自然也就可以用卡诺图来表示任意—个逻辑函数。
具体方法是把逻辑函数化简成最,J、项之和的形式,然后在卡诺图上与这些最,J、项对应的位置上填入1,在其余的位置上填入0,就得到了表示该逻辑函数的卡诺图。
任何—个逻辑函数都等于它的卡诺图中填八1的那些最小项之和。
利用卡诺图化简逻辑函数的方法称为卡诺图化简法。
化简时的基本原理是合并具有相邻性的最,j、项,并消去不同的因子。
13合并最小项的规剧卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最,J颂,两个相邻最,J颂可以合并为一个与项并消去—个变量。
题2.4.18 试用负边沿JK 触发器和“与-或-非”门构成一个四位数码并行寄存和一个四位数码串行输入右移移位寄存器。
解:令C 是并行寄存数据和实现右向移位操作的控制端,其用JK 触发器构成的框图如图所示:令C=1并行存数,C=0时为右移串入后,得出各组合电路的逻辑函数,现以1J 3和1K 3函数为例,列出真值表,求出函数式,其它式子也照此类推。
输 入 输 出 C Q 2 D 3 1J 3 1K 30 0 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 0 1 1 1 11 0233311Q C CD K J +==122211Q C CD K J +==011111Q C CD K J +==SRD C CD K J +==00011由四个函数式画出的电路图如图所示:题2.4.19 图题2.4.19是一个实现串行加法的电路图,被加数11011及加数10111已分别存入二个五位被加数和加数移位寄存器中。
试分析并画出在六个时钟脉冲作用下全加器输出S i 端、进位触发器Q 端以及和数移位寄存器中左边第一位寄存单元的输出波形(要求时间一一对应)。
1D 2D 3DFF3 FF2 FF1 FF0 SR D 1J C1 1K 组合 逻辑电路 1JC1 1K 组合 逻辑电路1J C1 1K 组合 逻辑电路 1J C1 1K 组合 逻辑电路 CP0D0Q 1Q 2Q 3Q C D 1 D S1J QC11K11J Q C11K11J Q C11K11J Q C11K1CPC Q 3Q 2Q 1Q 0D 3 D 2 D 0≥1 &≥1 &≥1 &≥1 &图题2.4.19解:解该题时,注意全加器是一个合逻辑电路,而移位寄存器和触发器是一个时序电路,要注意时序关系。
其波形如图:题2.4.20 (1)试分析图题2.4.20(a)、(b)所示计数器的模是多少?采用什么编码进行计数?(2)若计数脉冲频率f CP 为700Hz 时,从Q 2端、Q 0端输出时的频率各为多少?图题2.4.20解:分析计数器电路有多种方法,列表法:以CP 为顺序,依次列出触发器的初态、输入,和次态,可以得出结论。
第四章例题解析【例1】电路如图4.15所示,试画出Q 1和Q 2的波形。
设两个触发器的初始状态均为“0”。
解答:对JK 触发器:J=Q 2,K=1,有nn n Q Q Q 1211=+ 对D 触发器: nn Q D Q Q D 1121,===+有有上述两方程画出Q 1和Q 2的波形图,如图4.16所示。
【例2】图4.17所示触发器电路中,A 和B 的波形已知,试对应画出Q 0~Q 3的波形。
设各触发器初态为0。
解答:①对图4.17(a )0010Q D Q n ==+,且在A 的上升沿翻转。
因0,110==Q Q R D 故时输出端被置为0。
n nn Q Q D Q 10111==+,且在B 的上升沿翻转。
②对图4.17(b )n n n n Q Q K Q J Q 222212=+=+,且在A 的下降沿翻转。
因为0332==Q Q R D ,所以时输出端被置为0。
n n n n n Q Q Q K Q J Q 3233313=+=+,且在B 的下降沿翻转。
Q 0、Q 1、Q 2、Q 3的波形如图4.18所示。
【例3】试画出主从结构RS 触发器转换成D 、T 、T ’及JK 型触发器的电路。
解答:RS 型触发器的特性方程为1=•+=+S R Q R S Q n n(1)RS →DD 触发器的特性方程为:n n n DQ D Q D D Q +=+==+)1(1 与RS 触发器的特性方程比较可得: S=D D R =根据方程式S=D ,D R =画出逻辑电路图,如图4.19所示。
(2)RS →TT 触发器的特性方程为:n n n Q T Q T Q+=+1与RS 触发器的特性方程比较可得:T R Q T S n==,但是当1,1==nQ T 时,出现R=1、S=1,不满足R ·S=0的约束条件。
故将T 触发器的特性方程变换为nn n n n n Q Q T Q T Q T Q T Q +=+=+1 与RS 触发器的特性方程联解可得:n n TQ R Q T S ==,根据方程式画出逻辑电路图,如图4.20所示。
基本RS触发器工作状态的Multisim仿真马敬敏【摘要】Muhisim simulation methods to basic RS flip-flop with set and reset functions and uncertain output states are given out. Word generator is used to generate all kinds of input signals, and four-trace oscilloscope is respond to display the input and output working waves. Thus the set and reset procedure and uncertain state production of flip-flop can be described directly. Then the logic expression of the uncertain state and Multisim simulation of basic RS flip-flop are analyzed. This method settles the question that the working waves of basic RS flip-flop are hard to be analyzed and verified by electronic devices.%给出了具有置0、置1功能及不确定输出状态的基本RS触发器的Multisim仿真方法,即用字组产生器产生所需的各类输入信号,用四踪示波器同步显示输入信号及状态输出信号的波形,可直观描述触发器的置O、置1过程及不确定状态的产生过程。
分析了基本RS触发器不确定状态的输出逻辑表达式及Muhisim仿真方案。
所述方法的创新点是解决了基本RS触发器的工作波形无法用电子实验仪器进行分析验证的问题。