数字逻辑基础卡诺图化简
- 格式:ppt
- 大小:1.96 MB
- 文档页数:54

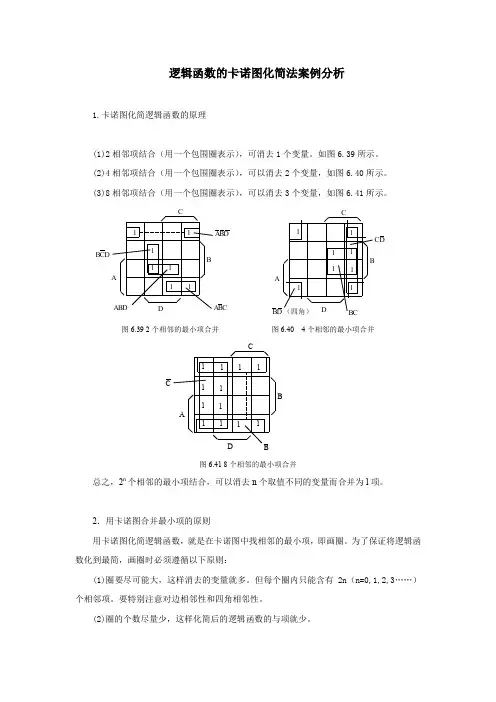
逻辑函数的卡诺图化简法案例分析1.卡诺图化简逻辑函数的原理(1)2相邻项结合(用一个包围圈表示),可消去1个变量。
如图6.39所示。
(2)4相邻项结合(用一个包围圈表示),可以消去2个变量,如图6.40所示。
(3)8相邻项结合(用一个包围圈表示),可以消去3个变量,如图6.41所示。
图6.39 2个相邻的最小项合并 图6.40 4个相邻的最小项合并图6.41 8个相邻的最小项合并总之,2n 个相邻的最小项结合,可以消去n 个取值不同的变量而合并为l 项。
2.用卡诺图合并最小项的原则用卡诺图化简逻辑函数,就是在卡诺图中找相邻的最小项,即画圈。
为了保证将逻辑函数化到最简,画圈时必须遵循以下原则:(1)圈要尽可能大,这样消去的变量就多。
但每个圈内只能含有2n (n=0,1,2,3……)个相邻项。
要特别注意对边相邻性和四角相邻性。
(2)圈的个数尽量少,这样化简后的逻辑函数的与项就少。
ABCDABC D111111111111111ABDABCABDBCDBC CDBD (四角)D ABC111111111111BC(3)卡诺图中所有取值为1的方格均要被圈过,即不能漏下取值为1的最小项。
(4)取值为1的方格可以被重复圈在不同的包围圈中,但在新画的包围圈中至少要含有1个末被圈过的1方格,否则该包围圈是多余的。
3.用卡诺图化简逻辑函数的步骤 (1)画出逻辑函数的卡诺图。
(2)合并相邻的最小项,即根据前述原则画圈。
(3)写出化简后的表达式。
每一个圈写一个最简与项,规则是,取值为l 的变量用原变量表示,取值为0的变量用反变量表示,将这些变量相与。
然后将所有与项进行逻辑加,即得最简与—或表达式。
例3:用卡诺图化简逻辑函数:D C B A D C B A D B A AD F +++= 解:(1)由表达式画出卡诺图如图6.43所示。
(2)画包围圈合并最小项,得简化的与—或表达式:D B AD F +=图6.42 例3卡诺图 图6.43例4卡诺图注意:图中的虚线圈是多余的,应去掉;图中的包围圈D B 是利用了四角相邻性。




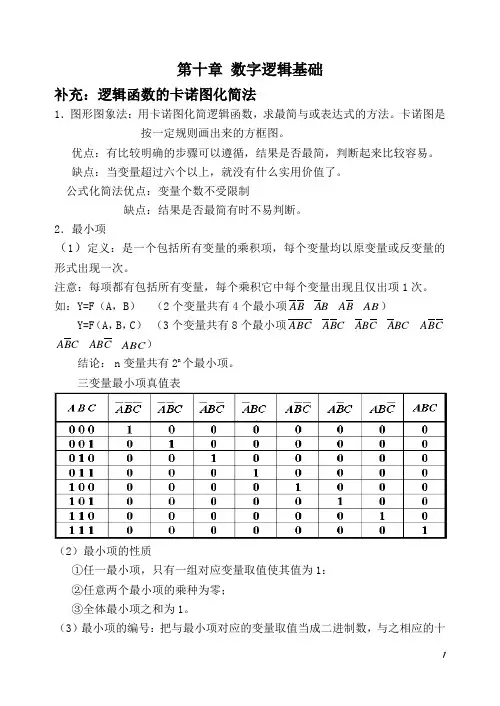
第十章 数字逻辑基础补充:逻辑函数的卡诺图化简法1.图形图象法:用卡诺图化简逻辑函数,求最简与或表达式的方法。
卡诺图是按一定规则画出来的方框图。
优点:有比较明确的步骤可以遵循,结果是否最简,判断起来比较容易。
缺点:当变量超过六个以上,就没有什么实用价值了。
公式化简法优点:变量个数不受限制缺点:结果是否最简有时不易判断。
2.最小项(1)定义:是一个包括所有变量的乘积项,每个变量均以原变量或反变量的形式出现一次。
注意:每项都有包括所有变量,每个乘积它中每个变量出现且仅出项1次。
如:Y=F (A ,B ) (2个变量共有4个最小项B A B A B A AB )Y=F (A ,B ,C ) (3个变量共有8个最小项C B A C B A C B A BC A C B AC B A C AB ABC )结论: n 变量共有2n 个最小项。
三变量最小项真值表(2)最小项的性质①任一最小项,只有一组对应变量取值使其值为1: ②任意两个最小项的乘种为零; ③全体最小项之和为1。
(3)最小项的编号:把与最小项对应的变量取值当成二进制数,与之相应的十进制数,就是该最小项的编号,用m i 表示。
3.最小项表达式——标准与或式任何逻辑函数都可以表示为最小项之和的形式——标准与或式。
而且这种形式是惟一的,即一个逻辑函数只有一种最小项表达式。
例1.写出下列函数的标准与或式:Y=F(A,B,C)=AB+BC+CA 解:Y=AB(C +C)+BC(A +A)+CA(B +B)=ABC C B A ABC BC A ABC C AB +++++ =ABC C B A BC A C AB +++ =3567m m m m +++例2.写出下列函数的标准与或式:C B AD AB Y ++=解:))()(C B D A B A Y +++=( ))((C B D B A ++= D C B C A B A B A +++=D C B A D C B A C B A C B A BC A ++++=D C B A D C B A D C B A D C B A D C B A D BC A BCD A ++++++=_ 8014567m m m m m m m ++++++= =)8,7,6,5,4,1,0(m ∑ 列真值表写最小项表达式。


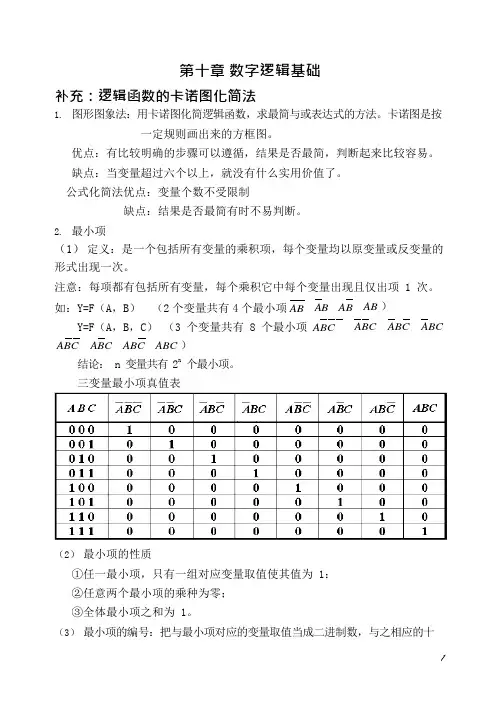
第十章数字逻辑基础补充:逻辑函数的卡诺图化简法1.图形图象法:用卡诺图化简逻辑函数,求最简与或表达式的方法。
卡诺图是按一定规则画出来的方框图。
优点:有比较明确的步骤可以遵循,结果是否最简,判断起来比较容易。
缺点:当变量超过六个以上,就没有什么实用价值了。
公式化简法优点:变量个数不受限制缺点:结果是否最简有时不易判断。
2.最小项(1)定义:是一个包括所有变量的乘积项,每个变量均以原变量或反变量的形式出现一次。
注意:每项都有包括所有变量,每个乘积它中每个变量出现且仅出项 1 次。
如:Y=F(A,B)(2 个变量共有4 个最小项AB AB AB AB )Y=F(A,B,C)(3 个变量共有 8 个最小项ABC ABC ABC ABC ABC ABC ABC ABC )结论: n 变量共有 2n个最小项。
三变量最小项真值表(2)最小项的性质①任一最小项,只有一组对应变量取值使其值为 1:②任意两个最小项的乘种为零;③全体最小项之和为 1。
(3)最小项的编号:把与最小项对应的变量取值当成二进制数,与之相应的十进制数,就是该最小项的编号,用 mi表示。
3.最小项表达式——标准与或式任何逻辑函数都可以表示为最小项之和的形式——标准与或式。
而且这种形式是惟一的,即一个逻辑函数只有一种最小项表达式。
例 1.写出下列函数的标准与或式:Y=F(A,B,C)=AB+BC+CA解:Y=AB( C +C)+BC( A +A)+CA( B +B)= ABC +ABC +ABC +ABC +ABC +ABC= ABC +ABC +ABC +ABC= m7 +m6+m5+m3例 2.写出下列函数的标准与或式:Y =AB +AD +BC解:Y =(A +B)( A +D)(B +C)= ( A +BD)(B +C)=AB +AB +AC +BCD=ABC +ABC +ABC +ABCD +ABCD=ABCD + _ ABCD +ABCD +ABCD +ABCD +ABCD +ABCD=m7 +m6+m5+m4+m1+m+m8=∑m(0,1,4,5,6,7,8)列真值表写最小项表达式。
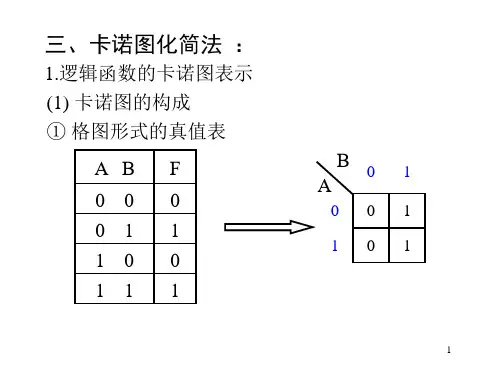
第二章 逻辑函数及逻辑门2-1 基本逻辑函数及运算规律 2-2 逻辑函数的真值表 2-3 逻辑函数的卡诺图卡诺图是逻辑函数的另一种表格化表示形式,它不但具有真值表的优点,还可以明确函数的最小项、最大项或任意项,并可一次性获得函数的最简表示式,所以卡诺图在逻辑函数的分析和设计中,得到了广泛的应用。
2-3-l 卡诺图的构成卡诺图是用直角坐标来划分一个逻辑平面,形成棋坪式方格,每个小方格就相当于输入变量的每一种组合。
小格中所填的逻辑值,即为对应输出函数值。
小格的编号就是输入变量按二进制权重的排序。
和真值表不同的是,坐标的划分应使变量在相邻小格间是按循环码排列的,因而便于函数在相邻最小项或最大项之间的吸收合并,能一目了然达到化简的目的。
二变量 卡诺图三变量 卡诺图四变量卡诺图例2-13 试画出函数Y=f (A,B,C,D)的卡诺图。
Y=∑m(0,1,2,8,11,13,14,15)+∑d(7,10)解按题中最小项及任意项的序号,分别在四变量卡诺图的对应小格内,填1或-,其余空格则填0,如图2-3所示。
由函数表达式填卡诺图例2-14试画出的卡诺图。
解:本题函数是四变量的积之和表达式,在填卡诺图之前,可先将它配项成最小项之和表达式:Y=∑m(2,5,8,10,12,14,15)同理,若已给函数是最大项之积表达式,则可按最大项序号在卡诺图对应格内填0,其余空格则填1。
若已给函数是和之积表达式,则可将函数配项成最大项之积形式,再按上述原则画卡诺图。
如果已知函数是既有积之和项,又有和之积项的混合形式,视方便可将它化成单一的积之和,或者是和之积形式,再进一步化成标准形式后,便可画成卡诺图。
例2-15 试画出函数Y的卡诺图。
Y=ПM(1,2,7)ΠD(3,6)解作三变量的卡诺图,如图2-5所示五变量卡诺图Y=AD+ABC+BCD+ABCD2-3-2用卡诺图化简函数 一、卡诺图化简原理 (1) 圈1法(最小项之和) ● 规则 ● 表达式例2-17 试用卡诺图化简函数Y =f (A ,B ,C)=∑m (0,2,4,7)。
数电逻辑表达式化简
数电逻辑表达式的化简是指将复杂的逻辑表达式简化为更简单的形式。
化简的目的是减少逻辑门的数量,简化电路结构,提高电路的可靠性和性能。
常用的逻辑表达式化简方法有两种:代数化简和卡诺图化简。
1. 代数化简:
- 使用布尔代数定律和布尔运算规则进行化简。
常用的代数
化简定律有:吸收定律、分配定律、德摩根定律等。
- 通过代数化简,将逻辑表达式中存在的冗余项、重复项、
冗长项等进行合并、简化,以达到减少逻辑门数量的目的。
2. 卡诺图化简:
- 将逻辑函数的真值表按照输入的组合方式进行分组,并绘
制成卡诺图。
- 通过对卡诺图的分析,找出逻辑函数中的主要项和次要项,去除冗余项,并将其化简为最简的逻辑表达式。
- 卡诺图化简方法适用于逻辑函数较复杂的情况,可以有效
地降低逻辑门的数量。
需要注意的是,在进行逻辑表达式化简时,要关注逻辑函数的功能需求,并根据具体的电路设计要求选择适合的化简方法。