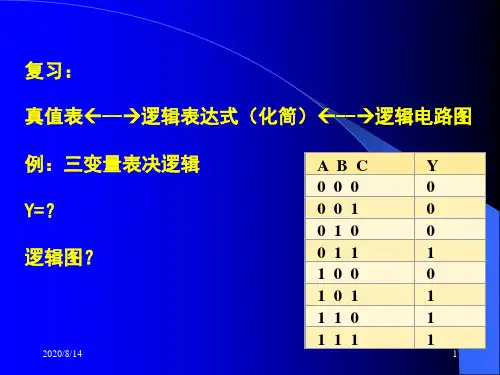
数字电路中的卡诺图

数字电路中的卡诺图――――――――――朱必成 F卡诺图是一幅或多幅方格子图形。

二至四变量卡诺图各占一幅图，五变量两幅，六变量四幅构成。

它贯穿了数字电路的各个层面，是十分重要且有用的基础知识。

经过课上学习与课外资料的查询，对其有了一定了解与认识。

1 化简的依据卡诺图具有循环邻接的特性，若图中两个相邻的方格均为1，则用两个相邻最小项的和表示可以消去一个变量，如4变量卡诺图中的方格5和方格7，它们的逻辑加是消取了变量C，即消去了相邻方格中不相同的那个因子。

若卡诺图中4个相邻的方格为1，则这4个相邻的最小项的和将消去两个变量，如4变量卡诺图中方格2、3、7、6，它们的逻辑加是消去了变量B和D,即消去相邻4个方格中不相同的那两个因子，这样反复应用A＋＝1的关系，就可使逻辑表达式得到简化。

这就是利用卡诺图法化简逻辑函数的基本原理。

2 用卡诺图化简逻辑函数的步骤1.将逻辑函数写成最小项表达式。

2.按最小项表达式填卡诺图，凡式中包含了的最小项，其对应方格填1，其余方格填0。

3.合并最小项，即将相邻的1方格圈成一组（包围圈，每一组含2n个方格），对应每个包围圈写成一个乘积项。

4.将所有包围圈所对应的乘积项相加。

有时也可以由真值表直接填卡诺图，1、2两步可以合成一步。

3画包围圈时应遵循的原则1.包围圈内的方格数必定是2n 个，n 等于0、1、2、3、…2.相邻方格包括上下底相邻，左右边相邻和四角相邻。

3.同一方格可以被不同的包围圈重复包围，但新增包围圈中一定要有新的1方格，否则该包围圈为多余。

4.包围圈内的1方格数要尽可能多，即包围圈应尽可能大。

4举例：5．卡诺图的应用技巧： （1）。

卡诺图中圈零：如 BD BC AD AC F +++=))((B A D C B A D C F F BA D C F ++=+==+= （2） 任意项的处理：实际中经常会遇到这样的问题，在真值表内对于变量的某些取值组合，函数的值可以是任意的，或者这些变量的取值根本不会出现，这些变量取值所对应的最小项称为无关项或任意项。

卡诺图在数字电路分析和设计中的应用数字电路分析和设计是电子技术中的一种重要技术，它主要是指分析和设计能够实现特定的功能的电路的过程。

在这一过程中，卡诺图被广泛地应用于电路的分析和设计中。

卡诺图（Karnaugh map）也称为猪头地图，它是一种用于分析模拟数字电路的有效方式，它是1952年由美国系统工程家萨姆卡诺（Samuel E. Karnaugh）提出的。

是用于组织可处理输入/输出表中的数字，其中引入条件把各种输入的值映射到输出的相应值，这些输入/输出表示某一个待解决的数字电路的性能。

Karnaugh map具有以下特点：它实现了快速的数字电路的分析，使系统设计者不必构建和分析整个电路，并可以有效地求得反射和置换门的最优组合。

在解决数字电路分析和设计时，卡诺图被广泛应用于电路的分析和设计中，因为它可以帮助系统设计者快速确定最优的逻辑组合，有效地实现目标功能，并能有效地节省设计时间。

随着技术的发展，系统设计者可以通过计算机软件和硬件来构建数字电路和分析卡诺图，从而实现迅速而准确地分析和设计数字电路。

除了用于数字电路分析和设计外，卡诺图还可以用于逻辑函数分析，控制系统分析等其他领域。

它为系统设计者带来了节省时间、提高效率和减少工程成本的优势，是一个强大的电路分析工具。

虽然卡诺图是一种有效的数字电路分析方法，但它仍有一些不足之处。

例如，当多个变量参与时，将需要复杂的计算，而且不同的逻辑置换和反射可能对应于不同的逻辑层次，这需要更多的工作。

此外，它也无法有效地处理复杂数字电路中的大量变量，而且也不利于复杂电路的分析和设计，这可能会影响系统设计的有效性。

因此，为了进一步提高卡诺图的有效性，已经有一些改进措施被提出，并已经得到了实现。

例如，可以在电路的分析和设计中使用复杂的数学算法，更进一步提高卡诺图的有效性。

综上所述，卡诺图是一种有效的方法，可以用于快速分析和设计数字电路。

它为系统设计者提供了节省时间、提高效率和减少工程成本的优势。

数字电路中卡诺图的灵活应用数字电路中的卡诺图是一种常用的逻辑化简工具，通过将真值表中的数据重新排列，从而找到可以优化的逻辑表达式，从而减少电路的复杂度，提高其性能和可靠性。

而卡诺图在实际应用中具备着很强的灵活性，下面我们来介绍一下它的一些常见应用。

一、最小化布尔函数卡诺图主要是用来最小化布尔函数的。

其基本思路是将真值表中的数据重新排列，从而找到可以优化的逻辑表达式。

因此，卡诺图在数码管、控制系统、DSP、单片机等各种数字电路中都有着非常广泛的应用。

通过卡诺图进行数字逻辑的设计，可以有效简化硬件设计，提高设计效率。

二、判断逻辑错误在数字电路中，逻辑错误很容易发生。

此时，可以通过卡诺图来检测逻辑错误。

通过重新排列真值表中的数据，可以清晰地分析逻辑关系是否正确。

这可以避免因为逻辑错误带来的电路故障等损失。

三、设计多输出函数在数字电路中，有很多复杂的多输出函数需要设计。

此时，可以通过卡诺图来进行设计。

将输入输出信号分别排列在卡诺图的行和列中，找出满足预期输出的函数。

这一技术可以帮助工程师设计出更加复杂的数字电路系统。

四、寻找未预料错误在数字电路中，未预料的错误总是存在的。

此时，可以通过卡诺图来寻找并解决这些错误。

通过重新排列真值表中的数据，可以发现其中的错误并进行解决。

这可以有效避免因为未预料的错误带来的电路故障等损失。

五、解决布线问题在数字电路中，布线问题也是非常重要的。

此时，可以通过卡诺图来解决布线问题。

通过重新排列真值表中的数据，可以找到电路中不必要的部分并进行简化，从而解决布线问题。

这可以极大地减轻电路布线的负担并提高电路的稳定性和可靠性。

在数字电路中，卡诺图具有很强的灵活性。

无论是在布线、逻辑设计、错误检测等方面，都可以通过它来解决问题。

同时，在实际的数字电路设计中，我们也可以对卡诺图进行适当的调整和改变，以改进设计方案并提高其性能。

数字电路中卡诺图的灵活应用
数字电路的设计离不开卡诺图，卡诺图是数字电路设计中非常重要的工具。

它可以用来精确地分析和优化逻辑电路，以减少电路的复杂度和节省成本。

在数字电路的设计过程中，卡诺图有着非常灵活的应用。

首先，卡诺图可以用来简化逻辑表达式。

在数字电路的设计中，一些逻辑表达式往往十分复杂，难以直接求解。

通过利用卡诺图可以将这些复杂的逻辑表达式转化为较简单的表达式，从而简化电路结构。

卡诺图的出现，让复杂的逻辑表达式变得清晰可见，方便电路设计者进行设计和优化。

其次，卡诺图可以用来优化布尔表达式。

布尔表达式和逻辑表达式在数字电路设计中的应用是非常广泛的。

但这些表达式往往十分复杂，需要进行化简和优化。

利用卡诺图可以很好的优化布尔表达式，让它们更加精简，降低电路的复杂度。

再来，卡诺图可以用来解决冗余逻辑的优化问题。

在数字电路的设计中，有时候我们会发现一些冗余的逻辑，这些逻辑在电路中没有意义，却增加了电路的复杂度。

利用卡诺图可以很好地排除冗余逻辑，从而达到优化电路结构的目的。

最后，卡诺图可以用来进行逻辑门电路的设计。

逻辑门电路是数字电路中最基本的设计单元，利用卡诺图可以方便地设计逻辑门电路，从而搭建出完整的数字电路系统。

总的来说，卡诺图在数字电路设计中有着非常灵活的应用，它
可以帮助设计者快速分析和优化逻辑电路，提高电路的可靠性和稳定性。

在实际应用过程中，设计者需要深入理解卡诺图的原理和应用，才能更好地利用卡诺图这一强大的工具。

数字电路中卡诺图的灵活应用刘玲【摘要】卡诺图是一种体现逻辑相邻关系的几何图形,多用于逻辑函数的表示和化简.通过实例,展示了卡诺图在求解逻辑函数的反函数、判断竞争冒险现象以及组合逻辑电路和时序逻辑电路设计中的应用.灵活运用卡诺图,将大大简化数字电路的分析和设计过程,起到事半功倍的效果.【期刊名称】《数字技术与应用》【年(卷),期】2016(000)005【总页数】2页(P51-52)【关键词】卡诺图;数字电路;逻辑函数;应用【作者】刘玲【作者单位】四川工商学院四川成都 611745【正文语种】中文【中图分类】TN79卡诺图是由2n个方格组成的、并能体现最小项逻辑相邻关系的几何图形。

从卡诺图上能直观地找出具有相邻关系的最小项并将其合并化简，这种方法无需特殊的技巧和熟记公式，只要按照正确的步骤和一定的化简原则就能容易地得到最简结果，因此卡诺图在逻辑函数化简中得以广泛的应用。

事实上，卡诺图除了可以化简逻辑函数，还有很多其他的用途，只要灵活运用，即可大大化简数字电路的分析和设计过程。

本文通过实例，阐述了卡诺图在逻辑函数化简之外的几点巧妙应用。

2.1 利用卡诺图求逻辑函数的反函数利用反演规则可以比较容易地求出逻辑函数的反函数，但得到的表达式并一定最简。

如果利用卡诺图，对逻辑函数表达式中没有出现的最小项之和进行化简，即采用包围0的方法，得到的表达式即为逻辑函数反函数的最简与或式。

例1：求逻辑函数的反函数。

解：画出逻辑函数的卡诺图（如图1），在卡诺图中对0加包围圈，可求出反函数的最简与或式，即得2.2 利用卡诺图分析组合逻辑电路中的竞争冒险在组合逻辑电路中，门电路的两个不同电平输入信号同时向相反方向转换的现象称为竞争，由竞争而可能产生输出干扰脉冲的现象称为冒险。

为保证电路正常工作，设计时需注意判断和消除竞争卡诺图法的步骤是：先画出逻辑函数的卡诺图，然后在卡诺图上画出与表达式中的乘积项相对应的包围圈，如果圈与圈之间出现相切，且相切处没有被其他圈包围，即可判断出现竞争冒险现象。

卡诺图在数字电路教学中的应用韩新风;高伟霞【摘要】卡诺图是逻辑电路中非常重要的分析工具,简单、直观、便于使用的特点使其在逻辑电路中有着广泛应用.现行的教材中虽然都介绍了相关的知识,但篇幅都不是很大,使得初学者不能系统地掌握卡诺图的应用.卡诺图不仅可以应用于逻辑函数的化简,还可以应用于逻辑函数表达式形式的变换、实现逻辑函数的运算、判断和消除逻辑电路的竞争冒险等.笔者通过具体实例,介绍了卡诺图在数字逻辑电路中的应用,体现了卡诺图的实用性.系统地掌握卡诺图的应用可以使学习者在学习过程中达到事半功倍的效果.%The Karnaugh map is a very important analysis tool of digital electronic circuit.Because of its unique simplicity and direct-viewing,it works easily and has been widely applied in the digital electronic circuit.In the current teaching material,it has been covered,but not enough to systematically grasp the applications of the Karnaugh map for beginners.The Karnagh map can be used not only to simplify the operation of logic functions,also to transform the expression type of the logic function.It can be applied not only to logic operation of two logic functions,also to judge and remove in the phenomenon of race and hazard of the combinational logic circuit.The writer systematically introduces the application of the Karnaugh map with examples.The learner will gain double pay in the learning process,if he systematically comprehends the application of the Karnagh map.【期刊名称】《重庆文理学院学报（自然科学版）》【年(卷),期】2011(030)006【总页数】4页(P74-77)【关键词】卡诺图;数字电路;逻辑函数;应用【作者】韩新风;高伟霞【作者单位】安徽科技学院理学院,安徽凤阳233100;安徽科技学院理学院,安徽凤阳233100【正文语种】中文【中图分类】TN791卡诺图是1953年美国贝尔实验室的电信工程师Maurice Karnaugh在维奇图的基础上提出的一种用于化简逻辑函数的方法.这种方法简单、直观、方便的特点使其在数字电路的分析和设计中得到了广泛的应用.由于在大多数的《数字电子技术》或《数字电路》的参考教材中，主要讲解卡诺图在逻辑函数化简中的应用［1-3］，从而导致初学者往往以为卡诺图只是数字电路分析和设计中用以化简逻辑函数的一种工具.其实不然.灵活地运用卡诺图，可以使逻辑电路的分析和设计过程大大地简化，让一些难题迎刃而解［4］.下面通过具体实例介绍卡诺图在数字电路分析中的几种应用.1 卡诺图在逻辑函数化简中的应用利用卡诺图化简逻辑函数，就是根据卡诺图合并的性质，将逻辑函数中包含最小项对应卡诺图中的小方格上的“1”，经过合并化简成最简与或式［5］.以下面的一个实例，作简要说明.例题1:化简逻辑函数Y=A'C+AC'+BC'+B'C.解:根据逻辑函数画出相应的卡诺图如图1(a)所示.根据卡诺图化简法的化简规则，将可能合并的最小项用线圈起来，存在多种合并方案.方案一如图1(b)所示，可得化简结果:Y=AB'+A'C+BC'.当然也可以按照方案二，如图1(c)所示，则得:Y=AB'+A'C+BC'.由此也可以看出:利用卡诺图化简逻辑函数式化简结果并不是唯一的.由于卡诺图在这方面的应用，相关参考教材中有着详细的讲述，在此笔者不再赘述. 图1 逻辑函数Y的卡诺图2 卡诺图在逻辑表达式形式变换中的应用逻辑函数可以用不同的形式表示，一般有“与或”、“与非-与非”、“与或非”、“或与”、“或非-或非”等5种形式.逻辑函数变换指的就是逻辑函数不同形式之间的变换.在以上5种形式中，“与或”式是最基本的形式.因为其它4种形式都可以很方便地变换成“与或”式，并且逻辑函数化简，一般是指将逻辑函数化成最简“与或”式.因此对其它形式向“与或”式的变换在此不予讨论，而要讨论如何将“与或”式变换成其它的形式［6］.2.1 利用卡诺图实现逻辑函数由“与或”式向“与非-与非”式的转换文献［1］说明可以利用摩根定理将与或表达式转换成与非-与非形式.同样也可以直接利用卡诺图写出与非-与非式.例题2:把逻辑函数F=AC+BC'写成与非-与非的最简形式.解:1)将逻辑函数F=AC+BC'的卡诺图画出如图2(a)所示.2)按照卡诺图法的化简规则把能够合并的最小项用线圈出，如图2(b)所示.3)写出逻辑函数F的与非-与非表达式.图2 逻辑函数F卡诺图书写规则:把每个圈所对应的因子(写成与项的形式)取其非变量后，做与非运算即可得到最简的与非-与非表示形式，则2.2 利用卡诺图实现逻辑函数由“与或”式向最简“与或非”式的转换在文献［1-3］中使用卡诺图化简逻辑函数，主要采用的是圈“1”法:即把可以合并的“1”用线圈起来，最后逻辑函数的表达式即为每个圈内对应因子的或运算.事实上，也可以采用圈“0”法:把卡诺图中可以合并的“0”用线圈起来，最后逻辑函数即为每个圈内对应因子的或非运算.下面通过例题3，对这种方法做具体说明. 例题3:把逻辑函数F=AC+BC'写成最简“与或非”式.解:1)逻辑函数F=AC+BC'的卡诺图表示如图2(a)所示.2)利用圈“0”法把能够合并“0”用线圈出，如图2(c)所示.3)写出逻辑函数F的最简与或非表达式.书写规则:把每个圈所对应的因子(写成与项的形式)，做或非运算即可得到最简的与或非表示形式，则2.3 利用卡诺图实现逻辑函数由“与或”式向最简“或与”式的转换要把逻辑函数的与或表达式写成最简“或与”式，依然采用圈“0”法，只不过每个圈内的因子用或运算形式表示，最后对所有因子做与运算.例题4:把逻辑函数F=AC+BC'写成最简“或与”式.解:1)逻辑函数F=AC+BC'卡诺图表示如图2(a)所示.2)利用圈“0”法把能够合并“0”用线圈出，如图2(c)所示.3)写出逻辑函数F的最简或与表达式.书写规则:①把每个圈所对应的因子，写成“或”项的形式.在写“或”项时，要将取值发生变化的变量消去，将不发生变化的变量保留，将1写作非变量，将0写作原变量.这同求“与或”式不同.②将第①步中写出所有“或”项做与运算即可得到逻辑函数的最简“或与”式. 逻辑函数F=AC+BC'的最简“或与”式:利用卡诺图实现逻辑函数形式的变换决不限于以上所述的几种.笔者只是通过以上几种变换说明卡诺图在逻辑函数形式变换中的应用.3 用卡诺图完成两逻辑函数的逻辑运算在逻辑函数的化简或运算中如果遇到较为复杂的情况时，可以借助于卡诺图来有效简化解决过程.例题5:已知逻辑函数把以下的逻辑函数化简为最简与或式:分析:这一类问题可以采用公式法，即把Y1和Y2代入待求的4个逻辑函数中，然后利用各类公式进行运算、化简.理论上可行，只是运算过程太过繁琐，极易出错.实际上，这类复杂的问题我们可以借助于卡诺图来解决.解:画出逻辑函数Y1和Y2的卡诺图，如图3(a)和图3(b)所示.图3 逻辑函数Y1和Y2的卡诺图1)对Y1和Y2的卡诺图中对应位置的两个小方格的“0”或“1”作与运算，把结果填到逻辑函数F1的卡诺图对应位置，即得如图4(a)所示的F1的卡诺图.然后利用其卡诺图对逻辑函数F1化简，如图4(b)所示.可得F1=Y1·Y2=CD+AB'D+A'B'C.图4 逻辑函数F1和F2的卡诺图2)对Y1和Y2的卡诺图中对应位置的两个小方格的“0”或“1”作或运算，把结果填到逻辑函数F2的卡诺图对应位置，即得如图5(c)所示的F2的卡诺图.然后利用其卡诺图对逻辑函数F2化简，如图4(d)所示.得F2=Y1+Y2=AB+C+B'D.由以上实例可以看出，可以利用卡诺图完成多种逻辑运算，除了以上实例中的与运算、或运算，还可以实现异或运算、同或运算.运算规则与以上类似:只要把两个逻辑函数卡诺图中对应位置的小方格内的逻辑变量做相应的运算即可.4 组合逻辑电路竞争冒险中的卡诺图任何一个门电路都具有一定的传输时间，当输入信号的状态突然改变时，输出信号不可能发生突变，需要滞后一段时间.这样，在信号的转换过程中，将会在门电路的输出端产生一个非正常的干扰脉冲.这种现象就是组合逻辑电路中的竞争冒险现象［7］.由于竞争冒险现象的存在，可能会导致输出结果的错误.利用卡诺图来判断和消除竞争冒险，就是一个比较有效快捷的方法.利用卡诺图可以判断是否存在竞争冒险:如果组合逻辑函数卡诺图中，合并项之间有相邻但不相交的项的情况，则说明设计的电路中存在竞争冒险.如图5(a)所示的卡诺图就存在这样的相邻项，其最简与或表达式为F3=AC+BC'.利用这种形式设计出的组合逻辑电路就会存在竞争冒险现象.利用卡诺图消除竞争冒险的方法:将卡诺图中相邻但不相交的项通过圈“1”的方式连接在一起，即通过增加冗余项来消除竞争冒险，如图5(b)所示.其或与表达式为:图5 逻辑函数F3的卡诺图5 结语卡诺图在数字电路的分析中有着广泛的应用.它的优点是简单、直观、使用方便，而且有一定的步骤和方法可循.在数字电路的教学中灵活应用卡诺图，可以让学习者在学习过程中达到事半功倍的效果.［参考文献］［1］阎石.数字电子技术基础［M］.北京:高等教育出版社，2006:42-57. ［2］康华光.电子技术基础:数字部分［M］.北京:高等教育出版社，2006:46-52. ［3］侯建军.数字电子技术基础［M］.北京:高等教育出版社，2007:29-35. ［4］王芳.基于数字电路中卡诺图的应用研究［J］.山西电子技术，2008(6):22-24.［5］王平均，吴恒玉.卡诺图在教学中的应用［J］.装备制造技术，2009(3):177-179.［6］王诗冰，黄正杰.关于卡诺图法实现逻辑函数变换的研究［J］.安徽职业技术学院学报，2005，4(1):5-8.［7］匡晚成，肖洪祥.卡诺图排列方法及在组合逻辑电路竞争冒险中的应用［J］.电子工程师，2007，33(6):48-50.。

使用卡诺图的技巧摘要：卡诺图是一种常用于简化逻辑表达式和优化电路的工具。

它通过比较不同的组合输入和输出值，帮助我们找到最小化逻辑电路所需要的最简化表达式。

本文将介绍一些使用卡诺图的技巧，包括如何使用它来快速找到最简逻辑表达式、使用简化的布尔代数来简化电路等内容。

关键词：卡诺图、逻辑表达式、电路、布尔代数、优化正文：卡诺图是一种非常有用的工具，尤其是在电路设计和逻辑优化的过程中。

它的本质原理是比较不同输入和输出组合，以此来确定最小化逻辑电路所需要的最简化表达式。

下面介绍一些利用卡诺图的技巧：1. 确定卡诺图大小当我们需要使用卡诺图来简化逻辑表达式时，首先需要确定卡诺图的大小。

卡诺图的大小通常取决于所涉及的变量的数量。

计算出变量的数量后，我们可以使用下表来确定卡诺图的大小：变量（数目） | 卡诺图大小--------------|-------------1 | 2x12 | 2x23 | 4x44 | 4x45 | 8x86 | 8x87 | 8x88 | 8x82. 组织卡诺图一旦我们知道了卡诺图的大小，接下来的步骤就是将逻辑表达式中的每个变量映射到卡诺图中的一个格子上。

这样做的时候，可以采用灵活的方法，比如按字典顺序排列或按变量重要性对格子进行排序。

3. 找到主项和独立项在卡诺图中找到主项或者独立项，是确定最简逻辑表达式所必需的步骤。

主项代表着其输入变量的组合可以覆盖整个逻辑表达式中的输出。

独立项表示在逻辑表达式中单独出现的变量，可以使用这些项来表示逻辑表达式中的重复项。

4. 简化布尔代数卡诺图可以帮助我们简化布尔代数。

布尔代数也是一种常用于逻辑电路的表达式，通常包括AND、OR和NOT这些运算符。

卡诺图可以将不同的逻辑表达式映射到一个单一的布尔表达式，并消除其中的冗余项。

总之，卡诺图是一种非常有用的工具。

通过使用它，我们可以快速找到最简逻辑表达式和优化电路，以及简化布尔代数表达式。

在电路设计和逻辑优化中，熟练掌握卡诺图的技巧将是一个非常有用的技能。

第二章 逻辑函数及逻辑门2-1 基本逻辑函数及运算规律 2-2 逻辑函数的真值表 2-3 逻辑函数的卡诺图卡诺图是逻辑函数的另一种表格化表示形式，它不但具有真值表的优点，还可以明确函数的最小项、最大项或任意项，并可一次性获得函数的最简表示式，所以卡诺图在逻辑函数的分析和设计中，得到了广泛的应用。

2-3-l 卡诺图的构成卡诺图是用直角坐标来划分一个逻辑平面，形成棋坪式方格，每个小方格就相当于输入变量的每一种组合。

小格中所填的逻辑值，即为对应输出函数值。

小格的编号就是输入变量按二进制权重的排序。

和真值表不同的是，坐标的划分应使变量在相邻小格间是按循环码排列的，因而便于函数在相邻最小项或最大项之间的吸收合并，能一目了然达到化简的目的。

二变量 卡诺图三变量 卡诺图四变量卡诺图例2-13 试画出函数Y＝f (A，B，C，D)的卡诺图。

Y＝∑m(0，1，2，8，11，13，14，15)+∑d(7，10)解按题中最小项及任意项的序号，分别在四变量卡诺图的对应小格内，填1或-，其余空格则填0，如图2-3所示。

由函数表达式填卡诺图例2-14试画出的卡诺图。

解：本题函数是四变量的积之和表达式，在填卡诺图之前，可先将它配项成最小项之和表达式：Y=∑m(2，5，8，10，12，14，15)同理，若已给函数是最大项之积表达式，则可按最大项序号在卡诺图对应格内填0，其余空格则填1。

若已给函数是和之积表达式，则可将函数配项成最大项之积形式，再按上述原则画卡诺图。

如果已知函数是既有积之和项，又有和之积项的混合形式，视方便可将它化成单一的积之和，或者是和之积形式，再进一步化成标准形式后，便可画成卡诺图。

例2-15 试画出函数Y的卡诺图。

Y＝ПM(1，2，7)ΠD(3，6)解作三变量的卡诺图，如图2-5所示五变量卡诺图Y＝AD+ABC+BCD+ABCD2-3-2用卡诺图化简函数 一、卡诺图化简原理 (1) 圈1法(最小项之和) ● 规则 ● 表达式例2-17 试用卡诺图化简函数Y ＝f (A ，B ，C)＝∑m (0，2，4，7)。

卡诺图构成卡诺图是一种平面方格阵列图，n个变量的卡诺图由2n个小方格构成。

卡诺图是真值表图形化的结果，n个变量函数的真值表是用2n行的纵列依次给出变量的2n种取值，每行的取值与一个最小项对应；而n个变量函数的卡诺图是用二维图形中2n个小方格的坐标值给出变量的2n种取值，每个小方格与一个最小项对应。

AA1(a) (b)图2-2 二变量卡诺图的构成图2-2为二变量卡诺图，它由4个方格组成。

图2.4(b)表明各个方格与这两变量的关系。

每一列和每一行上的0和1分别代表变量A和B的值。

类似，我们可以画出三、四、五变量的卡诺图，它们由2n（n=3，4，5）个方格构成，如图2-3所示。

为表示方便，图中小方格也可省略最小项符号m而只标明下标。

变量沿坐标轴方向按循环码的规律进行取值。

如图2-3(c)中，变量AB的取值依次是00-01-11-10，也可以依次取为10-11-01-00等等，但此时最小项与小方格的对应关系发生了变化，应该作出相应的调整。

五变量卡诺图可看作是由两个四变量卡诺图组成，而六变量的卡诺图可看作是由4个四变量卡诺图所组成，因为其比较复杂并且用得不多，所以不再给出。

A A11BAE DC C图2-3 三、四、五变量卡诺图的构成从以上各卡诺图我们可看出：卡诺图上变量的排列有一定的规律性。

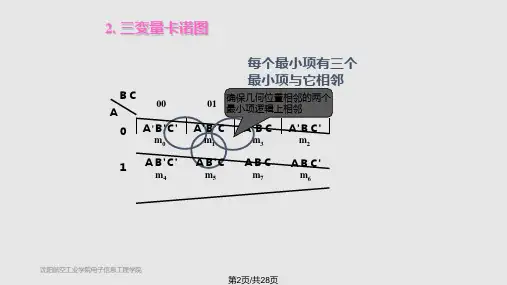
假定把彼此只有一个变量不同，且这个不同变量互为反变量的两个最小项称为相邻最小项，那么卡诺图上变量的排列规律将使最小项的相邻关系能在图形上清晰地反映出来。

根据此定义，我们可发现在卡诺图中只存在三种最小项间的相邻关系，即：1.几何相邻即几何位置上相邻的最小项，如四变量卡诺图中m0的相邻最小项m1和m4，这些最小项对应的小方格与m0对应的小方格分别相连。

1.相对相邻如四变量卡诺图中m0的相邻最小项中的m2和m8。

m0和m2处在同一列的两端，m0和m8处在同一行的两端，它们之间的位置都是“相对的”。

1.重叠相邻如五变量卡诺图中的m3与m1、m2、m7为几何相邻，与m11相对相邻，与m19则是重叠相邻。

物电11<11> 吴志峰 11415235卡诺图在数字电子技术中的数字逻辑电路设计的分析、化简中起着一个非常重要的数学工具的作用，通过系统的研究及总结可以让读者更为直观、全面的了解卡诺图并得以充分的利用。

1 卡诺图的定义卡诺图是逻辑函数的一种图形表示。

一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个方格图内，此方格图称为卡诺图。

卡诺图的构造特点使卡诺图具有一个重要性质：可以从图形上直观地找出相邻最小项。

两个相邻最小项可以合并为一个与项并消去一个变量。

2 用卡诺图表示逻辑函数2.1 最小项的意义N 个变量的最小项是n 个因子的乘积，每个变量都以它的原变量或非变量的形式在乘积项中出现，且仅出现一次。

任何一个逻辑函数经过逻辑代数的基本公式的变换，都能表示成唯一的若各干最小项之和的形式，即最小项表达式2.2 最小项的编号最小项通常用M i 表示，下标i 即最小项编号，用十进制表示。

将最小项中的原变量用1表示，非变量用0 表示，可得到最小项的编号以ABC 为例，因为它和000相对应，所以就称ABC 是和变量取值000相对应的最小项，而000相当于十进制中的0，所以把ABC 记作M 3。

2.3 卡诺图的引出卡诺图是逻辑函数的一种图形表示，是将此函数的最小项表达式中的各最小项相应地填入一个特定的方格内，特定方格的系统组成及内含规律即卡诺图的作图、算法的使用原则。

依据逻辑函数中变量数的不同，卡诺图也有相对应变量数图形，从简到繁依次为一变量卡诺图、二变量卡诺图、三变量卡诺图等。

下面给出常用的四变量卡诺图，其它图形可依此推演。

填入最小项的卡诺图 最小项简化表示法由此可得出卡诺图是可以直接观察相邻项。

也就是说，各小方格对应于各变量不同的组合，而且上下左右在集合上相邻的方格内只有一个因子有差别，这个重要特点成为卡诺图化简逻辑函数的主要依据。

现在以四变量卡诺图为例来说明，为清楚起见，把各最小项填入对应方格内，且用1表示原变量，0表示非变量。